Урок «Деформації. Механічні властивості твердих тіл. Модуль Юнга»

План-конспект уроку на тему:

«Деформації. Механічні властивості твердих тіл. Модуль Юнга»

Мета:

Навчальна: формувати поняття про «механічної напруги», «модуль Юнга», показати на практиці застосування знань про пружність, використовуючи закон Гука, розглянути діаграму розтягу твердих тіл.

Розвивальна: розвивати логічне мислення, вміння спостерігати фізичні явища; подальший розвиток вмінь учнів спостерігати, порівнювати, застосовувати раніше засвоєні знання в новій ситуації, міркувати, аналізувати, робити висновки.

Виховна: виховувати допитливість, увагу, бажання здобувати знання.

Тип уроку. комбінований урок.

Обладнання та наочність: план-конспект уроку, різні види деформації, прилад для демонстрації деформацій, портрети фізиків (Р.Гука, Т.Юнга).

План уроку:

1.Організаційний момент.

2. Перевірка домашнього завдання.

3. Мотивація навчальної діяльності.

4. Активізація опорних знань.

5. Вивчення нового матеріалу.

6. Закріплення нових знань та умінь.

7. Узагальнення вивченого матеріалу.

8. Оцінювання навчальних досягнень.

9. Домашнє завдання.

Хід уроку

1. Організаційна частина.

Привітання; перевірка присутніх; встановлення робочої атмосфери; пояснення виду робіт на уроці.

2. Перевірка домашньої завдання.

Щоб знайти ключове слово нашого уроку, розгадаємо з вами кросворд!

1. Прилад для вимірювання сили?

(динамометр)

2. Прилад для визначення маси тіла за діючою на нього силою тяжіння, а також назва сузір’я?

(терези)

3. Одиниця вимірювання сили.

(Ньютон)

4. Лінія, яку описує матеріальна точка, що рухається в простор.

(траєкторія)

5. Кисень, водень, азот, гелій це…..

(газ)

6. Явище незмінності швидкості руху матеріальної точки за відсутності зовнішніх сил. Явище , яке  відкрив італійський учений Галілео Галілей. На основі своїх дослідів і міркувань він стверджував: якщо на тіло не діють інші тіла, то воно або перебуває у спокої, або рухається прямолінійно і рівномірно.

(Інерція)

7. Фізична величина, що відповідає відношенню переміщення тіла до проміжку часу, за який це переміщення відбувалось. ЇЇ показують спідометри на автомобілях.

(швидкість)

					1
				2
	3
				4
				5
	6
7

Відповідь: деформація

Наталка Полтавка на початку відомого твору Івана Котляревського співає пісню: «Віють вітри, віють буйні, аж дерева гнуться…» У фізиці кажуть: дерева деформуються. Чим сильніше дме вітер, тим сильніше гнуться дерева. Коли вітер стихає, дерева набувають свого початкового положення — деформація зникає. Але якщо вітер надто сильний, то гілки дерев, а іноді навіть цілі дерева можуть зламатися.

Про те, що таке деформація, за яких умов вона виникає, які існують види деформації і коли тіла їх зазнають. Ось для цього сьогодні ми з вами ознайомимося з темою «Деформації. Механічні властивості твердих тіл. Модуль Юнга».

4. Активізація опорних знань.

У природніх умовах частинки кристала перебувають у стані рівноваги: сили притягання і відштовхування між ними однакові. Під дією зовнішніх сил частинки кристала зміщуються, унаслідок чого змінюється його форма і розміри, тобто виникає деформація.

Досліди 1. з поролоновою губкою і пластиліном ( 2 учні). Подійте на них з силою, а потім різко припиніть її дію.

Чи однаковий кінцевий результат?

У чому різниця?

Ймовірна відповідь:

На пластиліні – слід, поролон прийняв колишню форму.

Вчитель:

Багато тіл, що оточують нас, може деформуватися, тобто змінювати свою форму під зовнішньою дією.

Деформації, які повністю зникають після припинення дії зовнішніх сил, називаються пружними.

Властивість матеріалу відновлювати свою форму і розміри після припинення дії зовнішніх сил називають пружністю матеріалу. Якщо, замінити сталеву пластину свинцевою, то після припинення дії зовнішніх сил форма пластини не відновлюється: деформація твердого тіла повністю не зникає.

Пластична деформація – деформація, що зберігається після припинення дії зовнішньої сили.

Властивість матеріалу зберігати придбану під дією зовнішніх сил форму називають пластичністю.

Вчитель:

Як називаються деформації, яким піддаються троси підйомних кранів?

Ймовірна відповідь:

Розтягування.

5. Вивчення нового матеріалу.

Вчитель:

Пружні деформації твердих тіл різноманітні. За характером дії зовнішніх сил усі деформації діляться на 4 основні види: розтяг (стиск), зсув, кручення і згин.

 

Викладач:

Досліди 2. Затиснемо в лапці штатива гумовий стержень, посередині якого щільно насаджено металеву шайбу. До нижнього кінця стержня прикладемо силу. У результаті стержень розтягується вздовж своєї осі – його довжина збільшується, а поперечні розмірим скорочуються і раніше щільно надіта на стержень шайба легко зісковзує вниз.

Як змінюються відстані між частинками речовини при розтягуванні, стисненні?

Ймовірна відповідь:

При розтягуванні – збільшуються, при стисненні відстань зменшуються.

Вид деформації	Ознаки
Розтягу	збільшується відстань між молекулярними шарами.
Стиску	зменшується відстань між молекулярними шарами.
Кручення	поворот одних молекулярних шарів щодо інших.
Згину	одні молекулярні шари розтягуються, а інші стискаються або розтягуються, але менше перших.
Зсуву	одні шари молекул зсуваються щодо інших.

Лінійна деформація (деформація розтягування) – деформація, при якій відбувається зміна тільки одного лінійного розміру тіла.

Деформацію розтягу описують такі фізичні величини:
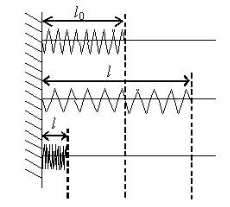
Абсолютне видовження:

де ∆l – абсолютне подовження (м); l і l₀ – кінцева і початкова довжина тіла (м).

Відносне видовження ε - відношення абсолютного видовження до початкової довжини тіла: , яке є безрозмірною величиною.

 

 

де ε – відносне подовження тіла;

∆l – абсолютне подовження тіла (м);

l₀ – початкова довжина тіла (м).

Відносне видовження показує значення абсолютного видовження, яке припадає на кожну одиницю початкової довжини тіла, що деформується.

Стан пружно деформованого тіла характеризують величиною σ, яка називається механічною напругою.

Механічна напруга σ дорівнює відношенню модуля сили пружності F_пр до площі поперечного перетину тіла S:

 

Вимірюється механічна напруга в Па.

Механічна напруга пружно деформованого тіла, залежить від матеріалу, з якого воно виготовлене, і значення відносного видовження. В однакових за розмірами тіл, але виготовлених з різних речовин, за одного й того самого відносного видовження виникає різна механічна напруга.

Механічну напругу, що виникає в речовині за відносного видовження називають модулем пружності k/

Зв'язок між силою пружності і пружною деформацією тіла (при малих деформаціях) був експериментально встановлений сучасником Ньютона англійським фізиком Робертом Гуком.

F_пр=kΔl

де k- модуль пружності,

Δl- абсолютне видовження.

k=E ,

де Е-коефіцієнт пропорційності, модуль пружності (модулем Юнга).

Модуль Юнга характеризує речовину з якої виготовлено стержня. На відміну від коефіцієнта пружності k , Е не залежить ні від довжини, ні від поперечного перерізу стержня.

Одиницею вимірювання Е Па.

Закон Гука можна записати формулою:

Спостереження показують, що при невеликих деформаціях механічна напруга у пропорційно відносному подовженні дорівнює:

Ця формула є одним з видів запису закону Гуку для одностороннього розтягування .

Чим більше модуль пружності Е, тим більша буде напруга σ тим менше деформується стержень за інших рівних умов (ℓ₀, S, F).

Якщо абсолютне видовження дорівнює початковій довжині Δl=l₀ (довжина тіла, що деформується, збільшується вдвічі), то з останнього співвідношення випливає, що Е=σ.

Таким чином, Модуль Юнга є такою механічною напругою, яка виникає в матеріалі під час збільшення початкової довжини тіла у 2 рази.

Закон Гука встановлює залежність між деформацією і механічною напругою аналітично. Але цю залежність можна виразити наочно у вигляді графіка – діаграми розтягу

Численні досліди показують, що при малих деформаціях напруга  прямопропорційно відносному подовженні (ділянка ОА діаграми) – виконується закон Гука.

Експеримент показує, що малі деформації повністю зникають після зняття навантаження (спостерігається пружна деформація). При малих деформаціях виконується закон Гука. Максимальна напруга, при якій ще виконується закон Гука, називається межею пропорційності ϭ_пп. Він відповідає точці А діаграми.

Якщо продовжувати збільшувати навантаження при розтягуванні і перевершити межу пропорційності, то деформація стає нелінійною (лінія ABCDF). Проте, при невеликих нелінійних деформаціях після зняття навантаження форма і розміри тіла практично відновлюються (ділянка АВ графіка). Максимальна напруга, при якій ще не виникають помітні залишкові деформації, називається межею пружності ϭ_пр. Він відповідає точці В діаграми. Межу пружності перевищує межа пропорційності не більше ніж на 0,33%. В більшості випадків їх можна вважати рівними.

Якщо зовнішнє навантаження таке, що в тілі виникає напруга, що перевищує межу пружності, то характер деформації міняється (ділянка BCDF). Після зняття навантаження зразок не приймає колишні розміри, а залишається деформованим, хоча і з меншим подовженням, чим при навантаженні (пластична деформація).

За межею пружності при деякому значенні напруги, відповідному точці діаграми, подовження зростає практично без збільшення навантаження (ділянка CD діаграми майже горизонтальна). Це явище називається текучістю матеріалу.

При подальшому збільшенні навантаження напруга підвищується (від точки D), після чого в найменш міцній частині зразка з'являється звуження («шийка»). Через зменшення площі перетину (точка F) для подальшого подовження потрібна менша напруга, але, врешті-решт, наступає руйнування зразка. Найбільша напруга, яка витримує зразок без руйнування, називається межею міцності. Позначимо його ϭ_м (воно відповідає точці F діаграми). Його значення сильно залежить від природи матеріалу і його обробки.

 

Механічна напруга	Позначення	Пояснення
Межа пропорційності	σпп	Максимальна напруга, при якій ще виконується закон Гука
Межа пружності	σпр	Максимальна напруга, при якій ще не виникають помітні залишкові деформації
Межа текучості	σт	Межа текучості
Межа міцності	σм	Найбільша напруга, яка витримує зразок без руйнування

 

Механічні властивості твердих тіл

Щоб споруджувати будинки, створювати надійні машини та механізми, виготовляти безпечні побутові прилади тощо, потрібно знати механічні властивості різноманітних матеріалів: бетону, металів, деревини, пластиків, скла.

Межа міцності багатьох матеріалів (мідь, цинк, залізо, незагартована сталь) значно більша за межу пружності. Такі матеріали мають достатньо широкі області пружних і пластичних деформацій, їх називають в’язкими матеріалами.

Проте разом з цим існує і цілий ряд матеріалів (чавун, скло, мармур, тощо), у яких межа міцності і межа пружності майже однакові. Такі матеріали називаються крихкими. У них область пластичних деформацій практично відсутня і руйнування наступає без появи залишкових практичних деформацій. Матеріали, у яких відсутня область пружних деформацій , називаються пластичними (віск, глина, пластилін тощо).

Поділ матеріалів на пружні й пластичні умовний, оскільки кожний матеріал здебільшого є одночасно і пластичним і пружним (приклад пружини). Крім того, властивості матеріалів великою мірою залежать від зовнішніх умов.

6. Закріплення нових знань та умінь, навичок.

Розв’язування задач.

1 В кінці XIX в. партію брюк, відправлених з Європи до Америки, упакували і склали в трюмі. Брюки злежалися так, що з'явилися «стрілки». Американці із захопленням сприйняли нову, як їм подумалося, європейську моду, яка потім розповсюдилася по всьому світу.

Що трапилося з тканиною брюк?  (Усно)

2. При розтягуванні алюмінієвої дротини завдовжки 2 м у ній виникла механічна напруга 35 МПа. Визначити відносне та абсолютне видовження.

3. Які сили треба прикласти до кінців стальної дротини, довжиною 4 м і з перерізом 0,5 мм², щоб видовжити її на 2 мм?

7. Узагальнення вивченого матеріалу.

Запитання до класу:

1. Що таке механічна деформація. Назвіть види деформацій.

2. Які фізичні величини описують деформацію розтягу чи стиску?

3. Що таке абсолютне видовження?

4. Що таке відносне видовження?

5. Що таке механічна напруга?

6. Сформулюйте закон Гука.

 

8. Оцінювання навчальних досягнень.

Вчитель підводить підсумки, виставляє оцінки та дякує учням за роботу на уроці.

9. Домашнє завдання.

 

 

Кросворд

4. Прилад для вимірювання сили?

(динамометр)

5. Прилад для визначення маси тіла за діючою на нього силою тяжіння, а також назва сузір’я?

(терези)

6. Одиниця вимірювання сили.

(Ньютон)

7. Лінія, яку описує матеріальна точка, що рухається в простор.

(траєкторія)

8. Кисень, водень, азот, гелій це…..

(газ)

9. Явище незмінності швидкості руху матеріальної точки за відсутності зовнішніх сил. Явище , яке  відкрив італійський учений Галілео Галілей. На основі своїх дослідів і міркувань він стверджував: якщо на тіло не діють інші тіла, то воно або перебуває у спокої, або рухається прямолінійно і рівномірно.

(інерція)

10. Фізична величина, що відповідає відношенню переміщення тіла до проміжку часу, за який це переміщення відбувалось. ЇЇ показують спідометри на автомобілях.

(швидкість)

					1
				2
	3
				4
				5
	6
7

 

Історична довідка

Роберт Гук (1635-1703), англійський фізик, математик, вчений, винахідник і архітектор, народився 1635 в містечку Фрешвотер в сім'ї настоятеля місцевої церкви.

У 1653 р. Гук вступив до Оксфордського університету. Один з викладачів університету порекомендував його Роберту Бойлю в якості асистента для проведення експериментальних досліджень. Співпраця Бойля і Гука була дуже плідною: його результатом стало створення удосконаленого повітряного насоса, застосування якого дозволило провести безліч цікавих дослідів.

У 1662 р. він отримав ступінь магістра мистецтв і в цьому ж році, завдяки допомозі Бойля, Гук був рекомендований на посаду демонстратора Лондонського королівського товариства.

Свою першу самостійну роботу, присвячену капілярності, Гук опублікував в 1661 р. Потім він займався дослідженнями в області астрономії.

Особливу популярність здобула праця Гука "Мікрографія", що вийшла друком в 1665 р. В ній викладені думки Гука і про природу світла, які дозволяють вважати його одним з основоположників хвильової теорії світла. Він прийшов до думки, що "світло являє собою досить короткі коливальні рухи, що відбуваються в поперечних напрямках до ліній поширення світла". Він пояснив походження інтерференційної забарвлення мильних бульбашок і явище ньютонових кілець.

У 1678 р. вийшла друком його робота про відновлювальну здатність чи про пружність. У ній містяться результати проведених Гуком дослідів з пружними тілами. Це була перша друкована праця, в якій розглядалися пружні властивості матеріалів. Роберт Гук не тільки встановив співвідношення між величиною сил і виробленими ними деформаціями, але і вказав ряд експериментів, де цим співвідношенням можна скористатися для вирішення деяких дуже важливих питань. Це лінійне співвідношення між силою і деформацією, відоме як закон Гука, і послужило фундаментом, на якому згодом отримала свій подальший розвиток механіка пружних тіл.

До кінця життя Р. Гук зробив близько 500 наукових і технічних відкриттів, включаючи закон пружності, конічний маятник, спиртовий рівень, морський барометр. Вони складають основу сучасної науки, але з різних причин приписуються іншим людям. У силу особливостей характеру і через надзвичайно широкого кола інтересів Гук часто не доводив свої відкриття до кінця і втрачав пріоритет, з приводу якого йому доводилося часто сперечатися з Ньютоном.

 

 

 

тОМАС ЮНГ

Старший з десяти дітей торговця шовком та оксамитом. Дуже рано навчився читати. У дитинстві виявив дивовижну здатність запам'ятовування різноманітних відомостей і текстів, допитливість і кмітливість. Володіючи різнобічними здібностями і інтересами,Юнг вже у вісім років займався геодезією і математикою. Підлітком знав латину, старогрецьку, давньоєврейську, італійську та французьку мови, вивчав арабську мову, а також історію і ботаніку. У 1792-1803 в Лондоні, Единбурзі, Геттінгені (у Геттінгенському університеті слухав лекції Г. К. Ліхтенберг), Кембриджі вивчав медицину. Потім займався оптикою і акустикою.

У 21 рік став членом Лондонського королівського товариства (1794), в 1802-1829 був його секретарем. У 1801-1803 був професором Королівського інституту в Лондоні.

У 1793 році в роботі «Спостереження над процесом зору» зазначив, що акомодація ока обумовлена зміною кривизни кришталика.

Оптичні спостереження привели Юнга до думки, що панувала в той час корпускулярна теорія світла невірна. Він висловився за хвильової теорії. Його ідеї викликали заперечення англійських учених; під їх впливом Юнг відмовився від своєї думки. Однак у трактаті з оптики і акустиці «Досліди і проблеми по звуку і світла» (1800) вчений знову прийшов до хвильової теорії світла і вперше розглянув проблему суперпозиції хвиль. Подальшим розвитком цієї проблеми стало відкриття Юнгом принципу інтерференції (сам термін був введений Юнгом в 1802 році).

У доповіді «Теорія  світла і кольорів», прочитане  Юнгом Королівському товариству в 1801 (опубліковано 1802), він дав пояснення кілець  Ньютона  на основі інтерференції і описав перші досліди з визначення довжин хвиль світла. У 1803 році в роботі «Досліди та обчислення пов'язані з фізичної оптики» (опублікована 1804) він розглянув явища дифракції. Після класичних досліджень О. Френеля з інтерференції поляризованого світла  Юнг  висловив гіпотезу про поперечності світлових коливань. Він розробив також теорію кольорового зору, засновану на припущенні про існування у сітчастій оболонці ока трьох родів чутливих волокон, що реагують на три основні кольори.

У 1807 році в двотомному праці «Курс  лекцій з натуральної філософії і механічному мистецтву» Юнг  узагальнив результати своїх теоретичних та експериментальних робіт з фізичної оптики (термін ввів Юнг) і виклав свої дослідження з деформації зсуву, ввів числову характеристику пружності при розтягуванні і стисненні - так званий модуль Юнга. Він вперше розглянув механічну роботу як величину, пропорційну енергії (термін ввів Юнг), під якою розумів величину, пропорційну масі і квадрату швидкості тіла.