Урок для 5 класу за темою:"Віднімання дробу від натурального числа"

Розробка уроку з математики для 5 класу з використанням новітніх технологій

за темою «Віднімання дробу від натурального числа».

Підготувала вчитель математики Волигіна Тетяна Михайлівна

 

 

Тема уроку: Віднімання дробу від натурального числа

 

Цілі уроку:

• Освітні: повторити правила додавання і віднімання дробів з однаковими знаменниками; навчити застосовувати їх при вирішенні завдань і знаходженні значень виразів; сформулювати правило віднімання дробу з натурального числа.

• Розвиваючі: розвивати пам'ять, логічне мислення, вміння формулювати проблему і знаходити її рішення.

• Виховні: виховувати самостійність, повагу до думки інших.

 

Тип уроку: комбінований.

 

Структура уроку:

1. Організаційний момент (1 хв.)

2. Актуалізація опорних знань. (7 хв.)

3. Гімнастика для очей. (1 хв.)

4. Перевірка знань за допомогою Kahoot! (4 хв.)

5. Повідомлення теми і мети уроку. (2 хв.)

6. Вивчення нового матеріалу. (14 хв.)

7. Фізкультхвилинка. (1 хв.)

8. Застосування отриманих знань при вирішенні задач.

• Тренувальні вправи. (4 хв.)
• Самостійна робота. (9 хв.)
• Складання фігур з конструктором Lego.

9. Домашнє завдання. (1 хв.)

10. Підсумок уроку. (1 хв.)

Обладнання: презентація, інтерактивна дошка, мобільні телефони, конструктор Lego, підручник Математика 5 клас, автори Н.А.Тарасенкова, І.М. Богатирьова, О.П.Бочко, О.М.Коломієць, З.О.Сердюк.

 

 

Хід уроку

1. Організаційний момент.

Сьогодні у нас незвичайний урок до нас в гості прийшли герої мультфільму "Смішарики" з конструктором Lego.

Протягом уроку за правильну відповідь ви кладете до себе у кошик по одній деталі конструктора Lego, а наприкінці уроку в парах збудуєте зі своїх деталей споруди.

Давайте відкриємо зошити, напишемо число і тему уроку.

 

2. Актуалізація опорних знань.

Як завжди урок ми почнемо з повторення.

Каждый может за версту
Видеть дробную черту.
Над чертой – числитель, знайте,
Под чертою – знаменатель.
Дробь такую, непременно, 
Надо звать обыкновенной

Число, яке показує, на скільки рівних частин розділили ціле, називається знаменник.

Число, яке показує, скільки рівних частин взято, називається чисельник.

1) Яка частина фігури замальована?

 

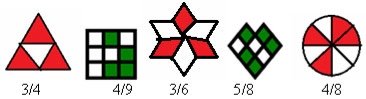
2) Розташуйте дроби в порядку зростання: 

Задача 1.

У городі у Копатича 10 грядок з овочами. грядок засаджено капустою. Скільки грядок на городі у Копатича з капустою? (Відповідь: 4 шт.)

 

Задача 2.

Їжачок збирає фантики. Нюша подарувала йому 34 штуки, Крош на 8 штук більше, ніж Нюша, а Бараш на 12 менше, ніж Крош. Скільки всього фантиків подарували друзі Їжачку?

1. 34 + 8 = 42;
2. 42-12 = 30;
3. 34 + 42 + 30 = 106.

 

Задача 3.

Кар Карич забув порядок дій. Допоможіть йому.

444: 4 + (45 • 51-232: 2) • 6

 

Гімнастика для очей.

 

Дістаємо свої мобільні телефони, заходимо в програму Kahoot та виконуємо завдання:

1. Виконайте дії:

Приклад	Відповіді
1	А) Б) 1 (вірна відповідь) В)
1	А) Б) 4 (вірна відповідь) В)
	А) (вірна відповідь) Б) В)
Сума двох дробів дорівнює , а один із дробів . Знійдіть інший дріб.	А) Б) В)
Розв’яжіть рівняння :	А) Б) 40(вірна відповідь) В)

 

3. Повідомлення теми і мети уроку.

На початку року ми з вами вивчили натуральні числа, а потім всі дії з ними. Тепер ми вивчаємо звичайні дроби, а значить вивчаємо дії з ними.

У багатьох народів в давнину дроби називали ламаними числами. Правил дій з дробами було так багато, що вміння оперувати ними сприймалося як диво! Тому завжди і всюди знання дробів користувалося особливою пошаною і повагою.

Сьогодні ми продовжуємо вивчати перші дії з ними - це додавання і віднімання.

Отже, тема нашого уроку "Віднімання дробу від натурального числа».

Ми повинні:

• сформулювати правила віднімання дробу від натурального числа і повторити правила додавання і віднімання дробів з однаковими знаменниками ;

• навчитися застосовувати їх при вирішенні завдань і при обчисленні значень виразів.

 

4. Вивчення нового матеріалу

Давайте з вами повторимо додавання і віднімання дробів з однаковими знаменниками.

Нюша і Бараш розмальовували квадрат. Нюша фарбовувала червоним кольором, а Бараш - зеленим.

Яку частину квадрата замалювала Нюша? (7/25)

Яку частину - Бараш? (10/25)

Яку частину вони всього зафарбували? (17/25)

Яку арифметичну дію використовують в задачах, якщо потрібно знайти скільки всього? (Додавання).

Отже отримуємо, що 7/25 +10/25 = 17/25.

Тепер спробуємо сформулювати правило складання звичайних дробів з однаковими знаменниками.

Щоб скласти два дроби з однаковими знаменниками треба:

• скласти чисельники,

• знаменник залишити колишнім.

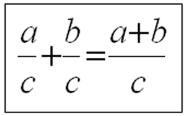
Наприклад: 3/14 +5/14 = 8/14

Учні вирішують приклади біля дошки і записують в зошити

19/24 + 3/24 = 22/24

17/29 + 9/29 = 26/29

21/45 + 17/45 = 38/45

А тепер повернемося до Нюші і Барашу.

На скільки частин Бараш зафарбував більше, ніж Нюша? (3/25)

Яку арифметичну дію використовують, якщо потрібно знайти на скільки одне число більше іншого? (Віднімання)

Отже отримуємо, що 10/25 -7/25 = 3/25.

Тепер спробуємо сформулювати правило віднімання звичайних дробів з однаковими знаменниками.

Щоб відняти два дроби з однаковими знаменниками треба:

• відняти чисельники цих дробів,

• знаменник залишити колишнім.

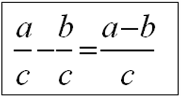
Наприклад: 7/15 - 4/15 = 3/15

Учні вирішують приклади біля дошки і записують в зошити.

Ті ж приклади, що були і на складання, тільки міняємо знак на мінус.

19/24 - 3/24 = 16/24

17/29 - 9/29 = 8/29

21/45 - 17/45 = 4/45

Чи можна відняти звичайний дріб від цілого числа?

Різниця числа 1 і правильного дробу – є дробом, що доповнює даний дріб до 1.

1. 3-
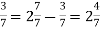
2. 5-

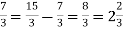
А зараз знайдемо це правило у підручнику. Читаємо на сторінці 238.

 

Тепер настав час для фізкультхвилинки.

 

5. Застосування отриманих знань при вирішенні задач.

1. Тренувальні вправи.

Давайте ще раз повторимо:

1. Як скласти два дроби з однаковими знаменниками?

2. Як відняти дроби з однаковими знаменниками?

3. Як відняти правильній дріб від одиниці?

4. Як відняти дріб від натурального числа?

Відкриємо підручники №1078, №1080, №1083

 

2. Самостійна робота.

Роздати картки учням.

Варіант 1

Обчисліть:

1.

2.

3. 

4. 

5. У книжці у Совуньї є кілька оповідань.

Перше оповідання займає 7/17 частин книги, а друге на 3/17 менше.

Яку частину займає друге оповідання?

(Відповіді: 1. 7/10; 2. 2/14; 3. 4/5; 4. 1/4; 5. 4/17)

 

Варіант 2

Обчисліть:

1.

2.

3. 

4. 

5. Дорога від будиночка Нюші до будиночка Бараша дорівнює км, а від будиночка Бараша до будиночка Кроша км.

 

Скільки кілометрів займає дорога від будиночка Нюші до будиночка Кроша?

 

Учням, які швидко впоралися із завданням, дати додаткове завдання.

 

1. На першій тарілці було 7/25 фунта вершкового масла, на другий тарілці на 3/25 фунта менше, а на третій - 4/25 фунта більше, ніж на першій. Скільки грамів масла було на трьох тарілках разом, якщо вважати фунт рівним 400 г? (22/25 фунта, 352 г)

2. Розв'яжіть рівняння (7/8)

 

6. Домашнє завдання.

П 27, №1079 1084, 1115.

 

7. Підсумок уроку.

Доповідь учнів з історії дробів.

 

З історії виникнення дробів:

З найдавніших часів у людей з'явилася потреба у вимірі довжин, площ, кутів і інших величин. Для отримання більш точних результатів міри стали ділити на частини, що призвело до появи дробів. Першими в практиці людей з'явилися найпростіші дроби (,). Лише значно пізніше греки, а потім індуси стали використовувати в обчисленнях і інші дроби.

 

Поняття "дріб" походить від дієслів "роздрібнювати", розбивати, ламати. А в перших підручниках математики дроби так і називалися - ламані числа.

Запис дробів за допомогою чисельника і знаменника з'явилася в Стародавній Греції, тільки греки знаменник записували зверху, а чисельник - знизу. У звичному для нас вигляді дріб вперше стали записуватися в Стародавній Індії близько 1500 років тому, але при цьому індуси обходилися без риси між чисельником і знаменником. А риса дробу стала вживатися тільки з 16 століття.

 

А тепер покажіть які споруди ви отримали з деталей конструктора.

 

За кількістю деталей у ваших спорудах ви отримуєте оцінки.

 

Урок закінчено!

 

Дякую за увагу!