Урок "Комбінаторні задачі"

                                              Урок у 5 класі

Тема.  Комбінаторні задачі

Мета. Формування вмінь розв’язувати найпростіші комбінаторні задачі методом перебору можливих варіантів; розвивати комбінаторне мислення; виховувати стохастичну культуру

Тип уроку. Урок засвоєння нових знань, умінь

Обладнання. Набір креслярського приладдя, таблиці, інструктивні картки

Метод. Пояснювально-ілюстративний з елементами гри, метод самоаналізу та колективної творчості

                                                         Хід уроку

І. Організаційний момент

  Діти, сьогодні у нас на уроці присутні гості – це мої консультанти, учні 11 класу

ІІ. Повідомлення теми уроку

ІІІ. Мотивація навчальної діяльності

    В житті дуже часто приходиться розв’язувати задачі, які мають декілька різних варіантів рішень і, щоб зробити правильний вибір, важливо жоден з них не пропустити. Для цього треба уміти перебрати всі можливі варіанти або комбінації і порахувати їх кількість.

     Задачі, які вимагають таких рішень називаються комбінаторними, а розділ математики, в якому розв’язуються такі задачі називається комбінаторикою.

  Комбінаторні задачі люди розв’язували ще в глибоку давнину. Вже декілька десятиліть назад в стародавньому Китаї захоплювались складанням магічних квадратів, в яких числа розташовували так, що їх сума по всім горизонталям і головним діагоналям була однаковою.

 

      

 

 

 

 

 

 

 

 

 

 

 

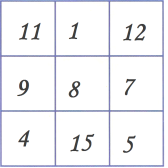
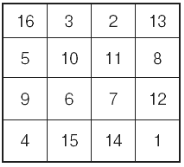
 Комбінаторні задачі виникли в зв’язку з такими іграми, як шашки, шахи, доміно, карти і т. д.

   Тепер комбінаторику використовують в усіх областях науки і техніки: в біології, хімії, механіці і т.д.

 

 ІV. Формування нових знань

 

    Давайте зараз розв’яжемо задачі за  допомогою складання  дерева  можливих варіантів, так званого  графа.

         Розпочнемо гру, де  розв’язувати задачі будуть « Конструктори» та «Наукові діячі».     Задача 1. Записати всі трицифрові числа цифрами 1,2,3 без повторень.

     Скільки таких чисел можна записати?

         Будуємо граф (рис.1)

 1)  На партах лежать картки, цифри на них відповідають номеру ряду, на якому вони сидять.

 2) З кожного ряду виходять по одному учню з цифрами номерів свого ряду : ( 1;2;3).

 3) Потім до кожного учня виходять два учня з цифрами відмінними від попередньої: (2,3;1,3;1,2).

 4) І знову до кожної пари виходять по одному учню з цифрами відмінними від попередньої, а саме:  (3;2;3;1;2;1)

 

 

 

 

 

                                                         

 

 

 

 

 

 

 

 

 

 

 

 

 

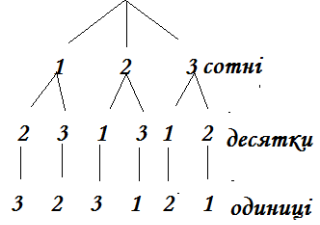
                                                        Рис.1

 

     Ми з вами зконструювали граф. Давайте тепер запишемо числа, які при цьому утворилися:

123; 132; 213; 231; 312; 321.

     Отже, можна скласти 6 чисел.

Відповідь: 6 чисел.

V.  Первинне застосування знань

     Зараз ви діти самостійно побудуєте граф.

Задача2.

Скільки двоцифрових чисел можна записати використовуючи цифри 1,2,3?

Цифри можуть повторюватись.

 

                                        

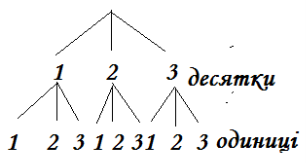
                                                           Рис.2  

Утворилися числа:

11; 12; 13; 21; 22; 23; 31; 32; 33

Відповідь: 9 двоцифрових чисел.

Молодці, ви гарно справилися з поставленим завданням, будуючи граф (рис.2).

   А зараз прошу розділитися на дві команди «Наукові діячі» та «Конструктори».

Розв’яжемо задачу. 

Восьмеро учнів повинні будуть взяти участь у турнірі з шашок так, щоб кожен зіграв з кожним одну партію.

   Скільки  всього партій буде зіграно?

Наукові діячі розв’яжуть  задачу за допомогою математичних суджень, а конструктори будуючи граф.

Наукові діячі   стверджують, що:

 перший учень може зіграти 7 партій;

другий може зіграти 6 партій (відкидаємо 1,2 гравця);

третій - 5 партій (без 1,2,3);

четвертий – 4 партії (без 1,2,3,4);

п'ятий – 3 партії ( без 1,2,3,4,5);

шостий- 2 партії (без 1,2,3,4,5,6);

сьомий – 1 партію (без 1,2,3,4,5,6,7).

Всього 7+6+5+4+3+2+1= 28 партій.

Конструктори представили  своє розв’язання у вигляді графа ( рис.3)

 

  

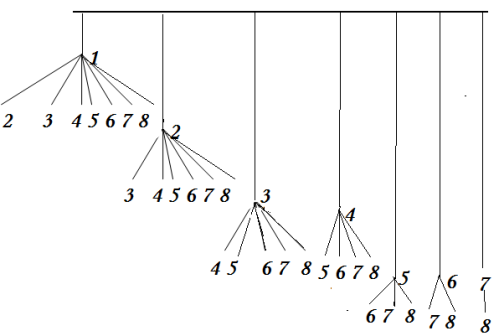
                                                                    Рис.3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Отже,  1+2+3+4+5+6+7= 28 партій.

Відповідь: 28 партій.

V. Підсумки уроку

Сьогодні на уроці ми познайомилися з комбінаторними задачами та деякими способами їх розв’язання.

Виставлення оцінок.

VІ. Домашнє завдання

 1) Вивчити §3 п.24.

 2) Розв’язати задачі №653, № 656, №659

 3) Для сильних учнів :

     а) №670

     б) заповнити магічний квадрат:

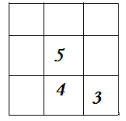
   в) Чотири подруги купили чотири білети в кінотеатр. Скількома різними способами вони можуть зайняти свої місця в глядацькому залі?