Урок математики у 5 класі: "Степінь з натуральним показником"

Відділ освіти, молоді та спорту

Великобагачанської районної державної адміністрації

Методичний кабінет

Радивонівської ЗОШ І – ІІІ ступенів

Урок з математики

5 клас

Підготувала і провела

учитель математики

Радивонівської ЗОШ І-ІІІ ступенів

Іванова Світлана Григорівна

с. Радивонівка

Математика 5 клас

Урок № 55                                                               Дата проведення  12.12.2013

Тема. Степінь натурального числа з натуральним показником.

Мета: ознайомити учнів з поняттям степеня числа з натуральним по­казником та термінологією (основа степеня, показник степеня, степінь); навчити записувати добуток рівних множників у вигляді степеня і навпа­ки, а також знаходити значення виразів, що містять степінь; розвивати в учнів логічне мислення, уміння користуватися індукцією, дедукцією, розвивати увагу, культуру мовлення та математичну культуру учнів, сприяти формуванню та розвитку інтелектуальних і творчих здібностей учнів, прищеплювати інтерес до математики; продовжити формувати в учнів науковий світогляд і раціональне математичне мислення, виховання працьовитості, позитивне ставлення до навчання і відповідальність за свої досягнення, наполегливості в подоланні труднощів.

Тип уроку: засвоєння нових знань.

Обладнання: таблиця «Степінь з натуральним показником», проектор, комп'ютер.

Методи і прийоми: мультимедійна демонстрація, відгадування загадки, усні та письмові вправи, робота з підручником, тестові завдання.

Хід уроку

І. Організаційний момент

    Привітання з класом. Перевірка присутності учнів.

ІI. Актуалізація опорних знань

ІV. Формування нових знань. Пояснюю матеріал, пояснення супроводжується показом презентації.

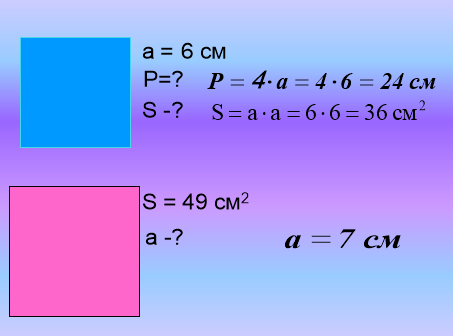
 Поставити перед учнями завдання, що приведе їх до «відкриття» поняття степеня і розуміння суті запису до­бутку однакових множників у вигляді степеня.

 Завдання 1

Учні самі можуть встановити, що вирази в лівому стовпчику будуть дорівнювати добутку одних з рівних доданків на їх кількість у сумі, і помітити схожу закономірність у короткому запису добутку однакових множ­ників у вигляді а^b, де а — один з однакових множників, a b— число таких множників у добутку.

Як ти знаєш, за допомогою добутку зручно записувати суму кількох рівних доданків. Наприклад: 7 + 7 + 7 + 7 =  7 * 4.

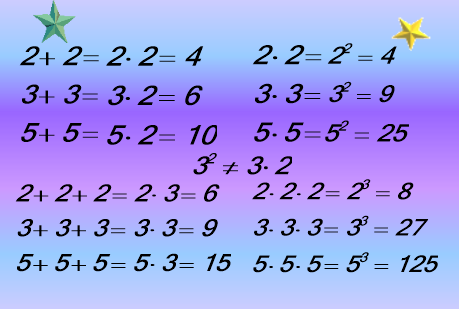
              У  математиці  придумали  спосіб   коротко  записувати добуток,  в якому всі множники рівні.

              Наприклад: 7 * 7 * 7 * 7 =  7⁴.

              Вираз 7⁴  називають  степенем  і  читають  так :  «сім  у четвертому степені»   або   «сім   у  степені  чотири».   При  цьому число 7 називають основою   степеня,  а  число  4 – показником   степеня.  Число  4  показує, скільки  разів число 7 бере участь у добутку.

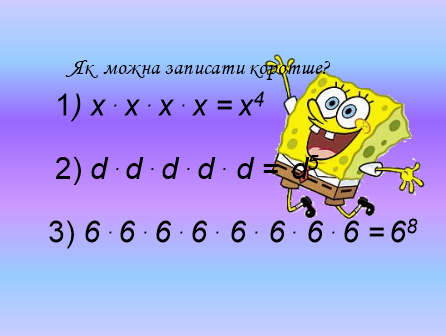
Після цього даю означення степеня деякого числа а з нату­ральним показником п, називаю основні терміни, пов'язані з поняттям степеня (основа, показник степеня, степінь, піднесення до степеня), ос­новними властивостями степеня (а¹ = а; 1^п = 1; 0^п = 0), даю назву другому і третьому степеню числа а   (а² — квадрат числа а, b³ — куб числа b) і фор­мулюю правило виконання дій у виразі, що містить степінь (учні роблять короткі записи в зошитах відповідно до схеми «Степінь з натуральним по­казником»).

Степінь з натуральним показником

   Приклади:

3⁵ = 3 · 3 · 3 · 3 · 3  = 243

5³ = 5 · 5 · 5 = 125,

10² = 10 · 10 = 100.

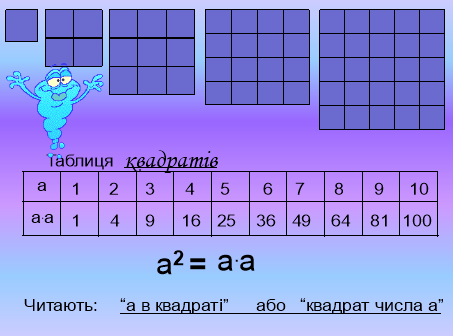
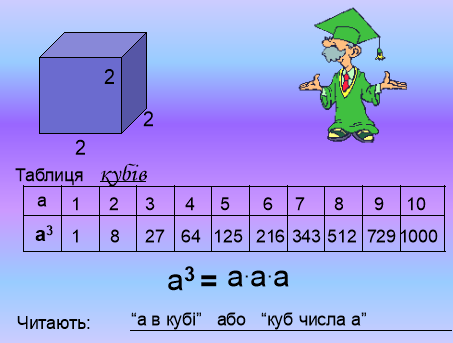
             Другий    степінь також  називають  квадратом  числа.  Наприклад,    запис  а²  читають  «а в квадраті».  Третій степінь  числа називають кубом числа, і запис а³  читають «а в кубі».

             Чи може показник степеня дорівнювати одиниці? Може! І оскільки не прийнято розглядати добуток, який складається з одного множника, то просто домовилися, що а¹  =а.

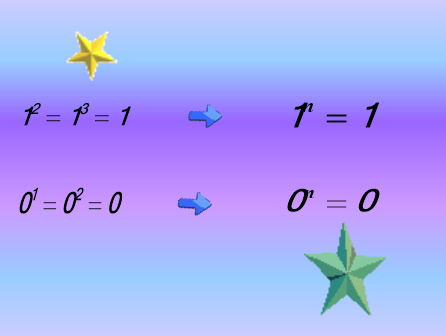
             Наприклад:  2¹  = 2,    17¹ = 17.

             Звернемо  увагу,  що піднесення  числа  до  степеня  –  це  нова, п`ята, арифметична дія. Визначимо черговість її виконання при знаходженні значення числового виразу.

            Якщо, в числовий вираз  входить степінь, то спочатку  виконують   піднесення   до   степеня,  а   потім   інші   дії.

  Наприклад: 5 · 2²   =  5 · 4 = 20,

                        5 + 2²   =  5 + 4 = 9.

V. Закріплення матеріалу

На закріплення термінології – усно:

1. Назвіть основу і показник степеня: 1) 4⁸;  2) 13¹⁰;  3) а⁹;  4) 2³⁹;  5) 93¹.
2. Який із записів неправильний? Чому?

1) 9 · 9 = 2⁹;  2) 10 · 10 · 10 = 10³;  3) b · b = b²;

4) ;  5) 5 · 6 · 6 · 6 = 6⁴.

3. Прочитайте вираз і знайдіть його значення:

1) 3¹;  2) 1¹⁰;  3) 0²⁵;  4) 5²;  5) 2³;  6) 3⁴.

 Після цього слід запропонувати учням письмово виконати вправи:

№ 674, 675 — на обчислення значень виразів, що містять степінь. Прочитати вирази за допомогою слів «сума», «різниця», «добуток», «частика», «квадрат», «куб» числа.

№ 680. Спрямований на попередження помилок у встановленні по­рядку виконання дій у виразах, що містять степінь.

VІ. Підсумок уроку

Тестові запитання класу

1. Як називається запис 5⁴?
2. Як називається число 5 в цьому запису? Що воно показує?
3. Як називається число 4 в цьому запису? Що воно показує?
4. Як піднести 5 до четвертого степеня?
5. Чи правильно виконані дії у прикладі 5 · 2² = 10² = 100? Чому? Яка відповідь правильна?

VІІ. Домашнє завдання