Урок "Побудова графік функції"

УРОК  № ______                                                                          (алгебра 7 клас)

Тема уроку: Побудова графік функції

Цілі уроку: розвивати в учнів розуміння поняття «графік функції», формувати вміння будувати й читати графіки функцій, досліджувати їх властивості; розвивати пізнавальну компетентність та компетентність продуктивної творчої діяльності, розвивати просторову уяву, творчі здібності, мислення, графічну культуру;  виховувати ініціативу, старанність, інтерес до математики, спостережливість, зацікавленість у пізнанні нового.

Очікувані результати: учні повинні знати означення графіка функції, вміти будувати і читати графіки функцій.

Тип уроку: комбінований.

Обладнання: підручник, конспект, дидактичний матеріал.

Хід уроку

І. Організаційний етап.

Перевірка готовність учнів до уроку. Повідомлення плану роботи.

ІІ. Перевірка домашнього завдання.

Взаємоперевірка за допомогою зразка.

ІІІ. Актуалізація опорних знань.

Інтерактивна вправа «Мозковий штурм»

1.     Вкажіть область визначення функції, заданої формулою у=х²+5.
2.     Чи існує таке значення аргументу, при якому функція 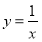дорівнює 0?
3.     Чи існує таке значення аргументу, при якому значення функції

  у=х²+(х-1)² дорівнює 0?

4.     Якого  значення набуває функція у=-х+1 при х=-1?
5.     Функція задана формулою у=12х
   1. Яка змінна є незалежною?
   2. Яка змінна є залежною?
   3. Яка змінна є функцією?
6. Що називають графіком функції?

Графіком функції називають геометричну фігуру, яка складається з усіх тих і тільки тих точок координатної площини, абсциси яких дорівнюють значенню аргументу, а ординати – відповідним значенням функції.

7. Як побудувати графік функції?

Щоб побудувати графік функції, потрібно надати аргументам функції довільні значення й обчислити відповідні значення функції.

Запитання для фронтальної бесіди:

– Що називається прямокутною системою координат? координат­ною площиною?

– Скільки точок із координатами (-2; 3) можна зобразити на коор­динатній площині?

– Де на координатній площині розташовані точки з координата­ми: (0;-4); (5;0); (3;3); (-2; 2)?

ІV. Мотивація навчальної діяльності.

Слово вчителя

На попередньому уроці ми встановили, що, якщо функція задана формулою, то можна скласти як завгодно багато пар значень (х; у), де х – незалежна зміна (значення аргументу); у – відповідне значення функції. Кожна пара (х; у) зображується точкою на координатній площині. Виникає запитання: скільки таких точок можна побудувати і як це пов’язано з функцією?

Опрацювавши домашнє завдання учні розглянули у підручнику приклад побудови графіка функції і прокоментувати його.

Чи будь-яка фігура, зображена на координатній площині, може бути графіком функції?

Щоб фігура, яку зображено на координатній площині, була графіком деякої функції необхідно, щоб кожна пряма, перпендикулярна до осі абсцис, перетинала цю фігуру не більше, ніж в одній точці.

4. Які умови виконуються, якщо фігура є графіком функції?

Якщо якась фігура є графіком функції, то виконуються дві умови:

1. якщо х₀ – деяке значення аргумента, а f(х₀) – відповідне значення функції, то точка з координатами (х₀; f(х₀)) обов’язково належить графіку;
2. якщо (х₀; y₀) – координати довільної точки графіка, то х₀ і y₀ – відповідні значення незалежної і залежної змінних функції f, тобто y₀ = f(х₀).

5. На які запитання можна знайти відповідь, вивчаючи графік функції?

За даним рисунком дати відповіді на запитання.

Вивчаючи графік функції, можна знайти:

1. область визначення функції;
2. область значень функції;
3. значення аргументу, при яких значення функції дорівнює нулю (нулі функції);
4. значення аргументу, при яких значення функції набуває додатних значень;
5. значення аргументу, при яких значення функції набуває від’ємних значень.

VІ. Закріплення нових знань і вмінь.
 

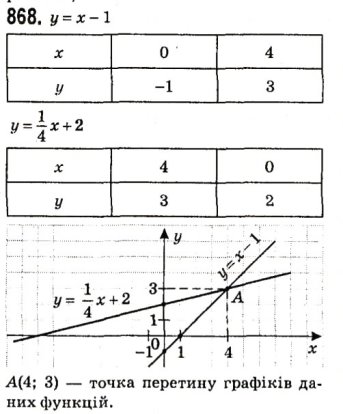
VIІ. Підсумки уроку. Рефлексія.

Бліц-опитування

1. Що називають графіком функції?
2. Як можна побудувати графік функції?
3. Яка фігура не може бути графіком функції?
4. Що можна з’ясувати, вивчаючи графік функції?

«Кольорова феєрія»

На столі в учнів лежать стіки трьох кольорів (зелений, жовтий, червоний), які відповідно означають «Мені все зрозуміло», «Мені дещо незрозуміло», «Мені складно зрозуміти». Вчитель називає основні питання теми і просить учнів показати стіки, визначає основні завдання на наступний урок.

Вчитель підводить підсумок уроку та оцінює учнів.

VIIІ. Домашнє завдання.

____________________________________________________________