Володимир-Волинський район Зимнівська ОТГ

Селецька загальноосвітня школа І-ІІ ступенів імені Олени Полонської – філія освітнього опорного закладу навчально-виховного комплексу "Загальноосвітня школа І-ІІІ ступенів-ліцей" с. Зимне

Методика вивчення теми «Цілі вирази» (методичні рекомендації)

             а                    b

а2	аb
аb	b2

аа

Мазур Віра Миколаївна,

_bb                                                                        учитель математики

                ^{а                    b}                                                                          2022

Мазур Віра Миколаївна, учитель математики Селецької загальноосвітньої школи І-ІІ ступенів імені Олени Полонської – філії освітнього опорного закладу навчально-виховного комплексу "Загальноосвітня школа І-ІІІ ступенів-ліцей" с. Зимне Володимир-Волинського району Волинської області, старший учитель

Методичні рекомендації укладено відповідно до чинної навчальної програми з алгебри для загальноосвітньої школи. Допоможуть вчителю математики у підготовці уроків алгебри у 7 класі по темі «Цілі вирази». Вони забезпечують зв’язок між різними галузями знань та допомагають формувати в здобувачів освіти уміння використовувати знання про властивості виразів у різних нестандартних ситуаціях. Рекомендовано для вчителів математики та здобувачів освіти.

Рецензенти: Матвіюк Ю.В., керівник спільноти вчителів математики;                              ТрачукТ.В.,  доцент кафедри теорії та методики викладання шкільних предметів ВІППО, кандидат педагогічних наук.

Обговорено та схвалено на засіданні науково-методичної ради ООЗ НВК «ЗОШ І-ІІІ ст. – ліцей» с. Зимне (протокол №4 від 21.01.2022 р.) для представлення на ХХVІІ обласну виставку дидактичних і методичних матеріалів «Творчі сходинки педагогів Волині».

ЗМІСТ

                          ВСТУП     

РОЗДІЛ 1. ПСИХОЛОГІЧНІ ОСОБЛИВОСТІ НАВЧАННЯ МАТЕМАТИКИ РОЗДІЛ 2. СКЛАДОВІ ТЕМИ «ЦІЛІ ВИРАЗИ» чинної програми та їх короткий аналіз 14

                          РОЗДІЛ 3.   МЕТОДИКА ВИВЧЕННЯ ТЕМИ «ЦІЛІ ВИРАЗИ» 43

3.1. Різні способи розкладання на

                       множники чотиричленів                      ⁶⁹ 3.2. Різні способи розкладання на 82

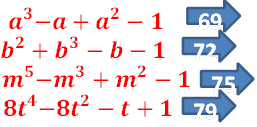                                                                     множники тричленів

                               ВИСНОВКИ      109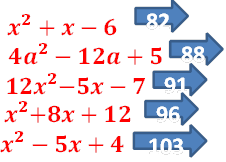                               

ЛІТЕРАТУРА 111

3

                                                                                                                                                 ВСТУП  

Вирази супроводжують шкільну математичну освіту від початкової ланки і до вищої. Недаремно значна частина шкільної математики присвячена перетворенням різних виразів, що обумовлено необхідністю їх детального вивчення. Саме тому, знайомлячись із новим предметом алгебра, семикласники півроку вивчають тему «Цілі вирази». Визначенню основних понять (тотожності) перетворень цілих алгебраїчних виразів, властивостей степеня з натуральним показником, формулам скороченого множення відводиться у курсі 7 класу 30 годин.

З найпростішими числовими виразами учні знайомляться ще в початковій школі, знаходять значення виразів, але про визначення понять „вираз”, „значення виразу” мова не йде. Також не дається визначення виразу зі змінною, хоча вони є. (Поняттю „вираз” взагалі в школі не дається строгого означення). У 5 класі говорять про спрощення виразів, яке виконується на основі властивостей арифметичних операцій. Ні про яке додавання подібних доданків, винесення коефіцієнта, спільного множника в 5 класі не йдеться.

У 6 класі апарат тотожних перетворень розширюється у зв’язку з розвитком поняття числа. Тут учні вже фактично виконують зведення многочлена до стандартного виду (зведення подібних членів), але називають це поки що зведенням подібних доданків. В цьому ж класі учні вивчають правила розкриття дужок (перед якими стоїть знак „+” або „-”), вивчається поняття „коефіцієнт”. Тобто, у 5-6 класах виконується спрощення цілих алгебраїчних виразів 1-го степеня на основі властивостей арифметичних дій.

Системне вивчення тотожних перетворень починається в 7 класі, коли вводяться строгі математичні означення таких понять, як „тотожність”, „тотожно рівні вирази”, „тотожне перетворення виразів”. Учитель повинен донести семикласнику, що сутність тотожних перетворень складається в:

•         застосуванні до виразу відомих означень і властивостей тих операцій, які вказані в даному виразі;

•         додаванні до виразу іншого, тотожно рівного нулю;  множенні його на вираз, тотожно рівний 1.

Тут виконується зведення одночлена і многочлена до стандартного виду, множення одночлена на многочлен і многочлена на многочлен, розкладання многочлена на множники, вивчаються формули скороченого множення. Отже, в 7 класі розглядаються цілі раціональні вирази.

                                           Розділ 1. Психологічні особливості навчання математики                    

Зміст навчального матеріалу

Навчити дітей математики – це означає сформувати математичні компетентності. Математична компетентність – це уміння бачити та застосовувати математику в реальному житті, вміння досліджувати математичні моделі математичними методами.

Вивчення математики у 5-6 класах здійснюється з переважанням індуктивних міркувань в основному на наочно-інтуїтивному рівні із залученням практичного досвіду учнів і прикладів із довкілля. Відбувається поступове збільшення теоретичного матеріалу, який вимагає обґрунтування тверджень, що вивчаються. Це готує учнів до ширшого використання дедуктивних методів на наступному етапі вивчення математики.

Психологічні особливості навчання математики

Зміст навчального матеріалу

Загальноосвітня мета викладання математики вимагає від учителя наступне, а саме: передати учням певну сукупність математичних знань, умінь та навичок; навчити письмовій та усній математичним мовам; навчити застосовувати набуті знання при розв'язанні найпростіших завдань; ознайомити з методами пізнання реального світу, математичними елементами.

Психологічні особливості навчання математики

Зміст навчального матеріалу

Методика навчання математики дуже тісно пов’язана із психологією. Психологія – це основа методики, без неї методика стає безпредметною. Оскільки не можна говорити про раціональні методи навчання школярів, не знаючи їх психологічних властивостей: як вони сприймають, думають, пригадують, запам’ятовують. Будь-яка спроба розв’язати те чи інше конкретне питання методики математики без урахування відомостей психології не увінчається успіхом [5].

Психологічні особливості навчання математики

Зміст навчального матеріалу

Урок математики – це пізнавальний діалог між учителем і учнем, при якому колективна робота всього класу вдало поєднується з активною самостійною діяльністю кожного учня. На уроках вчитель намагається розвивати мислення і творчі здібності учнів, виховувати особистість, постійно залучає учнів до обміну думками, аналізу помилкових тверджень, аргументованого захисту одержаних висновків. Реалізація індивідуального підходу починається з вивчення готовності дитини до навчання. Не менш важливо є звернути увагу на фізичний стан і здоров’я дитини, від яких залежить увага на уроці. Впровадження цього підходу спрямоване на створення у кожного учня ділового настрою, пробудження інтересу до вивчення тієї чи іншої теми.

Психологічні особливості навчання математики

Зміст навчального матеріалу

Психологічний аспект полягає у встановленні неповторності учня, у визначенні його ставлення до оточуючих і до себе і специфіки реагування на зовнішні впливи. Учитель може захопити учнів своїми розповідями про математику та її значення в житті людини. Навчальний процес повинен бути зорієнтованим на досягнення максимально значущих результатів кожним учнем і, що не менш важливе, на розвиток логічного мислення, пізнавальних можливостей та інтересів.

                                              Психологічні особливості навчання математики                                           

Доцільно учнів навчати на основі різних історичних відомостей і математичних фактів. Так, вивчаючи квадрат двочлена доцільно розповісти, що формули скороченого множення стародавнім китайським і грецьким математикам були відомі за багато віків до початку нашої ери. Записували їх тоді не за допомогою букв, а словами і доводили геометрично (тільки для додатних чисел).

                                                                                                                             Користуючись                                                        малюнком,                                                       пояснювали,             що

                а                      b

а2	аb
аb	b2

                                                                                                              для   будь-яких   додатних                                  чисел а і b площа

а

аквадрата зі стороною а+b дорівнює сумі площ двох квадратів зі сторонами а і b та двох

_bb                                          прямокутників зі сторонами а та b.

                   а                      b

РОЗДІЛ 2. СКЛАДОВІ ТЕМИ «ЦІЛІ ВИРАЗИ» чинної програми та їх короткий аналіз

Навчальна програма з математики

(Навчальна програма для учнів 5-9 класів загальноосвітніх навчальних закладів, затверджена Наказом Міністерства освіти і науки України від 07.06.2017 № 804)

(7 клас, алгебра, 70 год, 2 год на тиждень)

№ з/п	Зміст навчального матеріалу	Кількість годин
1	ЦІЛІ ВИРАЗИ	30
2	ФУНКЦІЇ	10
3	ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ	18
4	ПОВТОРЕННЯ І СИСТЕМАТИЗАЦІЯ НАВЧАЛЬНОГО МАТЕРІАЛУ	12

Мета базової загальної середньої освіти:

Зміст навчального матеріалу

розвиток та соціалізація особистості учнів, формування їхньої національної самосвідомості, загальної культури, світоглядних орієнтирів, екологічного стилю мислення і поведінки, творчих здібностей, дослідницьких навичок і навичок життєзабезпечення, здатності до саморозвитку та самонавчання в умовах глобальних змін і викликів.

Навчальна програма з математики

Випускник основної школи — це патріот України, який знає її історію; носій української культури, який поважає культуру інших народів; компетентний мовець, що вільно спілкується державною мовою, володіє також рідною (у разі відмінності) й однією чи кількома іноземними мовами, має бажання і здатність до самоосвіти, виявляє активність і відповідальність у громадському й особистому житті, здатний до підприємливості та ініціативності, має уявлення про світобудову, бережно ставиться до природи, безпечно й доцільно використовує досягнення науки і техніки, дотримується здорового способу життя.

Навчальна програма з математики

Провідним засобом реалізації вказаної мети є запровадження компетентнісного    підходу     у     навчально-виховнийий   процес загальноосвітньої школи шляхом формування предметних і ключових компетентностей. Курс математики основної школи логічно продовжує реалізацію завдань математичної освіти учнів, розпочату в початкових класах, розширюючи і доповнюючи ці завдання відповідно до вікових і пізнавальних можливостей школярів.

Навчальна програма з математики

В основу побудови змісту та організації процесу навчання математики покладено компетентнісний підхід, відповідно до якого кінцевим результатом навчання предмета є сформовані певні компетентності, як здатності учня застосовувати свої знання в навчальних і реальних життєвих ситуаціях, повноцінно брати участь в житті суспільства, нести відповідальність за свої дії. Навчання математики в основній школі передбачає формування предметної математичної компетентності. Формування зазначеної компетентності підпорядковується реалізації загальних завдань шкільної математичної освіти.

Навчальна програма з математики загальні завдання шкільної математичної освіти

•         формування ставлення до математики як невід’ємної складової загальної культури людини, необхідної умови її повноцінного життя в сучасному суспільстві на основі ознайомлення з ідеями і методами математики як універсальної мови науки і техніки, ефективного засобу моделювання і дослідження процесів і явищ навколишнього світу;

•         забезпечення оволодіння математичною мовою, розуміння ними математичної символіки, математичних формул і моделей як таких, що дають змогу описувати загальні властивості об’єктів, процесів та явищ;

Навчальна програма з математики загальні завдання шкільної математичної освіти

•         формування здатності логічно обґрунтовувати та доводити математичні твердження, застосовувати математичні методи у процесі розв’язування навчальних і практичних задач, використовувати математичні знання і вміння під час вивчення інших навчальних предметів;

•         розвиток умінь працювати з підручником, опрацьовувати математичні тексти, шукати і використовувати додаткову навчальну інформацію, критично оцінювати здобуту інформацію та її джерела, виокремлювати головне, аналізувати, робити висновки, використовувати отриману інформацію в особистому житті;

Навчальна програма з математики загальні завдання шкільної математичної освіти

•         формування здатності оцінювати правильність і раціональність розв’язування математичних задач, обґрунтовувати твердження, приймати рішення в умовах неповної, надлишкової, точної та ймовірнісної інформації.

Крім цих загальних освітніх завдань в основній школі реалізуються такі специфічні для даного етапу навчання математики освітні завдання:

•         розширення знань про число (від натуральних чисел до дійсних), формування культури усних, письмових, інструментальних обчислень;

•         формування системи функціональних понять, умінь використовувати функції та їх графіки для характеристики залежностей між

величинами, опису явищ і процесів;

Навчальна програма з математики загальні завдання шкільної математичної освіти

•         забезпечення оволодіння учнями мовою алгебри, уміннями здійснювати перетворення алгебраїчних виразів, розв’язувати рівняння, нерівності та їх системи, моделювати за допомогою рівнянь реальні ситуації, пояснювати здобуті результати;

•         формування знань про геометричні фігури на площині, їх властивості, а також умінь застосовувати здобуті знання у навчальних і життєвих ситуаціях;

•         ознайомлення зі способами і методами математичних доведень, формування умінь їх практичного використання.

Навчання математики має зробити певний внесок у формування ключових компетентностей Навчальна програма з математики

Компетентність

Компоненти

1.Спілкування державною (і рідною, у разі відмінності) мовами

Уміння: ставити запитання і розпізнавати проблему; міркувати, робити висновки на основі інформації, поданої в різних формах (у таблицях, діаграмах, на графіках); розуміти, пояснювати і перетворювати тексти математичних задач (усно і письмово), грамотно висловлюватися рідною мовою; доречно та коректно вживати в мовленні математичну термінологію, чітко, лаконічно та зрозуміло формулювати думку, аргументувати, доводити правильність тверджень; поповнювати свій словниковий запас. Ставлення: розуміння важливості чітких та лаконічних формулювань. Навчальні ресурси: означення понять, формулювання властивостей, доведення теорем.

 

Компетентність	Компоненти
2. Спілкування іноземними мовами	Уміння: спілкуватися іноземною мовою з використанням числівників, математичних понять і найуживаніших термінів; ставити запитання, формулювати проблему; зіставляти математичний термін чи буквене позначення з його походженням з іноземної мови, правильно використовувати математичні терміни в повсякденному житті. Ставлення: усвідомлення важливості вивчення іноземних мов для розуміння математичних термінів та позначень, пошуку інформації в іншомовних джерелах. Навчальні ресурси: тексти іноземною мовою з використанням статистичних даних, математичних термінів.

 

Компетентність		Компоненти
3. Мате матична	Уміння: оперувати числовою інформацією, геометричними об’єктами на площині та в просторі; встановлювати відношення між реальними об’єктами навколишньої дійсності (природними, культурними, технічними тощо); розв’язувати задачі, зокрема практичного змісту; будувати і досліджувати найпростіші математичні моделі реальних об'єктів, процесів і явищ, інтерпретувати та оцінювати результати; прогнозувати в контексті навчальних та практичних задач; використовувати математичні методи у життєвих ситуаціях. Ставлення: усвідомлення значення математики для повноцінного життя в сучасному суспільстві, розвитку технологічного, економічного й оборонного потенціалу держави, успішного вивчення інших дисциплін. Навчальні ресурси: розв'язування математичних задач, зокрема таких, що моделюють реальні життєві ситуації.

 

Компетентність

Компоненти

4.Основні компетентності у природничих науках і технологіях

Уміння: розпізнавати проблеми, що виникають у довкіллі і які можна розв’язати засобами математики; будувати та досліджувати математичні моделі природних явищ і процесів. Ставлення: усвідомлення важливості математики як універсальної мови науки, техніки та технологій. Навчальні ресурси: складання графіків та діаграм, які ілюструють функціональні залежності результатів впливу людської діяльності на природу.

 

Компетентність

Компоненти

5. Інформаційноцифрова

Уміння: структурувати дані; діяти за алгоритмом та складати алгоритми; визначати достатність даних для розв’язання задачі; використовувати різні знакові системи; знаходити інформацію та оцінювати її достовірність; доводити істинність тверджень. Ставлення: критичне осмислення інформації та джерел її отримання; усвідомлення важливості ІКТ для ефективного розв’язування математичних задач. Навчальні ресурси: візуалізація даних, побудова графіків та діаграм за допомогою програмних засобів.

 

Компетентність

Компоненти

6. Уміння вчитися впродовж життя

Уміння: визначати мету навчальної діяльності, відбирати й застосовувати потрібні знання та способи діяльності для досягнення цієї мети; організовувати та планувати свою навчальну діяльність; моделювати власну освітню траєкторію, аналізувати, контролювати, коригувати та оцінювати результати своєї навчальної діяльності; доводити правильність власного судження або визнавати помилковість. Ставлення: усвідомлення власних освітніх потреб та цінності нових знань і вмінь; зацікавленість у пізнанні світу; розуміння важливості вчитися впродовж життя; прагнення до вдосконалення результатів своєї діяльності. Навчальні ресурси: моделювання власної освітньої траєкторії.

 

Компетентність	Компоненти
7. Ініціативність і підприємливість	Уміння: генерувати нові ідеї, вирішувати життєві проблеми, аналізувати, прогрозувати, ухвалювати оптимальні рішення; використовувати критерії раціональності, практичності, ефективності та точності, з метою вибору найкращого рішення; аргументувати та захищати свою позицію, дискутувати; використовувати різні стратегії, шукаючи оптимальних способів розв’язання життєвого завдання. Ставлення: ініціативність, відповідальність, упевненість у собі; переконаність, що успіх команди – це й особистий успіх; позитивне оцінювання та підтримка конструктивних ідей інших. Навчальні     ресурси: задачі   підприємницького    змісту     (оптимізаційні задачі).

 

Ключові компетентності		Компоненти
8. Соціальна і громадянська компетентності	Уміння: висловлювати власну думку, слухати і чути інших, оцінювати аргументи та змінювати думку на основі доказів; аргументувати та відстоювати свою позицію; ухвалювати аргументовані рішення в життєвих ситуаціях; аналізувати власну економічну ситуацію, родинний бюджет, користуючись математичними методами; орієнтуватися в широкому колі послуг і товарів на основі чітких критеріїв, робити споживчий вибір, спираючись, зокрема, і на математичні дані. Ставлення: ощадливість і поміркованість; рівне ставлення до інших незалежно від статків, соціального походження; відповідальність за спільну справу; налаштованість на логічне обґрунтування позиції без передчасного переходу до висновків; повага до прав людини.

 

Компетентність

Компоненти

9. Обізнаність і самовираження у сфері культури

Уміння: здійснювати необхідні розрахунки для встановлення пропорцій, відтворення перспективи, створення об’ємнопросторових композицій; унаочнювати математичні моделі, зображати фігури, графіки, рисунки, схеми, діаграми. Ставлення: усвідомлення взаємозв’язку математики та культури на прикладах з архітектури, живопису, музики та ін.; розуміння важливості внеску математиків у загальносвітову культуру. Навчальні     ресурси:         математичні         моделі   в       різних         видах мистецтва.

 

Компетентність		Компоненти
10. Екологічна грамотність і здорове життя	Уміння: аналізувати і критично оцінювати соціально-економічні події в державі на основі статистичних даних; враховувати правові, етичні, екологічні і соціальні наслідки рішень; розпізнавати, як інтерпретації результатів вирішення проблем можуть бути використані для маніпулювання. Ставлення: ощадне та бережливе відношення до природніх ресурсів, чистоти довкілля та дотримання санітарних норм побуту; розгляд порівняльної характеристики щодо вибору здорового способу життя; власна думка та позиція до зловживань алкоголю, нікотину тощо. Навчальні ресурси: навчальні проекти, задачі соціально-економічного, екологічного змісту; задачі, які сприяють усвідомленню цінності здорового способу життя.

Навчальна програма з математики Наскрізні лінії та їх реалізація

Наскрізні лінії є засобом інтеграції ключових і загальнопредметних компетентностей, навчальних предметів та предметних циклів; їх необхідно враховувати при формуванні шкільного середовища.

Наскрізні лінії є соціально значимими надпредметними темами, які допомагають формуванню в учнів уявлень про суспільство в цілому, розвивають здатність застосовувати отримані знання у різних ситуаціях. Навчання за наскрізними лініями реалізується насамперед через:

організацію навчального середовища — зміст та цілі наскрізних тем враховуються при формуванні духовного, соціального і фізичного середовища навчання.

Коротка характеристика наскрізних ліній

1. Наскрізна лінія «Екологічна безпека й сталий розвиток» спрямована на формування в учнів соціальної активності, відповідальності та екологічної свідомості, готовності брати участь у вирішенні питань збереження довкілля і розвитку суспільства, усвідомлення важливості сталого розвитку для майбутніх поколінь.

Проблематика наскрізної лінії «Екологічна безпека та сталий розвиток» реалізується в курсі математики, насамперед, через завдання з реальними даними про використання природних ресурсів, їх збереження та примноження. Аналіз цих даних сприяє розвитку бережливого ставлення до навколишнього середовища, екології, формуванню критичного мислення, вміння вирішувати проблеми, критично оцінювати перспективи розвитку навколишнього середовища і людини. Можливі уроки на відкритому повітрі.

Коротка характеристика наскрізних ліній

2. Реалізація наскрізної лінії «Громадянська відповідальність» сприятиме формуванню відповідального члена громади і суспільства, що розуміє принципи і механізми функціонування суспільства. Ця наскрізна лінія освоюється в основному через колективну діяльність (дослідницькі роботи, роботи в групі, проекти тощо), яка поєднує математику з іншими навчальними предметами і розвиває в учнів готовність до співпраці, толерантність щодо різноманітних способів діяльності і думок.

Навчання математики має викликати в учнів якомога більше позитивних емоцій, а її зміст — бути націленим на виховання порядності, старанності, систематичності, послідовності, посидючості і чесності. Приклад вчителя покликаний зіграти важливу роль у формуванні толерантного ставлення до товаришів, незалежно від рівня навчальних досягнень.

Коротка характеристика наскрізних ліній

3. Завданням наскрізної лінії «Здоров'я і безпека» є становлення учня як емоційно стійкого члена суспільства, здатного вести здоровий спосіб життя. Наскрізна лінія «Здоров'я і безпека» в курсі математики реалізується через завдання з реальними даними про безпеку і охорону здоров’я (текстові завдання, пов’язані з середовищем дорожнього руху, рухом пішоходів і транспортних засобів, що стосуються чинників ризику). Особливо важливий аналіз причин ДТП, пов’язаних із перевищенням швидкості. Вирішення проблем, знайдених з «ага-ефектом» , пошук оптимальних методів розв’язування задач тощо, здатні викликати в учнів чимало радісних емоцій. Під «ага-ефектом» мається на увазі спільне вирішення задачі з ефектом раптового здогаду, «еврики».

Коротка характеристика наскрізних ліній

4. Наскрізна лінія «Підприємливість і фінансова грамотність» націлена на розвиток лідерських ініціатив, здатність успішно діяти в технологічному швидкозмінному середовищі, забезпечення кращого розуміння учнями практичних аспектів фінансових питань (здійснення заощаджень, інвестування, запозичення, страхування, кредитування тощо).

Ця наскрізна лінія пов'язана з розв'язуванням практичних задач щодо планування господарської діяльності та реальної оцінки власних можливостей, складання сімейного бюджету, формування економного ставлення до природних ресурсів. Вона реалізується під час вивчення відсоткових обчислень, рівнянь та функцій.

Навчальна програма з математики Умова формування компетентностей

Необхідною умовою формування компетентностей є діяльнісна спрямованість навчання, яка передбачає постійне включення учнів до різних видів педагогічно доцільної активної навчально-пізнавальної діяльності, а також практична його спрямованість. Доцільно, де це можливо, не лише показувати виникнення математичного факту із практичної ситуації, а й ілюструвати його застосування на практиці.

Навчальна програма з математики

Міжпредметні та внутрішньопредметні зв’язки

Формуванню математичної та ключових компетентностей сприяє встановлення та реалізація у навчанні математики міжпредметних і внутрішньопредметних зв’язків, а саме: змістово-інформаційних, операційно-діяльнісних і організаційно-методичних. Їх використання посилює пізнавальний інтерес учнів до навчання і підвищує рівень їхньої загальної культури, створює умови для систематизації навчального матеріалу і формування наукового світогляду. Учні набувають досвіду застосування знань на практиці та перенесення їх в нові ситуації.

Навчальна програма з математики Роль історичного матеріалу

Важливу роль у навчанні математики відіграє систематичне використання історичного матеріалу, який підвищує інтерес до вивчення математики, стимулює потяг до наукової творчості, пробуджує критичне ставлення до фактів, дає учням уявлення про математику як невід’ємну складову загальнолюдської культури. На дохідливих прикладах слід показувати учням, як розвивалися математичні поняття і відношення, теорії й методи. Ознайомлення учнів з іменами та біографіями видатних учених, які створювали математику, зокрема видатних українських математиків, сприятиме національному і патріотичному вихованню школярів.

Навчальна програма з математики

Характеристика навчального змісту і особливостей його реалізації

Зміст математичної освіти в основній школі структурується за такими змістовими лініями: числа; вирази; рівняння і нерівності; функції; геометричні фігури; геометричні величини. Кожна з них розвивається з урахуванням завдань вивчення математики на цьому ступені шкільної освіти, в якому виокремлюються два основні етапи: 5–6 класи і 7–9 класи. Освітні завдання на першому етапі реалізуються у процесі вивчення єдиного курсу математики, на другому — двох курсів: алгебри і геометрії.

                                               Навчальна програма з математики                                                             

Основні завдання курсу алгебри

•         формування умінь виконання тотожних перетворень цілих і дробових виразів,

•         посилення ролі обґрунтувань математичних тверджень, індуктивних і дедуктивних міркувань, формування різноманітних алгоритмів, що має сприяти розвитку логічного мислення і алгоритмічної культури школярів.

Основу  курсу   становлять  перетворення       раціональних та ірраціональних виразів. Важливо забезпечити формування умінь школярів виконувати основні види перетворень таких виразів, що є передумовою подальшого успішного засвоєння курсу.

А загалом на тему «Цілі вирази» відводиться половина навчальних годин, що заплановані програмою для 7 класу, де розглядається поняття степеня з цілим показником та його властивості.

РОЗДІЛ 3.    МЕТОДИКА ВИВЧЕННЯ ТЕМИ «ЦІЛІ ВИРАЗИ»

Перетворення цілих виразів являють собою одну із головних ліній шкільного курсу математики. Перетворення виразів є основою для розв’язування рівняннь і нерівностей, доведення тотожностей, обчислення значень буквених виразів.

Методика вивчення цілих виразів та їх перетвореннь

З найпростішими числовими виразами і буквеними учні ознайомились у 1 – 6 класах, вивчали найпростіші перетворення виразів за законами арифметичних дій. У курсі алгебри постає завдання – на основі вже здобутих знань і умінь систематизувати, поглибити і розширити знання, навички й уміння учнів про вирази та їх перетворення, навчити цілеспрямовано використовувати їх під час виконання різних навчальних задач.

Методика вивчення цілих виразів та їх перетвореннь

Програма з математики 5-9 класів, затверджена Наказом Міністерства освіти і науки України від 07.06.2017 № 804 передбачає в 7 класі повторити й уточнити відомості про числові та буквені вирази, формули, ввести поняття про тотожно рівні вирази, тотожність, тотожні перетворення виразів. У цьому класі вивчають тотожні перетворення цілих виразів (одночленів і многочленів), формули скороченого множення та застосування їх до перетворення многочленів.

Державні вимоги до знань і вмінь , набутих в результаті вивчення цілих виразів та їх перетворень

•           розрізняти числові вирази і вирази зі змінними, цілі вирази, тотожні вирази, одночлени, многочлени;

•           наводити приклади зазначених виразів

•           формулювати    означення   одночлена,     степеня з натуральним     показником,   многочлена,   подібних членів многочлена;

•           властивості степеня з натуральним показником;

•           правила множення одночлена і многочлена, множення двох многочленів.

Державні вимоги до знань і вмінь , набутих в результаті вивчення цілих виразів та їх перетворень

•           записувати і обґрунтовувати властивості степеня з натуральним показником та формули скороченого множення;

•           розв’язувати вправи, що передбачають: обчислення значень виразів зі змінними, зведення одночлена до стандартного вигляду, перетворення добутку одночлена і многочлена, суми, різниці, добутку двох многочленів у многочлен;

•           розкладання многочлена на множники способом винесення спільного множника за дужки, способом групування, за формулами скороченого множення та із застосуванням декількох способів, використання зазначених перетворень у процесі розв’язування рівнянь, доведення тверджень.

вивчення цілих виразів та їх

Основні поняттями теми «Цілі вирази»

•           «числовий вираз»,

•           «вираз зі змінними»,

•           «тотожно рівні вирази»,

•           «тотожність»,

•           «тотожне перетворення виразу»,

•           «одночлен»,

•           «многочлен».

вивчення цілих виразів та їх

У шкільному курсі математики означення поняття «вираз» давати недоцільно, адже сформулювати таке означення складно. Поняття про вирази (числові й буквені), тобто вирази зі змінною формулюють описово на конкретних прикладах. Учні мають навчитися розрізняти числові й буквені вирази. Учні мають свідомо усвідомити, що назва виразу визначається не тим виглядом, до якого його можна звести, а тим, який він має при заданні.

вивчення цілих виразів та їх

Поняття тотожно рівних виразів, тотожності вперше вводять до курсу алгебри 7 класу на рівні означень. Поняття тотожних перетворень виразів пояснюють описово на прикладах.

Поняття одночлена формують конкретно – індуктивним методом, розглядаючи приклади і вводять термін «одночлен». Важливо, щоб учні усвідомили істотну властивість одночленів, за якою вони відрізняються від інших виразів: одночлени є добутком чисел, змінних і степенів змінних.

вивчення цілих виразів та їх перетворень

Числовий множник одночлена, записаного у стандартному вигляді, називається коефіцієнтом одночлена. Він може бути будь-яким числом: цілим, дробовим, додатним, від’ємним, може дорівнювати одиниці. У такому разі одиницю перед буквеними множниками не записують.

Поняття стандартного вигляду одночлена, степеня одночлена також вводять описово на конкретних прикладах.

Поняття многочлена не спричиняє труднощів і означається, як сума одночленів. Складнішим для сприймання є поняття «цілого виразу», це пов’язано з тим, що термін «цілий вираз» в учнів асоціюється з поняттям цілого числа.

Методика вивчення цілих виразів та їх перетворень Раціональні вирази

3^х

                                                         6 · 2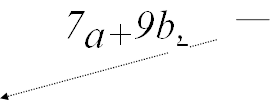,    _7с , (а + b)(а - b)

                                                              цілі вирази  дробові вирази

                                                                      2а,      5(2+1)                     7            ^а1

у а 2 числовізі змінними

                                                    6, 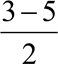, 42        7а, 4а+ b, 12а , 5х21

Методика вивчення цілих виразів та їх перетворень

Якщо вираз не містить інших дій, крім додавання, віднімання, множення, піднесення до степеня і ділення, його називають раціональним виразом

Вирази a+b, 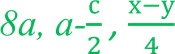 не містять  Вирази a :  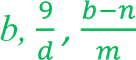містять

дії ділення на вираз зі змінними.     дію ділення на вираз зі змінними. Такі вирази називають цілими    Такі вирази називають дробовими

Методика вивчення цілих виразів та їх перетворень

Числовой вираз – це запис, що складається з чисел, сполучених знаками дій, і дужок, які вказують на порядок дій

49:7; 1,5 – 1,3; 3(7 – 12) .

Одне число також вважається числовим виразом

Вираз із змінною (алгебраїчний вираз) – це вираз, що складається з чисел і букв, які сполучені знаками дій і дужок, що вказують порядок дій

2 (а + b);     3 · а +2 · b;    9аb

Для скороченого запису знак множення “·” часто опускають Замість 3 · а +2 · b пишуть 3а+2b

Методика вивчення цілих виразів та їх перетворень

Серед записів один зайвий. Знайдіть його й поясніть, чому ви вважаєте його зайвим?

17 · 2 + 8

                                                                                           (14,2 - 11,4) : 4        (42 – b) · 0,4                               

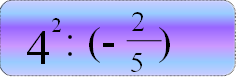
Якщо в числовому виразі виконати вказані дії, зберігаючи прийнятий порядок дій, то дістанемо число, яке називають значенням виразу

9 (6 – 10)

числовий вираз

 значення виразу

Методика вивчення цілих виразів та їх перетворень

Ділити можна тільки на число, яке не дорівнює нулю.

Якщо у виразі трапляється ділення на нуль, то говорять, що вираз не має змісту (на нуль ділити не можна).

                                                                              5:0   На 0 ділити не можна!!!

Методика вивчення цілих виразів та їх перетворень

В курсі алгебри перетворення розподіляються на 2 етапи:

1)     тотожні перетворення – перетворення виразів.

2)     рівносильні перетворення – перетворення формул.

У випадку, коли виникає потреба у спрощенні однієї частини формули, в ній виділяється вираз, який перетворюється (використовується певне тотожне перетворення). Відповідний предикат в цьому разі не змінюється.

Методика вивчення цілих виразів та їх перетворень

Наприклад: 15х – 6х = 36; 9х = 36.

Шкільна практика свідчить, що при вивченні різних видів тотожних перетворень доцільним є алгоритмічний підхід. Це означає, що вивчення кожного з видів перетворень має завершуватись (або починатись) формулюванням правила

(алгоритму) перетворення.

Методика вивчення цілих виразів та їх перетворень

Першим, новим для учнів перетворенням, з яким вони стикаються в курсі алгебри 7 класу, є зведення одночленів до стандартного вигляду. Мотивується це перетворення необхідністю спрощення одночлена, одержаного при множенні, утворенні добутку двох одночленів. Важливо при цьому підкреслити теоретичну основу виконання перетворення: у разі зведення одночлена до стандартного вигляду використовуються переставний a+b=b+a, сполучний закони множення (ab)c=a(bc) і правило множення степенів з однаковою основою а^m · аⁿ=а^m+n.

Після розгляду кількох прикладів варто сформулювати правило: щоб звести одночлен до стандартного вигляду, треба перемножити числові множники і степені змінних з однією основою; одержане число поставити в добутку на першому місці.

Вивчення множення одночленів завершується розв'язуванням кількох вправ на виконання оберненого перетворення – подання даного одночлена у вигляді добутку двох одночленів, з яких один заданого виду. Наприклад, представити одночлен – 48 а²b³c у вигляді добутку двох одночленів, з яких один є – 6 аb². Такі уміння потрібні будуть надалі під час розкладання многочленів на множники.

Піднесення одночленів до степеня не викликає труднощів в учнів. Проте деякі з них забувають підносити до степеня коефіцієнт.

До основних видів тотожних перетворень многочленів належать: зведення многочленів до стандартного вигляду, додавання і віднімання многочленів, множення одночлена на многочлен і обернене перетворення (розкладання многочлена на множники способом винесення спільного множника за дужки), множення многочлена на многочлен і обернене перетворення (розкладання многочлена на множники способом групування).

Зведення многочлена до стандартного вигляду виконується зведенням подібних членів. Це перетворення фактично відоме учням 5-6 класів. Важливо, щоб учні могли пояснити теоретичну основу цього перетворення і правило його виконання (щоб звести подібні члени, треба додати їх коефіцієнти і приписати до одержаного числа співмножником спільну буквену частину подібних членів).

Додавання і віднімання многочленів являє собою позначення цих дій і зведення подібних членів. При цьому учні повинні добре знати правило розкриття дужок, перед якими стоїть знак «+» або «-».

У курсі алгебри вивчається й обернене перетворення. Тому учні мають знати правило взяття многочлена в дужки, якщо перед ними стоїть знак «+» або «-».

Множення одночлена на многочлен теж фактично відоме учням перетворення з яким вони стикалися в 5-6 класах, вивчаючи    розподільний закон     множення. Труднощі   у сприйманні виникають в окремих учнів під час вивчення оберненого перетворення – розкладання многочленів на множники    способом винесення спільного   множника  за дужки. При вивченні цього тотожного перетворення важливо мотивувати необхідність в ньому.

Тому доцільно сформулювати учням правило розкладання многочленів на множники способом винесення спільного множника за дужки: 1) знайти спільний множник всіх членів многочлена; 2) кожний член многочлена подати у вигляді добутку двох множників, з яких один спільний; 3) винести спільний множник за дужки, спираючись на розподільний закон множення.

Практика свідчить про доцільність виділення спеціального правила відшукання спільного множника членів многочлена. Для цього треба:

1) знайти найбільший спільний дільник всіх коефіцієнтів членів; 2).помножити   його   на степені    змінних  з   найменшим показником, з яким вони входять до всіх членів многочлена. Типовою помилкою, яку учні допускають, виконуючи зазначене тотожне перетворення, є така: учні не ставлять в дужках число 1 замість члена, який збігається зі спільним множником після його винесення за дужки. Тому слід приділити належну увагу завданням такого типу:   18х³ – 12х² + 6х = 6х (3х² – 2х + 1).

Чинна програма передбачає вивчення в 7 класі п'яти формул скороченого множення:

(a + b)² = a²+ 2ab + b² – квадрат суми двох виразів (a – b)² = a²– 2ab + b² – квадрат різниці двох виразів a² – b² = (a – b) (a + b) – різниця квадратів двох виразів a³– b³ = (a – b) (a²– ab + b²) – різниця кубів двох виразів a³ + b³ = (a + b) (a²+ ab + b²) – сума кубів двох виразів Доведення формул скороченого множення не викликає труднощів. Вони виникають у частини учнів під час застосування формул, особливо у зворотному порядку. Запам'ятовуванню формул і їх застосуванню сприяє вміння учнів дати словесне формулювання формули. Перш ніж братися до застосування формул для скороченого множення виразів і виконання оберненого перетворення, треба розв'язати кілька усних вправ на знаходження квадратів одночленів з числовими коефіцієнтами, на запис одночлена у вигляді квадрату одночлена. Система вправ на застосування формул скороченого множення має містити і вправи для усних обчислень.

Наприклад: 51 · 49 = (50 + 1) · (50 – 1) =2 500 – 1 = 2 499;

51² – 49² = (51 + 49) · (51 – 49) = 100 · 2 = 200.

Треба     передбачити  систему вправ     на ефективне використання формул скороченого   множення  до розв'язування     рівнянь, спрощення виразів, доведення тотожностей, виведення формул наближених обчислень.

Під час підсумкового повторення теми «Цілі вирази» доцільно ще раз назвати всі види тотожних перетворень цілих виразів та їх можливі застосування.

3.1. Різні способи розкладання на множники чотиричленів

РОЗКЛАДІТЬ НА МНОЖНИКИ РІЗНИМИ СПОСОБАМИ

𝒂^𝟑−𝒂+𝒂^𝟐−𝟏

Розв’язання

𝒂^𝟑−𝒂+𝒂^𝟐−𝟏

Другий спосіб

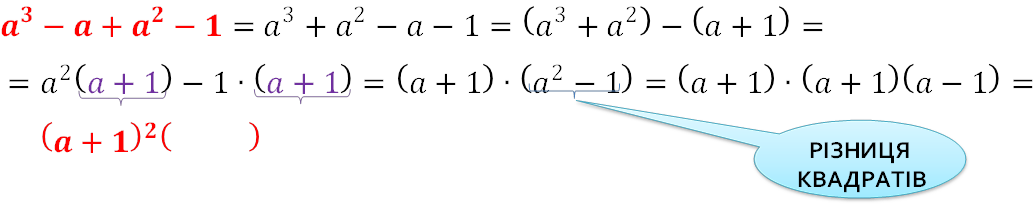=                                                                              𝒂 − 𝟏 .

𝒂^𝟑−𝒂+𝒂^𝟐−𝟏

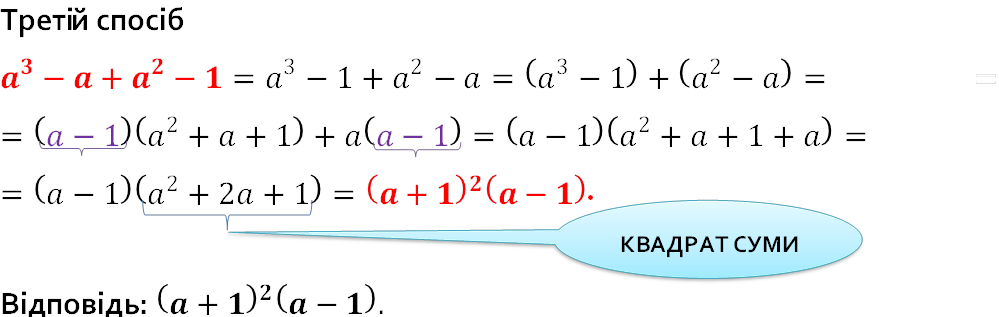
𝒃^𝟐+𝒃^𝟑−𝒃−𝟏

Розв’язання Перший спосіб

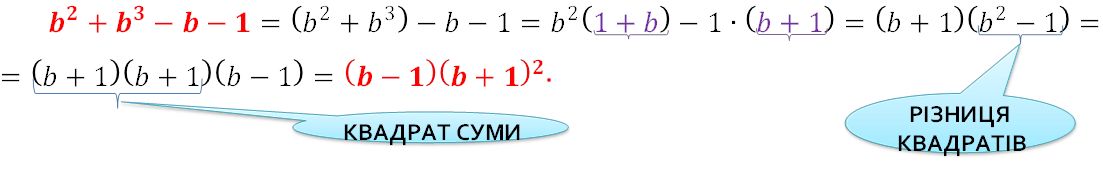
𝒃^𝟐+𝒃^𝟑−𝒃−𝟏

Розв’язання

Другий спосіб

𝒃^𝟐 + 𝒃^𝟑 − 𝒃 − 𝟏 = (𝑏²−𝑏) + (𝑏³−1) = 𝑏 𝑏 − 1

= 𝑏 − 1𝑏 + 𝑏² + 𝑏 + 1 = 𝑏 − 1

𝒃^𝟐+𝒃^𝟑−𝒃−𝟏

Розв’язання Третій спосіб

                                                                                                                                                                            Відповідь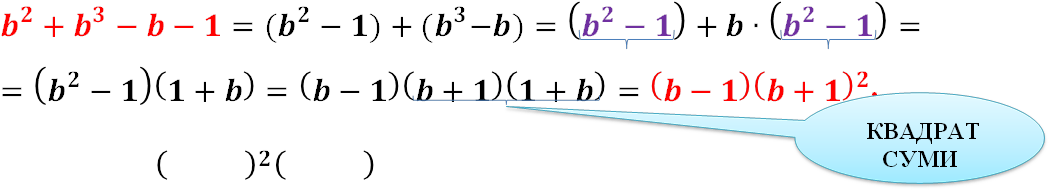: 𝒃 + 𝟏                                                                𝒃 − 𝟏 .

𝒎^𝟓−𝒎^𝟑+𝒎^𝟐−𝟏

Розв’язання

Перший спосіб

𝒎^𝟓 − 𝒎^𝟑 + 𝒎^𝟐 − 𝟏 =𝑚⁵ − 𝑚

=𝑚² − 1𝑚³ + 1=𝑚 − 1

=𝒎 + 𝟏𝒎 − 𝟏𝒎^𝟐 − 𝒎 + 𝟏 .

𝒎^𝟓−𝒎^𝟑+𝒎^𝟐−𝟏

Розв’язання

Другий спосіб

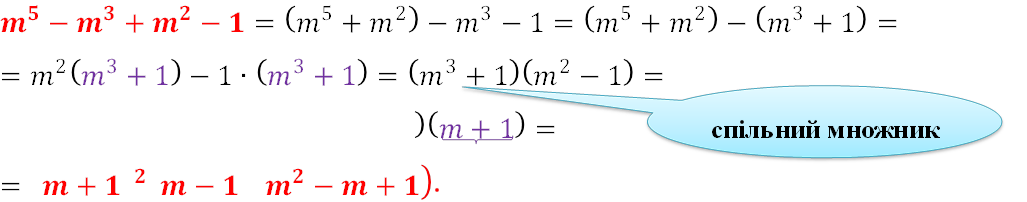                                                                                                                                                                                                                               =                                                                                                          𝑚 + 1                                                                                              𝑚² − 𝑚 + 1                                                                                                                 ∙                                                                                                          𝑚 − 1

𝒎^𝟓−𝒎^𝟑+𝒎^𝟐−𝟏

Розв’язання

	РОЗКЛАДІТЬ НА МНОЖНИКИ РІЗНИМИ
РОЗКЛА		ОБАМИ

Третій спосіб

= 𝑚 − 1 𝑚 + 1 𝑚 + 1 𝑚² − 𝑚 + 1 = 𝒎 + 𝟏                     𝒎 − 𝟏                                                                                             𝒎 − 𝒎 + 𝟏 .

                                                                                                   𝑚⁵ − 1 ∶ 𝑚     − 1 = 𝑚 − 1𝑚⁴ + 𝑚³ + 𝑚² + 𝑚 + 1

𝑚⁵ + 0 ∙ 𝑚⁴ + 0 ∙ 𝑚³ + 0 ∙ 𝑚² + 0 ∙ 𝑚 − 1 𝑚 − 1

𝑚⁴ + 0 ∙ 𝑚³ + 0 ∙ 𝑚² + 0 ∙ 𝑚 − 1

                                                                                                                           𝑚4 −      𝑚3

	РОЗКЛАДІТЬ НА МНОЖНИКИ РІЗНИМИ
РОЗКЛА		ОБАМИ

𝑚³ + 0 ∙ 𝑚² + 0 ∙ 𝑚 − 1

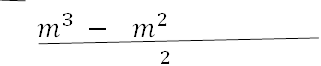                                                                                                                  𝑚 + 0 ∙ 𝑚 − 1                                                                        

𝑚 − 1

0

𝟖𝒕^𝟒−𝟖𝒕^𝟐−𝒕+𝟏

Розв’язання

Перший спосіб

= 𝒕 − 𝟏

= 𝒕 − 𝟏

= 𝒕 − 𝟏

РОЗКЛАДІТЬ НА МНОЖНИКИ РІЗНИМИ СПОСОБАМИ

𝟖𝒕^𝟒−𝟖𝒕^𝟐−𝒕+𝟏

Розв’язання

Другий спосіб

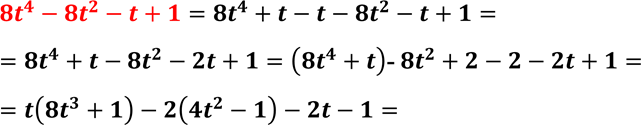
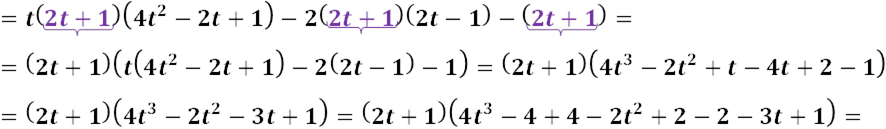
= 𝟐𝒕+𝟏𝟒𝒕^𝟑−𝟒−𝟐𝒕^𝟐+𝟐−𝟑𝒕+𝟑 =

продовження

𝟖𝒕^𝟒−𝟖𝒕^𝟐−𝒕+𝟏

Продовження розв’язання Другий спосіб

                                                                = 𝟐𝒕+𝟏                   𝟒𝒕 −𝟒 − 𝟐𝒕^𝟐−𝟐 − 𝟑𝒕−𝟑 =

= 𝟐𝒕+𝟏 𝟒 𝒕 −𝟏 −𝟐 𝒕^𝟐−𝟏 −𝟑 𝒕−𝟏 =

                                                                 =𝟐𝒕 + 𝟏   𝒕^𝟐 + 𝒕 + 𝟏 − 𝟐 𝒕 − 𝟏 𝒕 + 𝟏 − 𝟑 𝒕 − 𝟏                                       =

                                                                 =𝒕 − 𝟏                                         ^𝟐 + 𝒕 + 𝟏− 𝟑     =

                                                                Відповідь: 𝒕 − 𝟏𝟐𝒕 + 𝟏𝟒𝒕^𝟐 + 𝟐𝒕 − 𝟏.                                                  

3.2. Різні способи розкладання на множники тричленів

РОЗКЛАДІТЬ НА МНОЖНИКИ РІЗНИМИ СПОСОБАМИ

𝒙^𝟐+𝒙−𝟔

Розв’язання

Перший спосіб

𝒙^𝟐 + 𝒙 − 𝟔 = 𝑥²

= (𝑥² +3𝑥) +

                                                               = 𝑥 𝑥 + 3    − 2 𝑥 + 3    =   𝒙 + 𝟑𝒙 − 𝟐.

𝒙^𝟐+𝒙−𝟔

Розв’язання Другий спосіб

𝒙^𝟐 + 𝒙 − 𝟔 = 𝑥²

= 𝑥² − 2𝑥 + 3𝑥 − 6 =

                                                                 = 𝑥 𝑥 − 2    + 3 𝑥 − 2 = 𝒙 + 𝟑𝒙 − 𝟐.

𝒙^𝟐+𝒙−𝟔

Розв’язання

𝒙^𝟐+𝒙−𝟔

Розв’язання

= 𝑥 + 3𝑥 − 3 + 1 = 𝒙 + 𝟑𝒙 − 𝟐.

П′ятий спосіб

^𝟐 + 𝒙 − 𝟔 = 𝑥² + 2 ∙ 𝑥 ∙ 1                      2

𝒙

2

                                           1²             1                                         25

=            𝑥 +− 6          =     𝑥 +

                                                      24                                                   4

𝒙^𝟐+𝒙−𝟔

Розв’язання

              Шостий спосіб    Розв’яжемо рівняння 𝑥² + 𝑥 − 6 = 0.

𝑥² + 𝑥 − 6 = 0.

D >0 (  два різні корені).

За теоремою Вієта :  _ቊ𝑥1 + 𝑥₂ = −1, 𝑥₁ ∙ 𝑥₂ = −6.

Неважко здогадатися, що 𝑥₁ = −3, 𝑥₂= 2.

Тоді одержимо:

                                                                                                          𝒙^𝟐 + 𝒙 − 6 = 1 ∙     𝑥 −  𝑥 − 2 = 𝒙 + 𝟑𝒙 − 𝟐.

Відповідь: 𝒙 + 𝟑

𝟒𝒂^𝟐−𝟏𝟐𝒂+𝟓

Розв’язання Перший спосіб

𝟒𝒂^𝟐 − 𝟏𝟐𝒂 + 𝟓 = 4𝑎² − 2 ∙ 2𝑎 ∙ 3 + 3² − 3² + 5 =

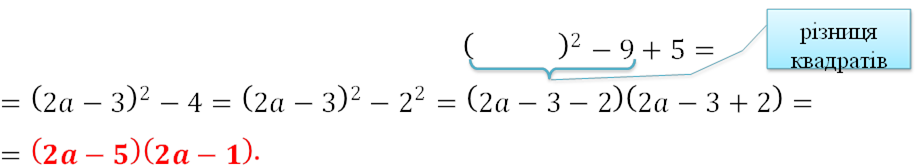= 2𝑎 ² − 2 ∙ 2𝑎 ∙ 3 + 3² − 3² + 5 = 2𝑎 − 3

𝟒𝒂^𝟐−𝟏𝟐𝒂+𝟓

Розв’язання

𝟏𝟐𝒙^𝟐−𝟓𝒙−𝟕

Розв’язанн

Перший спосіб

𝟏𝟐𝒙^𝟐 − 𝟓𝒙 − 𝟕 = 12𝑥² − 12𝑥 + 7𝑥 − 7 =

                                                                                                                                                                                                        =                                                                             12𝑥² − 12𝑥                                                                                      +       7𝑥 − 7

𝟏𝟐𝒙^𝟐−𝟓𝒙−𝟕

Розв’язання Другий спосіб

𝟏𝟐𝒙^𝟐 − 𝟓𝒙 − 𝟕 = 5𝑥

= 5𝑥² − 5𝑥 + 7𝑥²

                                                                    = 5𝑥𝑥 − 1    + 7 𝑥

= 𝑥 − 1

𝟏𝟐𝒙^𝟐−𝟓𝒙−𝟕

Розв’язання Третій спосіб

𝟏𝟐𝒙^𝟐−𝟓𝒙−𝟕

𝟏𝟐𝒙

= 12

= 12

𝟏𝟐𝒙^𝟐−𝟓𝒙−𝟕

Розв’язання

П′ятий спосіб

𝟏𝟐𝒙^𝟐 − 𝟓𝒙 − 𝟕 = 12𝑥² − 5𝑥 − 12 + 5 = 12𝑥² − 12 − 5𝑥 + 5 =

= 12𝑥² − 12 − 5𝑥 − 5

                                          = 12 𝑥 − 1     𝑥 + 1 − 5 𝑥 − 1

                                          = 𝑥 − 1     12𝑥 + 12 − 5 =

Відповідь: 𝒙 − 𝟏𝟏𝟐𝒙 + 𝟕 .

𝒙^𝟐+𝟖𝒙+𝟏𝟐

Розв’язання Перший спосіб

𝒙^𝟐 + 𝟖𝒙 + 𝟏𝟐 = 𝑥

+2𝑥 + 12

𝒙^𝟐+𝟖𝒙+𝟏𝟐

Розв’язання

Другий спосіб

𝒙^𝟐 + 𝟖𝒙 + 𝟏𝟐 = 𝑥²

= 𝑥² + 2𝑥 + 6𝑥 + 12 =

                                                  = 𝑥 𝑥 + 2    + 6 𝑥 + 2 = 𝑥 + 2𝑥 + 6 = 𝒙 + 𝟔𝒙 + 𝟐.

𝒙^𝟐+𝟖𝒙+𝟏𝟐

Розв’язання

Третій спосіб

𝒙^𝟐 + 𝟖𝒙 + 𝟏𝟐 = 𝑥² + 8𝑥 + 16 − 4 =

= 𝑥² − 4 + 8𝑥 + 16 = 𝑥²

                                                 = 𝑥 − 2    𝑥 + 2   + 8 𝑥 + 2 = 𝑥 + 2𝑥 − 2 + 8 =

                                                 = 𝑥 + 2    𝑥 + 6    = 𝒙 + 𝟔    𝒙 + 𝟐.

𝒙^𝟐+𝟖𝒙+𝟏𝟐

Розв’язання

Четвертий спосіб

𝒙^𝟐 + 𝟖𝒙 + 𝟏𝟐 = 𝑥² + 8𝑥 + 48 − 36 =

= 𝑥² − 36 + 8𝑥 + 48 =

                                                 = 𝑥 − 6    𝑥 + 6   + 8 𝑥 + 6

𝒙^𝟐+𝟖𝒙+𝟏𝟐

Розв’язання

П′ятий спосіб

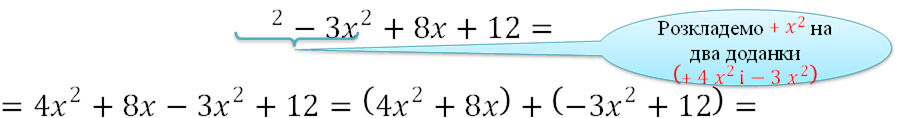𝒙^𝟐 + 𝟖𝒙 + 𝟏𝟐 = 4𝑥

= 4𝑥𝑥 + 2 + −3𝑥² − 4 = 4𝑥𝑥 + 2 − 3 𝑥

                                          = 4𝑥 𝑥 + 2    − 3 𝑥 + 2     𝑥 − 2 = 𝑥 + 2

= 𝑥 + 24𝑥 − 3𝑥 + 6 = 𝑥 + 2𝑥 + 6 = 𝒙 + 𝟔𝒙 + 𝟐.

𝒙^𝟐+𝟖𝒙+𝟏𝟐

Розв’язання

Шостий спосіб

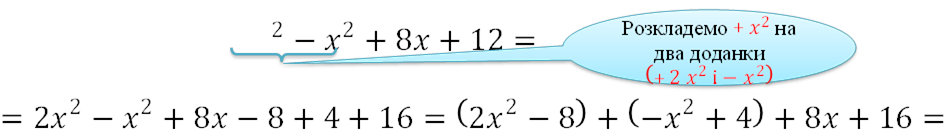𝒙^𝟐 + 𝟖𝒙 + 𝟏𝟐 = 2𝑥

                                                  = 2 𝑥² − 4    −   𝑥² − 4    + 8𝑥 + 2 =    𝑥² − 4               + 8 𝑥 + 2     =    різниця

квадратів

                                                =   𝑥 − 2    𝑥 + 2    + 8 𝑥 + 2 = 𝑥 + 2     𝑥 − 2 + 8      =   𝒙 + 𝟔  𝒙 + 𝟐 .

𝒙^𝟐+𝟖𝒙+𝟏𝟐

Розв’язання

Сьомий спосіб

𝒙^𝟐 + 𝟖𝒙 + 𝟏𝟐 = 𝑥² + 2 ∙ 𝑥 ∙ 4 + 4² − 4² + 12 =

= 𝑥² + 2 ∙ 𝑥 ∙ 4 + 4² − 4² + 12 = 𝑥 + 4² − 16 + 12 =

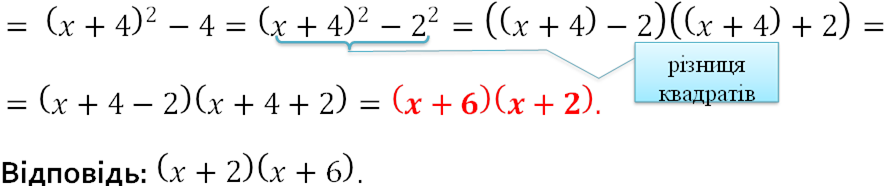
𝒙^𝟐−𝟓𝒙+𝟒

Розв’язання Перший спосіб

𝒙^𝟐−𝟓𝒙+𝟒

Розв’язання

Другий спосіб

𝒙^𝟐−𝟓𝒙+𝟒=𝑥²−4𝑥−𝑥+4=

= 𝑥² − 4𝑥 + −𝑥 + 4

                  = 𝑥 𝑥 − 4    − 1 ∙   𝑥 − 4 = 𝑥 − 4𝑥 − 1 = 𝒙 − 𝟏𝒙 − 𝟒.

𝒙^𝟐−𝟓𝒙+𝟒

Розв’язання Третій спосіб

𝒙^𝟐 − 𝟓𝒙 + 𝟒 = 𝑥²

= 𝑥² − 𝑥 + −4𝑥 + 4

                  = 𝑥 𝑥 − 1    − 4 𝑥 − 1    = 𝒙 − 𝟏𝒙 − 𝟒.

𝒙^𝟐−𝟓𝒙+𝟒

Розв’язання

Четвертий спосіб

𝒙^𝟐 − 𝟓𝒙 + 𝟒 = 𝑥²

= 𝑥² − 1 − 5𝑥 + 5 =

= 𝑥 − 1𝑥 + 1 + −5𝑥 − 1 =                         𝑥 + 1 − 5 𝑥 − 1                                                                               =

= 𝑥 − 1𝑥 + 1 − 5 = 𝒙 − 𝟏

𝒙^𝟐−𝟓𝒙+𝟒

Розв’язання П′ятий спосіб

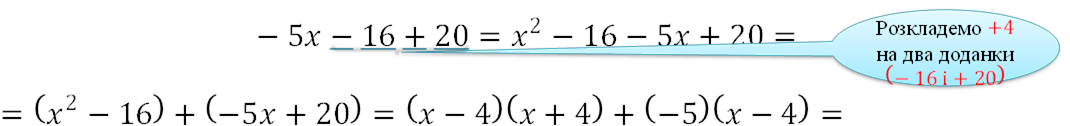𝒙^𝟐 − 𝟓𝒙 + 𝟒 = 𝑥²

=    𝑥 − 4     𝑥 + 4 − 5 𝑥 − 4   = 𝑥 − 4𝑥 + 4 − 5 =

=    𝑥 − 4    𝑥 − 1 =    𝒙 − 𝟏    𝒙 − 𝟒.

𝒙^𝟐−𝟓𝒙+𝟒

Розв’язання Шостий спосіб

2

9

−  =

4

3

+=

2

=

ВИСНОВКИ

Підсумовуючи, ще раз наголосимо, що для усунення формалізму в засвоєнні навичок і вмінь виконання тотожних перетворень різних виразів треба поряд із введенням основного завдання перетворення (зведення до стандартного вигляду) домагатися усвідомлення учнями того, що у кожному конкретному випадку метою тотожних перетворень є подання виразу у вигляді, зручному для розв’язування поставленої задачі.

ВИСНОВКИ

Культура виконання тотожних перетворень розвивається на підставі міцних знань властивостей операцій та алгоритмів їх виконання. Культура виявляється не тільки в умінні правильно обґрунтовувати перетворення, але й у вмінні знайти найкоротший шлях переходу від даного виразу – до потрібного, в умінні простежити за зміненням області визначення виразу, у швидкості і безпомилковості виконання перетворення.

Список використаної літератури:                                              

1.      Алферов О. Д. Формування відповідального ставлення до навчання : навч. посіб. / О. Д. Алферов. – М., 1984. - 69 с.

2.      Баженюк З. С. Діагностика особливостей мотивації навчальної діяльності школярів підліткового віку / З. С. Баженюк // Методичні рекомендації. – Луцьк, 1999. - С. 2-17.

3.      Бевз В. Г. Практикум з історії математики: Навч. посіб. для студентів фіз.-мат. ф -тів. // В. Г. Бевз. – К. : НПУ імені М. П. Драгоманова, 2008. - 312 с.

4.      Бевз В.Г. Уроки математики в 6 класі : Кн. для вчителя / В.Г. Бевз, Г.П Бевз. – К. : Генеза, 2007. - 240 с.

5.      Бевз Г. П. Методика викладання математики [5]/ Г. П. Бевз // Київ "Вища школа". – 1989. – Режим доступу до ресурсу: https://edu-lib.com/matematika-2/dlya-studentov/bevz-gp-metodikavikladannya-matemati.

6.      Бевз Г. П., Бевз В. Г. Алгебра: Підруч. для 7 кл. загальноосвіт. навч. закл. – К.: Зодіак – ЕКО, 2007. – 304 с.

7.      Буйницька О. П. Інформаційні технології та технічні засоби навчання: навч. посіб. / О.П. Буйницька; М-во освіти і науки, молоді та спорту України, Київ. ун-т ім. Б.Грінченка. – К. : Центр уч. літ., 2012. - 240 с.

8.      Бурда М. І., Кудренко Б. В.. Навчальні програми для 5-9 класів, 2017 рік. Математика. – Режим доступу до ресурсу: https://mon.gov.ua/ua/osvita/zagalna-serednya-osvita/navchalniprogrami/navchalni-programi-5-9-klas.

9.      Вишенський В.А., Перестюк М.О., Самойленко А.М. Збірник задач з математики: Навч. посібник. - 2-ге вид., доп. — К.: Либідь, 1993. - 344 с.

10.                       Котловська О. Використання міжпредметних зв’язків на уроках математики / Олена Котловська, Лариса Вязнінова, Юлія Андрух // Математика. — 2013. - № 3. - С. 3-7.

11.                       Кравчук В., Янченко Г. Алгебра: Підручник для 7 класу. – Т: 2007. – 224 с.

12.                       Кузьмінський А. І. Наукові засади методичної підготовки майбутнього вчителя математики : [монографія] / А. І. Кузьмінський, Н. А. Тарасенкова, І. А. Акуленко. – Черкаси : Вид. від. ЧНУ ім. Б. Хмельницького, 2009. – 320 с.

13.                       Лященко Є. І., Зобкова К. В., Кириченко Т. Ф. Лабораторные и практические работы по методике преподования математики під ред. Є. І. Лященко. – М.: Просвещение, 1988. – 223 с.

14.                       Маркова А. К. Проблеми формування мотиваційної навчальної діяльності / А. К. Маркова. — К., 1989. - 57 с.

15.                       Мордкович А.Г. Алгебра. 7 кл.: Учеб. для общеобраэоват. учреждений. — 4-е изд., испр. — М.: Мнемозина, 2001. — 160 с.

16.                       Моторіна В. Г. Технології навчання математики в сучасній школі. — Х: 2001, 262 с.

17.                       Прокопенко Н.С. Програма для загальноосвітніх навчальних закладів з математики 5-12 класи. Міністерство освіти і науки України, 2005. ВТФ «Перун».

18.                       Рогановский Н. М. Методика преподования математики в средней школе: Учебн. Пособие. — Мн.: Выш. Шк., 1990. – 267 с.

19.                       Саушкін О.Ф. Розв’язування алгебраїчних рівнянь. — К.: КНЕУ.

20.                       Слєпкань Г. А. Методика викладання математики / Г. А. Слєпкань. – 2000. – Режим доступу до ресурсу: https://edu-lib.com/izbrannoe/slyepkan-z-i-metodikanavchannya-matema.

21.                       Слєпкань З. І. Методика навчання математики: Підручник. – 2-ге вид., допов. і переробл. — К.: Вища шк., 2006. – 582 с.

22.                       Сухомлинський В. О. Вибрані твори : у 5 т. Т. 2 : Як виховати справжню людину. Сто порад вчителеві. — К. : Рад. шк., 1976. - 670 с.

23.                       Таран Н. В. психолого-педагогічні основи застосування індивідуального підходу до навчання / Ніна Володимирівна Таран. – 2018. – Режим доступу до ресурсу: https://vseosvita.ua/library/psihologo-pedagogicni-osnovi-zastosuvannaindividualnogopidhodu-v-navcanni-molodsih-skolariv-53702.html.

24.                       Тарасенкова Н. А. Використання знаково-символічних засобів у навчанні математики : [монографія] / Н. А. Тарасенкова. – Черкаси : «Відлуння-Плюс», 2002. – 400 с.

25.                       Тарасенкова Н. А. Організація навчально-виховного процесу в багатопрофільній школі : [монографія] / Н. А. Тарасенкова, І. А. Акуленко, І. В. Лов’янова, А. Й. Жгир, Б. Й. Окунєв та ін. – Черкаси : [б. в.], 2013. – 272 с.

26.                       Тарасенкова Н. А. Структура і зміст навчально-методичного комплекту з алгебри для 7 класу / Тарасенкова, І. М. Богатирьова, О. М. Коломієць, З. О. Сердюк // Science and education a new dimension. – ІІІ (26), Issue: 50. – Budapest: SCASPEE, 2015. – P. 12-18.

27.                       Тарасенкова Н. А. Навчальні програми для загальноосвітніх навчальних закладів : Математика; Інформатика. 5-9 класи. – К. : Видавничий дім «Освіта», 2013. - 96 с.

28.                       Чайковський М.А. Квадратні рівняння. — К., 1970. - 242 с.

29.                       Шарко В. Д. Сучасний урок : технологічний аспект / В. Д. Шарко. — К, : Фенікс, - 2006. 223 с.