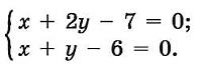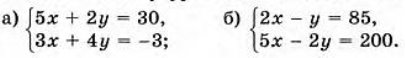Урок. "Основи роботи в середовищі Scilab. Розв’язування рівнянь, систем рівнянь в середовищі Scilab. Розв’язування задач із різних предметних галузей. "

 

Урок 7            10 клас

 

Тема. Основи роботи в середовищі Scilab. Розв’язування рівнянь, систем  рівнянь в середовищі Scilab. Розв’язування задач із різних предметних галузей.

Тип М-М10: Адаптивно-перетворювальний

Мета:

Розуміння призначення середовища Scilab, уміння аналізувати інформацію у вікнах середовища, пояснювати синтаксис і семантику команд, визначити типи констант і змінних, які використовуються в командах; уміння використовувати правила запису виразів; уміння задавати значення змінних різних типів; уміння визначити результати арифметичних виразів і вбудованих функцій.

 

Компетентності:

• Математична: уміння записувати арифметичні вирази, користуватися вбудованими математичними і синтаксичними функціями);
• Інформаційна-комунікативна: уміння вести діалог «людина-технічна система», вміння коректно добирати типи даних для розв’язування задачі, вміння порівнювати  можливості різних програмних засобів для розв’язування обчислювальних завдань;
• Навчання впродовж життя: уміння користуватися довідковою системою програмного середовища;
• Громадянські та соціальні: свідоме дотримання вимог користування ліцензованим або вільним програмним забезпеченням.

 

Очікувані результати: учні повинні вміти вводити команди, отримувати та правильно інтерпретувати результати, виконувати обчислення виразів у середовищі Scilab.

 

Обладнання: зошит-конспект, ПК зі встановленим пакетом Scilab .

 

Хід уроку:

1. Організаційний етап
2. Рефлексія

Перевірка д/з.

Актуалізація опорних знань: повторити поняття ідентифікатор, тип величини, вид величини, значення величини, оголошення змінних, оператор присвоєння.

3. Усна підготовка

Мотивація: для виконання інженерних і наукових обчислень та налізу даних існують спеціальні програмні засоби – системи комп’ютерної математики. Одним із них є пакет Scilab  - вільне це вільне багато платформне програмне забезпечення з відкритим вихідним кодом. Сьогодні на уроці ми розглянемо середовище програми Scilab та способи розв’язання різних математичних задач за допомоги цієї програми.

4. Робота за темою

 

Знайомство з інтерфейсом

 

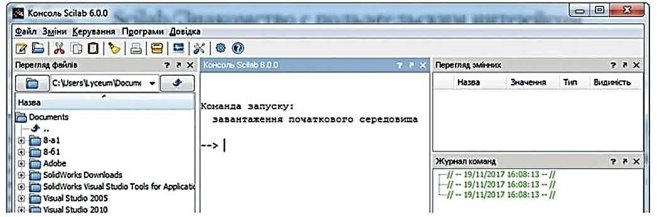
    Головне вікно Scilab містить чотири основні вікна: 

• Перегляд файлів; 
• Командне вікно (Консоль); 
• Перегляд змінних; 
• Журнал команд.

 

    У Командному вікні (Консоль) можна спостерігати технічну інформацію про завантаження середовища, після якої система запрошує користувача ввести команду. Початок рядка супроводжується стрілкою (-->), яка й на­зивається запрошенням (command prompt). Середовище працює в режимі інтерпретатора (здійснює пооператорну (покомандну, построкову) обробку команд). 

    Якщо ввести рядок 

-->2*2+69/25 ,
отримаємо відповідь від інтерпретатора: 

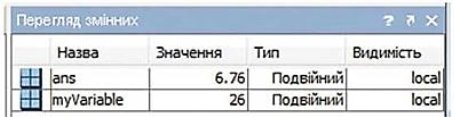
ans = 6.76 
    Змінна ans — це зарезервована змінна, в яку зберігається останній «безіменний» результат. Змінна ans може бути використана для прове­дення ланцюжка обчислень, проміжні результати яких вам не потрібні:

-->2*2

ans = 4. 

-->ans+4 

ans = 8. 

    У вікні Перегляд змінних ві­дображається інформація про створені змінні. 

 

 

    Вікно Журнал команд відображає всі команди, які вводив користувач у командний рядок під час поточного сеансу. Сеансом називається відрі­зок часу, що починається з уведення першої команди після запуску про­грами, і закінчується закриттям програми.

    

Правила введення інформації в документ 

    1) Якщо не потрібно виводити результат, то введення інформації закінчується символом «;». Водночас самі обчислення викону­ються. Тому, якщо запам'ятовувати результати в змінних, то за потреби з ними в подальшому можна буде виконувати операції. 
    2) В одному рядку можна ввести кілька операторів і (або) команд. Для цього їх слід відокремлювати символом «,»:

-->2+3, 3+5 

ans = 5 

ans =8 // змінна ans містить результат обчислення останнього виразу. 

    3) Якщо вираз не поміщається в рядку, то наприкінці незаверше­ного рядка слід увести дві крапки «..». 
    4) Переглянути раніше введені команди можна в командному ряд­ку за допомогою клавіш управління курсором «угору» й «униз». Отримавши доступ до потрібної команди, її можна змінити й зно­ву запустити на виконання. 
    5) Видалення фрагмента документа, крім тексту, що міститься в ко­мандному рядку, системою не дозволяється.

 

Типи даних

    У робочій області Scіlab можна визначати змінні, а потім використо­вувати їх у виразах. Змінна в Scіlab – це іменований масив лише з одним полем, яке зберігає дані деякого типу. Будь-яка змінна до викорис­тання у формулах і виразах має бути визначена. Для визначення змінної необхідно записати оператор присвоювання

ім'я_змінної = значення    

    Наберемо в командному вікні рядок: 

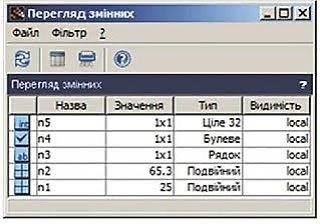
-->n1=25; n2=65.3; n3="text"; n4=%T; n5=int32(10);
    Тим самим ми створили 5 змінних, інформацію про значення й типи яких можна переглянути у вікні Перегляд змінних. 

 

 

    Убудований цілий тип у Scіlab від­сутній, тому ціле значення отриму­ємо за допомогою функції перетво­рення типів int32(). Змінна n4 має логічний тип і значення %Т, еквіва­лентне True (%F ~False). 
    Вектор у Scіlab — це одновіимірний масив одного типу даних. Нумерація елементів починається з одиниці. Для створення вектора необ­хідно перелічити елементи через пропуск у квадратних дужках: 

Vector = [3 6 8]; // Вектор із 3 елементами 

    Для створення вектора, елементи якого утворюють арифметичну про­гресію, використовується конструкція 

<Початкове значення:> <крок>: <кінцеве значення> 

     Приклад 1. Створимо вектор із початковим значенням -5, кінцевим значенням 10 і кроком між елементами 2. 

-->А=-5:2:10 

А = - 5. -3. -1. 1. 3. 5. 7. 9. 

-->А(4) // Звернення до елемента вектора А з індексом 4 

ans = 1.

    Для видалення елемента вектора достатньо на його позиції записати конструкцію «[ ]». 

    -->А(2)=[ ] // Видалено елемент А(2) 

А = -5. -1. 1. 3. 5. 7. 9.

 

    Матриця в Scilab — це двовимірний масив однотипних елементів.  У разі створення матриці рядки відділяються крапкою з комою: 

-->А=[1 2; 3 4] // створення матриці 2x2 

 

А =    1. 2. 

          3. 4. 

      Приклад 2. Для створення матриці можна скористатися стандартною функцією rand(), яка генерує масиви, заповнюючи їх псевдовипадковими числами. 

-->A=rand(2,3) // створення матриці 2x3

 

А =  0.2113249      0.6653811      0.8782165

        0.7560439      0.6283918      0.0683740

 

    Звернемося до елемента, розташованого в другому рядку й третьому стовпці: 

 

-->А(2,3) // 2 рядок, 3 стовпець 

ans = 0.0683740

   

Правила запису виразів

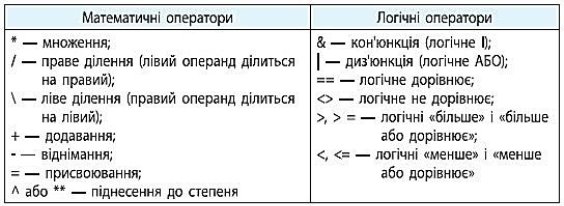
    Математичні вирази складаються з чисел, констант, змінних, операто­рів, функцій і спеціальних знаків. Порядок дій регулюється дужками. Ви вже знаєте основні оператори, які використовуються для запису виразів:

 

 

Вбудовані функції

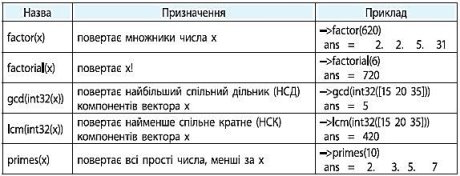
    Для запису математичних виразів використовуються елементарні ма­тематичні функції:

 

     Приклад 3. Обчислити значення виразу 

,

якщо х = 4.5, у = 8.09. 

 

-->х= - 4.5; у=8.09; 

-->с=sqrt(abs(x^2-1))+sin(x)^2

с = 5.3430473 

    

    Для розв'язування задач теорії чисел і комбінаторики реалізовані вбудовані функції:

 

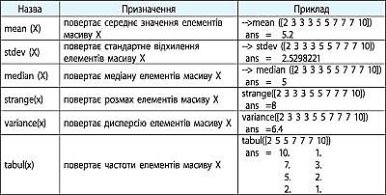
    Scіlab має вбудовані функції для статистичної обробки даних:

 

 

    Якщо ви не впевнені в призначенні вбудованої функції або її синтак­сисі, скористайтеся командою help, наприклад:

--> help factor 

    У результаті виконання команди у вікні Перегляд довідки буде відо­бражено інформацію щодо цієї функції.

 

Тип М-М11: системно-узагальнюючий

Мета:

Розуміння поняття «об’єкт» ; уміння аналізувати інформацію у вікнах середовища, пояснювати синтаксис і семантику команд створення і обчислення полінома; уміння пояснювати алгоритм розв’язування системи  лінійних алгебраїчних рівнянь; уміння пояснювати схему роботи в програмному режимі, розуміння поняття і правила опису функції користувача; уміння пояснювати алгоритм обчислення похідної функції.

 

Компетентності:

• Математична: уміння застосовувати методи розв’язування рівнянь, систем рівнянь обчислення похідної функції;
• Компетентності у галузі природничих наук, техніки і технологій: уміння обирати оптимальне програмне середовище для розв’язування обчислювальних задач;
• Інформаційна-комунікативна: уміння вести діалог «людина-технічна система», вміння коректно зберігати та редагувати програмний код, вміння порівнювати  можливості різних програмних засобів для розв’язування обчислювальних завдань;
• Навчання впродовж життя: уміння оцінювати достовірність і точність отриманих результатів;
• Громадянські та соціальні: готовність до співпраці у процесі створення програм (розробка, опис, налаштування, тестування) та аналізу результатів їх роботи.

 

Очікувані результати: учні повинні вміти обчислювати значення полінома, розв’язувати рівняння і системи алгебраїчних рівнянь, створювати зберігати й виконувати сценарії Scilab, зберігати у файоах описи функцій користувача.

 

Обладнання: зошит-конспект, ПК зі встановленим пакетом Scilab .

 

Хід уроку

1. Організаційний момент
2. Сприйняття і усвідомлення матеріалу

 

Розв’язування рівнянь, систем рівнянь в середовищі Scilab

    Об’єкти — вбудовані типи даних, які є основою для проведення математичних розрахунків. Внутрішня структура об'єктів прихована від очей користувачів. Роботу з пам'яттю під час обробки об'єктів середовище також бере на себе. В основі своїй об'єкти є масивами, у яких збережені певні дані.

 

Об’єкт Поліном 

    Прикладом об’єкта є поліном. З алгебри ви знаєте, що поліномом на­зивають алгебраїчне рівняння виду:

 

    Поліном задається функцією poly():

     poly(a,vname,'c'), 

де а — масив коефіцієнтів; 
    vname — ім’я символьної змінної (невідомий член); 
    'с' — прапорець, який визначає, що коефіцієнти полінома формуються зі значень, наведених у масиві а. 

    Приклад 1: Уведемо поліном другого порядка з коефіцієнтами -10, 4, 2. 

    -->p=poly([-10 4 2],'х','с') 

    р = - 10 + 4х + 2x2

 

    Для пошуку коренів полінома в Scilab є функція roots(<iм'я полінома>). 

    Приклад 2. Знайти корені квадратного рівняння -10 + 4х + 2х²=0. 

    -->R=roots(p) 
     R = 
         -3.4494897 

         1.4494897

 

Розв’язування системи лінійних алгебраїчних рівнянь

    Scilab дає змогу розв’язувати системи лінійних алгебраїчних рівнянь виду Ах = b. У документі для значень А формується двовимірна матриця коефіцієнтів при невідомих, кожен рядок якої містить коефіцієнти одно­го рівняння, а для значень b формується вектор із вільних коефіцієнтів. 

    Після цього для розв’язування системи використовується функція linsolve, що має такий синтаксис: 

[X] = linsolve (А, b) 

 

де А — це матриця коефіцієнтів при невідомих, b — вектор вільних коефіцієнтів. 
    Функція повертає знайдені значення невідомих системи у вигляді масиву. 

    Приклад 3.  Розв’язати систему лінійних рівнянь:

 

    --> А=[1 2; 1 1]; b=[-7;-6]; 
    --> x=linsolve(A,b)

      x = 
            5. 
            1. 
    Шукані значення: х₁ = 5, х₂ = 1. 
    Якщо система не має розв’язків, то видається повідомлення "WARNING: Conflicting linear constraints!" (Конфліктуючі умови для лінійних рівнянь). 
    Якщо система має множину розв’язків, то функція повертає тільки один розв’язок. 

 

Функції користувача 

    Окрім вбудованих, ви можете використовувати власні функції, попе­редньо описавши їх за допомогою конструкції function...endfunction:

 

    function <результат функції>=ім'я_функції(аргументи) 
        <інструкції> 
    endfunction 

    Приклад 4. Описати функцію у = х²: 

        -->function y=f(x) 
        -->у=х^2 

        -->endfunction 

    Далі ви можете викликати цю функцію для обчислення її значення І для різних аргументів: 

        -->f(4) 

        ans = 16. 

    Функції користувача можна зберігати у файлах із розширенням .sci. 

    Обчислення похідної функції 

    У курсі алгебри 10 класу ви вивчаєте поняття похідної функції. Зна­йти значення похідної функції f у точці х можна за допомогою функції numderivative (f, х). 

    Приклад 5. Обчислити похідну функції f(x) = (х + З)² + 5, якщо х = 1. 

        -->function f=myfun(x) 
        -->f=(x+3)^2 + 5

        -->endfunction 

        -->x=1; 
        -->g=numderivative (myfun, x) 

        g = 8. 

 

    Навіть первинне знайомство з середовищем розкриває потужні мож­ливості пакета для розв’язування рівнянь і систем рівнянь. До того ж система має власну мову програмування високого рівня, що дає користу­вачеві змогу створити нову функцію й використовувати її нарівні зі вбу­дованими.

 

Тип М-М12: контрольно-рефлексивний

Мета:

уміння пояснювати синтаксис і семантику команд обчислення функцій моди, медіани, середнього значення, стандартного відхилення;.

Компетентності:

• Математична: уміння обчислювати функції моди, медіани, середнього значення, стандартного відхилення;
• Компетентності у галузі природничих наук, техніки і технологій: уміння обирати оптимальне програмне середовище для розв’язування обчислювальних задач;
• Інформаційна-комунікативна: уміння вести діалог «людина-технічна система», вміння порівнювати  можливості різних програмних засобів для розв’язування обчислювальних завдань;
• Навчання впродовж життя: уміння користуватись довідковою системою програмного середовища;

 

Очікувані результати: учні повинні вміти обчислювати моду, медіану, середнього значення, стандартного відхилення в середовищі Scilab.

 

Обладнання: зошит-конспект, ПК зі встановленим пакетом Scilab .

 

Хід уроку

 

1. Організаційний етап
2. Повідомлення теми і мети

Тема: вирішення оптимізаційної задачі в програмному середовищі Scilab  та MS Excel.

Мета: навчитися обчислювати моду, стандартне відхилення, медіану та середня значення за допомогою Scilab , а також порівняння результатів та алгоритму обчислення цих функцій з табличним процесором MS Excel.

3. Виконання практичної роботи

Робота за комп’ютером

 

Практична робота №3

 

    Завдання. У таблиці наведено витрати студента на обіди в їдальні протягом тижня: 

 

 

Методичні вказівки:

    1. Завантажте середовище Scilab. У командному вікні наберіть і ви­конайте команду створення вектора значень витрат: 

 

v = [32 40 32 50 30 40 50]; 

    Проаналізуйте, яку інформацію щодо змінної v відображено у вік­ні Перегляд змінних. 
    2. Обчисліть частоти елементів масиву v. 
    3. Обчисліть середнє значення вартості обіду. 
    4. Обчисліть медіану, розмах і стандартне відхилення еле­ментів масиву v. 
    5. Створіть нову книгу MS Excel (LO Calc) і занесіть на аркуш дані таблиці. Обчисліть частоти, середнє значення, медіану, розмах, дисперсію, стандартне відхилення значень витрат. Порівняйте результати обчислення статистичних характеристик сукупності значень у Scilab і MS Excel (LO Calc).

Дійдіть висновків.

 

   Домашнє завдання

    Завдання 1. Який результат буде виведено після виконання послідовності ко­манд: 

 

    -->p=poly([1 -5],'x','c'); 
    -->R=roots(p)

 

    Завдання 2. Який результат буде виведено після виконання послідовності ко­манд: 

 

    а) -->p=poly([36 12 1],'х','с')                  б) -->p=poly([0.25 -1 1],'х','с')      

               

  в) -->p=poly([16 -14 3],'х','с')

        -->R=roots(p)                                               -->R=roots(p)                                                   -->R=roots(p)

 

Завдання 3. Засобами середовища Scilab розв'яжіть рівняння:

 

 

    Завдання 4. Який результат буде виведено після виконання послідовності команд: 

    --> А=[3 2; 1 1]; b=[7; 4]; 

    --> x=linsolve(A,b)

 

    Завдання 5. Засобами середовища Scilab розв'яжіть системи рівнянь:

 

 

    Завдання 6. Засобами середовища Scilab обчисліть похідну функції  f(x)=x² -3x, якщо х= -1