Урок "Прямокутний паралелепіпед"

Урок №70-71                                                                                                                   Дата__________

Тема : Прямокутний паралелепіпед.

Мета: познайомити учнів з фігурою прямокутний паралелепіпед, його основними елементами. Безпосередніми вимірюваннями та обчисленнями переконатися в справедливості формул для об’єму  прямокутного паралелепіпеда ; розвивати вміння робити обчислення за формулами; виховувати культуру математичних записів, працювати в групах.

Обладнання: мультимедійний проектор, моделі прямокутних паралелепіпедів.

План уроку

1. Оргмомент
2. Повідомлення теми і мети уроку
3. Вивчення нового матеріалу
4. Робота в групах
5. Виконання лабораторно-практичної роботи
6. Підсумок уроку
7. Домашнє завдання

Хід уроку

Розкажи – і я забуду

Покажи – і я запам’ятаю

Дай спробувати – і я зрозумію

(Китайська мудрість)

1.Оргмомент

Перевірка домашнього завдання

 Получилось «Геометричні фігури»

 Які геометричні фігури ми вивчали?

Як знайти периметр прямокутника, квадрата?

Як знайти площу прямокутника, квадрата?

2. Повідомлення теми і мети уроку

Сьогодні на уроці ми познайомимось ще з однією фігурою,її елементами, навчимось знаходити її площу, периметр і об’єм . Тема нашого уроку «Прямокутний пралелепіпед»(сл. 1, 2)

3. Вивчення нового матеріалу

Погляньте на ці предмети-всі вони мають форму прямокутного паралелепіпеда.

Які ще приклади цієї фігури ви можете навести?

Познайомимося з цією фігурою ближче.

KFMHABCD- прямокутний паралелепіпед. Побудуємо його.

Точки А, B, C, D, …-вершини(сл. 3) Скільки вершин?

Відрізки АВ, ВС,СМ, … - ребра (сл. 4) Скільки ребер?

Довжина, ширина, висота – основні виміри прямокутного паралелепіпеда.

Прямокутники – грані (сл. 5) Скільки граней?

Протилежні грані- рівні!

Довжина ребер- це сума довжин всіх ребер прямокутного паралелепіпеда і обчислюється за формулою L=4(a+b+h) (сл. 6) Усно  виконати завдання

Площа поверхні – це сума всіх площ граней і обчислюється за формулою S=2(ab+bh+ah)(сл. 7)

Усно  виконати завдання

Приклад 1.(сл. 8)

Обчислити загальну  довжину всіх ребер і площу поверхні прямокутного паралелепіпеда, якщо його виміри 10см, 5см, 4см.

L =4  (10+5+4) =76 (см)

S = 2  (10  5 + 10  4 + 5   4) =220 (см²)

Приклад 2.(сл9)

З 8 однакових кубиків зі стороною 1 см будують  прямокутні паралелепіпеди. Зобразіть з кубиків всі можливі варіанти. Який з паралелепіпедів      має найменшу площу?

Перевірка (сл. 10)

S = (2*  2) * 6 = 24  (см²

S= (8  *1)  * 4 + (1*  1) * 2 =34 (см²⁾

S= (2 * 4) * 2 + (1*  4)*  2 + ( 2 * 1) * 2 = 28(см²⁾

Розгортка пр. парал має вигляд (сл. 11)

Приклад 3.(сл12)

Які з фігур можуть бути розгортками прямокутного паралелепіпеда?

Куб-прямокутний паралелепіпед, у якого всі виміри рівні (сл13)

 Якими геометричними фігурами являються грані куба?

L=12a-довжина всіх ребер куба

S=6*a²  - площа поверхні куба

Приклад (усно)

а= 3 см. Знайти L,S.

Об’єм прямокутного паралелепіпеда (сл. 14)

1 ряд :

4 x 5 = 20 ( см³)

2 ряд?

4 x 5 = 20 (см³)

3 ряд?

4 x 5 = 20 (см³)

Всього:   4 x 5 x 3 = 60 (см³)

V=a b h

    Одиниця вимірювання об’єму – куб зі стороною 1 (сл15)

V = 1 од³

1 мм³  ,  1 см³,  1 дм³ ,1 км³

Співідношення між одиницями вимірювання величин. (сл. 16)

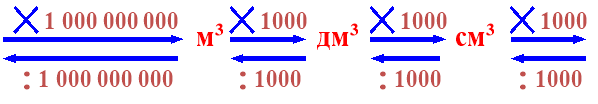
Приклад 4.(сл. 17)

Знайти об’єм прямокутного паралелепіпеда, якщо його виміри          6см, 3см, 4см.

V = a b h;

 V = 6 * 3 * 4 = 72 (см³ )

4. Робота в групах

Знайти об’єм фiгур  (сл. 18)  (5 -7хв)

Перевірка (сл. 19)

5. Лабораторно-практична робота(сл20)

Кожна група одержує моделі прямокутного паралелепіпеда. Учням потрібно виконати наступне:

1) Виміряти три виміри прямокутного паралелепіпеда.

2)Знайти площу основи( S_осн =ab)

3)Знайти добуток площі основи та висоти прямокутного паралелепіпеда

4)Знайти об'єм прямокутного паралелепіпеда

5)Заповнити таблицю

6) Зробити висновок

 Виконати завдання (сл21)

1) Використовуючи  формулу V = S_осн. · h, знайдіть невідому величину (усно)

2) Виразити в м³:

а) 2000 дм³ =

б) 130 000 000 см³ =

в) 297 км³ =

Перевірка (сл21)

6.Підсумок уроку (сл23)

Показати моделі прямокутника і прямокутного паралелепіпеда.

Що це за фігури?

Що спільного у них?

Як називаються у прямокутного паралелепіпеда точки, відрізки, прямокутники? (показати на моделі)

Скільки їх?

Що можна обчислити, знаючи довжину , ширину і висоту ?

7. Домашнє завдання

П. 21, ст. 150-152( опрацюв), виконати № 614, №615, №621, №627