Урок "Розміщення двох площин у просторі"

Тема. Розміщення двох площин у просторі: площини, що перетинаються; паралельні площини. Ознака паралельності площин.

Мета: сформувати в учнів уявлення про взаємне розміщення двох площин у просторі, про паралельні площини й ознаку паралельності двох площин; сформувати вміння застосовувати ознаку паралельності площин при розв’язуванні задач.

Тип уроку: засвоєння нових знань, формування вмінь.

Обладнання: креслярські інструменти, модель прямокутного паралелепіпеда.

Література:

• Для вчителя:

1. Бевз Г.П. Геометрія: підручник для 10 кл. – К.: Генеза, 2010. – 248 с.
2. Математика. Комплексне видання: Довідник з математики. 5 – 11 класи. Аналіз найпоширеніших помилок. Тестові завдання/ О.С. Будна, С.М. Будна, А.Р. Гальперіна, М.Я. Забєлишенська, О.Я Михеєва. – Х.: «Літера» ЛТД, 2009. – 320 с.

• Для учнів:

1. Бевз Г.П. Геометрія: підручник для 10 кл. – К.: Генеза, 2010. – 248 с.

Структура уроку

1. Організаційний етап        (2 хв.)
2. Перевірка домашнього завдання      (10хв.)
3. Актуалізація опорних знань       (5хв.)
4. Вивчення нового матеріалу       (20хв.)
5. Засвоєння вмінь та навичок       (35хв.)
6. Підбиття підсумків уроку       (6хв.)
7. Домашнє завдання        (2хв.)

Хід уроку.

1.                      Організаційний етап.

Проконтролювати, щоб клас провітрили, підготували дошку для уроку. Перевірка готовності учнів до уроку, налаштування їх на роботу.

2.                      Перевірка домашнього завдання.
3.                      Актуалізація опорних знань.

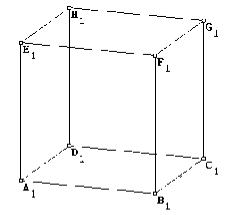
У кубі назвіть площину паралельну:

1.               ;
2.               ;
3.               ;

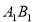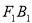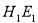4.                      Вивчення нового матеріалу.

План

1.               Взаємне розміщення двох площин.
2.               Означення паралельних площин.
3.               Ознака паралельності площин.

Дві площини в просторі

перетинаються по прямій   не мають спільних точок

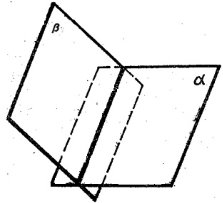
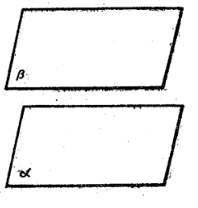
Дві площини називаються паралельними, якщо вони не перетинаються.

Якщо площини і паралельні, то пишуть .

На моделі прямокутного паралелепіпеда демонструю паралельні площини, і площини, що перетинаються.

В навколишньому просторі прикладом паралельних площин є розміщення протилежних стін кімнати.

Теорема (ознака паралельності площин).

Якщо дві прямі, що перетинаються і лежать в одній площині, паралельні двом прямим другої площини, то такі площини паралельні.

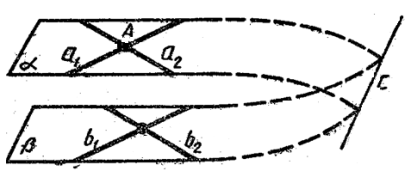
Доведення.

Нехай і - дані площини, і - дві прямі у площині , які перетинаються у точці , і - відповідно паралельні їм прямі у площині . Припустимо, що площини і не паралельні, тобто перетинаються по деякій прямій .

За теоремою (що якщо пряма, яка не належить площині, паралельна якій-небудь прямій у цій площині, то вона паралельна і самій площині) прямі і , як паралельні прямим і , паралельні площині , і тому вони не перетинають пряму , яка лежить у цій площині.

Таким чином, у площині через точку проходять дві прямі ( і ), паралельні прямій .

Але це неможливо за аксіомою паралельності.

Ми прийшли до суперечності. Теорему доведено.

5.                      Засвоєння вмінь та навичок.

1.               У кубі назвіть площину, паралельну:

а) площині ;

б) площині ;

в) площині , де - середина , - середина ; - середина ;

2.               Визначте, чи паралельні площини:

а) і ;

б) і ;

в) і ;

3.               Доведіть, що через дві мимобіжні прямі можна провести паралельні площини.

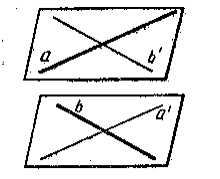
Розв’язання

Нехай і - дані мимобіжні прямі. Через довільну точку прямої проведемо пряму , паралельну , а через довільну точку прямої проведемо пряму , паралельну . Тепер проведемо дві площини – одну через прямі і , а другу через і . За теоремою про ознаку паралельності площин ці площини паралельні. У першій з них лежить пряма , а у другій – пряма .

4.               Доведіть, що через точку поза даною площиною можна провести площину, паралельну даній , і тільки одну.

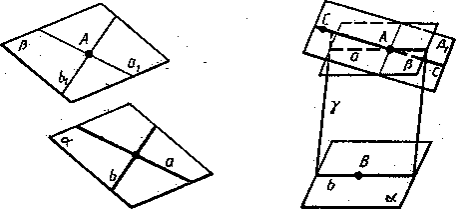
Розв’язання

Проведемо у даній площині які-небудь дві прямі і , що перетинаються. Через точку проведемо паралельні їм прямі і . Площина ,що проходить через і , за теоремою про ознаку паралельності площин паралельна площині .

Припустимо, що через точку проходить інша площина , теж паралельна площині . Позначимо на площині довільну точку , яка не лежить у площині . Проведемо площину через точки , і яку-небуть точку площини . Ця площина перетне площини , і по прямих , і . Прямі і не перетинають пряму , оскільки не перетинають площину . Отже, вони паралельні прямій . Але у площині через точку можна провести тільки одну пряму, паралельну прямій . Ми прийшли до суперечності. Теорему доведено.

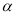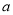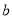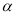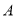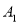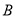5.               Через точку , яка лежить поза паралельними площинами і , проведено прямі і , що перетинають площину в точці і , а площину у точці і 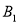відповідно. Знайдіть 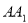, якщо: 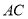=2см,  =6см, 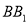=10см.

Розв’язання

і подібні ( - спільний, - як відповідні). , , (см).

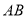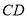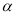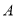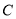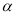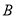6.               Паралельні відрізки і містяться між паралельними площинами і так, що точки і належать площині , а і 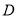- площині . Знайдіть 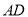і 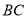, якщо 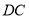=25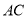см, =7см, 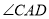=90⁰.

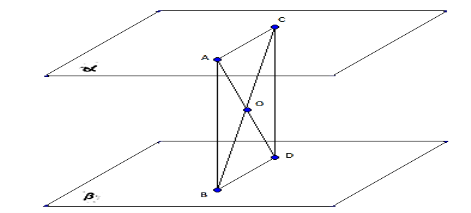
Розв’язання

За умовою сказано, що і з того, що і то , отже - паралелограм.

Розглянемо :

,

,

(см).

Розглянемо :

(см) – за властивістю діагоналей паралелограма;

,

,

(см).

6.                      Підбиття підсумків уроку.

Запитання до класу:

1.               Як можуть розміщуватися дві площини в просторі?
2.               Які площини називаються паралельними?
3.               Сформулюйте ознаку паралельності площин.

7.                      Домашнє завдання.

Вивчити теоретичний матеріал, з підручника «Бевз Г.П. Геометрія 10 кл.» №: 297(2,3,4), 299(2,3), 301, 305.