Урок "РОЗВ’ЯЗУВАННЯ ВПРАВ НА ЗАСТОСУВАННЯ ВЛАСТИВОСТЕЙ СТЕПЕНЯ З НАТУРАЛЬНИМ ПОКАЗНИКОМ"

Про матеріал

Урок з теми "РОЗВ’ЯЗУВАННЯ ВПРАВ НА ЗАСТОСУВАННЯ ВЛАСТИВОСТЕЙ СТЕПЕНЯ З НАТУРАЛЬНИМ ПОКАЗНИКОМ" допоможе навчити учнів застосовувати властивості степеня з натуральним показником при спрощенні виразів і розв’язуванні рівнянь, користуватися властивостями степеня при визначенні значень числових виразів та при порівнянні чисел

Перегляд файлу

УРОК № 7

ТЕМА УРОКУ: РОЗВ’ЯЗУВАННЯ ВПРАВ НА ЗАСТОСУВАННЯ ВЛАСТИВОСТЕЙ СТЕПЕНЯ З НАТУРАЛЬНИМ ПОКАЗНИКОМ

МЕТА УРОКУ:

НАВЧАЛЬНА: навчити застосовувати властивості степеня з натуральним показником при спрощенні виразів і розв’язуванні рівнянь, користуватися властивостями степеня при визначенні значень числових виразів та при порівнянні чисел

РОЗВИВАЮЧА: розвивати в учнів комунікативні компетентності, компетентності продуктивної творчої діяльності та саморозвитку і самоосвіти

ВИХОВНА: виховувати самостійність, лаконічність викладу думки, акуратність ведення записів, ретельність у виконавських діях тощо

Тип уроку: урок застосування знань, формування умінь та навичок учнів ХІД УРОКУ:

1.ОРГАНІЗАЦІЙНИЙ МОМЕНТ

Я хочу розпочати сьогоднішній урок із питання, яке, здається, недоречним на уроці математики: „Як ви гадаєте, чи знають дорослі люди та діти шкільного віку елементарні правила дорожнього руху?”

Ймовірна відповідь: „Так!”

А чи всі користуються ними, тобто чи всі застосовують правила дорожнього руху у реальних життєвих ситуаціях?

Ймовірна відповідь: „Ні!”

Нажаль, таких прикладів можна навести чимало. Ми знаємо правила, чули про закони, але користуватися ними не вміємо або користуємося невдало. В математиці, як у житті! Вивчив правило – чудово, а чи навчився їм користуватися? Ми з вами на минулому уроці познайомились і довели властивості степеня з натуральним показником, виходячи з цього, як ви гадаєте, чому ми маємо присвятити свій сьогоднішній урок?

Ймовірна відповідь: „Тому, щоб навчитися користуватися вивченими властивостями степеня на практиці.”

Дійсно, на сьогоднішньому уроці ми маємо навчитися застосовувати властивості степеня на практиці.

2.ПЕРЕВІРКА ДОМАШНЬОГО ЗАВДАННЯ

3.АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ

1.Технологія «Знайди помилку».

=
=
=
∙ =
∙ =
=
=
=
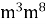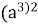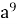
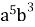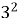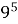
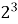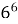
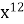
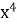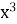
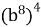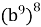
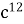
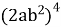= 2
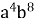
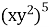= x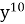
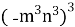= - 27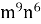

2. Фронтальне опитування учнів

1. Дайте визначення степеня з натуральним показником.

2. Як інакше називають другу та третю степінь числа?

3. Сформулюйте властивості степеня з натуральним показником.

4. Запишіть ці властивості у вигляді формул.

Властивості степеня з натуральним показником:

a^m ∙ aⁿ = a^m+n;

a^m : aⁿ = a^m-n; а ≠ 0, m > n

(a^m)ⁿ = a^m∙n;

(ab)ⁿ = aⁿbⁿ;

, b ≠ 0

5. Доведіть основну властивість.

4.ФОРМУВАННЯ ВМІНЬ УЧНІВ ДОВОДИТИ ТОЖНОСТІ

Колективне виконання завдань з підручника: № 217, 219, 221, 224, 225

5. ПІДБИТТЯ ПІДСУМКІВ УРОКУ

Давайте разом заповнимо пелюстки моєї „алгебраїчної ромашки”.

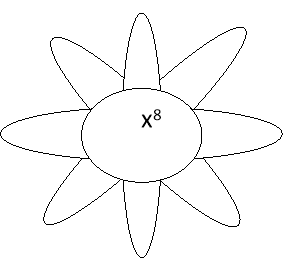Користуючись різними властивостями степеня, на пелюстках цих „ромашок” написати приклади, які б дорівнювали виразу в середині. Чим більше пелюсток, тим краще.