Урок "Відрізок. Довжина відрізка"

УРОК 11

Тема. Відрізок. Довжина відрізка

Мета: повторити й уточнити зміст понять «точка», «відрізок», «геометрична фігура»; сформувати вміння розпізнавати відрізки, зображувати їх за допомогою лінійки, описувати поняття «відрізок», «точка»; повторити співвідношення між основними одиницями вимірювання відрізків.

Тип уроку: повторення, систематизація та доповнення знань.

Хід уроку

І. Актуалізація опорних знань

Оскільки поняття відрізка і його довжини знайомі учням з початкової школи, під час вивчення цієї теми необхідно повторити й узагальнити набутий ними раніше досвід. Актуалізацію знань учнів провести під час виконання усних вправ.

Усні вправи

1.   Назвіть лінії і фігури, відомі з початкової школи (див. рис).    

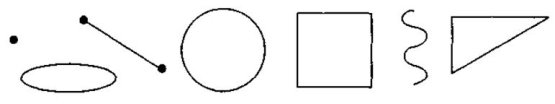
2.   Виразіть:

у міліметрах: а) 4 см; б) 6 см 3 мм; в) 5 дм;

у сантиметрах: а) 3 дм; б) 5 дм 4 см; в) 6 м; г) 900 мм;

у дециметрах: а) 5 м; б) 3 м 7 дм; в) 800 см; г) 1200 мм.

 II. Повторення і систематизація знань

Викладати матеріал уроку можна у вигляді практичної роботи. Послідовно виконуючи завдання, учні разом з учителем повторюють й систематизують навчальний матеріал.

1.   Позначте в зошиті дві точки А і В. Сполучіть їх між собою двома різними лініями.

Як сполучити точки А і В найкоротшою лінією? Як тепер називаються точки А і В?

Відповідь. Найкоротша лінія — відрізок АВ (ВА). А, В — кінці відрізка.

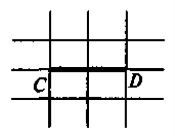
2.   Позначте в зошиті точки С і D на відстані 2 клітинок. Чому дорівнює довжина відрізка CD?

Відповідь. Довжина CD дорівнює 1 см або CD = 1 см.

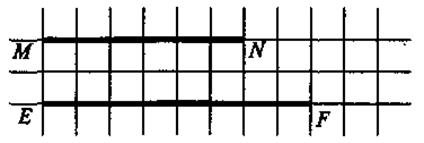
3.   Позначте в зошиті точки М і N на відстані 6 клітинок одна від одної; точки Е і F — на відстані 8 клітинок одна від одної. Чому дорівнюють довжини відрізків MN і СD?

Відповідь.  MN = 3 см; EF = 4 см.

4.   Подивіться на рисунок 9 (с. 17 підручника) і уявіть, що ми спробували накласти відрізок АВ на відрізок CD. Що при цьому ми помітимо? Як ви вважаєте, яку назву будуть мати ці (і такі самі за властивістю) відрізки?

5. Побудуйте два рівних відрізки у зошиті. Якими будуть їхні довжини? Відповідь. KP = OD = 2 см.

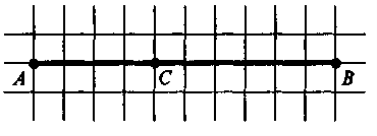
6.   Накресліть відрізок АВ довжиною 5 см. Поставте між точками А і В точку С. Де знаходиться точка С? Які нові фігури при цьому утворилися? Відмірте довжини частин і порівняйте їх суму з довжиною відрізка АВ. Що ви помітили?

Відповідь. С лежить між А і В (С належить відрізку АВ). АВ, АС, ВС — відрізки; АВ = 5 см; АС = 2см; ВС = 3 см; АВ = АС + ВС.

7. Робота з підручником (п. 3., с. 19).

Запитання до класу

1.   Скільки відрізків зображено на рис. 10?

2.   Чи можна провести відрізок так, щоб усі точки на рис. 10 лежали на цьому відрізку? (Ні, вважають, що такі точки не лежать на одній прямій.)

3.   Чи є на рис. 10 точка, що була б кінцем більш, ніж 2-х відрізків?

4.   Чи відрізняється кількість відрізків і розташування точок на рис. 11 від кількості відрізків і розташування точок на рис. 10? (Так само, як і на рис. 10, на рис. 11 маємо 4 відрізки, точки не лежать на одній прямій, але точка А є кінцем 3-х відрізків.)

Тому фігура на рис. 10 є ламаною, на рис. 11 — не є ламаною.

 ABCDE — ламана.

Точки А, В, C, D, E — вершини, відрізки АВ, ВС, CD, DE — ланки. Точки А і Е— кінці ламаної. Сума АВ + ВС + CD + DE — довжина ламаної.

8. Розглянемо мал 12. ст 18.

На малюнку зображено дві ламані ABCDEF і AВCD, кінці цих ламаних збігаються отже такі ламані називаються замкненими.

Висновки:

  найкоротша лінія, що сполучає дві різні точки — відрізок;

  дві точки, сполучені відрізком, називаються кінцями відрізка;

  відрізки можна вимірювати одиничними відрізками (1см; 1 дм; 1мм тощо);

  два відрізки, що сумістяться у разі накладання, називаються рівними; рівні відрізки мають однакові (рівні) довжини;

  точка ділить відрізок на два відрізки; якщо знайти довжину цих відрізків, то їх сума дорівнює довжині даного відрізка.

 відрізки утворюють ламану якщо кінець першого відрізка збігається з кінцем другого відрізка, кінець другого – з третім і так далі.

 довжина ламаної це сума довжин усіх її ланок.

  ламані кінці яких збігаються називаються замкненими.

 III. Відпрацювання навичок

 Якщо на попередньому етапі уроку учні показали досить високий рівень знань (виконання практичної роботи не викликало жодних ускладнень), то вже на цьому уроці можна розв'язувати з учнями не тільки завдання початкового і середнього рівнів, а й високого.

Усно можна виконати вправу № 45; після розгляду рисунка в) слід звернути увагу на залежність кількості відрізків, на які той ділиться точками, від кількості точок, що лежать на відрізку.

Письмові вправи

№ 48; 50 (Відпрацьовуємо навички побудови і вимірювання відрізків; в №50 — розглянути 2 способи знаходження довжини АС — вимірюванням та обчисленням; звернути увагу, що обчислення довжини — більш універсальний спосіб.)

 № 54, 57 , 60

 Додатково. Якщо залишиться час, розглянути № 62 (Ще раз звернути увагу учнів на те, що задачу треба розв'язати обчисленням, шукані довжини треба знайти, враховуючи, що АВ = АС – ВС, бо точка В лежить між A і C, і BD = BC+CD, бо С лежить між В і D.)

 IV. Підсумок уроку

Учитель пропонує дітям гру. До дошки виходять два учні, решта працюють у зошитах.

Слова учителя:

Всі на листочку

Поставимо точку (М).

Поряд з нею — другу,

Вірную подругу (N).

Хочу вас спитати:

Як же їх з'єднати?

Візьміть кольорові олівці і з'єднайте точки різними лінія­ми — прямими, кривими. Скільки кривих ліній можна провести? [Безліч.] Скільки прямих? [Одну.] Яка відстань від М до N найкоротша? (пряма)

Слід ще раз звернутися до рисунків і умовних записів, які було отримано під час практичної роботи (див. II), і повторити з учнями основні поняття уроку.

- Як позначають точки?

- Як позначають відрізок?

- Які ви знаєте одиниці довжини?

- Які відрізки називають рівними?

- Яку геометричну фігуру називають ламаною?

- Що називають довжиною ламаної?

- Яку ламану називають замкненою?

 V. Домашнє завдання

§1, п. 3, №№ 49; 51; 58; (63).