10 клас. Урок. "Механічна робота. Кінетична енергія. Потужність".

Урок 28

Тема. Механічна робота. Кінетична енергія. Потужність.

Мета. Формувати в учнів поняття енергії як кількісної міри руху, механічної роботи  та потужності як фізичних величин; пояснити зв'язок роботи й енергії на прикладі кінетичної енергії тіла; розвивати науковий світогляд, логічне мислення, увагу; виховувати інтерес до предмета.

Тип уроку. Урок вивчення нового матеріалу.

Хід уроку

І. Організаційний момент.

ІІ. Мотивація навчальної діяльності.

У повсякденному житті слово «робота» вживається дуже часто. Роботою називають будь-яку корисну працю робітника, вченого, учня. Як бачимо слово робота має велике значення: для позначення професії, для характеристики стану ( холодильник працює)..

У повсякденному житті  можна знайти багато різних тіл, при переміщенні яких може виконуватися робота. Так, випущена з рук кулька почне падати під дією сили тяжіння, яка виконуватиме роботу з переміщення кульки.

Стиснута пружина може підняти на певну висоту тягарець. Тут сила пружності виконає роботу з переміщення тягарця.

Поняття роботи у фізиці має певний сенс. І на сьогоднішньому уроці ми з вами про це поговоримо.

 

ІІІ. Вивчення нового матеріалу.

План

1. Що таке механічна робота?
2. Консервативні і неконсервативні сили.

А) Робота сили тяжіння.

Б) Робота сили пружності.

В) Робота сили тертя ковзання.

     3. Кінетична енергія.

4. Потужність?

Що таке механічна робота.

Ми дуже часто використовуємо поняття «робота» в повсякденному житті. Роботою називають і підйом цебра з колодязя, і доставку продуктів з магазина, і розв’язування складної задачі. Згадаємо, що загальноприйняте поняття «робота» відрізняється від поняття «механічна робота». Наприклад, у процесі підняття вантажу на висоту h поняття механічної та «біологічної» роботи збігаються.

Якщо ми просто тримаємо в руках певний вантаж і не пересуваємося, то ми виконуємо певну біологічну роботу при скороченні м’язів. З механічної точки зору, ніякої роботи тут не відбувається, тому що відсутнє переміщення.

Про механічну роботу говорять тоді, коли тіло змінює своє положення в просторі під дією сили.

З визначенням механічної роботи ми вже знайомі з курсу фізики 8 класу: якщо на тіло діє постійна сила , спрямована вздовж переміщення s тіла, то робота цієї сили .

Якщо сила спрямована під кутом а до переміщення тіла, то робота .

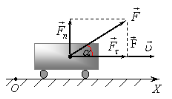Робота сили дорівнює добутку модуля сили на модуль переміщення й на косинус кута між напрямом сили й напрямом переміщення.

Одиницею вимірювання роботи в СІ є джоуль (Дж).

Один  джоуль — це робота, яку виконує сила в 1 Н в процесі переміщення

 тіла на 1 м у напрямі дії сили:  1 Дж = 1 Н · 1 м.

З формули для роботи випливає, що робота може бути позитивною, дорівнювати нулю й бути негативною, залежно від того, який кут становить напрям сили з напрямом переміщення:

А > 0,якщо  α< 90°;

А = 0, якщо  α = 90°;

А < 0, якщо α > 90°.

Консервативні сили

Сила, що діє на тіло, яке рухається поступально, називається консервативною (потенціальною), якщо робота, що виконується даною силою при переміщенні тіла, не залежить від того, по якій траєкторії відбулось це переміщення.

   При переміщенні тіла вздовж замкненої траєкторії робота консервативних сил рівна нулю (прикладом консервативних сил є сили гравітаційного притягання).

Неконсервативними силами є сили, які призводять до втрати механічної енергії, перетворюючи її в теплову. До таких сил належить сила тертя.

Робота сили тяжіння

Обчислимо роботу внутрішніх сил системи, що складається із Землі й піднятого над поверхнею Землі тіла.

Якщо тіло падає з певної висоти, напрям сили тяжіння збігається з напрямом переміщення. При цьому під час руху тіла вниз робота сили тяжіння позитивна. Якщо тіло масою m падає з висоти h, то робота сили тяжіння дорівнює: A = mgh

Під час руху тіла вгору сила тяжіння вже спрямована протилежно переміщенню, тому в цьому випадку робота сили тяжіння негативна. Отже, у разі підйому тіла масою m на висоту h робота сили тяжіння дорівнює:

 A = -mgh

Робота сили пружності

У разі зменшення деформації пружини сила пружності, що діє з боку пружини, спрямована так само, як переміщення, тому робота сили пружності позитивна.

Із закону Гука випливає, що в разі зменшення деформації пружини до нуля, модуль сили пружності зменшується від kx до нуля, тому середнє значе  ння сили пружності дорівнює: .

При цьому робота сили пружності визначається, як                                    .

 

У разі збільшення деформації пружини сила пружності, що діє на тіло з боку пружини, спрямована протилежно деформації. У цьому випадку робота сили пружності негативна.

Робота сили тертя ковзання

Сила тертя ковзання завжди спрямована протилежно напряму швидкості, а отже, і переміщенню тіла, тому робота сили тертя ковзання завжди негативна.

Кінетична енергія

Обчислимо роботу постійної сили , що діє на тіло масою m у випадку, коли тіло рухається прямолінійно, і напрям сили збігається з напрямом швидкості.

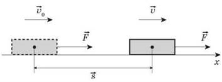Нехай тіло здійснило переміщення . У початковій точці спостереження тіло має швидкість ₀, а в кінцевій — . Спрямуємо вісь х так, щоб усі вектори мали з нею однаковий напрям.

Проекції всіх векторів дорівнюють модулям цих векторів. Робота сили дорівнює А = Fs, де F = mа. У разі прямолінійного рівноприскореного руху переміщення тіла та швидкість пов’язані співвідношенням:. Підставляючи у формулу роботи вираз для F і s, маємо:

, або

Величину, що дорівнює половині добутку маси тіла на квадрат його швидкості, називають кінетичною енергією тіла:  .

Будь-яке тіло, що рухається, має кінетичну енергію, пропорційну його масі та квадрату швидкості.

Енергія, яку має тіло внаслідок свого руху, називається кінетичною енергією.

Необхідно звернути увагу на те, що значення кінетичної енергії залежить від вибору системи відліку, адже кінетична енергія тіла залежить від його швидкості, а швидкість тіла в різних системах відліку різна. Якщо система відліку однозначно не зазначається, зазвичай мають на увазі систему відліку, пов’язану із Землею.

З урахуванням визначення кінетичної енергії можна записати: .

Отже, робота сили дорівнює зміні кінетичної енергії тіла.

Це твердження називають теоремою про кінетичну енергію. Якщо в початковий момент часу тіло нерухоме, то A = Е_k.

У цьому полягає фізичний зміст кінетичної енергії: кінетична енергія тіла масою m, що рухається зі швидкістю υ, дорівнює роботі, яку виконує сила, аби передати тілу, що перебуває в стані спокою, цю швидкість.

Кінетична енергія збільшується, якщо робота сили позитивна, і зменшується внаслідок негативної роботи.

Потужність

Для багатьох технічних завдань важливими є не лише виконувана робота, але й швидкість виконання роботи. Швидкість здійснення роботи характеризують фізичною величиною, яку називають потужністю.

Потужність — це фізична величина, що чисельно дорівнює відношенню роботи до проміжку часу, за який вона виконана.

P = F

 Одиниця потужності в СІ — ват (Вт):

1 Вт — це така потужність, яка дозволяє роботі в 1 Дж виконуватися за 1 с.

Це, порівняно, невелика одиниця. У техніці використовуються кіловат

(1 000 Вт), а іноді й мегават (10⁶ Вт).

Необхідна сила тяги обернено пропорційна швидкості автомобіля. Зі збільшенням швидкості водій може переходити на підвищені передачі. При цьому обертання коліс відбуватиметься з більшою швидкістю, але з меншим зусиллям.

Зазвичай швидкохідні автомобілі й потяги потребують двигунів великої потужності. Однак насправді в багатьох випадках сила опору не постійна, а зростає зі збільшенням швидкості. Якщо, наприклад, потрібно збільшити швидкість літака вдвічі, то потужність його двигунів потрібно збільшити у вісім разів. От чому так важко дається кожен новий успіх у збільшенні швидкості літаків, кораблів та інших транспортних засобів.

IV. Закріплення вивченого матеріал.

Бесіда.

1. У яких випадках робота позитивна? негативна? дорівнює нулю?
2. Морем пливе корабель. Чи виконує при цьому роботу сила тяжіння?
3. Чи виконує роботу сила тяжіння, що діє на супутник, який рухається навколо Землі коловою орбітою?
4. Позитивну чи негативну роботу виконує сила тяжіння, коли тіло ковзає вниз похилою площиною?
5. Як можна охарактеризувати швидкість виконання роботи?
6. Як за відомою потужністю обчислити роботу?
7. Від чого залежить швидкість рівномірного руху транспортного засобу, що приводиться в рух його двигуном?
8. Автомобіль рухається горизонтальною ділянкою дороги. Коли його двигун розвиває більшу потужність: під час повільної чи швидкої їзди?

Підсумок уроку

• Яку роботу — позитивну чи негативну — ми виконуємо, розтягуючи пружину? Яку роботу виконує при цьому сила пружності?
• Робота сили дорівнює добутку модуля сили на модуль переміщення й на косинус кута між напрямом сили й напрямом переміщення:
• A = FS cosα.
• Один джоуль — це робота, яку виконує сила в 1 Н у процесі переміщення тіла на 1 м у напрямі дії сили:
• 1 Дж = 1 Н · 1 м.
• Робота сили тяжіння: A = mgh.
• Робота сили пружності: .
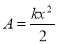• Робота сили тертя ковзання завжди негативна.

 

Домашнє завдання. Опрацювати §15 (Бар’яхтар )