Цикл уроків на тему "Додавання і віднімання натуральних чисел"

 

 

Історичні відомості про числа

Кількасот років тому з цифрами мало справу небагато лю­дей: вчені, збирачі податків, купці тощо. Нині ж цифри постійно нагадують нам про себе. Відрізки часу, температура повітря, но­мер будинку і квартири, номер школи тощо - все позначається цифрами. Цифри - це символи чисел, знаки, за допомогою яких чис­ла передають на письмі. Спочатку народилися числа, а вже по­тім - цифри. Спочатку люди навчилися лічити, "винайшли" чис­ло, а тоді знайшли спосіб записувати результати лічби.

Як же виникла лічба? З давніх-давен люди дошукувалися відповіді на це запитання. І в різних народів відповідь була не­однакова. Стародавні греки, наприклад, вважали, що людей на­вчив лічити Прометей. Той самий, що за легендою викрав у бо­гів вогонь і віддав його людям. Взагалі більшість народів появу числа пов'язувала з "діяннями" богів або ж міфічних героїв. Щоправда, інколи цю заслугу приписували людям, які насправді жили колись. Автори староруських рукописів, наприклад, вва­жали, що лічбу винайшов Піфагор - старогрецький математик, який жив у VI столітті до нашої ери. Піфагор був великим мате­матиком, але ж люди вміли лічити задовго до VI століття! І не просто вміли лічити, а й мали вчених, які писали математичні книги. Найдавніша математична книга дійшла до нас з другого тисячоліття до нашої ери.

        Доведено, що був час, коли люди обходилися без чисел. Наприклад, мешканці австралійських джунглів, бажаючи обмі­нятися продуктами, чинили так. Люди одного племені клали на землю в'язки їстівного коріння, а другого - навпроти кожної та­кої в'язки ставили кошик з рибою. Встановивши відповідність цих множин (між в'язками й кошиками), провадили обмін.

        З розвитком людства лічба ставала потребою, а пальці рук і ніг довго були знаряддям лічби. Як люди використовували па­льці для лічби, покажемо на прикладі індіанців племені таманака (Південна Америка). Замість "один" індіанці говорять "палець" і обов'язково показують палець. Назви деяких інших чисел цього племені подано в таблиці:

Числа	Назви чисел у індіанців
Два	Два пальці
Чотири	Чотири пальці
П'ять	Рука
Шість	Палець на другій руці
Десять	Дві руки
Одинадцять	Палець на одній нозі
П'ятнадцять	Нога і дві руки
Шістнадцять	Палець на другій нозі
Двадцять	Людина
Двадцять один	Один палець на руці другої людини
Сто	П'ять людей

          Ще й зараз деякі відсталі народи та малі діти користуються пальцями  при лічбі.

           Є підстави гадати, що єгиптяни лічили за допомогою лічильної  дошки із накресленими на ній смугами. На кожній смузі розкладали камінці - їх було не більше дев'яти. Щоразу, коли доводилося класти десятий камінець, з цієї смуги скидали всі камінці на сусідню, праву, смугу клали один камінець. Таким чином, єгиптяни лічили, як ми. Можна гадати, що їхня лічильна дошка була прообразом нашої рахівниці.

           Уміння лічити і записувати результати лічби прийшло до людей  з життєвим досвідом. Саме життя спонукало людину до цього.

         Спочатку кількість передавали за допомогою малюнка. Приміром, щоб показати число 1, малювали 1 палець, 2 - два пальці, 10 - з'єднані руки, 100 - згорнуту вимірну мотузку, 1000 - квітку лотоса. Взагалі квітка лотоса була символом великого числа. Цей спосіб запису чисел застосовували в стародавніх кра­їнах - Єгипті і Китаї. Греки ще в V столітті до нашої ери назвали такі знаки ієрогліфами - "священним різьбленням".

         З розвитком писемності, зокрема буквеного письма, числа почали записувати словами. Спочатку записували повністю, по­тім скорочено, використовуючи лише першу літеру числівника. Стародавні математики прийшли до висновку: це не дуже зручно, і от у V столітті до нашої ери зароджується нова алфавітна система нумерації: першими дев'ятьма літерами позначали оди­ниці (від 1 до 9), наступні дев'ять літер використовувалися для позначення десятків (від 10 до 90), а ті, що йшли за ними, дев'ять літер - для позначення сотень (від 100 до 900).

         Проте у щойно згаданих систем нумерації - ієрогліфічній та алфавітній - був один досить суттєвий недолік: ієрогліфічні знаки й літери не мали чітко визначеного місця - позиції. Такий запис дуже ускладнював обчислення. Щоправда, ще у стародав­ньому Вавілоні, де користувалися своєрідним письмом - клино­писом і де числа позначали тими ж значками-клинцями, вже на­магалися закріпити за одиницями, десятками, сотнями певне мі­сце. До цього вавілонян змушувала обмежена можливість їхньо­го письма. Клинці є клинці, багато їх не вигадаєш! От і додума­лися закріпити за певними розрядами чисел певне місце. Значно пізніше, з другого століття нової ери, цю спробу самостійно по­чали розвивати в Греції, а незабаром позиційний запис чисел удосконалюють в Індії. Саме індійська система лягла в основу нашої нинішньої системи числення.

        Систему числення, основану на позначенні всіх натураль­них чисел десятьма знаками - цифрами, вперше описав і засто­сував у IX столітті талановитий син узбецького народу Магомет син Муси із Хорезму в рукописі "Арифметика індорум".

         У Європі нова система нумерації стала відома на початку XIII століття завдяки італійському вченому Леонардо Пізанському, який описав її в 1202 році у своїй праці "Книга обчис­лень". Але утвердилася ця система в Західній Європі значно піз­ніше - у ХУ-ХУІ століттях.

         На Русі про арабсько-індійську систему знали ще в XIII столітті. Так на одному знайденому дзвоні, виготовленому у ті часи, знаходимо цю нову нумерацію. На початку XVII століття цими цифрами вже нумерують сторінки російських книг, їх кар­бують на золотих монетах. А в середині століття ними користу­ються в рукописних працях. В 1703 році в "Арифметиці" Леонтія Магницького усе арифметичне вчення викладене на основі по­зиційної системи числення, і тільки сторінки підручника позна­чені слов'янською нумерацією.

       Як виникло саме слово цифра? Походить воно від арабського слова "сифр", що в перекладі означає "порожнє місце". Річ . і їм, що індійці не мали чим позначати відсутність розрядного Числа і там, де нині стоїть нуль, ставили крапку, яку називали "сифр". Коли ж з'явився нуль, його також стали називати циф­рою. Так було до XVIII століття - поки він дістав своє наймення під латинського слова "нулюс", що означає "ніякий". А цифрами пали називати символи чисел взагалі.

      Назви десяти цифр у всіх слов'ян дуже схожі, їх можна пі-шати, коли говорять чех, поляк, болгарин, серб, українець, росі­янин, білорус. А от назви великих чисел різняться помітно, бо Г являлися пізніше. І кожен народ виробляв свої найменування. Ми кажемо, наприклад, двадцять п'ять, а чехи - п'ять і два­дцять; ми кажемо сорок, а поляки - чтердзесці (чотири десят­ки).З операціями додавання і віднімання люди мали справу за­довго до того, як числа дістали імена. Коли кілька груп збирачів ягід або рибалок складали в одне місце свою здобич, вони вико­нували операцію додавання. Правда, при цьому додавались не числа, а сукупності (або, як говорять математики, множини) предметів, але операція додавання чисел якраз описує додавання сукупностей предметів. А коли із зібраних горіхів частина вико­ристовувалася в їжу, люди виконували віднімання - запас горі­хів зменшувався.

        З операцією множення люди познайомилися, коли почали сіяти хліб і побачили, що зібраний врожай у кілька разів біль­ший, ніж кількість посіяного зерна. Говорили: зібраний врожай "сам - двадцять" (у двадцять разів більше зібрали, ніж посіяли), "сам - сорок" і т.д. Нарешті, коли здобуте на полюванні м'ясо тварин або зібрані горіхи ділили порівну між усіма членами племені, виконували операцію ділення.

        Самі назви цих операцій показують, з якими діями над предметами вони пов'язані. Але повинні були пройти тисячоліт­тя, поки люди зрозуміли, що додавати, віднімати, множити і ді­лити можна не самі сукупності предметів, а числа.

         Знаки арифметичних дій, рівності та нерівності з'явилися у такому вигляді, як ми їх знаємо, з поширенням у Європі арабсь­кого написання чисел. Звичайно, не всі зразу.

         Першими народилися знаки додавання "+" і віднімання їх наприкінці XV століття застосував лейпцігський профе­сор Ян Відман у творі "Швидка і красива лічба для всього купе­цтва".

         Але ж люди вміли віднімати й додавати і раніше! Як же позначали ці дії на письмі? У різних народів по-різному. Єгип­тяни, наприклад, коли хотіли додати два числа, схематично ма­лювали дві людські ноги, що "рухалися" вперед, а при відніман­ні ступні цих ніг скеровували в зворотному напрямку. У старо­давніх греків додавання позначали вертикальною рискою, а від­німання - значком, схожим на кому. У Європі дію додавання ще позначали літерою "р" або "Р" (початкова літера латинського слова "плюс" - більше), а віднімання "т" або "М" (від латинсь­кого "мінус" - менше). Однак ці позначення не прижилися.

           Знак множення "х" - навскісний хрест - знаходимо у праці англійського математика Уїльяма Оутреда "Математичний ключ" (1631 рік). Згодом, у 1698 році, видатний німецький математик Готфрід-Вільгельм Лейбніц дію множення запропонував переда­вати крапкою (•), а трохи раніше, у 1684 році, впровадив дві крап­ки (:) для позначення ділення. Щоправда, ці знаки дістали загаль­не визнання і набули поширення лише у XVIII столітті завдяки підручникам німецького математика Хрістіана Вольфа.

           Знак рівності "=" ввів англійський учений Роберт Рекорд ще в XVI столітті. На його думку, ніщо не може передати рівність так, як два однакових паралельних відрізки. До нього в математи­ці користувалися іншими знаками рівності. Так старогрецький математик Діофант відношення рівності позначав літерою "і" (по­чаткова у слові "ізос" - рівний). Індійські й арабські математики, а також більшість європейських, найчастіше, аж до XVII століття, вживали для цього повністю або скорочено слово "рівний".

           Знаки "<" і ">" для позначення відношень нерівності сис­тематично . почав застосовувати англійський математик Томас Гарріот. Його книжка, де він вживає ці знаки, побачила світ у 1631 році.

           Дужки круглі знаходимо у математичних творах першої половини                 XV століття. До їхньої появи ставили риски над вира­зом, якого вони стосувалися, або ж під ним, що було дуже не­зручно під час друкування.

          Знак ділення й дробу - горизонтальна риска - вперше зустрічається у згадуваного вже нами італійського математика Ле­онардо Пізанського, який, мабуть, запозичив його з арабських  рукописів. Для зручності в друкуванні англієць Август де Морган замінив  горизонтальну риску навскісною.

         Наука, яка почала вивчати числа і дії над ними, дістала на­шу "арифметика" (від грецького arithmos, що означає "число"). 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

                                                               Урок № 1.

Тема. Додавання натуральних чисел.

Мета: повторити і систематизувати знання учнів про правила дода­вання натуральних чисел; відпрацювати навички додавання багатоцифрових натуральних чисел і використання додавання натуральних чисел до розв'язання задач.

Тип уроку: узагальнення і систематизація знань учнів.

 

Хід уроку

I. Актуалізація опорних знань

Усні вправи

1. Число 105 збільшити на 45.
2. Яке число більше за 90 на 80?
3. Число 59 на 11 менше другого числа. Чому дорівнює друге число?

 

II. Повторення і систематизація знань учнів

Запитання до класу

1. Відомо, що число а збільшили на число b. Отримали число с. Якою дією можна знайти результат с?
2. Відомо, що число с на b більше від числа а. Як знайти число с, якщо а і b відомі?
3. Число а на b одиниць менше від числа с. Як знайти с, якщо а і b відомі?
   [Зрозуміло, що на всі запитання відповідь одна: а + b = с]
4. Отже, в яких випадках виконується додавання чисел а і b?
5. Нехай а + b = с. Як називаються числа а і b при цьому? Як називається число с?
6. Чи може сума двох чисел дорівнювати одному з доданків?

Після отримання відповідей на запитання вчитель на дошці, а учні в зошитах роблять запис:

а + b = с а, b  —  доданки, а + b, с — сума.

а + 0 = а

0 + 0 = 0

Далі вчитель нагадує правило додавання багатоцифрових чисел та його застосування для додавання величин (у зошитах учні запишуть при­клади 1 і 2, які вчитель розбирає біля дошки).

Приклад 1
Приклад 2		або

 

III. Відпрацювання навичок

Усні вправи

1. Знайдіть значення суми чисел: 1) 14 і 16; 2) 70 і 85; 3) 92 і 3000.
2. Наталка і Миколка розв'язували задачі. Миколка розв'язав 26 задач, а Наталка на 6 задач більше. Скільки задач розв'язала Наталка? Скільки задач розв'язали Наталка і Миколка разом?
3. Виразіть: 1) у сантиметрах — 76 м 34 см; 2) у метрах — 16 км 527 м; 3) у секундах — 5 хв 15 с; 4) у місяцях — 3 роки 5 міс.
4. № 1, с.60.

Письмові вправи

 На цьому уроці бажано запропонувати різноманітні завдання на дода­вання натуральних чисел як обов'язкового рівня:

 

Додатково

Логічні вправи. Встановити пропущені числа, слова чи малюнки.

 

а) А С Т Р О Ї Д А VIII математик ? [IX]

б) Розгадайте анаграму і знайдіть зайве слово: мюйд, туф, тіколь, адоб [дюйм, фут, лікоть; доба — зайве слово]

 

IV. Домашнє завдання (відповідно до підручника)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

                                                             Урок № 2.

Тема. Додавання натуральних чисел. Властивості додавання.

Мета: повторити і систематизувати знання учнів про правила дода­вання натуральних чисел; відпрацювати навички додавання багатоцифрових натуральних чисел і використання додавання натуральних чисел до розв'язання задач.

Тип уроку: узагальнення і систематизація знань учнів.

 

Хід уроку

I. Перевірка домашнього завдання

 

II. Актуалізація опорних знань

Усні вправи

1. Знайдіть суму доданків: 24 і 36; 18 і 22; 13 і 47; 51 і 49.
2. Плитка шоколаду коштує 2 грн. 40 к., а тістечко — 70 к Скільки коштують: 1) плитка шоколаду і тістечко; 2) плитка шоколаду і два тістечка; 3) дві плитки шоколаду і тістечко?
3. Сума двох чисел більша за одне з них на 237. Чому дорівнює друге число?

 

«Мозкова атака»

Ця гра допомагає пошуку оптимального розв’язку поставленої проблеми. Виходять по одному учню з кожної команди. Учитель ставить запитання. Учні повертаються в свої команди, вислуховують думки кожного члена команди, вибирають натуральний розв’язок, повертаються за ігровий стіл і відповідають.

 

   Запитання

1. Якщо о 12 годині ночі йде дощ, чи можна сподіватись, що через 72 години буде сонячна погода?

(Відповідь: не можна, оскільки через 72 години  (через 3 доби) буде знову 12 годин ночі, а сонце вночі не світить).

2. Дайте відповідь на запитання: скільки в кімнаті кішок, якщо в кожному з чотирьох кутів кімнати сидить по одній кішці, а напроти кожної кішки сидить по три кішки і на хвості у кожної кішки сидить по кішці?

(Відповідь: 4 кішки).

3. Копав Івась картоплю,

Та швидко він копав:

За кожні півгодини сім відер набирав.

Попрацював він п’ять годин,

Пішов відпочивати.

Так скільки встиг картоплі

Іванко накопати?

   (Відповідь: 70 відер).

4. – Ти, Вітю,- каже Леся, -

Досвідчений юннат.

Не міг би ти штук 10 метеликів спіймати?...

Узяв сачок на плечі

Й пішов юннат у ліс.

Прийшов він аж надвечір…

• То скільки ж ти приніс? –

Питають у юнната .

А Вітя каже: «Ох,

Лишилось сім піймати, якщо спіймаю трьох…»

То може з вас хто, діти, уже підрахував:

Скільки ж в лісі Вітя

Метеликів спіймав?

   (Відповідь: жодного).

 

IV. Формування навичок
Усні вправи

1. Знайти суму найбільш зручним способом.

1) 26 + 19 + 34 + 51; 2) 32 + 29 + 28 + 41; 3) 630 + 40 + 160 + 70:

2. Збільшити суму чисел 37 і 18 на 13.

Письмові вправи

1. Який із зазначених порядків виконання дій є найзручнішим для об­числення суми

83 + 127 + 273 + 417?

 1) (273 + 417) + (127 + 83); 2) (273 + 127) + (417 + 83);

 3) (417 + 127) + (273 + 83); 4) (83 + 127) + (417 + 273).

2) У якій з наведених сум вирази в дужках рівні?

 1) (0 + 132) + (132 + 1);  2) (731 + 13) + (702 + 42);

 3) (67 + 22) + (43 + 45);  4) (30 + 40) + (75 + 0).

3) Яке число треба поставити замість *, щоб сума 224 + * + 1276 дорівнювала 2500?

 1) 100; 2) 0; 3) 50; 4) 1000.

4) Яке з наведених чисел дорівнює сумі 4 м 76 см + 3 м 48 см?
1) 7 м 76 см; 2) 7 м 48 см; 3) 8 м 24 см; 4) 7 м 124 см.

 

V. Домашнє завдання (відповідно до підручника)

 

 

 

 

 

 

 

 

 

Урок № 3.

Тема. Додавання натуральних чисел. Властивості додавання.

Мета: повторити і систематизувати знання учнів про правила дода­вання натуральних чисел; відпрацювати навички додавання багатоцифрових натуральних чисел і використання додавання натуральних чисел до розв'язання задач.

Тип уроку: узагальнення і систематизація знань учнів.

 

Хід уроку

I. Перевірка домашнього завдання

 

II. Актуалізація опорних знань

Усні вправи

1. Ігровий момент

 Учитель нагадує учням, що найкраще додавання виконується, коли хоча б один з двох доданків — кругле число (закінчується на 0).

Зараз ми проведемо гру: ведучий (спочатку вчитель, а потім будь-хто з учнів) називає одноцифрове (двоцифрове) число, а будь-хто з гравців (учні класу) називають таке, щоб сума двох названих чисел була круглим числом.

(Наприклад, ведучий називає число 27, гравець — 13.)

Можна модифікувати гру так, щоб залучити до неї якомога більше учнів (наприклад, учні розбиваються на 2 команди, одна називає перший, інша — другий доданок, а ведучий перевіряє правильність).

Після виконання № 1 доречними будуть такі завдання:

2. Виконайте додавання, вибравши найбільш зручний порядок вико­нання дій.

1) (3 + 71) + 19;   2) 16 + (89 + 184);

3) 13 + 18 + 17 + 22;  4) 38 + 47 + 53 + 62.

3. Спростіть вираз:

1) (14 + п) + 16; 2) 17 + (п + 43);  3) 71 + b + 29;  4) с + 293 + 207.
Які властивості було вами використано в №№ 2, З?

 

Запитання – жарти

 Учням кожної команди дається 5 слів. Із них 4 об’єднані загальною ознакою. Знайти зайве п’яте слово.

1. Додавання, множення, ділення, доданок, віднімання.
2. Секунда, година, рік, вечір, тиждень.

 

III. Відпрацювання навичок

 Оскільки в більшості учнів вміння виконувати додавання багатоциф-рових чисел сформовані, бажано на цьому уроці організувати роботу так, щоб якомога більше часу учні працювали самостійно.

Письмово:

№ 1. Спростіть вираз:

 1) (14 + п) + 16;

 2) 17 + (п + 43); 

 3) 71 + b + 29; 

 4) с + 293 + 207.

 

№ 2. Розв´яжіть рівняння:

 1) х + 132 785 = 455 712;

 2) 17 397 – х = 3 612; 

 3) 71 449 – b = 29 307; 

 4) с + 293 207 = 407 891.

№ 3. Обчисліть:

 1) 76 м 39 см – 41 м 24 см;

 2) 7 год 5 хв – 5 год 34 хв;

 3) 2 год 12 хв – 40 хв;

 4) 7 км – 6 987 м;

 5) 3 ц + 302 кг.

 

V. Домашнє завдання (відповідно до підручника)

 

VІ. Підсумок уроку: 

Продовжіть речення.

• Я сьогодні дізнався…
• Я сьогодні запам´ятав…
• Я сьогодні зрозумів…
• Мені варто звернути увагу на завдання….
• Я хочу більше дізнатися про…

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Урок № 4.

Тема. Додавання натуральних чисел. Властивості додавання.

Мета: закріпити знання учнів про властивості додавання натуральних чисел; відпрацювати навички додавання багатоцифрових натуральних чисел; додавання величин і застосування переставної та сполучної вла­стивостей додавання для раціоналізації обчислень.

Тип уроку: застосування знань, навичок та вмінь.

Обладнання: таблиця-схема «Властивості додавання».

Хід уроку

І. Перевірка домашнього завдання

На дошці скорочено записане розв'язання домашніх вправ.

 

 

II. Актуалізація опорних знань

Під час повторення матеріалу зручно буде спиратися на таблицю-схему (див. табл.).

Властивості додавання

1. Переставна а + b = b+ a.	Приклад:  64 + 23 = 23 + 64
2. Сполучна (a + b) + c = b + (a + c) = a + (b + c)	Приклад: 1) (64 + 23) + 77 = 64 + (23 + 77) =      = 64 + 100 = 164. 2) 136 + (а + 214) =136 + (214 + а) =      = (136 + 214) + а = 350 + а. 3) 37 + 29 + 13 + 41 =      = (37 + 13) + (29 + 41) = -50 + 70 = 120

Усні вправи

1. Виконайте додавання, вибравши найбільш зручний порядок вико­нання дій.

1) (3 + 71) + 19;   2) 16 + (89 + 184);

3) 13 + 18 + 17 + 22;  4) 38 + 47 + 53 + 62.

2. Спростіть вираз:

1) (14 + п) + 16; 2) 17 + (п + 43);  3) 71 + b + 29;  4) с + 293 + 207.
Які властивості було вами використано в №№ 2, З?

 

III. Відпрацювання навичок

 Оскільки в більшості учнів вміння виконувати додавання багатоциф-рових чисел сформовані, бажано на цьому уроці організувати роботу так, щоб якомога більше часу учні працювали самостійно.

Розв'язання задач

№№ 179 (2, 4, 6); 183 (2, 4, 6, 8); 189 (2, 4, 6, 8); 194 (2, 4, 6, 8); 186.

 

IV. Перевірка засвоєння матеріалу та рівня сформованості вмінь і навичок учнів

Тестова самостійна робота

Варіант 1

1. Який із зазначених порядків виконання дій є найзручнішим для об­числення суми 83 + 127 + 273 + 417?

1) (273 + 417) + (127 + 83); 2) (273 + 127) + (417 + 83);

3) (417 + 127) + (273 + 83); 4) (83 + 127) + (417 + 273).

2. У якій з наведених сум вирази в дужках рівні?

1) (0 + 132) + (132 + 1);  2) (731 + 13) + (702 + 42);

3) (67 + 22) + (43 + 45);  4) (30 + 40) + (75 + 0).

3. Яке число треба поставити замість *, щоб сума 224 + * + 1276 дорівнюва­ла 2500?

1) 100; 2) 0; 3) 50; 4) 1000.

4. Яке з наведених чисел дорівнює сумі 4 м 76 см + 3 м 48 см?
   1) 7 м 76 см; 2) 7 м 48 см; 3) 8 м 24 см; 4) 7 м 124 см.

 

Варіант 2

1. Який із зазначених порядків виконання дій є найзручнішим для об­числення суми 158 + 388 + 1012 + 1242?

1) (158 + 388) + (1012 + 1242); 2) (1242 + 1012) + (388 + 158);

3) (1012 + 388) + (158 + 1242); 4) (1242 + 388) + (1012 + 158).

2. У якій з наведених сум вирази в дужках рівні?

1) (203 + 0) + (1 + 203);  2) (135 + 25) + (0 + 160);

3) (290 + 5) + (209 + 95); 4) (707 + 7) + (770 + 70).

3. Яке число треба поставити замість *, щоб сума 240 + * + 637 дорівнюва­ла 1637?

1) 1000; 2) 870; 3) 0; 4) 760.

4. Яка з величин є значенням суми 3 год 28 хв + 5 год 35 хв?
   1) 8 год 63 хв; 2) 9 год 3 хв; 3) 8 год 28 хв; 4) 8 год 3 хв.

 

V. Домашнє завдання (відповідно до підручника)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

                                                             Урок № 5.

Тема. Віднімання натуральних чисел.

Мета: ввести поняття і зміст дії віднімання; сформувати навички віднімання багатоцифрових чисел.

Тип уроку: засвоєння нових знань.

 

Хід уроку

І. Перевірка домашнього завдання.

 

ІІ. Аналіз самостійної роботи

ІІІ. Актуалізація опорних знань

Усні вправи

1. Суму чисел 19 і 8 зменшити на 27.
2. Від числа 53 відніміть суму чисел 13 і 17.
3. Які з наведених записів є записами одного й того ж самого числа?

1) 300 + 40 + 5; 2) 3000 + 400 + 5;  3) 3405;

4) 3 · 1000 + 4 · 100 + 5 · 1;  5) 3045; 6) 345.

ІV. Засвоєння знань

Щоб  водить  кораблі, щоб  у  небо  злітати,

Треба  перш за усе математику  знати.

І  щоб  лікарем  стати, і у  космос  літати –

Треба  перш  за  усе математику  знати.

Хто  науку  цю  цікаву добре  знатиме,

Той  ніколи  в  кожнім  ділі не  блукатиме.

Задача 1. Група туристів, що складається з 14 осіб, пішла в похід місцями бойової слави. П'ять туристів поїхали автобусом, а решта відпра­вились пішки. Скільки туристів відправилось пішки?

 Аналіз розв'язання

Якщо число туристів, які подорожували пішки, невідоме (позначимо його літерою х), то умову задачі можна записати так: 5 + х = 14.

Тобто в задачі треба за відомою сумою двох чисел (14) і одним відомим доданком (5) знайти невідомий доданок (х), який знаходимо відніман­ням:

х = 14 – 5; х = 9.

Отже, відняти від числа 14 число 5 — означає, що треба знайти таке число х, яке в сумі з числом 5 дає число 14.

Задача 2. На кінець І семестру у 5 класі було 18 учнів, що вчаться на достатньому рівні. Але за II семестр кількість таких учнів збільшилась, і на кінець року таких стало 23 учні. На скільки збільшилась кількість учнів 5 класу, що навчаються на достатньому рівні?

Розв'язання

Якщо шукана кількість учнів невідома (позначимо її літерою х), то умову задачі можна записати так: 18 + х = 23. Отже, знову в задачі знаходи­мо невідомий доданок (х) за відомою сумою (23) і другим відомим додан­ком (18). Зрозуміло, що х = 23 – 18; х = 5 і відняти від 23 число 18 — означає, що треба знайти таке х, яке б у сумі з числом 18 дало число 23.

Після цих пояснень навіть учні можуть сформулювати означення:

Відняти від числа а число b — означає знайти таке число х, яке б у сумі з b давало число а:

a – b = x, х + b = а.

При цьому а — зменшуване; b — від'ємник; а – b, х — різниця.

Зауваження. З означення віднімання випливає, що правильність від­німання перевіряється додаванням (до різниці додати від'ємник, щоб от­римати зменшуване).

Приклад

Що означає відняти: 1) від 18 число 9; 2) число 7 від 12?

Як перевірити правильність виконання дії віднімання?

Задача 3

1) На скільки число 62 більше від 38?

2) На скільки 49 менше за 81?

    Щоб відповісти на запитання, треба відняти:

1) 62 – 38 = 24; 2) 81 – 49 = 32

Отже, різниця а і b показує, на скільки а більше від b, або на скільки b менше від а.

Задача 4. На яке число треба зменшити число 24; 38; 1; 0, щоб отримати

1) нуль; 2) ці самі числа

Розв'язання. З властивостей додавання відомо, що а + 0= а, отже, за оз­наченням віднімання, 0 = а – а, а = а – 0, тобто:

1) 24 – 24 = 0; 38 – 38 = 0; 1 – 1 = 0; 0 – 0 = 0;

2) 24 – 0 = 24; 38 – 0 = 38; 1 – 0 = 1; 0 – 0 = 0.

Завдання 5. Як додати 23 795 до 7 459? Як знайти різницю цих чисел?

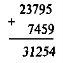
Отже, віднімання виконується теж «у стовпчик». Правильність вико­нання можна перевіряти додаванням:

  

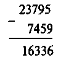
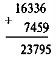
V. Закріплення знань

1. Що нового вивчили на уроці?
2. Як підписати багатоцифрові числа при письмовому відніманні?
3. Що означає від одного числа відняти інше?
4. Чи може бути різниця більшою за зменшуване?
5. Коли різниця дорівнює зменшуваному?

 

VІ. Домашнє завдання (відповідно до підручника)

 

 

 

 

 

 

Урок № 6.

Тема. Віднімання натуральних чисел.

Мета: пояснити учням, що віднімання, як і додавання натуральних чисел, можна виконувати, використовуючи певні властивості; сформува­ти вміння учнів використовувати властивості віднімання під час виконан­ня обчислень; продовжувати відпрацьовувати навички віднімання бага­тоцифрових чисел.

Тип уроку: засвоєння навичок та вмінь.

 

Хід уроку

І. Перевірка домашнього завдання.

ІІ. Актуалізація опорних знань

Усні вправи

1. Яке число треба додати до 17, щоб отримати 53?
2. Від якого числа треба відняти 47, щоб отримати 17?
3. Яке число треба відняти від 72, щоб отримати 34?
4. Поставте замість квадратиків такі числа, щоб рівності стали правиль­ними:

219 + □ = 219;  317 – □ = 317; 711 – □ = 0;  219 + 314 + □ = 1314;

89 + □ + 74 + □ = 200; 387 + □ + □ + 13 = 1000.

Відгадати загадки:

1. Чисел  натуральних у світі є багато.

Серед них найбільше не зможемо назвати.

А найменше знать годиться

Це звичайно…

       (Одиниця)

2. У навчанні нам допомагає,

Про числа він розповідає,

Відрізки, формули, кути –

Його нам треба берегти.

Повинен знати кожен учень,

Що це наш друг і помічник…

       (Підручник)

3. Десять їх. Це не багато.

Як усі їх будеш знати,

Зможеш будь-яке число

Легко записати.

Пишуться красиво й стисло.

Що це, діти? Та це ж…

       (Цифри)

IIІ. Формування знань

Завдання 1. Обчисліть:

1) 428 – (128 + 126); 2) (428 – 128) – 126; 3) (428 – 126) – 128;

4) (619 + 282) – 219;  5) (619 – 219) + 282;  6) (282 – 219) + 619.

Порівняйте відповіді у прикладах 1) і 2), 3); 4), 5) і 6). Що ви помітили?

Завдання 2. Знайдіть серед виразів рівні:

1) 65 – (а + 45); 2) (65 – а) + 45; 3) (65 – а) – 45; 4) (65 – 45) – а;

5) (65 + а) – 45; 6) (65 – 45) + а; 7) (65 – 45) – а; 8) (а – 45) + 65.

Отже, іноді для обчислень зручніше використовувати властивості віднімання, що можна записати за допомогою літер (замінивши їх числа­ми) так:

(Відкривається таблиця-схема «Віднімання натуральних чисел. Вла­стивості віднімання».)

Схема-таблиця «Віднімання натуральних чисел. Властивості віднімання»

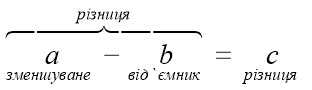
a = b + c

 

Властивості:

1. а - а = 0;   2. а – 0 = а;

3. 0 – 0 = 0;   4. а – (b + с) = (а – b) – с = (а – с) – b;

5. (а + b) – с = (а – с) + b = (b – с) + а.

 

IV. Закріплення знань учнів

Вправи для письмового виконання

1. Обчисліть: 28 – (18 + 3);   45 – (35 + 7); (88 + 17) – 28;   (79 + 14) – 14.
2. Спростіть вираз: 28 – (18 + а);   45 – (35 + b);   (88 + х) – 28; (y + 14) – 14.

 

Додатково

1. Порівняйте значення виразів:

1) (36 + 30) : 11 і (34 – 22) : 2; 2) 79 – 34 + 156 : 2 : 6 і (216 + 197) : 7.

2. Перевірте, чи правильна нерівність:

1896 – (635 + 458) < 2400 – (1729 – 123).

3. У залі для глядачів т рядів, а в кожному ряду на 5 місць більше, ніж кількість рядів. Скільки місць в залі для глядачів? Складіть вираз для розв'язання задачі, знайдіть його значення, якщо т = 15; 20.
4. Знайдіть значення виразу, обираючи зручний порядок обчислень:

1) (524 + 397) – 224; 2) 877 – (377 + 216); 3) (325 + 419) + 675;

4) 631 + 308 + 1369 + 692.

5. Спростіть вираз:

1) (63 + х) + 29; 2) а + 614 + 235; 3) (22 + а) – 7; 4) 69 – (т + 12).

6. На першій зупинці з автобуса вийшло 11 пасажирів, а ввійшло 6. На другій зупинці вийшло 8, а ввійшло 15. Скільки пасажирів було в автобусі до першої зупинки, якщо після другої зупинки їх стало 30?

 

V. Домашнє завдання (відповідно до підручника)

                                                             Урок № 7.

Тема уроку: Розв’язування   вправ   на   додавання   та  віднімання  натуральних чисел

Мета:            

освітня: вдосконалювати вміння учнів виконувати додавання і віднімання натуральних чисел,  використовувати властивості додавання і віднімання натуральних чисел під час розв’язування вправ різних рівнів складності ;

розвиваюча: сприяти розвитку логічного мислення, поширенню кругозору;

виховна: виховувати інтерес до математики, вміння працювати у групі, відповідальність перед товаришами.

Тип уроку: закріплення навичок та вмінь.

Обладнання: роздавальний матеріал для груп, правила проведення інтерактивної вправи «Мікрофон» та «Робота в малих групах» (пам’ятки), портрет К. Ф. Гауса, мікрофон, набір літер.

Епіграф уроку: «Математика – цариця наук, ….» Карл Фрідріх Гаус.

 

Хід уроку

1. Організаційний момент.

2. Мотивація навчальної діяльності  учнів:

На дошці ви бачите портрет німецького математика К. Ф. Гауса, сьогоднішній урок ми присвячуємо  цій видатній людині. У всій історії математики немає нікого, кого б можна було порівняти з Гаусом за ранньою обдарованістю. Він виявив її, коли йому не було й трьох років. Гаус згадував напівжартома, що вмів рахувати раніше, ніж навчився говорити. Якось у батька Карла зібралися товариші по роботі, щоб розподілити зароблені за тиждень гроші. Тут же був і трирічний Карл. Коли батько закінчив розрахунки, які він проводив уголос, і повідомив результати, Карл вигукнув: «Батьку, ти помилився!».  Присутні були вражені заявою маленької дитини, але батько перерахував спочатку, коли він назвав нову цифру, Карл радісно вигукнув: «Тепер правильно!». Найвідоміший його вислів є епіграфом до нашого уроку «Математика – цариця наук,…» але  ви помітили, що речення  є незакінченим. Кінець цієї фрази зашифрований, і тільки працьовиті, розумні і кмітливі в змозі розгадати її. Спробуємо це зробити?

3. Повідомлення теми та мети уроку.

Тема нашого уроку « Розв’язування   вправ   на   додавання   та  віднімання натуральних чисел». Наша мета: закріпити вміння додавати та віднімати натуральні числа, використовувати властивості додавання і віднімання під час розв’язування вправ,  розгадати вислів Гауса.

Але спочатку, згадаємо всі необхідні нам відомості. Проведемо інтерв’ю.

4. Актуалізація опорних знань. Інтерактивна вправа «Мікрофон».

Передаючи мікрофон діти згадують:

- натуральні числа – числа, які використовуємо при лічбі предметів;

- компоненти додавання: доданок + доданок = сума;

- компоненти віднімання: зменшуване - від’ємник = різниця;

- дії додавання і віднімання виконуємо по розрядам;

- щоб дізнатися на скільки одна величина більше другої, треба від більшої величини відняти меншу;

- від зміни місць доданків сума не змінюється; (переставний закон)

- для того, щоб до суми чисел додати третє число, можна до першого числа додати суму другого і третього чисел; (сполучний закон)

- якщо один з двох доданків дорівнює нулю, то сума дорівнює другому доданку;

- в сумі декількох чисел доданки можна змінювати місцями і об’єднувати їх в дужки будь  яким способом;

- для того щоб від числа відняти суму двох доданків, можна від цього числа відняти один з доданків, а потім від результату відняти другий доданок;

- для того щоб від суми двох доданків відняти число, можна відняти це число від одного з  доданків, а потім до результату додати другий доданок.

5. Колективне розв’язування вправ.

 Відомо, що в усних обчисленнях Гаусу не було рівних. З’ясуємо як ви вмієте рахувати. Питання по рядам.

1-й ряд:

10 яблук мав Данило,

і рум’яних  і красивих.

Якщо два із них він з’їсть.

То залишиться їх…(Не 6, а 8)

2-й ряд:

Думає вправно твоя голова:

П’ять плюс один, ти отримуєш…(Не 2, а 6)

3-й ряд:

Два апельсини було у Юрка.

Татко один ще купив для синка.

Довго тепер син не вийде з квартири.

Поки всі фрукти не з’їсть, всі…(Не 4, а 3)

 

 Бачу, що усно рахувати ви вмієте… Розв’яжемо складніше завдання:

- Обчислити суму всіх натуральних чисел від 1 до 100. Я розповім вам як зробив це Гаус, коли навчався у третьому класі: (1+100)+(2+99)+…+(50+51)= 50*101=5050

Хто з вас хоче уявити себе на місці маленького Гауса і розв’язати таку вправу:

- На скільки сума 1+3+5+…+99 менша від суми 2+4+6+…+100? (на 50)

Гаус вивів формулу для пасхалії – визначення дня святкування християнської Пасхи, розробив значну кількість методик обчислень, якими користуються і сьогодні представники багатьох професій: архітектори, токарі, фрезерувальники, слюсарі і т. д. Тому на його честь було виготовлено медаль, на якій зроблено напис «Король математики».

Прийшов час розгадати вислів Гауса, об’єднуємось у групи по 4 учні, розв’язуємо запропоновані вправи (кожній вправі відповідає літера), розташовуємо отримані відповіді у порядку спадання і знайдемо порядок в якому записані літери. Таким чином, кожна група знайде 4 літери, ми об’єднаємо їх із всіх груп та відтворимо таємний вислів.

6. Інтерактивна вправа «Робота в малих групах»

Завдання для першої групи: Обчислити, використавши властивості додавання і віднімання: 235+82+18+365             Ф        (1643+2759)-259            Р        54923-(6215+14623)      А        (913+798)-613                И	Завдання для другої групи: Обчислити, використавши властивості додавання і віднімання: 171+32+68+429                И         (2749+5164)-1349             Е         48583-(9217+2483)         М        (959+358)-459                   Т
Завдання для третьої групи: Обчислити, використавши властивості додавання і віднімання: 235+82+18+365             Ц        (1643+2759)-259            А        54923-(6215+14623)      К        (913+798)-613                -	Завдання для четвертої групи: Обчислити, використавши властивості додавання і віднімання: 171+32+68+429              Ц        (2749+5164)-1349           Р        48583-(9217+2483)         А        (959+358)-459                 И
Завдання для п’ятої групи: Обчислити, використавши властивості додавання і віднімання: 235+82+18+365              Т        (1643+2759)-259            М       54923-(6215+14623)      Я        (913+798)-613                А	Завдання для шостої групи: Обчислити, використавши властивості додавання і віднімання: 171+32+68+429                  Т         (2749+5164)-1349              М   48583-(9217+2483)            Е        (959+358)-459                    А
Завдання для сьомої групи: Обчислити, використавши властивості додавання і віднімання: 235+82+18+365             !          (1643+2759)-259            К        54923-(6215+14623)      И        (913+798)-613                И

Отже, отримали вислів «Математика – цариця наук, арифметика – цариця математики!»

 

7. Підведення підсумків та оцінювання учнів.

Рефлексія:

- Що нового дізналися на уроці?

- Чого навчилися?

- Чи згодні ви з висловом Гауса? Чому?

 

8. Повідомлення домашнього завдання (відповідно до підручника)

1. Обчислити , використавши властивості додавання і віднімання:

а) 635+72+28+365; б) (3497+2709)-209; в) 54923-(384+1623)

2. Як зміниться сума двох доданків, якщо:

а) перший доданок збільшили на 3;

б) перший доданок збільшили на 24, а другий - зменшили на 13;

3. Як зміниться різниця двох чисел, якщо:

а) зменшуване збільшити на 815;

б) від’ємник збільшити на 902;

в) зменшуване збільшити на 57, а від’ємник збільшити на 33?

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Урок № 8.

Тема. Віднімання натуральних чисел.

Мета: закріпити засвоєння учнями означення віднімання двох нату­ральних чисел, властивостей нуля під час віднімання та знання власти­востей віднімання натуральних чисел; завершити відпрацювання на­вичок застосування названих знань; перевірити рівень засвоєння навчального матеріалу.

Тип уроку: застосування знань, навичок та вмінь.

 

Хід уроку

І. Перевірка домашнього завдання.

 

Гра «Ланцюжок»

На дошці записано ланцюжок обчислень. Потрібно знайти число, яке стоїть в кінці ланцюжка обчислень.

 

1)

 

 

 

 

 

 

2)

 

 

 

 

ІІ. Актуалізація опорних знань

Усні вправи

1. Що означає відняти: 1) від 16 число 9; 2) число 12 від 19?
2. На скільки сума чисел 72 і 28 є більшою за їх різницю?
3. Серед виразів знайдіть рівні та обчисліть їх значення:

1) 24 – (14 + 7); 2) (24 – 14) – 7; 3) (24 + 17) – 14; 4) (24 – 14) + 17.

4. У п'ятому класі навчається 2 її хлопчик, що на 7 більше, ніж дівчаток. Скільки учнів у цьому класі?
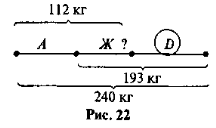
5. Яке найменування треба поставити замість ..., щоб рівність була пра­вильною?

1) 7 грн. 35 к. – 535 ... = 1 грн.;

2) 3 км 520 м + 2 480 ... = 6 км;

3) 15... 4т 200 кг =10 т 400...

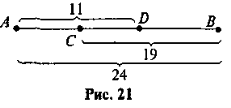
6. Знайдіть довжину відрізка CD (рис. 21).

 

IIІ. Відпрацювання навичок

 Оскільки увесь теоретичний матеріал теми викладено на попередніх двох уроках, то цей урок треба відвести під розв'язування різних видів вправ. Подальше відпрацювання навичок віднімання багатоцифрових на­туральних чисел продовжується у процесі розв'язання вправ 211 (7, 8) та 221 (1,3).

Розв'язування задач на віднімання на­туральних чисел. Можна запропонувати такі номери: № 226 (перед розв'язанням доречно буде знову звернутись до № 6 ус­них вправ і спробувати «намалювати» умо­ву задачі за допомогою відрізків (рис. 22)).

№ 228 є логічним продовженням задачі № 226.

Як варіант завдання на застосування властивостей віднімання для спрощення виразів можна запропонувати № 236 (1; 3; 6). Для досліджен­ня можна запропонувати учням скласти вираз і спростити його. (Ана-логічний№ 193 з попередньої теми.) Оформлення записів у зошитах учнів може бути таким:

№236

1) а – b — різниця; (а + 8) – b = (a – b) + 8 — нова різниця, отже, вона більша від (а – b) на 8.

Під час розгляду більш складних випадків (якщо відомі властивості не можна застосувати, доречно буде розглянути відповідні приклади).

 

IV. Закріплення знань учнів

Самостійна робота
Варіант 1

1. Обчисліть: 1) 65 015 – 8 249; 2) 300 000 – 217 157.
2. Знайдіть значення виразу, обираючи зручний порядок дій:

1) (547 + 195) – 147; 2) 358 – (158 + 317).

3. Розв'яжіть задачу. За три дні в магазині було продано 219 кг апель­синів. За перший день було продано 85 кг, що на 19 кг більше, ніж за другий. Скільки апельсинів було продано третього дня? В який день було продано найбільше апельсинів?
4. Спростіть вираз: 1) 95 – (х + 39); 2) (34 + х) – 16.

Варіант 2

1. Обчисліть: 1) 85 147 – 7 239; 2) 1 000 000 – 987 654.
2. Знайдіть значення виразу, обираючи зручний порядок дій:

1) (817 + 659) – 159; 2) 973 – (149 + 473).

3. Розв'яжіть задачу. Петрик, Василько та Миколка пішли рибалити. Ра­зом вони спіймали 195 рибок, причому Петрик спіймав 54 рибки, що на 15 більше, ніж Василько. Скільки риб спіймав Микола? Хто з хлопців найспритніший рибалка?

Спростіть вираз: 1) 104 – (х + 49); 2) (56 + х) – 28.

 

V. Домашнє завдання (відповідно до підручника)

 

 

 

                                                            Урок № 9.

Тема. Числові та буквені вирази. Формули.

Мета: сформувати уявлення учнів про поняття «числові вирази» та «бук­вені вирази»; навчити розпізнавати числові і буквені вирази, читати їх; виро­бити вміння знаходити значення виразів за умови різних значень змінної.

Тип уроку: засвоєння нових знань.

 

Хід уроку

І. Перевірка домашнього завдання.

 

ІІ. Актуалізація опорних знань

Усні вправи

1. Обчисліть: 1) 12 + 16; 2) 39 – 24; 3) 18 · 2; 4) 39 : 3; 5) 75 + (25 + 13);

6) 75 – (25 + 13); 7) (36 + 19) – 16; 8) (36 + 19) – 19; 9) (47 + 18) – (17 + 8).

2. Розв'яжіть задачу.

1) Поїзд йшов дві доби. За першу добу він пройшов 980 км, а за другу на 50 км більше. Скільки кілометрів проїхав поїзд за дві доби?

2) Поїзд йшов дві доби. За першу добу він пройшов 980 км, а за другу на 65 км більше. Скільки кілометрів проїхав поїзд за дві доби?

 

IІI. Формування нових знань

1. Поняття числового виразу

 Розглянувши розв'язання задач в п. 2 (1,2), усних вправ, учитель наголошує, що для розв'язання цих задач можна було скласти один запис (для кожної):

1) 980 + (980 + 50); 2) 980 + (980 + 65).

Кожний із таких записів (складається з чисел, знаків дій та дужок) на­зивається числовим виразом.

Якщо в числовому виразі виконати всі дії (в тому порядку, який відомий учням з початкової школи), то отримане число називається значен­ням числового виразу.

2. Читання числових виразів

 Уже з п'ятого класу слід привчати учнів читати вирази, використо­вуючи назви дій. Тому після введення поняття числового і буквеного виразу, вчитель повторює, що вирази, які містять знаки арифметичних дій, можна читати, використовуючи назви цих дій.

Приклад

Сума 7 і  а : 7 + а;

різниця 7 і а : 7 – а;

добуток 7 і суми 3 і а : 7 · (3 + а);

частка від ділення суми 7 і 3 на а : (7 + 3) : а.

3. Поняття буквеного виразу

Після введення поняття числового виразу та його значення учням за­пропоновано задачу 3.

Поїзд йшов 3 доби. За першу добу він пройшов 980 км, а за другу — на т кілометрів більше. Скільки кілометрів проїхав поїзд за 2 доби?

Питання до класу

• Чим схожа умова задачі 3) на задачі 1) і 2) (розв'язані перед цим в ус­них вправах)?
• Чим відрізняється умова задачі 3) від попередніх?
• Що спільного будуть мати вирази для розв'язання 3) і 1), 2)? А чим будуть відрізнятися ці записи?

(Однакові дії, пари для виконання дій і форма: 980 + (980 + т), але замість 50 і 65 маємо т.)

Зазначаємо, що якщо замінити т на числа 50 і 65, будемо мати розв'я­зання задач 1), 2), якщо інші числа — то розв'язання схожих задач.

Тобто маємо вираз 980 + (980 + т), який містить букву — буквений вираз.

Робота з підручником

Отже:

• числовими виразами називається ...;
• значення числового виразу називається...;
• буквеним виразом називається ...

 

IV. Закріплення знань, засвоєння вмінь

Вправи для письмового виконання

 

V. Домашнє завдання (відповідно до підручника)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

                                                                Урок № 10.

Тема. Числові та буквені вирази. Формули.

Мета: сформувати уявлення учнів про формули як ключ до розв'я­зання цілого класу задач; продовжувати формування вмінь учнів знаходи­ти значення буквених виразів, а також читати їх і складати буквені вирази за умовою задачі.

Тип уроку: засвоєння навичок та вмінь.

 

Хід уроку

І. Перевірка домашнього завдання.

 

Математичний диктант

1. Запишіть у вигляді числового виразу, скільки коштує покупка, якщо купили 15 ложок по 2 грн за штуку і 5 виделок по 3 грн за штуку [ 12 ло­жок по 3 грн за штуку і 7 виделок по 2 грн за штуку]. Яка вартість по­купки?
2. Запишіть вираз: а) добуток чисел 3 і 7 [5 і 9]; б) частка чисел 30 і 5 [50 і 10]; в) сума чисел 60 і добуток чисел 3 і 7 [сума числа 50 і добуток чисел 5 і 9].
3. Запишіть вираз і знайдіть його значення при зазначених числах:

а) різниця х і 15; х = 21 [13 і у; у = 7]; б) сума 2 і у; у = 19 [х і 3; х = 28];

в) b – b, b — будь-яке [а – 0, а — будь-яке].

 

II. Актуалізація опорних знань

Частково має місце під час виконання математичного диктанту. Але після виконання і перевірки завдань (можна завчасно проаналізувати правильні відповіді за дошкою або перевірити знання учнів, що викону­вали математичний диктант за дошкою) слід ще раз повторити основні моменти, розглянуті на попередньому уроці:

• означення числового виразу; т значення числового виразу;
• буквений вираз;
• як знайти значення буквеного виразу;
• як прочитати вираз, використовуючи назви арифметичних дій.

 

III. Формування нових знань

Розв'язати задачі за рисунками (рис. 23).

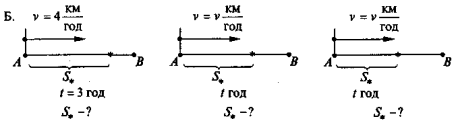
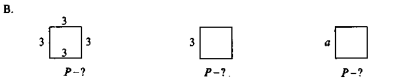
Рис. 23

При цьому на дошці і в зошитах учнів послідовно з'являються записи:

А. Р = 2(3 + 5);	Р = 2(3 + а);	Р = 2(а + b)
Б. S* = 4 · 3;	S* = v · 3;	S = vt
В. Р = 3 + 3 + 3 + 3;	Р = 4 · 3.	Р = 4а

 Після цього більшість учнів зрозуміли, що задачі кожної групи були схожі і відрізнялись тільки значенням величин, тобто записи, що містяться в останньому стовпчику, є загальним правилом, за яким мож­на розв'язувати задачі цього виду. Далі вводиться поняття формули (вивішується таблиця-схема).

Таблиця-схема «Формули. Вирази».

(У зошитах учні роблять запис. Формули S = v · t; P = 2(a + b); Р = 4а.)

Наголошується, що практично для розв'язання всіх задач можна скла­сти формулу; для цього треба тільки позначити всі величини, що названі в задачі буквами і записати план розв'язання задачі у вигляді рівності, в лівій частині якої — шукана величина, а в правій — буквений вираз.

Далі розглядаються приклади 1-3 з підручника.

Отже, щоб розв'язати задачу, можна скласти рівність, позначивши шу­кану величину буквою і прирівнявши її до складеного буквеного виразу.

 

IV. Закріплення знань. Формування вмінь. Розв'язування вправ

1. Знайдіть суму, різницю, добуток і частку чисел 20 і 5.
2. Суму чисел 13 і 17 збільшіть у 5 разів.
3. Різницю чисел 72 і 46 збільшіть на 14.
4. Чому дорівнює значення виразу 3х – 8, якщо: 1) х = 9; 2) х = 0?
5. Обчисліть значення у за формулою: у = х · х + 13, якщо: 1) х = 1; 2) x = 10.
6. Два равлики повзуть зі швидкістю 5 м/хв і 3 м/хв. З якою швидкістю вони віддаляються один від одного, якщо:

1) повзуть в одному на­прямку; 2) повзуть назустріч один одному?

7. Серед виразів знайдіть пари рівних і поясніть, чому вони рівні:

1) а + (b + с); 2) а – (b + с); 3) (а + b) – с; 4) (а – с) + b;

5) (а + с) + b; 6) (а – b) – с.

 

V. Домашнє завдання (відповідно до підручника)

 

 

 

 

Урок № 11. Тема. Розв’язування задач. Підготовка до контрольної роботи

Мета: систематизувати основні знання учнів про додавання і віднімання натуральних чисел; перевірити, як учні засвоїли теоретичний матеріал та як вміють застосовувати його на практиці; перевірити знання і уміння, набуті учнями під час вивчення тем «Натуральні числа», «Порівняння натуральних чисел», «Додавання і віднімання натуральних чисел»; оцінити досягнення кожного учня в опануванні перелічених тем; розвивати розумові операції, вміння аналізувати, порівнювати, узагальнювати, класифікувати, розмірковувати за аналогією; розвивати творче мислення; виховувати волю, почуття, духовні потреби і мотиви діяльності.

Обладнання: мультимедійна презентація, картки.

ХІД УРОКУ

1. «Вхід» в урок

 Реклама математики

 - Якщо ви дійсно хочете бути переможцем – урок математики для учнів, здатних потурбуватись про себе!

 - Змінюється все – досконалість математики незмінна! Відчуй задоволення від досконалості!

 - Понад 70 тисяч думок щодня! Відведи кілька з них на математику – і ти не пожалкуєш!

 - Математика – це там, де весело!

 - Тільки «Математика» - насолода та успіх!

Сьогодні на уроці ми з вами будемо продовжувати працюватися з натуральними числами. А чим саме ми будемо займатися на уроці, ви здогадаєтесь після виконання наступного завдання.

На дошці запис:

+;  ?;  -;  *.

<  ☼  >  ◊ =

 - Який із записаних знаків в І рядку зайвий? Чому?

 - Яку загальну назву мають знаки, що залишились? (Знаки математичних дій)

 - Які знаки зайві у ІІ рядку? Чому?

 - То чим ми сьогодні будемо займатися на уроці?

 - Виконувати дії з натуральними числами треба вміти для того, щоб розв’язувати практичні задачі в повсякденному житті, а також для подальшого вивчення математики й інших предметів: фізики, хімії, економіки тощо.

 - Для того, щоб добре виконувати дії над натуральними числами, треба постійно тренуватися. Ці тренування допоможуть вам успішно виконати контрольну роботу, а в старших класах ці вміння знадобляться і на екзаменах.

2. Актуалізація опорних знань

1. Прочитайте числа: 34 891,13 240, 10 101, 937 896, 1 342 789, 5 834 541, 1 001 102.

2. Інтелектуальна розминка

 - Продовж числовий ряд:    1, 3, 6, 10, 15, …(21, 28, 37, 47, 58, 70, …)

 - Поясніть закономірність, яка використана при побудові числового ряду.

 (+ 2, + 3, +4, і т.д.)

 3. Назвіть порядок дій: а) 32 + 204 ∙ (739 – 147) : 8;

б) (41 201 – 305 : 35) + 21 ∙ 3;

в) 4235 + (4121 : 21 – 42 ∙ 590).

3. Закріплення матеріалу

 №1. Виконайте дії:

а) 57369 + 2947 = 60 316

б) 97343 – 2089 = 95 254

в) 12323 + 3059 = 15 382

г) 5220 – 145 = 5075

д) 49 ∙ 23 + 3920 : 28 = 1127 + 140 = 1267

4. Усна колективна робота

 1. Обчислюємо ланцюжком

 2. Вкажіть в запропонованих  рядах чисел натуральний ряд:

1,  3,  5,  7… 0,  1,  2,  3… 1,  2,  3,  4…

 - Чому?

Які числа називаються натуральними? (Натуральними називаються числа, які використовуються при лічбі предметів. N — позначення множини натуральних чисел.)

 - Сформулюйте властивості ряду натуральних чисел. (1. Починається натуральний ряд з числа 1. Це число є найменшим числом натурального ряду. Найбільшого натурального числа не існує. 2. За кожним числом натурального ряду йде цілком визначене натуральне число. 3. Кожному числу натурального ряду, крім 1, передує цілком визначене натуральне число.)

 - Яке найменше і найбільше натуральне число? (Найменше натуральне число — одиниця, а найбільшого не існує.)

 3. Вкажіть число вісімнадцять мільйонів три тисячі сто сімдесят п’ять:

183 001 75

18 003 175

1 831 750 0

 4. Виберіть й вкажіть правильний варіант відповіді:

10 км. 15 м = ?

1015 м 

10 015 м 

10 150 м 

5. Закріплення матеріалу

 №2. Знайдіть значення числового виразу:

(9810 : 9 – 7560 : 7 + 290) ∙ 4  = 1200

1)  1090

2)  1080

3)  10

4)  300

5)  1200

 

6. Творчі завдання

 Розгадайте кросворд

			Д						К
			О		Ч		С		В
К	В	О	Д	Д	И	Н	А	Т	А
Л	І	Д	А	Е	С	А	Н	И	Д
А	Д	И	Н	С	Л	Т	Т	С	Р
С	Р	Н	О	Я	О	У	И	Я	А
	І		К	Т		Р	М	Ч	Т
	З			К		А	Е	А
	О			И		Л	Т
	К					Ь	Р
						Н
						І

1. Група з трьох цифр у запису   багатоцифрового числа.

2. Частина прямої, обмежена з двох сторін.

3. Найменше натуральне число.

4. Компонент дії додавання.

5. Назва другого розряду класу одиниць

6. Основне поняття в математиці.

7. Назва чисел, які використовуються при лічбі предметів.

8. Одиниця вимірювання довжини.

9. Найменше чотирицифрове число.

10. Чотирикутник, у якого всі сторони рівні.

7. Закріплення матеріалу

 №3 Розв’яжіть задачу. Вершник проїхав 80 км за 5 год.  Скільки  часу  витратить на  дорогу мотоцикліст, якщо його швидкість на 24 км/год більше, ніж швидкість вершника?

Розв’язання:

1)  80 : 5 = 16 (км/год) - швидкість вершника

2)  16 + 24 = 40 (км/год) - швидкість мотоцикліста

3)  80 : 40 = 2 (год)

Відповідь: 2 години витратить на дорогу мотоцикліст.

8. Усна колективна робота

1. Виберіть правильну відповідь, порівнявши числа.

815 771 > 816 331

815 771 < 816 331

815 771 = 816 331

2. Виберіть правильну відповідь, порівнявши величини.

5км 10м > 5000м 5км 10м < 5000м

5км 10м = 5000м

3. Виберіть правильну відповідь, порівнявши величини.

4год > 240хв 4год < 240хв

4год = 240хв

4. Знайди та виправ помилки в записах:

233  >  230 8247  <  8247 7777  =  77 777 12 015  > 12 105

5. Скільки трикутників на малюнку? (13)

9. Закріплення матеріалу

№3 Розв’яжіть задачу.  З   150 кг   молока отримують 6 кг масла. Скільки кілограмів молока знадобиться, щоб отримати 32 кг масла?

Розв’язання:

1)  150 : 6 = 25 (кг) - молока для 1 кг масла

2)  25 ∙ 32 = 800 (кг)

Відповідь: 800 кг  молока  знадобиться, щоб отримати  32 кг  масла.

 

12. Підсумок уроку

- Що на уроці було головним? Що було цікавим? Що нового сьогодні дізналися? Чому навчилися?

- Спасибі вам, діти, за урок!

 

13. Домашня робота (відповідно до підручника)

Завдання

1. Запиши цифрами числа:

а) двісті вісім тисяч шість;

б) тридцять мільйонів дві тисячі вісім;

в) чотириста вісім мільярдів три мільйони шість

2. Порівняй числа: а) 963123 і 964123; б) 9880987 і 9088 987.

3. Виконай дії: а) 74 025 + 18 994;    б) 2 456 369-324 157.                   

4.  Обчисли значення виразу:

а) 908 101 + 121 749-193 087;

б) 5 300 050 - 1 989 - 3 902 967.

5. Відніми від двох мільярдів:

а)  найбільше дев'ятицифрове число, всі цифри якого однакові;

б) найменше дев'ятицифрове число, всі цифри якого різні

6. Сума трьох доданків становить 78. Перший дода­нок дорівнює 50, другий - на 31 менший від нього. Знайди третій доданок

7. Як зміниться:    а) сума двох чисел, якщо один з доданків збіль­шити на 24, а інший - на 16;

б) різниця, якщо зменшуване збільшити на 17, а від'ємник збільшити на 10?

 

 

 

 

 

 

 

 

 

                                                          Урок № 12.

Тема. Додавання і віднімання натуральних чисел.

Мета: перевірити засвоєння учнями теми «Додавання і віднімання натуральних чисел. Вирази».

Тип уроку: перевірка та корекція знань, навичок та вмінь.

 

Хід уроку

І. Перевірка домашнього завдання.

Тематична контрольна робота

Варіант 1

1. Обчисліть: 1) 5 693 + 29 758; 2) 42 735 – 4 028.
2. На одній полиці було 47 книжок, що на 14 менше, ніж на другій, а на третій — на 17 книжок більше, ніж на першій. Скільки книжок було на трьох полицях разом?
3. Виконайте завдання, обираючи зручний порядок обчислення:

1) (228 + 453) + 772; 2) 163 + 236 + 364 + 237.

4. Перевірте, чи правильна нерівність:

1674 – (673 + 437) > 1885 – (648 + 664)?

5. Знайдіть значення т за формулою: т = 47 – 7t, якщо t = 5.
6. Спростіть вираз 389 + х + 211 і знайдіть його значення при х = 456.
7. Микола купив т олівців по 80 к. і 6 зошитів по п к. На скільки більше заплатив хлопчик за зошити, ніж за олівці? Складіть вираз і знайдіть значення отриманого виразу при т = 7, n = 95.
8. Знайдіть значення виразу, обираючи зручний порядок дій:

1) (913 + 798) – 613; 2) 252 – (96 + 152).

 

Варіант 2

1. Обчисліть: 1) 3 743 + 19 658; 2) 37 435 – 8 067.
2. На першій ділянці росло 52 дерева, що на 14 більше, ніж на другій, а на третій — на 19 менше, ніж на першій. Скільки дерев росло на трьох ділянках разом?
3. Виконайте додавання, обираючи зручний порядок дій:

1) (486 + 352) + 514; 2) 146 + 255 + 345 + 254.

4. Порівняйте, чи правильна нерівність:

6 011 – (1 539 – 438) < 5 791 – (2 418 – 1 336)?

5. Знайдіть значення а за формулою а = 4b + 7, якщо b = 19.
6. Спростіть вираз 257 + t + 143 і знайдіть його значення при t = 607.
7. Андрійко купив 14 конвертів по а к. та b марок по 80 к. На скільки більше заплатив хлопчик за марки, ніж за конверти? Складіть вираз та. обчисліть його значення, якщо а = 12, b = 1.
8. Знайдіть значення виразів, обираючи зручний порядок дій:

1) (959 + 358) – 459; 2) 879 – (458 + 179).

 

Контрольна робота у вигляді тестових завдань

 

Тестові завдання № 1

За кожне завдання – по 1 балу

1.    Яка цифра записана в розряді сотень числа 198546?

а) 9;               б) 8;             в) 5;               г) 4.

2.    Скільки мільйонів має число 3 208 003?

а) два;           б) нуль;   в) вісім;         г) три.

3.    Яке натуральне число передує числу 7100?

а) 7 009;        6)7 101;       в) 7 999;        г) 7 099.

4.    Яке найменше п'ятицифрове число можна записати цифрами 0 і 6?

а) 66 660;         б) 60 000;      в) 66 066;      г) 60 006.

5.    Яке з чисел найбільше: 13, 27, 55, 78, 44, 75, 31?

а) 55;             б) 44; в) 75;             г)78.

6.    Який знак треба поставити замість зірочки:

83 333*82 999?

а) >;               б) <;  в)=;               г)>.

7.    Які з чисел 100,60,20,180 є розв'язками нерівності х + 485 > 550?

а)100 і 20;     б) 100 і 180;         в) 60 і 100;    г) 20 і 60.

8.    Який корінь має рівняння х - 70 = 33?

а) 47;             6)37; в) 33;             г) 103.

За кожне завдання – по 2 бала

9.    Якому числу дорівнює сума чисел 5 311 і 498?

а) 5 809;        6)10 291; в) 5 709;        г) 5 889.

10. При якому значенні а рівність а +2а = 2а — а є правильною?

а) 1;   б) такого значення не існує;   в) 0;    г) 4.

 

Тестові завдання № 2

1. (1 б.) Запишіть цифрами число: вісім мільярдів дев’ять тисяч сім.

А) 897; Б)8 009 007;      В) 8 090 000 007;      Г) 8 000 009 007.

2. (1 б.) Яка цифра записана в розряді сотень класу тисяч у числі   456 178?

А) 1;  Б) 7;  В) 6;  Г) 4.

3. (1 б.) Який знак треба поставити замість зірочки  12 369 * 12 371?

А) >;   Б) <;    В) =;    Г) Визначити неможливо.

4. (1 б.) Запишіть найбільше чотирицифрове число, у запису якого використані цифри 7, 9, 1, 0, які не повторюються.

А) 7910;  Б) 1079;   В) 9710;   Г) 9701.

5. (1 б.) Яке з наведених чисел перетворює нерівність х + 42 < 654 на правильну числову нерівність?

А) 612;    Б) 418;   В) 615;    Г) 904.

6. (1 б.) Виконайте віднімання 33 000 251 – 6 691 893.

А) 26 308 358;    Б) 27 308 359;  В) 36 308 358;    Г) 26 308 359.

7. (1 б.) Розв’яжіть рівняння: х – 187 = 453.

А) 266;    Б) 267;    В) 640;    Г) 650.

8. (2 б.) Обчисліть значення виразу: 64 362 + 15 819 – 40 237.

А) 29 944;                 Б) 39 944;   В) 39 044;                 Г) 40 004.

9. (2б) У новому будинку 206 двокімнатних квартир, а трикімнатних – на 34 менше, ніж двокімнатних. Скільки двокімнатних і трикімнатних квартир у будинку?

А) 240;    Б) 446;    В) 172;    Г) 378.