Дії з десятковими дробами

Тема уроку: «Дії з десятковими дробами», 5 клас

Мета:

• Навчальна: формувати вміння застосовувати правила арифметичних дій з десятковими дробами на практиці; перевірка практичних навичок і вмінь при роботі з десятковими дробами; познайомити з історичною довідкою про дроби; використання Google форм для перевірки знань.
• Розвивальна: розвивати матиматичне мовлення; вміння аналізувати інформацію; активізувати роботу на уроці, вводячи елементи гри.
• Виховна: виховувати інтерес до вивчення математики; зацікавити до вивчення матеріалу.

Хід уроку:

1. Організаційний момент.

Перевірка домашнього завдання, заданого за підручником.

Історична довідка

      Десяткові дроби, як і звичайні, виникли на основі практичної потреби в торгівлі, будівництві тощо. Розвиток науки, техніки, промисловості, розширення торгівельних відносин вимагали дедалі складніших обчислень. Тому постало питання про спрощення дій з дробами. Так виникла поняття десяткового дробу.

      В Азії дроби застосували ще до нашої ери (ІІ ст. до н. е.). У XV столітті аль-Каші, астроном і математик із Самарканда, у своїй праці «Ключ до арифметики» (1427 р.) систематизував і значно розвинув знання про десяткові дроби. Він описав правила дій над десятковими дробами, а самі дроби зображав так: 7856/4769 (риска ставилася між цілою і дробовою частиною).

    У 1585 році нідерланський учений Сімон Стевін опублікував свою працю «Десятина» про десяткові дроби (те, що десяткові дроби відкрив аль-Кащі, європейці ще не знали), але запис, який запропонував Стевін, був незручним. Наприклад, десятковий дріб 56,987 він записував 56 9 8 7. Кому як знак, що розділяє цілу і дробову частини числа, запропонував математик з Шотландії Джон

Непер (1550-1617). Його математичні роботи були спрямовані на спрощення та впорядкування записів в арифметиці, алгебрі та тригонометрії. Але ще раніше кому застосува німецький учений Йоган Кеплер (1571-1630).

2. Актуалізація опорних знань.

Гра «Четвертий зайвий»

Яке слово зайве в ряду?

Одиниці, десятки, сотні, тисячі (тисячі – такого розряду одиниць не існує)
Прямокутник, куб, квадрат, трикутник (куб – об’ємна фігура)
Лінійка, циркуль, кут, транспортир (кут – не є геометричним інструментом)
Копійка, п’ядь, п’ятак, четвертак (п’ядь не є монетою.)
Відро, вершок, лікоть, сажень (відро – є мірою об’єму, а не довжини)

Гра «Виправ помилку»

За 5-6 хв. учні повинні виправити помилки. Виграє той, хто знайде більше помилок.

3,7 + 2,251 = 5, 951 

5,8 + 3,618 = 8,1418 (невірно, т.к. 5,8 + 3,618 = 9,418)

6,42 ^. 10 = 6,420 (невірно, т.к. 6,42 ? 10 = 64,2)

0,006 ^. 100 = 0,6

4,4 тис. = 44000 (невірно, т.к. 4,4 тис. = 4,4 ^. 1000 = 4400)

0,054 ^. 100 = 0,54 (невірно, т.к. 0,054 ^. 100 = 5,4)

8,3 – 4,7 = 44 (невірно, т.к. 8,3 – 4,7 = 3,6)

6,8 – 5,1 = 1,7

45,531 : 10 = 4,531

0,046 : 10 = 0,46 (невірно, т.к. 0,046 : 10 = 0,0046)

3.Відпрацювання вмінь і навичок

№1. Поділити учнів на чотири варіанти вивести завдання на екран або роздати картки. Учні записують лише відповіді в зошиті в стовпчик.

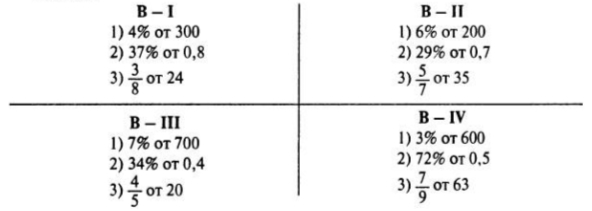
№2. Обчислити. Два учні записують відповіді на раніше записаних на дошці прикладах.

№3. Розв’язати рівняння. По черзі біля дошки розв’язують учні. Першого викликає вчитель, а учень потім визиває наступного за ним.

№4. Встановити залежність і заповнити пусту клітинку квадрата

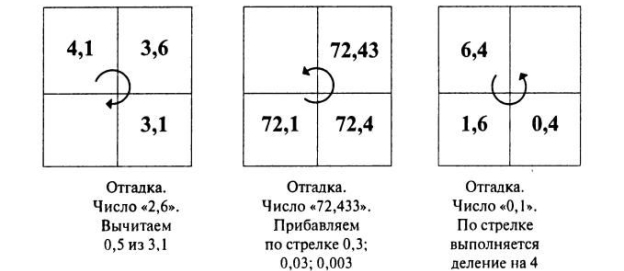
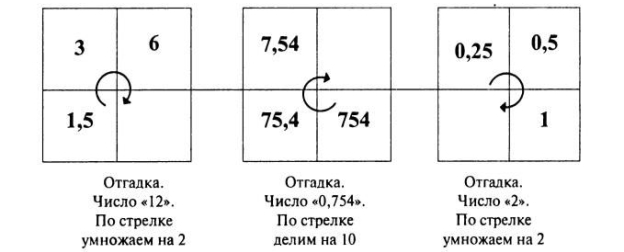
4. Підсумки уроку.

Я дізнався…

Я вмію… ж

Я хочу дізнатися…

Домашнє завдання:

Перейти за посиланням та виконати тестування в додатку Google форми

https://docs.google.com/forms/d/e/1FAIpQLSfJx4aB6l-daw1stGBPHfS_tPZSkN8hSWM2UaLOHyR9TsPSfA/viewform