Діагностичні роботи за групами результатів з алгебри 7 клас НУШ (за програмою О. Істера)
Діагностичні роботи з алгебри 7 клас НУШ за модельною програмою О. Істер. Також можна використати і для інших модельних програм.
Кожна робота містить по два рівнозначних варіанти.
Кожна робота поділена на три частини за групами результатів, оскільки кожен навчальний заклад вирішує як заповнювати журнал НУШ: в одній даті за діагностичну роботу оцінюють за кількома критеріями або в одній даті оцінка лише за одну групу результатів. Тому доцільно було б завдання діагностичних робіт частково виконати на самостійних роботах, уроках узагальнення. Оскільки, на мою думку, такий обсяг роботи неможливо оцінити за одну контрольну роботу, що також пропонують автори модельних програм В.Бевз та Н. Тарасенкова.
Оцінювання групи результатів 1 (ГР 1) Досліджує ситуації та створює математичні моделі - 2 завдання по 6 балів (в сумі 12 балів):
• наявність правильної відповіді – 1 бал;
• наявність математичної моделі (виразу, порядку дій) – 2 бали;
• правильне виконання дій – 1 бал;
• наявність пояснення до кожної дії – 1 бал;
• раціональність виконання моделі (якщо учень використав нестандартне рішення) – 1 бал.
Оцінювання групи результатів 2 (ГР 2) Розв`язує математичні задачі – 6 завдань (іноді 5-7) по 2 бали (в сумі 12 балів):
• наявність правильної відповіді – 1 бал;
• наявність запису виконаних дій – 1 бал.
Оцінювання групи результатів 3 (ГР 3) Інтерпретує та критично оцінює результати – 3 завдань (іноді 2-4) по 4 бали (в сумі 12 балів):
• наявність правильної відповіді – 1 бал;
• правильне виконання дій – 1 бал;
• наявність пояснення до кожної дії – 1 бал;
• наявність оцінки результатів – 1 бал.
Алгебра 7 клас
Діагностична робота № 1 «Повторення за курс 5-6 класу»
Діагностична робота № 2 «ЛІНІЙНІ РІВНЯННЯ З ОДНІЄЮ ЗМІННОЮ»
Діагностична робота № 3 «ЦІЛІ ВИРАЗИ. СТЕПІНЬ ІЗ НАТУРАЛЬНИМ ПОКАЗНИКОМ. ОДНОЧЛЕНИ»
Діагностична робота № 4 «МНОГОЧЛЕНИ»
Діагностична робота № 5 «ФОРМУЛИ СКОРОЧЕНОГО МНОЖЕННЯ»
Діагностична робота № 6 «ФУНКЦІЇ»
Діагностична робота № 7 «СИСТЕМИ ЛІНІЙНИХ РІВНЯНЬ З ДВОМА
ЗМІННИМИ»
Підсумкова діагностична робота № 8
Діагностична робота № 1 «Повторення за курс 5-6 класу»
Варіант 1
Потрібно дослідити задачу і виконати її з поясненням кожної дії
1. На координатній площині побудувати точки Р(2;4); К(–4; 3) і М(–2; 0). Проведіть пряму МК. Через точку Р проведіть пряму, паралельну до МК, і пряму, перпендикулярну до МК.
2. У великому бідоні було в 3 рази більше молока, ніж у малому. Коли з великого бідона відлили 29 л молока, а з маленького бідона відлили 3 л, то в обох бідонах молока стало порівну. Скільки літрів молока було в кожному бідоні спочатку?
ГР-2 Виконати завдання
1. Обчисліть: - 4 – ( - 8,5 + 5,3)
2. Спростіть вираз -4х(-6у-30-12х
3. Знайдіть значення виразу 9a-5/b, якщо a=1/8 b=8 4. Знайдіть корінь рівняння 5x+0.7=4x-3.4 .
5. Знайдіть невідомий член пропорції c:7=8:9.
6. Скільки відсотків від числа 36 становить число 27?
ГР-3 Потрібно проаналізувати вихідні дані та певну вимогу до завдання, розв’язати одержану задачу та записати її розв’язання з поясненням чи обґрунтуванням Упаковка містить 2/5 кг цукерок.
1) Мама на день народження Оленки купила для її друзів 15 упаковок цукерок. Скільки кілограмів цукерок купила мама?
2) Скільки знадобиться таких упаковок цукерок, щоб насипати в порожній мішечок 4 кг цукерок?
3) У ящику поміщається 10 кг цукерок. За день продали 17 упаковок. Скільки кілограмів цукерок залишилося?
одержав по 1/3 кг цукерок? (1 бал)
Діагностична робота № 1 «Повторення за курс 5-6 класу»
Варіант 2
Потрібно дослідити задачу і виконати її з поясненням кожної дії
1. На координатній площині побудувати точки А(2; 5); В(–1; 2) і С(3; 0). Проведіть пряму АВ. Через точку С проведіть пряму, паралельну до АВ, і пряму, перпендикулярну до АВ.
2. У першій діжці було в 4 рази більше води, ніж у другій. Коли з першої діжки відлили 27 л води, а в другу долили 15 л, то в обох діжках води стало порівну. Скільки літрів води було в кожній діжці спочатку?
ГР-2 Виконати завдання
1. Обчисліть: - 5 – ( - 7,3 + 5,1)
2.Спростіть вираз -2a(-5b+4)+8a
3. Знайдіть значення виразу 7x-5:y , якщо x=1/4 y=4
4. Знайдіть корінь рівняння 7x+0.9=6x-2.7.
5. Знайдіть невідомий член пропорції a:6=3:7 .
6. Скільки відсотків від числа 25 становить число 20?
ГР-3Потрібно проаналізувати вихідні дані та певну вимогу до завдання, розв’язати одержану задачу та записати її розв’язання з поясненням чи обґрунтуванням Упаковка містить 4/25 кг льодяників.
1) Сергійко з друзями купили 10 упаковок льодяників. Скільки кілограмів льодяників купили хлопці?
2) Скільки знадобиться таких упаковок льодяників, щоб насипати в порожній мішечок 4 кг льодяників?
3) У коробці поміщається 9,6 кг льодяників. За день продали 35 упаковок. Скільки кілограмів льодяників залишилося? (
4) Скільки потрібно взяти повних упаковок льодяників, щоб кожний із чотирьох друзів Сергійка одержав по 4/5 кг цукерок?
2 «ЛІНІЙНІ РІВНЯННЯ З ОДНІЄЮ ЗМІННОЮ»
Варіант 1
Потрібно дослідити задачу і виконати її з поясненням кожної дії 1. Перший автомобіль долає шлях між містами за 5 год. Другий автомобіль, швидкість якого на 20 км/год більша, ніж першого, долає той самий шлях за 4 год. Знайдіть швидкість автомобілів.
2.У книжковій шафі було в 6 разів більше книжок, ніж на етажерці. Після того як із шафи взяли 46 книжок, а з етажерки 18, на етажерці залишилося на 97 книжок менше, ніж у шафі. Скільки книг було в шафі, а скільки на етажерці спочатку?
ГР-2 Виконати завдання
1. Укажіть число, яке є коренем рівняння 3х–5=10:
2. Укажіть кількість коренів рівняння х+8=х:
3. Сполучіть кожне рівняння з відповідним коренем стрілкою:
4. Розв’яжіть рівняння 5х–12=3х+1:
5. Знайдіть значення змінної, для якої рівні вирази 0,6–х і 2,8+0,1х.
6. Розв’яжіть рівняння 
ГР-3 Потрібно проаналізувати вихідні дані та певну вимогу до завдання, розв’язати одержану задачу та записати її розв’язання з поясненням чи обґрунтуванням
Марія вирішила зайнятися вирощуванням квітів на продаж. Вона купила 12 горщиків з насінням, вартість одного горщика становить 45 гривень. Марія планує продати квіти так, щоб заробити на 30% більше, ніж витратила на покупку горщиків.
1. Скільки грошей витратила Марія на покупку всіх горщиків?
2. Яку суму грошей вона планує заробити після продажу квітів, враховуючи бажаний прибуток?
3. Якою повинна бути ціна одного горщика з квітами, щоб досягти запланованого прибутку?
2 «ЛІНІЙНІ РІВНЯННЯ З ОДНІЄЮ ЗМІННОЮ»
Варіант 2
Потрібно дослідити задачу і виконати її з поясненням кожної дії
1. Перший автомобіль долає шлях між двома містами за 1,5 год, а другий — за 1,2 год. Швидкість другого автомобіля більша від швидкості першого на 15 км/год Знайдіть відстань між милами.
2. В автопарку було вантажівок у 5 разів більше, ніж легкових автомобілів. Після того як у рейс вийшло 58 вантажівок і 15 легкових авто, в автопарку залишилось вантажівок на 61 більше, ніж легкових авто. Скільки легкових авто і скільки вантажівок було в автопарку спочатку?
ГР-2 Виконати завдання
1. Укажіть число, яке є коренем рівняння 3х+2=11:
2. Укажіть кількість коренів рівняння х+15 = х+15:
3. Сполучіть кожне рівняння з відповідним коренем стрілкою:
4. Розв’яжіть рівняння 7х+3=5х–4:
5. Знайдіть значення змінної, для якої рівні вирази 2,3–0,5х і 4,9+0,8х.
6. Розв’яжіть рівняння 
ГР-3 Потрібно проаналізувати вихідні дані та певну вимогу до завдання, розв’язати одержану задачу та записати її розв’язання з поясненням чи обґрунтуванням
Іван вирішив зібрати кошти для купівлі нового велосипеда, вартість якого становить 3000 грн. Щотижня він відкладає по 200 грн.
1. За скільки тижнів Іван збере необхідну суму?
2. Скільки грошей Іван збере за 10 тижнів?
3. Якщо Івану потрібно зібрати всю суму за 12 тижнів, скільки він повинен відкладати щотижня?
3 «ЦІЛІ ВИРАЗИ. СТЕПІНЬ ІЗ НАТУРАЛЬНИМ ПОКАЗНИКОМ. ОДНОЧЛЕНИ»
Варіант 1
ГР-1 Потрібно дослідити задачу і виконати її з поясненням кожної дії
1. На першій полиці стоїть а книжок, на другій — утричі більше, ніж на першій, а на третій — на 17 книжок менше, ніж на першій і другій полицях разом. Запишіть у вигляді виразу кількість книжок на трьох полицях разом. Обчисліть при а = 20.
2. Спростіть вирази :
2
1) 
2cd2
3
ГР-2 Виконати завдання
1. Знайдіть значення виразу –4х–2, якщо х= –4:
2. Укажіть вираз, що тотожно дорівнює виразу –12у+6–8у:
3. Знайдіть периметр прямокутника, якщо одна його сторона дорівнює а см, а друга сторона на 4 см менша:
4. Знайдіть значення виразу –2х4+5х2, якщо х=2
5. Запишіть у вигляді степеня вираз (х2)4 ∙ х3 :
6. Запишіть у стандартному вигляді одночлен (–2ab)3 ∙ 3а2b4 :
ГР-3 Потрібно проаналізувати вихідні дані та певну вимогу до завдання, розв’язати одержану задачу та записати її розв’язання з поясненням чи обґрунтуванням
Фермер вирощує овочі та фрукти на своєму полі. Він посадив:
• x гектарів картоплі,
• 2x+5 гектарів моркви, 3x−2 гектарів капусти.
1. Яка загальна площа поля, відведена під картоплю, моркву та капусту? Запишіть відповідь у вигляді одночлена.
2. Якщо площа під картоплю складає 10 гектарів, знайдіть площу, відведену під кожну культуру, та загальну площу.
3. Усі овочі фермер збиратиме з поля трактором, який може обробляти 5 гектарів за день. За скільки днів фермер обробить усе поле?
3 «ЦІЛІ ВИРАЗИ. СТЕПІНЬ ІЗ НАТУРАЛЬНИМ ПОКАЗНИКОМ. ОДНОЧЛЕНИ»
Варіант 2
ГР-1 Потрібно дослідити задачу і виконати її з поясненням кожної дії
1. За перший день магазин продав b кг цукру, за другий — на 58 кг більше, ніж за перший, а за третій — на 12 кг менше, ніж за другий. Запишіть у вигляді виразу кількість кілограмів цукру, проданого магазином за три дні. Обчисліть при b = 45.
2. Спростіть вирази:
1) 8х7у5 ∙ (-0,5х5у2)3; 2) 3
3с5d2 2c3d33
8 3
ГР-2 Виконати завдання
1. Знайдіть значення виразу 7х–9, якщо х= –4:
2. Укажіть вираз, що тотожно дорівнює виразу 15у–3+4у:
3. Знайдіть периметр прямокутника, якщо одна його сторона дорівнює а см, а друга сторона на 4 см більша:
4. Знайдіть значення виразу х2–3х3, якщо х=2
5. Запишіть у вигляді степеня вираз (х3)2 ∙ х4 :
6. Запишіть у стандартному вигляді одночлен 2а5b3 ∙ (–3ab)2 :
ГР-3 Потрібно проаналізувати вихідні дані та певну вимогу до завдання, розв’язати одержану задачу та записати її розв’язання з поясненням чи обґрунтуванням
Олена вирішила вирощувати квіти на своєму дачному полі. Вона купила кілька видів квітів і підготувала для них грядки прямокутної форми. Довжину кожної грядки вона позначила через a метрів, а ширину — через b метрів. Окрім цього, вона висаджує кущі троянд, і кожен кущ займає площу, рівну c квадратних метрів.
1. Скільки квадратних метрів займають усі грядки, якщо Олена створила n однакових грядок?
2. Скільки квадратних метрів Олені залишиться для інших рослин на ділянці, якщо загальна площа ділянки дорівнює S квадратних метрів?
3. Скільки кущів троянд Олена зможе посадити на решті ділянки?
Діагностична робота № 4 «МНОГОЧЛЕНИ»
Варіант 1
Потрібно дослідити задачу і виконати її з поясненням кожної дії
1. Доведіть, що вираз 165 – 86 ділиться на 3.
2. Знайдіть 4 послідовних натуральних числа, якщо відомо, що добуток третього та четвертого чисел більший від добутку першого та другого на 34.
ГР-2 Виконати завдання
1. Зведіть подібні члени многочлена 
.
2. Спростіть вираз 
.
3. Знайдіть значення многочлена 
.
4. Знайдіть добуток одночлена 
.
5. Виконайте множення многочлена на многочлен: 
.
6. Розв’яжіть рівняння 
.
ГР-3 Потрібно проаналізувати вихідні дані та певну вимогу до завдання, розв’язати одержану задачу та записати її розв’язання з поясненням чи обґрунтуванням
Фермер Петро вирішив засадити своє поле картоплею та морквою. Поле має форму прямокутника, причому довжина довшої сторони на 3 метри більша за довжину коротшої сторони. Якщо коротшу сторону позначити через x, то площу поля можна виразити за допомогою многочлена. Задача полягає у правильному розподілі площі між картоплею та морквою. 1. Запишіть вираз для площі поля у вигляді многочлена через змінну x.
2. Якщо відомо, що фермер виділив під картоплю площу x2+2x квадратних метрів, то скільки квадратних метрів він виділив під моркву? Запишіть вираз для цієї площі через x.
3. Знайдіть площу всього поля, якщо коротша сторона дорівнює 5 метрів.
Діагностична робота № 4 «МНОГОЧЛЕНИ»
Варіант 2
Потрібно дослідити задачу і виконати її з поясненням кожної дії 1. Доведіть, що вираз 274 – 95ділиться на 8.
2.Знайдіть 4 послідовних натуральних числа, якщо відомо, що добуток другого та четвертого чисел більше за добуток першого і третього на 31.
ГР-2 Виконати завдання
1. Зведіть подібні члени многочлена 
.
2. Спростіть вираз 
.
3. Знайдіть значення многочлена 
.
4. Знайдіть добуток одночлена 
.
5. Виконайте множення многочлена на многочлен: 
.
6. Розв’яжіть рівняння 
.
ГР-3 Потрібно проаналізувати вихідні дані та певну вимогу до завдання, розв’язати одержану задачу та записати її розв’язання з поясненням чи обґрунтуванням
Майстер Андрій виготовляє дерев’яні ящики для зберігання овочів. Він використовує різні види деревини, і кожний вид має свою вартість. Для замовлення одного ящика потрібно врахувати вартість матеріалів та роботи, які описуються многочленом.
Многочлен, який описує загальну вартість матеріалів для одного ящика, має вигляд: P(x)=5x2+3x+2,де x – кількість одиниць матеріалу, а вираз P(x)=5x2+3x+2 – загальна вартість виготовлення одного ящика.
1. Питання 1: Якою буде загальна вартість матеріалів, якщо для виготовлення одного ящика використано 4 одиниці матеріалу?
2. Питання 2: Якщо загальна вартість матеріалів не повинна перевищувати 100 гривень, скільки одиниць матеріалу може використати Андрій для виготовлення одного ящика?
3. Питання 3: Складіть многочлен для загальної вартості виготовлення трьох таких ящиків і знайдіть вартість, якщо для кожного з них було використано 3 одиниці матеріалу.
Діагностична робота № 5 «ФОРМУЛИ СКОРОЧЕНОГО МНОЖЕННЯ»
Варіант 1
Потрібно дослідити задачу і виконати її з поясненням кожної дії
1. Доведіть, що:
1) при будь-якому цілому n значення виразу (2п + 3)2 – (2п – 3)(2п + 5) ділиться на 8; 2) 220 + 225 – 411 ділиться на 29.
2. Доведіть, що різниця квадратів двох цілих чисел, взятих через 1, ділиться на 4.ГР-2 Виконати завдання
1. Винесіть спільний множник за дужки: 
.
2. Подайте у вигляді добутку многочлен 
.
3. Розкладіть многочлен 
на множники.
4. Розкладіть многочлен 
на множники.
5. Подайте тричлен 
у вигляді квадрата двочлена.
6. Розкладіть на множники двочлен 
.
ГР-3 Потрібно проаналізувати вихідні дані та певну вимогу до завдання, розв’язати одержану задачу та записати її розв’язання з поясненням чи обґрунтуванням
На дачі у пані Олени є два квітники, один квадратної форми, а другий прямокутний.
• Знайдіть вираз для площі квадратного квітника,
• Знайдіть вираз для площі прямокутного квітника,
• Якою буде різниця між площею квадратного квітника та площі прямокутного квітника?
Діагностична робота № 5 «ФОРМУЛИ СКОРОЧЕНОГО МНОЖЕННЯ»
Варіант 2
Потрібно дослідити задачу і виконати її з поясненням кожної дії
1. Доведіть, що:
1) при кожному цілому к значення виразу (k + 5)( k 2 – к + 1) - k(k + 2)2 + 3 ділиться на 8;
2) значення виразу 825 – 6412 ділиться на 7.
2. Доведіть, що різниця квадратів двох послідовних цілих чисел є непарним числом
ГР-2 Виконати завдання
1. Винесіть спільний множник за дужки: 
.
2. Подайте у вигляді добутку многочлен 
.
3. Розкладіть многочлен 
на множники.
4. Розкладіть многочлен 
на множники.
5. Подайте тричлен 
у вигляді квадрата двочлена.
6. Розкладіть на множники двочлен 
.
ГР-3 Потрібно проаналізувати вихідні дані та певну вимогу до завдання, розв’язати одержану задачу та записати її розв’язання з поясненням чи обґрунтуванням Андрій хоче облаштувати спортивний майданчик у дворі. Він планує встановити два прямокутні тренувальні майданчики різних розмірів.
• Перший майданчик матиме розміри a+ba + ba+b метрів завдовжки та a−ba - ba−b метрів завширшки.
• Другий майданчик буде квадратним, з довжиною сторони a+ba + ba+b метрів.
• Щоб обидва майданчики мали однакову площу, Андрій планує зменшити площу другого майданчика на площу прямокутної ділянки з розмірами a−ba - ba−b на b метрів, яка буде відділена для зони відпочинку.
1. Яка площа першого майданчика?
2. Яка площа другого майданчика?
3. Яку площу потрібно відокремити для зони відпочинку, щоб площі обох майданчиків зрівнялися?
Діагностична робота № 6 «ФУНКЦІЇ»
Варіант 1
Потрібно дослідити задачу і виконати її з поясненням кожної дії
1º. Функцію задано формулою у = -2х + 7. Визначте:
1) значення функції, якщо значення аргументу дорівнює 6; 2) значення аргументу, при якому значення функції дорівнює -9; 3) чи проходить графік функції через точку А (-4; 15).
2°. Побудуйте графік функції у = 3х – 2. Користуючись графіком, знайдіть:
1) значення функції, що відповідає аргументу 2;
2) значення аргументу, при якому значення функції дорівнює -5;
3) при яких значеннях аргументу функція набуває додатних значень?
ГР-2 Виконати завдання
1. Знайдіть значення функції 
, якщо значення аргументу x дорівнює –2.
2. При якому значенні аргументу значення функції 
дорівнює 5?
3. Побудуйте графік функції 
?
4. Запишіть координати точки, що належить графіку функції 
,
5. Знайдіть область визначення функції: 
.
6. Запишіть приклад формули лінійної функції?
ГР-3 Потрібно проаналізувати вихідні дані та певну вимогу до завдання, розв’язати одержану задачу та записати її розв’язання з поясненням чи обґрунтуванням
Андрій планує зробити ремонт у своїй квартирі та хоче пофарбувати стіни в новий колір. Йому потрібно купити фарбу, яка продається в банках певного об'єму. Щоб не переплатити, він хоче розрахувати, скільки банок фарби йому потрібно.
Вихідні дані:
• Відомо, що площа всіх стін, які Андрій хоче пофарбувати, дорівнює S квадратних метрів.
• Одна банка фарби покриває P квадратних метрів. Кожна банка коштує C гривень.
Напишіть функцію, яка розрахує загальну вартість фарби для всього ремонту. Функція приймає на вхід площу стін, площу, яку покриває одна банка, та ціну банки.
1. Скільки банок фарби знадобиться, щоб пофарбувати всі стіни?
2. Скільки гривень витратить Андрій на всю фарбу?
3. Якщо кожна банка фарби покриває на 10% менше площі, скільки банок буде потрібно в такому випадку?
Діагностична робота № 6 «ФУНКЦІЇ»
Варіант 2
ГР-1 Потрібно дослідити задачу і виконати її з поясненням кожної дії
1º. Функцію задано формулою у = 8х – 3. Визначте:
1) значення функції, якщо значення ар¬гументу дорівнює 2; 2) значення аргументу, при якому зна¬чення функції дорівнює -19; 3) чи проходить графік функції через точку В (-2; -13)?
2°. Побудуйте графік функції у = -2х + 5. Користуючись графіком, знайдіть:
1) значення функції, що відповідає ар¬гументу 2;
2) значення аргументу, при якому зна¬чення функції дорівнює -1;
3) при яких значеннях аргументу функція набуває від'ємних значень?
ГР-2 Виконати завдання
1. Знайдіть значення функції 
, якщо значення аргументу x дорівнює –3.
2. При якому значенні аргументу значення функції 
дорівнює 3?
3. Побудуйте зображено графік функції 
?
4. Запишіть координати точки, що належить графіку функції 
.
5. Знайдіть область визначення функції 
.
6. Запишіть приклад формули лінійної функції?
ГР-3 Потрібно проаналізувати вихідні дані та певну вимогу до завдання, розв’язати одержану задачу та записати її розв’язання з поясненням чи обґрунтуванням
Андрій вирішив відслідковувати свої витрати на їжу протягом місяця. Він веде облік витрат, де зазначає, скільки грошей витрачає на обід і вечерю щодня. Андрій помітив, що витрати на обід є сталими і становлять 80 гривень, а витрати на вечерю коливаються залежно від дня.
1. Якщо Андрій хоче дізнатися, скільки грошей він витрачає на обід за 30 днів, яка функція допоможе йому це обчислити?
2. Яка формула буде виглядати, якщо витрати на вечерю в середньому становлять 100 гривень на день, а загальні витрати на їжу в місяць можна виразити через функцію?
3. Як зміниться загальна сума витрат, якщо витрати на вечерю збільшаться до 120 гривень на день?
Діагностична робота № 7 «СИСТЕМИ ЛІНІЙНИХ РІВНЯНЬ З ДВОМА ЗМІННИМИ»
Варіант 1
ГР-1 Потрібно дослідити задачу і виконати її з поясненням кожної дії
1º Розв'яжіть задачу, склавши систему із двома змінними.
Із двох селищ одночасно назустріч одне одному вийшли два пішоходи й зустрілися через 3 години. Відстань між селищами 30 км. Один з пішоходів подолав до зустрічі на 6 км більше за іншого. Знайдіть швидкість кожного пішохода.
2°. У двох ящиках лежать яблука. Якщо з одного ящика перекласти до другого 45 яблук, то в обох ящиках яблук стане порівну. Якщо з другого ящика перекласти до першого 20 яблук, то в першому яблук стане утричі більше, ніж у другому. Скільки яблук було в кожному ящику? ГР-2 Виконати завдання
1. Яка пара чисел є розв’язком рівняння 
?
2. У рівнянні 
виразіть змінну x через змінну y.
3. 
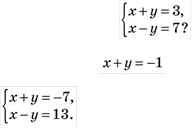Яка пара чисел є розв’язком системи рівнянь
4. Зазначте точку перетину графіка рівняння з віссю Ox.
5. Розв’яжіть систему рівнянь
6. Знайдіть число c, якщо графік рівняння 
проходить через точку 
.
ГР-3 Потрібно проаналізувати вихідні дані та певну вимогу до завдання, розв’язати одержану задачу та записати її розв’язання з поясненням чи обґрунтуванням
Аня і Маша допомагали мамі ліпити пиріжки. Якби Аня зліпила на 5 пиріжків більше, то у неї було б удвічі більше, ніж у Маші, а якщо б на 4 менше, то удвічі менше, ніж у Маші.
1) Яка пара чисел (х;у) задовольняє умову задачі, якщо х шт. – зліпила Аня, а у шт. – зліпила Маша?
2) Скільки пиріжків зліпила Аня і скільки Маша? Скласти задачу та розв’язати її.
3) Хто і на скільки більше зліпив пиріжків наступного дня, якщо вони працювали з такою ж продуктивністю і зліпили разом 52 пиріжки?
Діагностична робота № 7 «СИСТЕМИ ЛІНІЙНИХ РІВНЯНЬ З ДВОМА ЗМІННИМИ»
Варіант 2
ГР-1 Потрібно дослідити задачу і виконати її з поясненням кожної дії
1º. Розв'яжіть задачу, склавши систему рівнянь.
Із двох міст, відстань між якими 53 км, одночасно виїхали назустріч один одному два велосипедисти й зустрілись через 2 години. Знайдіть швидкість кожного
велосипедиста, якщо відомо, що другий велосипедист долає за 3 год на 18 км більше, ніж перший за 2 год.
2°. На будівництві працюють 50 малярів і теслярів. Через певний час кількість малярів збільшилась удвічі, а теслярів — утричі, і тепер кількість усіх робітників становить
130 осіб. Скільки було малярів і теслярів спочатку?
ГР-2 Виконати завдання
1. Яка пара чисел є розв’язком рівняння 
?
2. У рівнянні 
виразіть змінну y через змінну x.
3. 
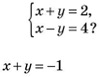Яка пара чисел є розв’язком системи рівнянь
4. Укажіть точку перетину графіка рівняння з віссю Oy.
5. Розв’яжіть систему рівнянь 
6. Знайдіть число k, якщо графік рівняння 
проходить через точку 
.
ГР-3 Потрібно проаналізувати вихідні дані та певну вимогу до завдання, розв’язати одержану задачу та записати її розв’язання з поясненням чи обґрунтуванням
Для посадки помідорів мама виділила ділянку прямокутної форми. Коли Артем додав довжини трьох її сторін, то отримав 21м, а коли Мілана додала довжини трьох інших сторін, то отримала 18м. Які розміри ділянки?
1) Яка пара чисел задовольняє умову задачі?
2) Обчислити периметр і площу ділянки.
3) Скласти математичну модель задачі та розв’язати її.
Підсумкова діагностична робота № 8
Варіант 1
ГР-1 Потрібно дослідити задачу і виконати її з поясненням кожної дії
1º За 7 кг апельсинів та 4 кг лимонів заплатили 26 грн. Скільки коштує 1 кг апельсинів та 1 кг лимонів, якщо 5 кг апельсинів дорожчі за 2 кг лимонів на 4 грн?
2°. 3 двох міст, відстань між якими 650 км, виїжджають назустріч один одному два потяги. Якщо потяги виїдуть одночасно, то вони зустрінуться через 10 год. Якщо перший потяг вирушить на 4 год 20 хв раніше від другого, то зустріч відбудеться через 8 год після відправлення другого. Яка швидкість кожного потяга?
ГР-2 Виконати завдання
1. Подайте у вигляді добутку вираз x x 3 5 x3 .
2. Знайдіть значення функції y x 5 2, якщо значення аргументу дорівнює 2.
3. Укажіть вираз, який тотожно дорівнює виразу p q2 2.
4. Запишіть у стандартному вигляді одночлен 3a b2 3 2a b3 2.
5. Укажіть кількість коренів рівняння x 10 x 1.
6. Обчисліть значення виразу 32 22 42.
ГР-3 Потрібно проаналізувати вихідні дані та певну вимогу до завдання, розв’язати одержану задачу та записати її розв’язання з поясненням чи обґрунтуванням
На шкільному ярмарку продаються печиво та цукерки. Вартість одного пакету печива становить 20 гривень, а одного пакету цукерок – 15 гривень.
1. Якщо Марія купила x пакетів печива і y пакетів цукерок, і витратила 300 гривень, складіть рівняння, що описує цю ситуацію.
2. Якщо Марія купила на 3 пакети цукерок більше, ніж пакетів печива, складіть ще одне рівняння для цієї ситуації.
3. Які значення x та y задовольняють обидва рівняння? Скільки пакетів печива і скільки пакетів цукерок купила Марія?
Підсумкова діагностична робота № 8
Варіант 2
ГР-1 Потрібно дослідити задачу і виконати її з поясненням кожної дії
1º. За 9 ручок і 4 олівці заплатили 4 грн 20 к. Скільки коштує одна ручка та один олівець, якщо дві ручки дорожчі за 3 олівці на 35 копійок?
2°. Із двох міст, відстань між якими 420 км, виїхали назустріч один одному два автомобілі. Якщо автомобілі вирушають одночасно, то вони зустрінуться через 4 год. Якщо перший автомобіль вирушить на 4 год 12 хв раніше за другого, то зустріч відбудеться через 2 год після виїзду другого. Яка швидкість кожного автомобіля?
ГР-2 Виконати завдання
1. Подайте у вигляді добутку вираз y p 7 8 p7.
2. Знайдіть значення функції y 4 2x , якщо значення аргументу дорівнює 3.
3. Укажіть вираз, який тотожно дорівнює виразу c a2 2.
4. Запишіть у стандартному вигляді одночлен 2a b3 4 3a b2 32.
5. Укажіть кількість коренів рівняння x 30 2 28 x .
6. Обчисліть значення виразу 52 22 33 .
ГР-3 Потрібно проаналізувати вихідні дані та певну вимогу до завдання, розв’язати одержану задачу та записати її розв’язання з поясненням чи обґрунтуванням
Сім'я Іваненко планує поїздку на море. Вони вирішили орендувати автомобіль та відправитися в подорож. 1. Витрати на паливо: Автомобіль споживає 8 літрів пального на 100 км. Подорож до моря складає 400 км. Яка загальна кількість пального знадобиться для поїздки в одну сторону?
2. Вартість пального: Вартість одного літра пального становить 36 гривень. Скільки грошей сім’я витратить на паливо для подорожі в обидва боки?
3. Кількість людей у машині: У сім'ї Іваненко є 4 особи. Якщо вони хочуть взяти ще одного друга в подорож, якою буде загальна кількість людей у машині?
про публікацію авторської розробки
Додати розробку