Дидактичні матеріали для уроків-практикумів та узагальнюючих уроків з геометрії в 7 класі

Одна з найважливіших задач школи полягає в тому, щоб прищепити учням уміння самостійно поповнювати знання, орієнтуватися в стрімкому потоці наукової, політичної й іншої інформації. Тому необхідно давати їм не просту суму знань, а їх систему.

У 7 класі розпочинається систематичне вивчення курсу геометрії. Складність даного етапу полягає в тому, що тут учні вперше зустрічаються з безліччю означень, аксіом, теорем; тут з’являються перші суворі доведення геометричних фактів. Матеріал, який вивчається в 7 класі, знаходить широке застосування у подальшому курсі геометрії. Звідси і випливає необхідність того, щоб знання з геометрії, отримані школярами в 7 класі, були глибокими, міцними і осмисленими.

Щоб сума знань учнів перетворилася на систему, на певному етапі навчання необхідна перекомпонування, систематизація матеріалу, виявлення нових зв’язків і відносин між елементами цієї суми знань. Щоб це здійснити потрібні спеціальні види роботи. Такими видами роботи можуть бути частини уроків, або цілі уроки, які називаються узагальнюючими і проводяться з метою поглиблення, систематизації та узагальнення знань. Узагальнююче повторення активізує розумову діяльність учнів, розвиває їх математичні здібності, підвищує інтерес до предмета. Все це в кінцевому результаті веде до створення системи знань з геометрії.

Але, крім узагальнення матеріалу, необхідним є і проведення уроків, які допомагають розвивати й інтелектуальні можливості. Саме такими є уроки-практикуми. Це уроки розв’язування задач із кількох логічно пов’язаних тем. Основний час у ньому відведено на кероване самостійне розв’язування задач. Цю форму використовують після вивчення великих розділів навчального курсу або в кінці навчального року.

Ціль уроків-практикумів полягає в тому, щоб виробити в учнів вміння і навички до розв’язування задач різного типу.

Посібник містить: задачі для уроків-практикумів та узагальнюючих уроків; розв’язання з пропусками; підказки-малюнки; задачі на встановлення відповідності; задачі, де необхідно вказати правильну відповідь, доповнити речення, закінчити записи.

РОЗДІЛ 1 УРОКИ – ПРАКТИКУМИ

Тема 1 Найпростіші геометричні фігури і їх властивості

Завдання 1. Накресліть відрізок завдовжки 6 см. Візьміть на відрізку довільну точку, знайдіть довжини утворених відрізків. Як перевірити, чи правильно проведене вимірювання?

Завдання 2. Точка D належить відрізку АС. Знайдіть відстань між точками А і С, якщо АD=5,3 см; СD=4,9 см.

Завдання 3. Точка К належить відрізку МN. Довжина відрізка МК дорівнює 5,2 см, а відрізок КN на 1,1 см коротший від відрізка МК. Чому дорівнює довжина відрізка МN

Завдання 4. Точки А, В, С лежать на одній прямій. Відомо, що АВ=4,7см; АС=2,1 см; ВС=6,8 см.

Чи може точка С лежати між точками А і В?
Чи може точка В лежати між точками А і С?

Завдання 5. На відрізку МN завдовжки 12 см взято точку К. Знайдіть довжини відрізків МК і КN, якщо:

відрізок МК на 3 см довший від відрізка КN;
відрізок МК у 3 рази довший від відрізка КN.

Завдання 6. На прямій АВ відмітьте точку С так, щоб точка В лежала між точками А і С. Назвіть утворені відрізки, промені. Що можна сказати про промені АВ і АС, ВА і ВС?

Завдання 7. На прямій а відмічена точка В. Відкладіть від точки В на прямій а відрізок довжиною 3,5 см. Скільки можна відкласти таких відрізків?

Завдання 8. Накресліть кут 110°. Проведіть промінь між сторонами цього кута. Виміряйте утворені кути. Як ви переконаєтесь, що вимірювання виконане правильно?

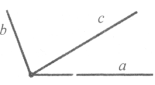
Завдання 9. Накресліть кут (аb), що дорівнює 35°. Відкладіть від променя а кут у 2 рази більший від кута (аb). Скільки можна відкласти таких кутів?

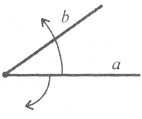
Завдання 10. Промінь с проходить між сторонами кута (аb), <(ас)=42°, а <(сb) на 13°менший від кута (ас). Чому дорівнює кут (аb)?

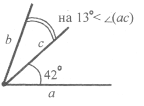
Завдання 11. Між сторонами кута (аb), що дорівнює 84°, проходить промінь с. Знайдіть кути (ас) і (сb), якщо:

кут (ас) у три рази більший від кута (сb),
кут (сb) на 6° менший від кута (ас).

Завдання 12. Чи можуть точки А, В, С лежати на одній прямій, якщо АВ=1,8 м, АС=1,3 м, ВС=3 м? Поясніть відповідь.

Завдання 13. Чи можуть три точки А, В, С лежати на одній прямій, якщо довжина найбільшого відрізка АВ менша за суму довжин відрізків АС і ВС? Поясніть відповідь.

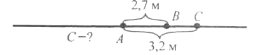
Завдання 14. Точки А, В, С лежать на одній прямій. Знайдіть довжину відрізка ВС, якщо АВ=2,7 м, АС=3,2 м. Скільки розв’язків має задача?

Завдання 15. Дано пряму і чотири точки А, В, С і D, що не лежать на цій прямій. Чи перетинає відрізок АD пряму, якщо:

відрізки АВ, ВС і СD перетинають пряму;
відрізки АС і СD перетинають пряму, а відрізок ВD не перетинає.

Завдання 16. Чи може промінь с проходити між сторонами кута (аb), якщо:

1) <(ас)=30°, <(сb)=80°, <(аb)=50°;

2) <(ас)=100°, <(сb)=90 °;

3) <(ас) більший за <(аb)?

Завдання 17. На відрізку АВ взято точку С. Знайдіть довжину відрізка АВ, якщо відрізок АС довший від відрізка ВС на 12 см, а довжини відрізків АС і ВС відносяться як 5:2.

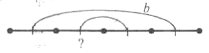
Завдання 18. 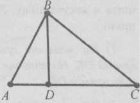Відрізок складається з чотирьох рівних частин. Відстань між серединами крайніх частин дорівнює b. Знайдіть відстань між серединами середніх частин.

Завдання 19. Відстань між точками А і В дорівнює 5 см. Знайдіть на прямій АВ такі точки, для кожної з яких сума відстаней до точок А і В дорівнює 9 см.

Завдання 20. В одному ряду фруктового саду через кожні 7,8 м посаджені яблуні, всього 27 яблунь; між кожними двома сусідніми яблунями посаджено кущ смородини. Визначити відстань від крайнього в ряді куща смородини:

до крайніх у цьому ряді яблунь;
до середньої яблуні;
до другого від краю куща смородини;
до двох середніх кущів смородини.

Тема 2 Взаємне розташування прямих на площині

Завдання 1 Дано кут АОВ. Проведемо промінь ОВ₁, доповняльний до променя ОВ. Отримаємо кут АОВ₁ суміжний із заданим. Промінь ОА – спільна сторона суміжних кутів.

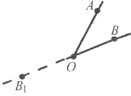
1) Намалюйте у зошитах кут АОВ. Побудуйте кут, суміжний з ним так, щоб промінь ОВ був їх спільною стороною.

2) Знайдіть кут АОВ, якщо суміжний з ним кут АОВ₁=110°.

3) Знайдіть суміжні кути, якщо один з них на 50° більший від іншого.

Завдання 2. Знайдіть суміжні кути, якщо один з них на 70° менший від іншого. Розв’яжіть задачу і вкажіть серед заданих правильну відповідь.

а) 130°; 50°; б) 125°; 55°; в) 140°; 40°; г) 110°; 70°.

Завдання 3. Знайдіть суміжні кути, якщо один з них у три рази більший від іншого.

Завдання 4. Прямі АВ і С D перетинаються у точці О.

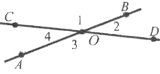
а) Дайте назву парам таки кутів:

<АОС і <СОВ; <COB і <BOD, <BOD і <DOA, <AOC і <BOD, <AOD і <COB.

б) Закінчіть записи:

<l+<2= …….. Чому?

<2+<3= ….. ?

<l ? <3

<2 ? <4

Завдання 5. При перетині двох прямих утворились кути, один з яких на 20° менший від іншого. Знайдіть усі кути.

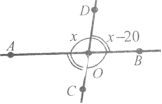
Завдання 6. При перетині двох прямих утворились кути, один з яких у 5 разів більший від другого. Знайдіть всі кути.

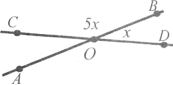
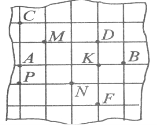
Завдання 7. Намальовано клаптик, вирваний із зошита у клітинку. Лінії на аркуші – це прямі.

а) Назвіть прямі, перпендикулярні до прямої АВ;

б) Назвіть прямі, перпендикулярні до прямої АС.

в) Відрізок DК – перпендикуляр, проведений до прямої АВ. Назвіть декілька перпендикулярів до прямої DF.

Завдання 8. Чому дорівнює кут між бісектрисою і стороною даного кута, який дорівнює: 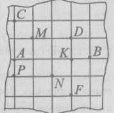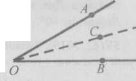1) 30°; 2) 52°; 3) 172°?

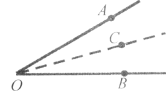
Завдання 9. Бісектриса ОD кута СОВ утворює з його стороною ОВ кут 25° Знайдіть величину кута, суміжного з кутом СОВ.

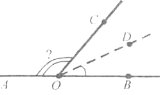
Завдання 10. Розгляньте рисунок. Назвіть точки, які є вершинами суміжних кутів. Яка точка є вершиною вертикальних кутів?

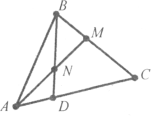
Завдання 11. Знайдіть суміжні кути, якщо їх градусні міри відносяться як: 1) 2:3; 2) 3:7; 3) 11:25; 4) 22:23.

Завдання 12. Чому дорівнює кут, якщо два суміжні з ним кути становлять у сумі 100°?

Завдання 13. Знайдіть кути, які утворюються в результаті перетину двох прямих, якщо сума трьох з них дорівнює 270°.

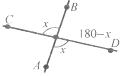
Завдання 14. Знайдіть кут між бісектрисами суміжних кутів.

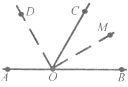
Завдання 15. З вершини О суміжних кутів АОВ і ВОС проведено промінь ОD у півплощину, де проходить спільна сторона кутів ОВ. Доведіть, що промінь ОD перетинає або відрізок АВ, або відрізок ВС. Який з відрізків перетинає промінь ОD, якщо кут АОD менший (більший) від кута АОВ? Поясніть відповідь.

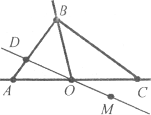
Завдання 16. З вершини розгорнутого кута (аа₁) в одну півплощину проведено промені b і с. Чому дорівнює кут (bс), якщо:

а) <(аb)=50°, <(ac)=70°;

б) <(а₁b)=50°, <(ас)=70°;

в) <(аb)=60°, <(а₁с)=30°?

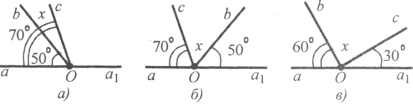
Завдання 17. Знайдіть суміжні кути, якщо бісектриса одного з них утворює з їх спільною стороною кут в 2 рази більший, ніж другий суміжний кут.

Завдання 18. Від пів прямої АВ у різних півплощинах відкладено кути ВАС і ВАD. Знайдіть кут САD, якщо:

1) <BAC=80⁰, <BAD=170⁰;

2) <BAC=87⁰, <BAD=98⁰;

3) <BAC=14⁰, <BAD=30⁰;

4) <BAC=60⁰, <BAD=70⁰.

Завдання 19. Дано <АВС=70°. Побудуйте кут BAD, що дорівнює куту ABC, так, щоб точки D і С лежали в різних півплощинах відносно прямої АВ. Чи будуть прямі ВС і AD паралельні? Відповідь обґрунтуйте.

Завдання 20. При перетині прямих АВ і CD січною PF утворились кути, величини яких записані на рисунках (а)-(д). Чи будить прямі АВ і CD паралельні в кожному з випадків?

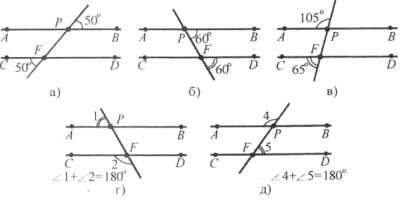
Завдання 21. Сума двох внутрішніх різносторонніх кутів при перетині двох паралельних прямих січною дорівнює 250°. Знайдіть ці кути.

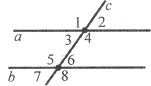
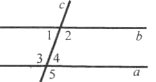
Завдання 22. При перетині паралельних прямих а і b січною с утворились кути 1-8.

а) Знайдіть <6, якщо <2=50°;

б) Знайдіть <1, якщо <8=115°;

в) Знайдіть кути 2 і 8, якщо <3=35°;

г) Знайдіть кути 4 і 5, якщо <7=82°.

Завдання 23. При перетині двох паралельних прямих січною один з внутрішніх односторонніх кутів на 20° менший від іншого. Знайдіть ці кути.

Завдання 24. Доведіть, що коли дві прямі перетинаються, то будь-яка третя пряма перетинає принаймні одну з цих прямих.

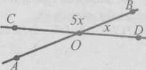
Завдання 25. Розгляньте рисунок. Знайдіть градусну міру кута х. Відповідь обґрунтуйте.

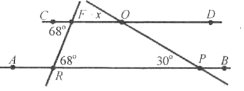
Завдання 27. На одній прямій відмічені точки М і N, а на другій – точка К так, що МN=МК, <1=<2. Доведіть, що прямі MN і KP паралельні.

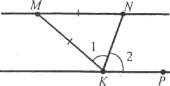
Завдання 28. При перетині двох прямих січною утворились кути такі, що <1+<5=180°, <2=110°. Знайдіть кути 1, 3, 4.

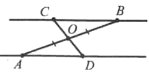
Завдання 29. Прямі СВ і АD паралельні. Відрізки АВ і СD перетинаються в точці О так, що АО=ОВ. Доведіть, що відрізки СВ і АD рівні.

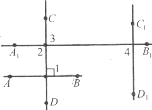
Завдання 30. Доведіть, що прямі, паралельні перпендикулярним прямим, перпендикулярні.

Тема 3 Трикутники

Завдання 1. . Розгляньте рисунок.

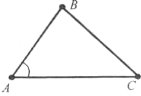
а) назвіть будь-які дві вершини трикутника АВС;

б) назвіть сторони трикутника АВС;

в) запишіть кути цього трикутника.

Завдання 2. Розгляньте рисунок.

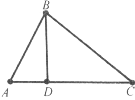
а) запишіть трикутники, що мають спільну сторону АВ;

б) вкажіть правильні рівності:

<BAC=<ВАD;
АD+DС= АС;
АВ+ВС=АС;
<АВD+<BDC=<АВС.

Завдання 3. Накресліть довільний трикутник, виміряйте його сторони і знайдіть периметр трикутника.

Завдання 4. Накресліть довільний трикутник, виміряйте його кути і знайдіть суму кутів трикутника.

Завдання 5. Трикутники АВС і МNР рівні. Знайдіть сторони трикутника МNР, якщо АВ=3 см, АС=5 см, ВС=7 см.

Завдання 6. Трикутники АВС і МNК рівні. Знайдіть кути трикутника АВС, якщо кути трикутника МNК такі: <M=40°, <N=80°, <K=60°.

Завдання 7. Трикутник АВС дорівнює трикутнику МNР. Відомо, що <A=50°, <N=60°, <P=70°, МN=6 см, АС=12 см, NР=8 см. Знайдіть невідомі кути і сторони трикутників.

Вказівка. Куту А трикутника АВС відповідає кут М трикутника МNР. Стороні МN трикутника МNР відповідає сторона АВ трикутника АВС.

Завдання 8. На малюнку зображені рівні трикутники. Відповідно рівні елементи позначені однаковими рисочками. Запишіть рівність відповідних сторін і кутів цих трикутників.

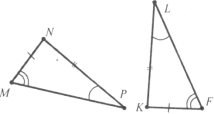
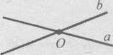
Завдання 9. Намальовано аркуш, вирваний із зошита в косу лінійку. Лінії в зошиті – це прямі.

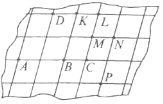
1) На малюнку пряма ВС паралельна прямій DК. Назвіть ще одну пряму, паралельну прямій ОК.

2) Чи правильні записи:

а) МN||AС;

б) АD||ВК;

в) LC||NP;

г) DK||LP?

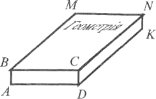
Завдання 10. На малюнку зображено підручник з геометрії. Буквами позначені його кути. Можна вважати, що деякі краї книжки паралельні між собою. Назвіть прямі, паралельні до прямої СN. Чи будуть прямі АD і ВС, СD і NК паралельними?

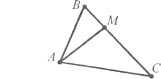
Завдання 11. Розгляньте малюнок. Запишіть три трикутники, однією з вершин яких є точка А. Вкажіть відрізки, які є одночасно сторонами двох трикутників.

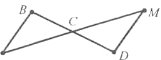
Завдання 12. На малюнку зображено два рівні трикутники. Запишіть рівності для відповідних сторін і кутів цих трикутників.

Завдання 13. Накресліть на око два рівні трикутники. Перевірте правильність побудови, вимірюючи відповідні кути і сторони.

Завдання 14. Трикутники АВС, РQR і ХУZ рівні. Відомо, що АВ=5 см, QR=6 см, XZ=7 см. Знайдіть решту сторін кожного трикутника.

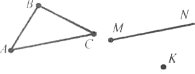
Завдання 15. Накресліть на око трикутник, рівний трикутнику АВС, що визначається променем МN та точкою К.

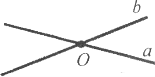
Завдання 16. Дано дві прямі, що перетинаються. Чи можна провести третю пряму, паралельну кожній із двох даних?

Завдання 17. Дано чотири прямі а, b, с і d. Відомо, що прямі а, b, с перетинаються в одній точці й прямі b, с, d також перетинаються в одній точці Доведіть, що всі чотири прямі проходять через одну точку.

Завдання 18. Дано чотири точки А, В, С. D. Відомо, що точки А, В, С лежать на одній прямій, точки В, С, D також лежать на одній прямій. Доведіть, що всі чотири точки лежать на одній прямій.

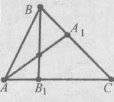
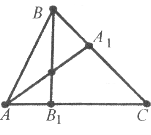
Завдання 19. Дано трикутник АВС. На стороні АС взято точку В₁, а на стороні ВС – точку А₁. Доведіть, що відрізки АА₁ і ВВ₁ перетинаються.

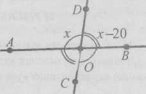
Завдання 20. На прямій розміщено послідовно п’ять точок М₁, М₂, М₃, М₄, М₅. Від якої з цих точок сума відстаней до всіх інших точок буде найменшою?

Завдання 21. Доведіть, що ∆АВС=∆ABD.

Завдання 22.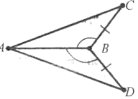
Знайдіть довжину відрізка СD. Відповідь обґрунтуйте.

Завдання 23.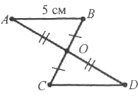
Відрізки АВ і СD перетинаються в точці О так, що СО=ОВ, <АСО=<DВО. Доведіть, що ∆АОС=∆DОВ.

Завдання 24.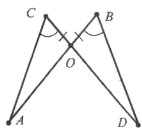
На рисунку <1=<2, АО=ОD. Доведіть, що ∆АВО=∆DСО.

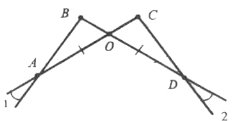
Завдання 25. Розгляньте рисунок. Однаковою кількістю дужок позначено рівні кути. Знайдіть довжину відрізка АВ, якщо ВD=8,5 см. Відповідь обґрунтуйте.

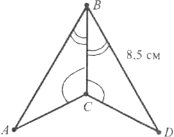
Завдання 26. Відрізки АВ=8 см і СD=14 см перетинаються в точці О і діляться нею пополам. Знайдіть периметр трикутника АОС, якщо ВD=5 см.

Завдання 27.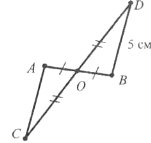
Розгляньте рисунок. Що можна сказати про трикутник АВС, якщо <1=<2? Відповідь обґрунтуйте. Назвіть його основу, бічні сторони.

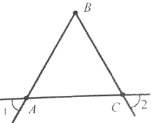
Завдання 28. Розгляньте рисунок. Чи буде трикутник АВС рівнобедреним?

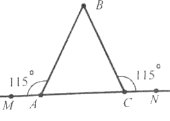
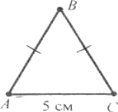
Завдання 29. Периметр рівнобедреного трикутника дорівнює 17 см. а основа 5 см. Знайдіть довжину бічної сторони.

Завдання 30. Периметр рівнобедреного трикутника дорівнюі 28 см, а бічна сторона – 9 см. Знайдіть основу трикутника.

Завдання 31. Периметр рівнобедреного трикутника дорівнює 49 см. Знайдіть його сторони, якщо бічна сторона в 3 рази більша від основи.

Завдання 32. На стороні АВ ∆АВС взято точку D, а на стороні А₁В₁ ∆А₁В₁С₁ – точку D₁. Відомо, що ∆АDС і ∆А₁D₁С₁ рівні й відрізки DВ й D₁В₁ рівні. Доведіть рівність ∆АВС і ∆А₁В₁С₁.

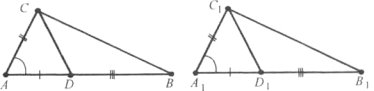
Завдання 33. Доведіть, що ∆АОВ=∆DОС, якщо АО=ОD, <1=<2.

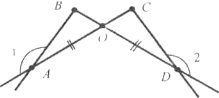
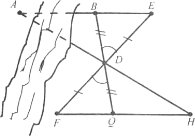
Завдання 34. Щоб виміряти на місцевості відстань між двома точками А і В, з яких одна (точка А) неприступна, провішують напрям відрізка АВ та на його продовженні відкладають довільний відрізок ВЕ. Вибирають на місцевості точку D з якої видно точку А і можна пройти до точок В і Е. Провішують прямі BDQ і ЕDF і вимірюють FD=DЕ і DQ=ВD. Далі йдуть уздовж прямої FQ, дивлячись на точку А, поки не знайдуть таку точку Н, яка лежить на прямій АD. Тоді HQ дорівнює шуканій відстані. Доведіть це.

Завдання 35. Точки А, В, С, D лежать на одній прямій. Доведіть, що коли трикутники АВЕ₁ і АВЕ₂ рівні, то трикутники СDЕ₁ і СDЕ₂ також рівні.

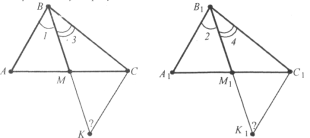
Завдання 36.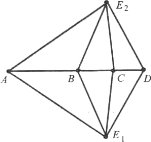
Доведіть рівність трикутників за медіаною і кутами, на які вона розбиває кут трикутника.

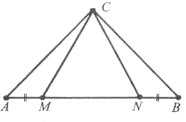
Завдання 37. Дано трикутник АВС, у якого АС=СВ. На стороні АВ взято точки М і N так, що АМ=NВ. Доведіть, що трикутник МСN – рівнобедрений.

Завдання 38. Дано: АВ=ВD, ВК=ВС. Доведіть, що ∆АКО=∆DСО.

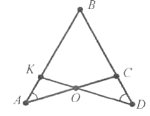
Завдання 39. Периметр рівнобедреного трикутника дорівнює 84 см, а основа відноситься до бічної сторони як 5:8. Знайдіть сторони трикутника.

Завдання 40. Розгляньте рисунок. Знайдіть кут х у кожному з випадків.

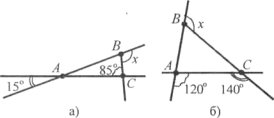
Тема 4 Прямокутний трикутник

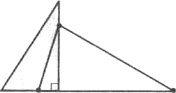
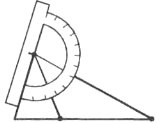
Завдання 1. Накресліть гострокутний трикутник. Користуючись лінійкою з поділками, транспортиром і косинцем, проведіть з однієї вершини медіану, бісектрису і висоту.

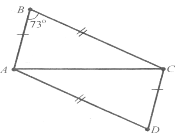
Завдання 2. Вершини В і D трикутників АВС і АDС лежать у різних півплощинах відносно прямої АС, причому АВ=СD, ВС=АD, <В=73° Знайдіть кут D.

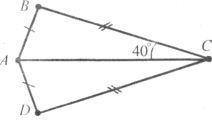
Завдання 3. Вершини В і D трикутників АВС і АDС лежать у різних півплощинах відносно прямої АС. Знаючи, що АВ=АD, ВС=DС, <ВСА=40°, знайдіть кут DСА.

Завдання 4. Користуючись лінійкою з поділками, проведіть бісектрису кута А трикутника АВС, у якого АВ=АС.

Завдання 5. Якщо бічна сторона і основа одного рівнобедреного трикутника дорівнюють бічній стороні й основі другого рівнобедреного трикутника, то трикутники рівні. Доведіть.

Завдання 6. Доведіть, що в рівнобедреному трикутнику:

а) бісектриси, проведені з вершин при основі, рівні,

б) медіани, проведені з тих самих вершин, також рівні.

Завдання 7. Вершини С і D трикутників ABC і ABD лежать по різні боки від прямої АВ. У цих трикутниках АС=AD, ВС=BD. Точка М належить променю АВ і лежить поза відрізком АВ. Доведіть рівність трикутників СВМ і DBM.

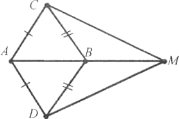
Завдання 8. Доведіть рівність рівнобедрених трикутників за бічною стороною і медіаною, проведеною до неї.

Завдання 9. Доведіть, що у рівнобедреному трикутнику висота, опущена на основу, є медіаною і бісектрисою.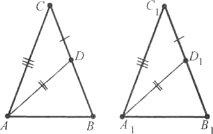

Завдання 10. Доведіть, що трикутник АВС рівнобедрений, якщо в нього:

1) медіана ВD є висотою;

2) бісектриса ВD є медіаною;

3) висота ВD є бісектрисою.

Завдання 11. Якщо основа і бісектриса, проведена до основи, одного рівнобедреного трикутника відповідно дорівнюють основі і бісектрисі, проведеній до неї, другого рівнобедреного трикутника, то такі трикутники рівні. Доведіть.

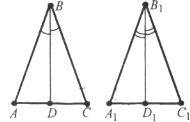
Завдання 12. Трикутники ABC і ADC рівні, причому точки В і D лежать по різні боки від прямої АС. Доведіть, що АС – бісектриса кута BAD.

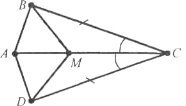
Завдання 13. Трикутники ABC і ADC рівні, причому точки В і D лежать по різні боки від прямої АС. Точка М належить стороні АС. Доведіть рівність трикутників ВСМ і DCM.

Завдання 14. Трикутники MNK і MNP рівнобедрені зі спільною основою MN, причому точки К і Р лежать по різні боки від прямої MN. Доведіть рівність трикутників МКР і NKP.

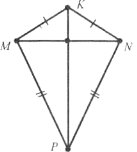
Завдання 15. Периметр рівнобедреного трикутника дорівнює 9,9 см, а бічна сторона більша від основи на 1,2 см. Знайдіть його сторони.

Завдання 16. Периметр рівнобедреного трикутника дорівнює 36,9 см, а бічна сторона більша від основи в 4 рази. Знайдіть його сторони.

Завдання 17. На бічних сторонах рівнобедреного трикутника АВС з основою АВ відкладені рівні відрізки АМ і ВN. Доведіть рівність трикутників АВN і ВАМ.

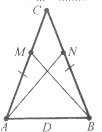
Завдання 18. Трикутники АВС і ABC₁ зі спільною основою АВ рівнобедрені. Доведіть рівність трикутників АСС₁ і ВСС₁.

Завдання 19. Відрізки АВ і СD однакової довжини перетинаються в точці О так, що АО=ОD. Доведіть рівність трикутників АВС і DСВ.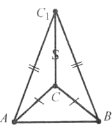

Завдання 20. Доведіть рівність рівнобедрених трикутників за бічною стороною і висотою, опущеною на бічну сторону.

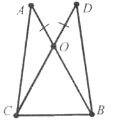
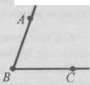
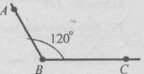
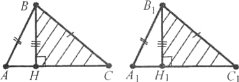
Завдання 21. Доведіть рівність рівнобедрених трикутників за основою і висотою, опущеною на бічну сторону.

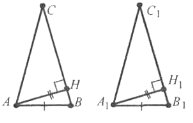
Завдання 22. Доведіть рівність трикутників за стороною, прилеглим до неї кутом і бісектрисою цього кута.

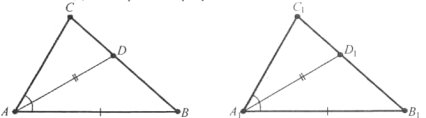
Завдання 23. Доведіть рівність трикутників за двома сторонами і висотою, проведеною до третьої сторони.

Тема 5 Коло і круг

Завдання 1. Накресліть коло, діаметр якого дорівнює 6 см. Проведіть та позначте радіус кола, діаметр, хорду і дотичну.

Завдання 2. Візьміть на колі довільну точку. Скільки діаметрів, хорд, дотичних можна провести через цю точку? Чи можна провести хорду в 2 рази більшу від радіуса, у 3 рази більшу?

Завдання 3. Накресліть коло, радіус якого дорівнює 2,5 см. Проведіть довільну хорду АВ, знайдіть її середину – точку С. Як розміщені прямі АВ і ОС? (О – центр кола). Чому?

Завдання 4. У коло, радіус якого дорівнює 3,5 см, впишіть трикутник, одна сторона якого проходить через центр кола. Яка довжина цієї сторони?

Завдання 5. Навколо кола радіуса 1,5 см опишіть трикутник, одна сторона якого дорівнює 4 см.

Завдання 6.У трикутник АВС вписано коло з центром О. Знайдіть кут АОВ, якщо <A=56°, <В=48°.

Завдання 7. Через точку кола проведені діцметр, хорда та дотична. Кут між діаметром і хордою дорівнює 38°. Чому дорівнює менший з кутів між хордою і дотичною?

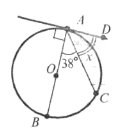
Завдання 8. Дано коло з центром О, АВ – хорда, АВ=ОА, AN – дотична. Знайдіть <ВАN.

Завдання 9. Кола, радіуси яких дорівнюють 4,2 см і 2,3 см, мають зовнішній дотик. Чому дорівнює відстань між центрами кіл?

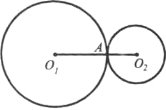
Завдання 10. Кола, радіуси яких дорівнюють 3,6 см і 2,8 см, мають внутрішній дотик. Чому дорівнює відстань між центрами кіл?

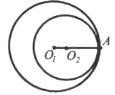
Завдання 11. Кут між діаметром АВ і хордою АС дорівнює 80°. Знайдіть кути трикутника АВС.

Завдання 12. Трикутник АВС вписаний у коло з центром у точці О. Чому дорівнює кут В, Якщо <АОВ=140°, <ВОС=110°?

Завдання 13. З точки кола А проведені хорда АВ та дотична AN. Знайдіть гострий кут між хордою та дотичною, якщо:

1) <АОВ=110°;

2) <АОВ=α (О – центр кола).

Завдання 14. У трикутнику АВС центр описаного кола лежить на медіані АО. Що можна сказати про цей трикутник?

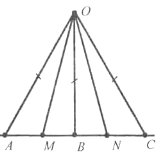
Завдання 15. 1) Точки А, В, С лежать на прямій, а точка О – поза прямою. Чи можуть два трикутники АОВ і ВОС бути рівнобедреними з основами АВ і ВС? Поясніть відповідь.

2) Чи можуть коло і пряма перетинатися більше, ніжу двох точках?

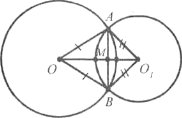
Завдання 16. 1) Кола з центрами О і О₁ перетинаються в точках А і В. Доведіть, що пряма АВ перпендикулярна до прямої ОО₁.

2)Доведіть, що два кола не можуть перетинатися більше, ніжу двох точках.

Завдання 17. 1) З однієї точки до кола проведено дві дотичні. Доведіть, що відрізки дотичних МР і MQ рівні.

2). Доведіть, що через одну точку не може проходити більше двох дотичних до кола.

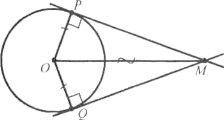
Завдання 18. Одне коло описане навколо рівностороннього трикутника, а друге – вписане в нього. Доведіть, що центри цих кіл збігаються.

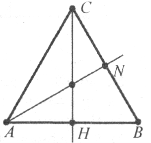
Завдання 19. Коло, вписане у трикутник АВС, дотикається до його сторін у точках А₁, В₁, С₁ .Доведіть, що АС₁=0,5(АВ+АС-ВС).

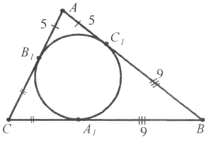
Завдання 20. Коло, вписане у трикутник АВС, дотикається до його сторін у точках А₁, В₁, С₁. Периметр трикутника АВС дорівнює 50 см, АС₁=5см, ВС₁=9 см. Знайдіть сторони трикутника АВС.

РОЗДІЛ 2 УЗАГАЛЬНЮЮЧІ УРОКИ

Тема 1 Найпростіші геометричні фігури і їх властивості

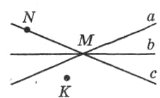
Завдання 1. Користуючись рисунком, продовжити речення:

а) точка М належить прямим …;

б) точка N належить …;

в) точка N не належить …;

г) точка К не належить ….

Завдання 2. Накреслити пряму т. Позначити точку А, яка належить прямій т, і точку В, яка не належить цій прямій. Провести пряму АВ.

а) Яке взаємне розміщення прямих т і АВ?

б) Чи завжди через точки А і В можна провести пряму? Пояснити.

в) Скільки прямих можна провести через точки А і В? Чому?

Завдання 3. Відмітити знаком «+» ті запитання, відповіді на які ти знаєш, знаком «-» ті, на які не знаєш.

а) Що називається відрізком?

б) Які основні властивості розміщення точок на прямій і на площині?

в) Що називається променем, або півпрямою?

г) Які основні властивості вимірювання відрізків?

ґ) Яка геометрична фігура називається кутом?

Назвати елементи кута.

д) Які основні властивості вимірювання кутів?

е) Що називається бісектрисою кута?

є) Який кут називається розгорнутим?

Завдання 4. З’єднати кожен запис із відповідним йому рисунком.

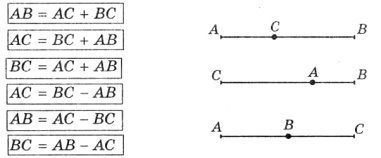
Завдання 5. З поданих умов вибрати ту, яка відповідає даному рисунку:

а) Дано: К є МР, б) Дано: К є МР, в) Дано: К є МР,

МР=7 см, МК=10 см, МР=10 см,

КР=10 см МР=7 см. КР=7 см.

Знайти: МК Знайти: КР Знайти: МК

Завдання 6. На прямій від точки А відкладені відрізки АВ=6см і АС=15см. Знайти довжину відрізка ВС. Скільки розв’язків має задача?

Завдання 7. Точка D належить відрізку РМ, довжина якого 28 см. Знайти відрізки FD і МD, якщо їх довжини відносяться як 3:4.

Завдання 8. Визначити, якого виду є кожний з кутів.

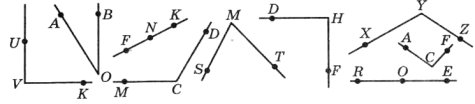
Завдання 9. Виміряти і записати градусні міри кутів, зображених на рисунках.

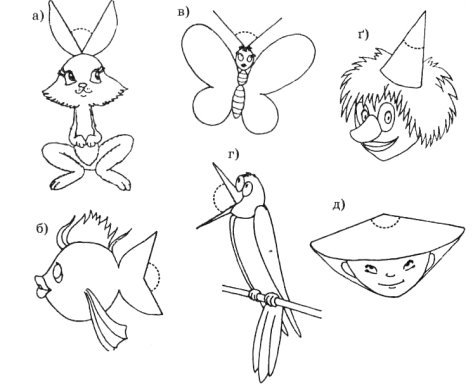
Завдання 10. У кожному із завдань підкреслити правильну відповідь.

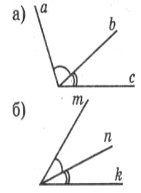а) Якщо <(ac)=120°, <(bc)=40°, то:

1) <(ab)=160°;

2) <(ab)=60°;

3) <(ab)=80°.

б) Якщо <(mk)=60°, <(mn)=38°, то:

1) <(nk)=22°;

2) <(nk)=98°;

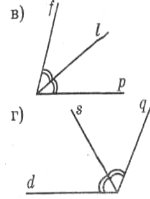3) <(nk)=30°.

в) Якщо <(fp)=80°, і l – бісектриса, то:

1) <(lp)=160°;

2) <(lp)=40°;

3) <(fl)=40°.

г) Якщо s – бісектриса <(dq), <(ds)=50°, то:

1) <(dq)=100°;

2) <(dq)=50°;

3) <(sq)=100°.

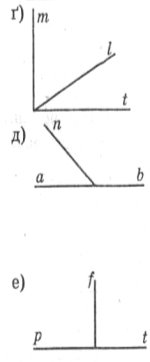
г) Якщо <(mt) – прямий, <(lt) становить від <(mt), то:

1) <(lt)=30°;

2) <(ml)=60°;

3) <(ml)=30°.

д) Якщо <(ab) – розгорнутий, < (an) становить 0,25 від <(ab), то:

1) <(an)=90°;

2) <(an)=40°;

3) <(an)=45°.

е) Якщо <(fp) – прямий, f – бісектриса <(pt), то:

1) <(pt)=160°;

2) <(pt)=180°;

3) <(pt) – розгорнутий.

Завдання 11. Знайти величини кутів, що утворились при перетині поямих т і п, якщо сума трьох з них дорівнює 290°.

Завдання 12. Розв’язати задачу. Відрізок, довжина якого 50 см, розділено на три нерівні відрізки. Відстань між серединами крайніх з них дорівнює 28 см. Знайти довжину середнього з них.

Тема 2 Взаємне розташування прямих на площині

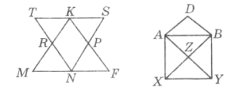
Завдання 1. Користуючись рисунком, вставити пропущене:

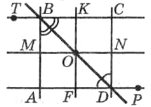
а) промені DP і …… є доповняльними;

б) <TBD і ……, <MOK і …… є суміжними;

в) <ВОК і ……, <МОF і …… є вертикальними;

г) прямі СТ і ….. , КР і ….. паралельні, тобто СТ || ….. ,КР ||……;

ґ) прямі МН і ….., КР і ….. перпендикулярні, тобто МН┴ ….., КР┴……;

д) ВО – бісектриса кута …..; DO – бісектриса кута …...

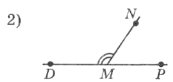
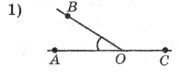Задання 2. Користуючись рисунками, вибрати правильну відповідь:

<AOB=30°, тоді <BOC: <DMN=120°, тоді <NMP:

а) 30°; б) 150°; в) 180°; а) 120°; б) 90°; в) 60°;

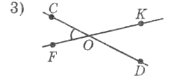
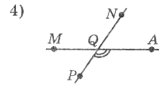
<COP=40°, тоді <KOD: <AQP=135°, тоді <MQN:

а) 40°; б) 140°; в) 50°; а) 150°; б) 180°; в) 135°.

Завдання 3. Показати на рисунках, як розташовані стрілки годинника у вказаний час. Записати градусні міри кутів, які вони утворюють, та градусні міри кутів, суміжних з утвореними.

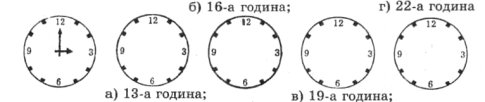
Завдання 4. Розв’язати задачі:

а) Один із суміжних кутів більший за іншого у 8 разів. Знайти ці кути.

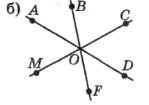б) Дано: AD, BF, CM – прямі, О – точка перетину, <АОВ=50⁰, <MOF=70⁰. <AOC, <BOD, <COF, <COD.

Завдання 5. Дайте відповіді на запитання:

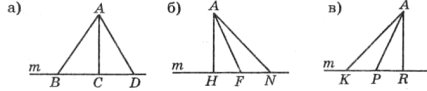
1) Який з відрізків є перпендикуляром, проведеним з точки А до прямої т?

2) Чому дорівнює відстань від точки В до прямої n?

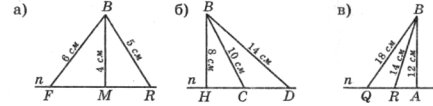
Завдання 6. На кожному з рисунків кути, утворені при перетині двох прямих січною, позначити цифрами 1, 2, З, 4, 5, 6, 7, 8 так, щоб дані твердження були правильними.

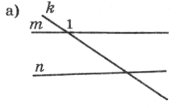
<l і <2, <5 і <6 – суміжні;

<3, <5 і <7 – вертикальні;

<3 і <6, <4 і <5 – внутрішні різносторонні;

<3 і <5, <4 і <6 – внутрішні односторонні;

<l і <6, <2 і <5, <3 і <8, <4 і <7 – відповідні.

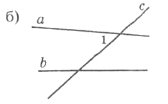
<l і <4, <2 і <3 – суміжні;

<2 і <8, < 4 і <6 – вертикальні;

<1 і <3, <2 і <4 – внутрішні різносторонні;

<1 і <2, <3 і <4 – внутрішні односторонні;

<l і <7, <2 і <6, <3 і <5, <4 і <8 – відповідні.

Завдання 7. Визначте пари паралельних прямих, якщо:

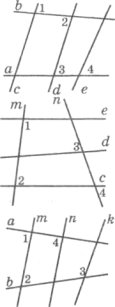
а) <1=<2, <3≠<4.

б) <1+<2=180⁰, <3 > <4.

в) <1=<4, <2+<3≠180⁰.

Завдання 8. Знайти градусну міру кутів: <DAB, <ABC, <BCD, <CDA, якщо <ABF=32⁰, AD||BC, AB||CD.

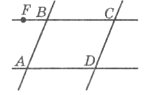
Завдання 9. З’єднайте кожне із поданих речень з відповідним йому продовженням.

Завдання 10. У кожному з тверджень вибрати необхідне слово:

а) промені, на які точка дiлить пряму, називаються /розгорнутими/ доповняльними/ прямими/;

б) два кути називаються /вертикальними/ суміжними/ розгорнутими/, якщо у них одна сторона спільна, а дві інші є доповняльними півпрямими;

в) сума суміжних кутів дорівнює /90°/ 100°/ 180°/;

г) якщо два кути рівні, то суміжні з ними кути /різні/ рівні/ гострі/;

ґ) два кути називаються /вертикальними/ суміжними/ гострими/, якщо сторони одного кута є доповняльними півпрямими сторін другого;

д) вертикальні кути / різні/ рівні/ гострі/;

е) дві прямі називаються /паралельними/ перпендикулярними/ рівними/, якщо вони не перетинаються;

є) через точку, що не лежить на даній прямій, можна провести не більше ніж /одну/ дві/ три/ прямі, паралельні даній;

ж) дві прямі називаються /паралельними/ перпендикулярними/ рівними/, якщо вони перетинаються під прямим кутом;

з) через кожну точку прямої можна провести перпендикулярну (і) до неї пряму(і), до того ж тільки /одну/ дві/ три/;

и) промінь, який виходить з вершини кута, проходить між його сторонами і ділить кут навпіл, називається /перпендикуляром/ бісектрисою/ стороною/.

Тема 3 Трикутники

Завдання 1. Знайти всі трикутники і порахувати їх на кожному з рисунків.

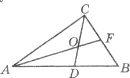
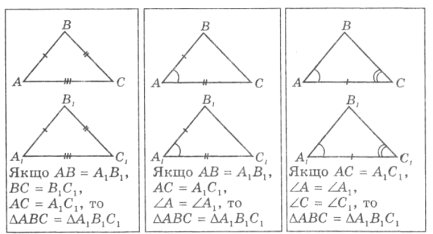
Завдання 2. З’єднати номер кожної ознаки рівності трикутників з відповідним йому рисунком.

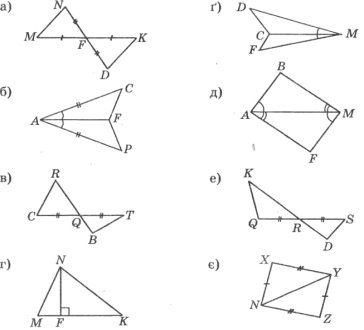
Завдання 3. Вибрати ті рисунки, на яких зображено рівні трикутники. Записати рівні трикутники.

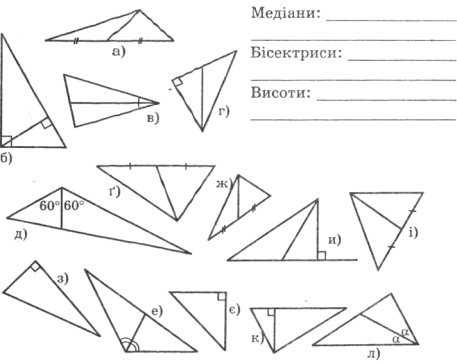
Завдання 4. Указати, в яких трикутниках проведено медіани, в яких – бісектриси, в яких – висоти.

Завдання 5. Підкреслити правильні відповіді.

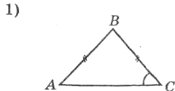
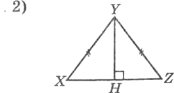
Якщо <С=50°, то <A: Якщо XY=10 см, XH=6 см, то P_∆_XYZ:

а) 90°; б) 50°; в) 130°. а) 26 см, б) 16 см, в) 32 см.

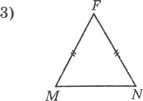
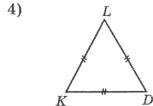
Якщо МF=4 см, МТ=5 см, то P_∆_MNF: Якщо KL=10 см, то P_∆_KLD:

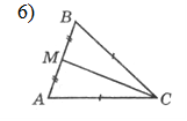
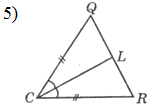
а) 14 см; б) 9 см; в) 13 см. а) 30 см; б) 10 см; в) 20 см.

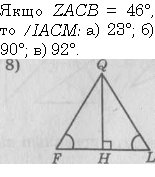
Якщо CQ=5 см, QR=6 см, Якщо <ACB=46⁰, то <ACM:

СL=4 см, то P_∆_CRL:

а) 14 см; б) 16 см; в) 12 см. а) 23⁰, б) 90⁰, в) 92⁰.

Завдання 6. У трикутнику АВС: <АВС=90°, АD=ВD=DС, D є АС, <ВАD=64°. Знайти <DСВ.

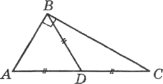
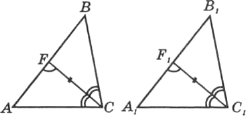
Завдання 7.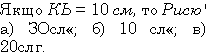
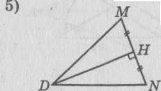
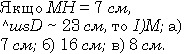
Довести рівність трикутників за кутом, бісектрисою цього кута і кутом, який утворює бісектриса з протилежною стороною.

Тема 4 Прямокутний трикутник

Завдання 1. Закреслити гострокутні і тупокутні трикутники.

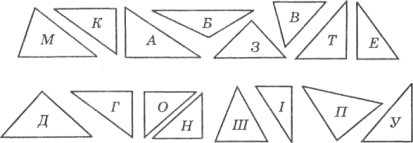
Як називаються трикутники, що залишились?

Із букв, записаних у цих трикутниках, скласти назви сторін прямокутного трикутника.

Завдання 2. Вставити пропущене:

а) сума гострих кутів прямокутного трикутника дорівнює …………;

б) катет прямокутного трикутника, який лежить проти кута 30°, дорівнює…….;

в) якщо катет прямокутного трикутника дорівнює половині гіпотенузи, то кут, який лежить проти цього катета, дорівнює………;

г) у рівнобедреному прямокутнику гострі кути дорівнюють………….;

ґ) сума кутів трикутника дорівнює………….;

д) зовнішній кут трикутника дорівнює …… внутрішніх кутів, не суміжних з ним;

е) кожна сторона трикутника ……… суми двох інших сторін.

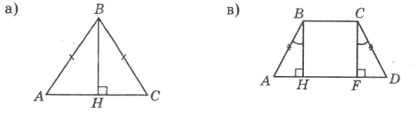
Завдання 3. Визначити і записати рівні трикутники на кожному з рисунків. Сформулювати ознаку рівності до кожної пари трикутників.

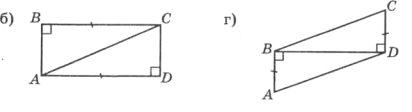
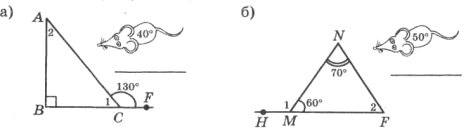
Завдання 4. У яку «нірку» заховається кожне мишеня? (Записати номер кута трикутника)

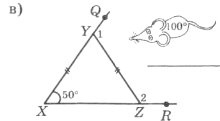
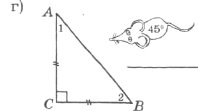
Завдання 5. Знайти градусні міри кутів трикутника, якщо вони відносяться як 1:2:6. Визначити вид трикутника.

Завдання 6. У прямокутному трикутнику АВС (<C=90°) проведена висота СD (D є АВ). Знайти довжини відрізків АD і ВD, якщо гіпотенуза дорівнює 16см, а <САВ=30°.

Завдання 7. Дано довжини відрізків АВ, ВС і АС:

а) АВ=6 см; АС=7 см, ВС=1 см;

б) АВ=4 см, АС=3 см, ВС=5 см;

в) АВ=8 см, АС=4 см, ВС=4 см;

г) АВ=9 см, АС=2 см, ВС=5 см;

ґ) АВ=10 см, АС=10 см, ВС=21 см;

д) АВ=12 см, АС=9 см, ВС=6 см.

Визначити, в якому випадку точки А, В і С:

1) є вершинами трикутника;

2) лежать на одній прямій;

3) не лежать на одній прямій і не є вершинами трикутника.

Завдання 8. Одна зі сторін трикутника дорівнює 0,5 см, а друга – 1,7 см. Знайти довжину третьої сторони, якщо відомо, що вона виражається натуральним числом.

Завдання 9. Кут між бісектрисою і висотою, проведеними з вершини найбільшого з кутів прямокутного трикутника, дорівнює 18⁰. Знайти гострі кути даного трикутника.

Завдання 10. Не відриваючи олівця від зошита і не проводячи двічі ту саму лінію, накреслити фігуру.

Тема 5 Коло і круг

Завдання 1. Вставити пропущене.

а) Коло – це геометрична фігура, яка складається з усіх точок площини, розміщених на …… від даної …..;

б) радіус кола – це відрізок, який сполучає центр кола з ….. ;

в) хорда кола – це відрізок, який сполучає дві ….. ;

г) діаметр кола – це хорда, яка проходить через …..;

ґ) діаметр кола у ….. рази більший від його радіусу;

д) круг – це геометрична фігура, яка складається з усіх точок площини, розміщених на відстані, ….. від даної точки;

е) дотична до кола – це пряма, яка має з колом ….. точку;

є) дотична до кола – ….. до радіусу, проведеного в точку дотику.

Завдання 2. Підкреслити правильні відповіді:

1) коло, вписане в трикутник, зображене на рисунку:

2) центром кола, вписаного у трикутник, є точка перетину його:

а) медіан;

б) бісектрис;

в) серединних перпендикулярів до сторін трикутника;

г) висот;

3) коло, описане навколо трикутника, зображене на рисунку:

4) центром кола, описаного навколо трикутника, є точка перетину його:

а) медіан;

б) бісектрис;

в) серединних перпендикулярів до сторін трикутника;

г) висот;

5) залежність між радіусом (r) і діаметром (d) кола виражається рівністю:

а) ;

б) ;

в) ;

г) .

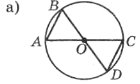
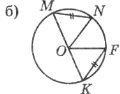
Завдання 3. Доведіть рівність трикутників.

Завдання 4. Виберіть правильну відповідь.

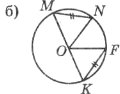
<OMN дорівнює: <OZY дорівнює:

1) 70°; 2) 35°; 3) 60°. 1) 45°; 2) 50°; 3) 25°.

<OАВ дорівнює: FT дорівнює:

1)90°; 2) 30°; 3) 45°. 1) 4 см; 2) 2 см; 3) 1 см.

<OCD дорівнює: FT дорівнює:

1) 60°; 2) 45°; 3) 90°. 1) 6 см; 2) 1,5 см; 3) 3 см.

<NOL дорівнює:

1) 45°; 2) 90°; 3) 30°.

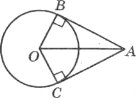
Завдання 5. Радіус кола з центром у точці О дорівнює 6 см. Точка А розміщена поза колом так, що ОА=12см. Знайти кут між дотичними, проведеними з точки А до даного кола.

Завдання 6. Пряма АВ дотикається до кола у точці F. Знайти <DFВ, якщо <DОF=120°.

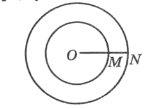
Завдання 7. Дано два концентричних кола з центром у точці О. Відомо, що МN=14см, а радіуси кіл відносяться як 5:3. Знайти радіуси кіл.

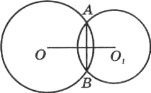
Завдання 8. Довести, що спільна хорда двох кіл, які перетинаються, перпендикулярна до відрізка, що сполучає їх центри.

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ

Адруг Л. М. Геометрія. – Харків, 2007. – 30 с.
Апостолова Г.В. Геометрія. Підручник для 7 класу загальноосвітніх навчальних закладів. – Генеза, 2015. – 216 с.
Бевз Г.П., Бевз В.Г., Владімірова Н.Г. Геометрія. Підручник для 7 класу загальноосвітніх навчальних закладів. – К.: Зодіак-ЕКО, 2007. – 207 с.
Бурда М.І., Тарасенкова Н.А. Геометрія Підручник для 7 класу загальноосвітніх навчальних закладів. – К.: Зодіак-ЕКО, 2007. – 207 с.
Істер О.С. Геометрія. Підручник для 7 класу загальноосвітніх навчальних закладів. – К.: Освіта, 2007. – 159 с.
Єршова А.П., Голобородько В.В., Крижановський А.Ф. Геометрія 7 клас. Збірник самостійних і контрольних робіт. – Х.: Ранок-Веста, 2015. – 224 с.
Єршова А.П., Голобородько В.В., Крижановський А.Ф. Геометрія. Підручник для 7 класу загальноосвітніх навчальних закладів. – Х.: Ранок, 2007. – 80 с.
Мерзляк А.Г., Полонський В.Б., Якір М.С. Геометрія Підручник для 7 класу. Для середнього шкільного віку. – Харків: «Гімназія», 2007. – 198 с.
Підручна Я.В., Янченко Г.М. Уроки з геометрії. – Тернопіль: Підручники й посібники, 2001. – 64 с.
Тадеєв В.О. Геометрія. Підручник для 7 класу загальноосвітніх навчальних закладів. – Тернопіль.: Навчальна книга – Богдан, 2015. – 296 с.

docx

Завантажити

Зберегти на потім

Додав(-ла)

Кислюк Ольга Олександрівна

Пов’язані теми

Геометрія, 7 клас, Матеріали до уроків

Додано

3 жовтня 2018

Переглядів

4059

Оцінка розробки

Відгуки відсутні