Дидактичні матеріали з математики для 5 класу

Самостійна робота № 1 з теми  «Натуральні числа»

Варіант 1

1.Записати цифрами числа:

   а) десять мільярдів вісімдесят тисяч п’ять;

   б) чотириста п’ятдесят мільйонів п’ятдесят.

2. Запишіть число, у якого:

   а) 1 сотня 2 десятки 3 одиниці;

   б) 9 сотень 7 десятків;

   в) 2 тисячі 3 сотні 1 десяток.

3. Округліть число 12 475 836:

   а) до десятків;

   б) до тисяч;

   в) мільйонів.

4. Дано три числа: 359; 4 327;804. Обчислити:

   а) суму цих чисел і округлити результат до сотень;

   б) суму округлених до сотень чисел.

5*. Запишіть усі трицифрові числа, у яких число одиниць у 2 рази більше від числа десятків, а число сотень більше від числа одиниць на 1

 

 

 

 

 

 

 

 

Самостійна робота № 1 з теми  «Натуральні числа»

Варіант 2

1.Записати цифрами числа:

   а) вісімдесят вісім мільярдів п’ятдесят три тисячі;

   б) дев’ятсот дев’яносто три мільйони двадцять.

2. Запишіть число, у якого:

   а) 8 сотень 3 десятки 4 одиниці;

   б) 4 сотні 5 одиниць;

   в) 5 тисяч 1 сотня 4 одиниці.

3. Округліть число 82 436 975:

   а) до десятків;

   б) до тисяч;

   в) мільйонів.

4. Дано три числа: 35; 789; 4 932. Обчислити:

   а) суму цих чисел і округлити результат до десятків;

   б) суму округлених до десятків  чисел.

5*. Запишіть усі трицифрові числа, у яких число сотень у 3 рази менше від числа десятків, а число одиниць менше від числа десятків на 1.

 

Самостійна робота № 2 з теми «Додавання і віднімання натуральних чисел»

Варіант 1

      1. Як називається результат дії додавання?

      2. Як називається компонент дії віднімання, який стоїть на першому місці?

      3. Виконайте дії:

   а) 32 749 + 780 664;     б) 286 325 – 96 162.   

4. Обчисліть на скільки число 59 428:

   а) більше від 54 609;

   б) менше від 79 529.

5. Обчисліть зручним способом:

   а) 274 + 1 537 + 463;

   б) 756 – (356 + 235).

6. В овочесховищі  було 313 т  картоплі. У понеділок привезли на 176 т більше, ніж було в овочесховищі, а у вівторок – на 43 т менше, ніж привезли в понеділок. Скільки тонн картоплі стало в овочесховищі?   

Самостійна робота № 2 з теми «Додавання і віднімання натуральних чисел»

Варіант 2

  1. Як називається результат дії віднімання?

  2. Як називається компонент дії віднімання, який стоїть на другому місці?

 3. Виконайте дії:

   а) 499 654 + 80 261;     б) 178 214 – 94 153.   

4. Обчисліть на скільки число 48 234:

   а) більше від 42 627;

   б) менше від 58 974.

5. Обчисліть зручним способом:

   а) 241 + 2 427 + 373;

   б) (654 + 289) – 454.

6. До будівельного майданчику привезли 340 т щебеню, що на 81 т більше, ніж піску, і на 103 т менше, ніж цементу. Скільки всього привезли будівельних матеріалів?

 

Контрольна робота № 1 за тему «Натуральні числа. Додавання і віднімання натуральних чисел.»

Варіант 1

1. Виконайте дії:

   а) 588 761 + 40 319;     б) 954 749 – 87 124.

2. Не використовуючи калькулятора, обчисліть, обираючи зручний порядок дій:

   а) (1 873 + 1 227) – 873;     б) 641 – (141 – 98);

   в) (797 + 512) – 112;           г) 5 124 + 676 + 4 876.

3. На залізничну станцію прийшов поїзд із 97 товарних вагонів. Після того, як частину вагонів відчепили, залишилося 48 вагонів. Скільки вагонів відчепили?

4*. У трьох п’ятих класах 100 учнів. У 5-А і 5-Б 65 учнів, а в 5-А і 5-В – 66. Скільки учнів у кожному класі?

Контрольна робота № 1 за тему «Натуральні числа. Додавання і віднімання натуральних чисел.»

Варіант 2

1. Виконайте дії:

   а) 724 564 + 90 737;     б) 843 524 – 29 846.

2. Не використовуючи калькулятора, обчисліть, обираючи зручний порядок дій:

   а) (7 122 + 678) – 122;  б) 993 – (693 – 108);

   в) (129 + 741) – 441; г) 1 271 + 549 + 2 729. 

3. На складі зберігалося 127 ящиків із фруктами. Після того як привезли ще партію ящиків із фруктами, на складі всього стало 173 ящики. Скільки ящиків із фруктами привезли на склад?

4*. За три дні було скошено траву на лузі площею 35 га. За перший і другий день було скошено траву на площі 22 га. А за другий і третій – на площі 25 га. Скільки гектарів лугу скошували кожного дня?               

 

 

 

Самостійна робота № 3 з теми «Величини. Вирази. Формули. Рівняння»

Варіант 1

1.Подайте:

а) 4 м 5 см  у сантиметрах;

б) 4 023 м  у кілометрах і метрах.

2. Знайдіть значення виразу 7 420 : х + 29, якщо х = 7.

3. Поїзд ішов 3 год. зі швидкістю V км/год. Який шлях пройшов поїзд? Обчисліть шлях, пройдений поїздом, якщо V = 18.

4. У залі для глядачів кінотеатру в кожному ряді р місць, а кількість рядів на 2 менша, ніж кількість місць у ряді. Скільки всього місць у залі для глядачів?

5*. Складіть вираз для розв’язування задачі.

Купили 2 коробки шоколадних цукерок і 3 коробки карамельок. У кожній коробці 20 шоколадних цукерок, а карамельок на k штук більше. Скільки цукерок в усіх коробках?

 

 

Самостійна робота № 3 з теми «Величини. Вирази. Формули. Рівняння»

 Варіант 2

1.Подайте:

а) 5 км 32 м  у метрах;

б) 702 дм  у метрах і дециметрах.

2. Знайдіть значення виразу 581 – (202 + k), якщо k = 7.

3. Який шлях пройшов поїзд за 6 год, якщо він ішов зі швидкістю т км/год? Обчисліть шлях, пройдений поїздом, якщо т = 60.

4. На ділянці посадили k рядів розсади капусти. Кількість рослин у кожному ряді на 5 більша, ніж кількість рядів. Скільки всього розсади капусти посадили на ділянці?

 5*. Складіть вираз для розв’язування задачі.

У саду зібрали 5 ящиків яблук і 3 кошики груш. У кожному ящику т кг яблук, а в кожному кошику груш на 3 кг менше, ніж яблук у ящику. Скільки всього зібрали фруктів?

 

Контрольна робота № 2 за тему «Величини. Вирази. Формули. Рівняння.»

Варіант 1

1.              Порівняйте числа, результат порівняння запишіть за допомогою знака «< » або « > »:

а) 3 000 080  і  3 000 100;      б) 75 102  і  75 201.

2. Знайдіть значення виразу 140 : а + 56, якщо а = 28.

3. Знайдіть натуральні числа, що є розв’язками нерівності 11< х <14.

4. Розв’яжіть рівняння:

а) x – 49 = 129; б) (х + 25) – 76 = 34.

5*. Автомобіль проїхав 120 км за 2 години. За скільки годин він проїде s км, якщо їхатиме з тією самою швидкістю? Складіть вираз для розв’язання задачі. Обчисліть його значення, якщо s = 600.

 

Контрольна робота № 2 за тему «Величини. Вирази. Формули. Рівняння.»

Варіант 2

1.              Порівняйте числа, результат порівняння запишіть за допомогою знака «< » або « > »:

а) 7 003 802  і  7 003 812;      б) 91 123  і  91 103.

2. Знайдіть значення виразу 180 : b + 56, якщо b = 12.

3. Знайдіть натуральні числа, що є розв’язками нерівності 10< х <13.

4. Розв’яжіть рівняння:

а) x + 29 = 43; б)(х –  49) + 51 = 71.

5*. Тракторист зорав за 3 години 60 а землі. За скільки годин цей тракторист зоре S а землі, якщо продуктивність залишиться тією самою? Складіть вираз для розв’язування задачі. Обчисліть його значення, якщо S = 120. 

 

Самостійна робота № 4 з теми «Властивості множення натуральних чисел»

Варіант 1

1. Запишіть переставний закон множення для довільних чисел х і у.
2. Запишіть розподільний закон множення : відносно дії віднімання для довільних чисел s, t, p.
3. Обчисліть, обираючи зручний порядок дій:     

а) 4  · 256  · 25;   б) 4  · 680  ·  25;   в) 8  · 100  ·  5;             

г) 34 · 7 + 34 · 93;  д) 93 · 25 + 107 · 25; е) 254 · 125 + 254 · 875

4. Спростіть вираз:         

а) 19p + 21p;  б) 41k  + 23k + k;  в) 29x + 14x – 10x.

5. Розв’яжіть рівняння:                       а) 28х + 5х = 99;                            б) (х – 2)(8 – х) = 0.

 

Самостійна робота № 4 з теми «Властивості множення натуральних чисел»

Варіант 2

1. Запишіть сполучний закон множення для довільних чисел т, п і k.
2. Запишіть розподільний закон множення відносно дії додавання для довільних чисел s, t, p.
3. Обчисліть, обираючи зручний порядок дій:    

а) 125  ·  17  ·  8;  б) 500  ·  129  ·  2;  в) 40  ·  32  ·  25;             

г) 73 · 15 – 15 · 71; д) 125 · 423 + 125 · 377; е) 441 · 16 + 559 · 16.

4. Спростіть вираз:                        а) 13х + 2х;                            б) 15у + 24у – 9у;                            в) 72b – 8b – b .
5. Розв’яжіть рівняння:                       а) 15х + 10х = 75;                            б) (х – 3)(7 – х) = 0.

 

Самостійна робота № 5  з теми «Ділення натуральних чисел»

Варіант 1

1. Знайдіть значення виразу 4 256 : 76 + 48 · 36.
2. Спростіть вираз 218х – 198х і знайдіть його значення, якщо х = 24.
3. Розв’яжіть рівняння: 5z + z – 42 = 18.
4. Знайдіть значення виразу: 156 · 49 +227 · 49 – 283 · 49.
5. Виконайте ділення з остачею:       а) 15 740 : 33 - результат округліть до десятків;                            б) 27 973 : 872 - результат округліть до сотень.

 

Самостійна робота № 5  з теми «Ділення натуральних чисел»

Варіант 2

1. Знайдіть значення виразу 2 – 3 · 19 – 4690 : 70.
2. Спростіть вираз 89х-49х і знайдіть його значення, якщо х =  16.
3. Розв’яжіть рівняння 7m + m – 42 = 38.
4. Знайдіть значення виразу: 239 · 37 – 208 · 37 + 169 · 37.
5. Виконайте ділення з остачею:       а) 78 909 : 76 - результат округліть до сотень;                                          б) 66 666 : 689 - результат округліть до десятків.

 

 

Контрольна робота № 3 за тему «Множення і ділення натуральних чисел»

Варіант 1

1. Перемножити і результат перевірити діленням: 605 · 38.
2. Виконайте дії:
   1. 512 · 625 – 126 840 : 280;
   2. 32 + (749 - 29) : 15.
3. Розв’яжіть рівняння:
   1. 531 648 : х = 526;
   2. (х - 56) · 9 = 909.
4. На одній ділянці росте 188 кущів, що у 2 рази більше ніж на другій. Скільки кущів росте на двох ділянках?
5. Від двох причалів,   розташованих на відстані 315 км., одночасно на зустріч один одному вийшли два теплоходи. Через 5 годин відстань між ними була 90 км. Швидкість одного теплохода 24 км/год. Знайдіть швидкість другого теплохода.

 

Контрольна робота № 3 за тему «Множення і ділення натуральних чисел»

Варіант 2

1. Виконати ділення і результат перевірити множенням:           2 008 609 · 401.
2. Виконайте дії:
   1. 29 857 : 73 + 574 · 89;
   2. 32 + (749 - 29) : 15.
3. Розв’яжіть рівняння:
   1. 531 648 : х = 526;
   2. 25 + (400 100 – 379 964) : 1.
4. В один магазин завезли 324 ц. картоплі, що в 6 разів більше, ніж у другий. Скільки картоплі завезли в другий магазин?
5. З одного пункту в протилежних напрямках одночасно виїхали мотоцикліст і велосипедист. Швидкість мотоцикліста 45 км/год., велосипедиста 15 км/год. На якій відстані один від одного вони будуть через 2 години.

 

Самостійна робота № 6 з теми «Промінь. Відрізок»

Варіант 1

1. Накреслити відрізки MN і QK  так , щоб MN = 5 см 2 мм,

    QK = 4 см 3 мм.

2. Позначити на числовому промені точки P (4) Q (6) A (9). За одиничний відрізок взяти одну клітинку зошита.
3. Накреслити відрізок завдовжки 8 см. Над одним кінцем відрізка написати число 0, над іншим – 16. поділити відрізок на 4 рівні частини. Позначити на отриманій шкалі числа 3; 7; 9; 14.
4. Дано відрізок АВ завдовжки 16 см. Точка М середина відрізка АВ, точка К – середина відрізка МВ. Знайти довжину відрізка АК.

 

Самостійна робота № 6 з теми «Промінь. Відрізок»

Варіант 2

1. Накреслити відрізки ХУ і ОА  так , щоб ХУ = 8 см 4 мм,

    АО = 3 см 3 мм.

2. Позначити на числовому промені точки А (4) Х (6) Q (10). За одиничний відрізок взяти одну клітинку зошита.
3. Накреслити відрізок завдовжки 9 см. Над одним кінцем відрізка написати число 0, над іншим – 18. поділити відрізок на 6 рівних частин. Позначити на отриманій шкалі числа 4; 8; 10; 16.
4. Точка М  середина відрізка АВ, точка К – середина відрізка МВ. Визначити довжину відрізка АК, якщо ВХ = 3 см.

 

Контрольна робота № 4 за тему «Промінь. Відрізок. Ламана. Кут»

Варіант 1

1. Побудуйте ламану RQSTX з чотирьох ланок так, щоб довжина ламаної дорівнювала 12 см 8 мм. Запишіть довжину кожної ланки. Виміряйте відстань та порівняйте її з довжиною ламаної; запишіть результат порівняння.
2. Точка А лежить на відрізку  MN довжиною 36 см. Знайдіть довжину відрізків MA і AN, якщо відрізок МА у 2 рази довший за відрізок AN.
3. Розгорнутий кут поділений на променем на два кути. Градусна міра одного з них 141°. Знайдіть градусну міру другого кута.
4. Точки А, В, С лежать на одній прямій. Яка з цих точок лежить між двома іншими якщо АВ = 33 мм, АС = 6 см, ВС = 2см 7 мм?

 

Контрольна робота № 4 за тему «Промінь. Відрізок. Ламана. Кут»

Варіант 2

1. Побудуйте ламану ABCDE з чотирьох ланок так, щоб довжина ламаної дорівнювала 10 см 2 мм. Запишіть довжину кожної ланки. Виміряйте відстань та порівняйте її з довжиною ламаної; запишіть результат порівняння.
2. Точка C лежить на відрізку  MN довжиною 24 см. Знайдіть довжину відрізків MC і CN, якщо відрізок МC у 3 рази довший за відрізок CN.
3. Розгорнутий кут поділений на променем на два кути. Градусна міра одного з них 52°. Знайдіть градусну міру другого кута.
4. Точки O, M, K лежать на одній прямій. Яка з цих точок лежить між двома іншими якщо OM = 3 см 6 мм, MK = 9 см,

    OK = 54 мм?

 

Самостійна робота № 7 з теми «Многокутники»

Варіант 1

1. Накресліть довільний трикутник;

а) прямокутний:

б) рівнобедрений.

2. Визначте вид трикутника за його кутами:

а) 34°; 127°; 19°;

б) 40°; 50°; 90° .

3. Одна сторона трикутника дорівнює 24 см, друга сторона на 18 см довша за першу, а третя у 2 рази коротша за другу. Знайти периметр трикутника.
4. У п’ятикутнику одна сторона 17 см, друга на 8 см більша, а третя дорівнює 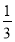суми першої і другої. Обчислити периметр цього п’ятикутника, якщо четверта сторона дорівнює п’ятій і на 5 см менша за другу.

 

Самостійна робота № 7 з теми «Многокутники»

Варіант 2

1. Накресліть довільний трикутник:

а) рівнобедрений;

б) тупокутний.

2. Визначте вид трикутника за його кутами:

а) 45°; 60°; 75°;

б) 95°; 85°; 5° .

3. Одна сторона трикутника дорівнює 12 см, друга сторона у три рази довша за першу, а третя на 8 см коротша за другу. Знайти периметр трикутника.
4. У чотирикутнику одна сторона дорівнює 20 см, друга у 2 рази менша, а третя становить 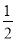суми першої і другої. Обчислити периметр чотирикутника, якщо четверта сторона дорівнює третій.

 

Самостійна робота № 8 з теми «Площа та об’єм»

Варіант 1

1. Виразіть;

а) в квадратних метрах:

 3 га 41 а;

б) в міліметрах.

 1 см²;

в) в кубічних сантиметрах:

 8 м³.

2. Довжина прямокутника 244 дм, ширина 150 дм. Знайти площу прямокутника і виразити її у квадратних метрах.
3. Ширина прямокутного паралелепіпеда дорівнює 18 см, довжина на 6 см більша, а висота – у два рази менша від довжини. Обчислити об’єм паралелепіпеда.
4. Висота проведена до основи трикутника, дорівнює 6 см і менша за цю основу в 6 разів. Обчислити площу трикутника.

 

Самостійна робота № 8 з теми «Площа та об’єм»

Варіант 2

1. Виразіть;

а) в квадратних метрах:

 5 км² 42 га;

б) в міліметрах:

 2 дм²;

в) в кубічних сантиметрах:

 4 дм³.

2. Довжина прямокутника 40 см, ширина 15 см. Знайти площу прямокутника і виразити її у квадратних дециметрах.
3. Висота прямокутного паралелепіпеда дорівнює 8 см, що на 5 см менше, ніж довжина і у два рази більше, ніж ширина. Обчислити об’єм паралелепіпеда.
4. Основа трикутника дорівнює 34 см і вона на 12 см більша за висоту, проведену до неї. Обчислити площу трикутника.

 

 

 

 

 

 

Контрольна робота № 5 за тему «Многокутники»

Варіант 1

1. Накресліть квадрат зі стороною 3 см 2 мм. Знайдіть його периметр і площу.
2. Накресліть прямокутник, довжина якого 4 см, а ширина у 2 рази менша за довжину. Обчисліть периметр і площу прямокутника.
3. Ребро куба дорівнює 5 м. Знайдіть об’єм куба.
4. Довжина прямокутного паралелепіпеда 8 дм. Ширина в 4 рази менша за довжину, а об’єм дорівнює 160 дм³. Знайдіть висоту.
5. Дано три прямокутники, сторони яких відповідно дорівнюють

 5 см і 3 см; 5 см і 4 см; 7 см і 2 см. Чи можна скласти квадрат із

          цих прямокутників? Якщо так, то знайдіть його периметр і площу. 

          Виконайте рисунок.

 

Контрольна робота № 5 за тему «Многокутники»

Варіант 2

1. Накресліть квадрат зі стороною 2 см 7 мм. Знайдіть його периметр і площу.
2. Накресліть прямокутник, ширина якого 2 см, а довжина у 3 рази більша від ширини. Обчисліть периметр і площу прямокутника.
3. Ребро куба дорівнює 7 м. Знайдіть об’єм куба.
4. Об’єм прямокутного паралелепіпеда 480 м³. Ширина - 4 м, довжина у два рази більша від ширини.. Знайдіть висоту.
5. Ящик має форму прямокутного паралелепіпеда з вимірами

    24 см, 32 см і 40 см. Його заповнили кубиками з ребром 4 см. 

   Скільки кубиків у ящику?

 

Самостійна робота № 9 з теми «Порівняння звичайних дробів»

Варіант 1

1. Розмістіть дроби в порядку їх зростання:

;

2. Допишіть пропущенні чисельники чи знаменники дробів у такі нерівності:

а) ;

б) ;

в) .

3. Тетянка зібрала 28 грибів, з них 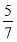грибів були білі. Скільки білих грибів зібрала Тетянка?
4. Петрик, Олег і Сашко зібрали 70 горіхів. Петрик зібрав 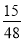усіх горіхів, а Сашко - 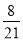решти. Скільки горіхів зібрав Олег.

 

Самостійна робота № 9 з теми «Порівняння звичайних дробів»

Варіант 2

1. Розмістіть дроби в порядку їх спадання:

;

2. Допишіть пропущенні чисельники чи знаменники дробів у такі нерівності:

а) ;

б) ;

в) .

3. Петрик піймав 6 окунів, що становить 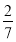усієї кількості риби, яку він піймав. Яку кількість риби піймав Петрик?
4. Наталка, Світлана та Юля збирали рослини для гербарію. Разом дівчатка зібрали 450 експонатів. Наталка зібрала 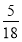усіх зібраних експонатів, Юля - 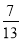решти. Скільки експонатів зібрала Світлана?

 

Самостійна робота № 10 з теми «Додавання і віднімання дробів

з однаковими знаменниками»

Варіант 1

1. Виконайте дії:

а) ;

б) ;

в) ;

г) ;

д) .

2. Розв’яжіть рівняння:

 ;  ;  .

3. Дід Панас продав 240 кг. Картоплі. Першого дня було продано 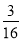картоплі, а другого дня - 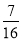. Скільки кілограмів картоплі було продано за два дні?

 

Самостійна робота № 10 з теми «Додавання і віднімання дробів

з однаковими знаменниками»

Варіант 2

1. Виконайте дії:

а) ;

б) ;

в) ;

г) ;

д) .

2. Розв’яжіть рівняння:

   ;  .

3. За перший місяць побудували 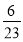дороги, а за другий - 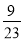. Скільки кілометрів дороги було побудовано за два місяці, якщо довжина всієї дороги становить 92 км.

 

Контрольна робота № 6 за тему «Звичайні дроби»

Варіант 1

1. Виділіть цілу частину із неправильного дробу:

2. Виконайте дії:

1. ;
2. ;
3. ;
4. .

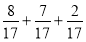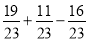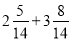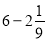3. Розв’яжіть рівняння:

1. ;
2. ;
3. .

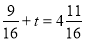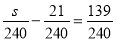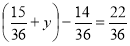4. Кролик з’їдає на день 48 г зерна. Це становить 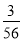маси його денного корму. Скільки кілограмів корму з’їдає кролик на день?
5. Турист пройшов 20 км; 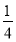шляху він йшов лісом, 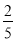- полем, а решту шляху – уздовж шосе. Скільки кілометрів пройшов турист уздовж шосе.

 

Контрольна робота № 6 за тему «Звичайні дроби»

Варіант 2

1. Виділіть цілу частину із неправильного дробу:

2. Виконайте дії:

1. ;
2. ;
3. ;
4. .

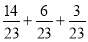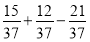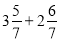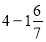3. Розв’яжіть рівняння:

1. ;
2. ;
3. .

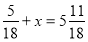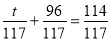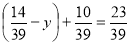4. Іванко прочитав 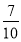книжки, що становить 56 сторінок. Скільки всього сторінок у книжці?
5. Швидкість польоту стрижа 100 км/год. Швидкість польоту ластівки становить 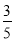швидкості польоту стрижа, а швидкість хруща – 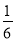швидкості ластівки. Знайдіть швидкості польоту ластівки та хруща.

 

 

Самостійна робота  № 11 з теми «Порівняння десяткових дробів»

Варіант 1

1. Запишіть у вигляді десяткового дробу:

 а) ;      б)  .

2. Запишіть частки у вигляді десяткових дробів:

 а)  175:10;     б)  286:100.

3. Запишіть у вигляді звичайного дробу 0,413.
4. Запишіть десятковими дробами числа:

 а) 32 цілі 7 сотих;    б)  12 цілих 4 тисячних.

5. Виділіть цілу і дробову частини та запишіть у вигляді десяткового дробу:

 .

6. Порівняйте дроби:

 а) 5,894 і 6,1;  б) 2,35 і 2,289;  в) 3,20 і 3,02;

 г) 0,34 і 0,340;  д) 0,023 і 0,23.

 

Самостійна робота  № 11 з теми «Порівняння десяткових дробів»

Варіант 2

1. Запишіть у вигляді десяткового дробу:

 а) ;      б)  .

2. Запишіть частки у вигляді десяткових дробів:

 а)  331:100;     б) 518:10.

3. Запишіть у вигляді звичайного дробу 0,218.
4. Запишіть десятковими дробами числа:

 а) 17 цілих 2 тисячних;    б)  43 цілих 5 сотих.

5. Виділіть цілу і дробову частини та запишіть у вигляді десяткового дробу:

 .

6. Порівняйте дроби:

 а) 3,895 і 5,2;  б) 0,23 і 0,230;  в) 0,034 і 0,34;

 г) 2,420 і 2,586;  д) 5,04 і 5,40.

 

Самостійна робота № 12 з теми «Додавання і віднімання десяткових дробів»

Варіант 1

1. Виконайте дії:

 а) 1,27 + 3,42;  б) 5,39+4,2;  в) 12,26+7,43.

2. Обчисліть використовуючи властивості додавання і віднімання десяткових дробів:

 а)  5,7-(27+2,3); б) 16,43-(5,6+7,43); в) (3,941+15,7)-12,7.

3. Розв’яжіть рівняння:

 а) (х-7,4)+2,8 = 9,1;   б) (у+3,716)-1,23=6,4.

4. Першого дня було зібрано 975,4 кг помідорів, другого – на 179,8 кг більше, ніж першого, а третього на 279 кг менше, ніж першого і другого дня разом. Скільки помідорів зібрали разом?

 

Самостійна робота № 12 з теми «Додавання і віднімання десяткових дробів»

 Варіант 2

1. Виконайте дії:

 а) 8,127 + 4,532; б) 517,126+4,43;  в) 17,02-6,3.

2. Обчисліть використовуючи властивості додавання і віднімання десяткових дробів:

 а)  14,9-(4,9+2,7); б) 15,87-(5,4+5,87); в) (4,563+12,8)-11,8.

3. Розв’яжіть рівняння:

 а) (х-9,4)+2,3 = 3,2;   б) (у+5,246)-2,43=7,1.

4. Автомобіль за перший день проїхав 357,85 км, за другий – на 19,36 км більше, ніж за перший, а третього дня – на 285,39 км менше, ніж за перший і другий день разом. Скільки кілометрів проїхав автомобіль за три дні?

 

Контрольна робота № 7 за тему «Десяткові дроби. Додавання і віднімання десяткових дробів»

Варіант 1

1. Виконайте дії: 62,3 – (41,24 + 13,029).
2. Розв’яжіть рівняння:

 а)  18,7-х=5,84; б) (3,2-х)+13,28=15,71.

3. Округліть до десятих числа:

 а) 3,6824;  б) 4,2128.

4. Знайдіть значення виразу в метрах:

 а) 23,4 м – 72 см; б) 3,4 м + 16 дм.

5. У трьох вагонах 149,3 т вантажу. У першому і другому вагонах разом 101,2 т, а в першому і третьому – 100,8 т. Скільки тонн вантажу в кожному вагоні?

 

Контрольна робота № 7 за тему «Десяткові дроби. Додавання і віднімання десяткових дробів»

Варіант 2

1. Виконайте дії: 75,5 – (36,43 + 28,065).
2. Розв’яжіть рівняння:

 а)  х+12,49=15,3; б) (4,3-у)+11,37=13,2.

3. Округліть до сотих числа:

 а) 5,6492;  б) 18,3724.

4. Знайдіть значення виразу в тоннах:

 а) 5,3 т- 543 кг; б) 2,5 т + 23 ц.

5. Довжина однієї сторони трикутника 16,7 м, це на 8,27 м більше, ніж довжина його другої сторони, а довжина третьої сторони на 1,88 м. більша ніж другої. Знайдіть периметр трикутника.

 

Самостійна робота № 13 з теми «Множення десяткових дробів»

Варіант 1

1. Обчисліть:

 а) 2,4 · 3,6; б) 9,16 ·5,5; в) 0,018 · 0,65;

 г) 6,58 ·10; д) 6,3 ·100; е) 35,1 ·0,01.

2. Знайдіть значення виразу:

 а)  (0,5 ·7) ·20;  б) 3,4 ·1,6+6,6 ·1,6.

3. Дід Остап продав 15,8 кг вишень по 2,05 грн за кілограм і 20,5 кг слив по 1,6 грн за кілограм. За які фрукти він уторгував більше грошей і на скільки?
4. Із 60 кидків м’ячем по воротах під час гандбольного матчу 0,8 усіх кидків були результативними. Скільки разів м’яч не влучив у ворота?

 

Самостійна робота № 13 з теми «Множення десяткових дробів»

Варіант 2

1. Обчисліть:

 а) 2,7 · 5,3; б) 0,37 ·1,9; в) 2,376 · 0,42;

 г) 6,58 ·100; д) 1 ·10000; е) 6,58 ·0,1.

2. Знайдіть значення виразу:

 а)  (0,2 · 12) · 50;  б) 4,49 · 15,2 – 4,49 · 5,2.

3. Вирушивши у похід, група школярів 8,5 год. йшла пішки зі швидкістю 4,2 км/год і 9,2 год пливла по річці на плоту зі швидкістю 3,5 км/год. Який шлях, по суші чи по річці, вона подолала більший і на скільки?
4. У класі 40 учнів. У хорі співають 0,25 усіх учнів класу. Скільки дітей не співають у хорі?

 

 

 

 

 

Самостійна робота № 14 з теми «Ділення  десяткових дробів на натуральне число»

Варіант 1

1. Обчисліть:

 а) 2,4 : 3; б) 5,16 : 10; 

 в) 39,857 : 100; г) 126,385 : 25.

2. Розв’язати рівняння:

 а)  7 х = 21; б) 6 у + 3,4 = 38,8.

3. Знайдіть значення виразу: 45 – 46,2 : 3 + 0,072.
4. Скільки коштує 1 кг цукерок, якщо за 0,6 кг печива по 5,85 грн за 1 кілограм і за 2 кг цукерок заплатили 34,71 грн?

 

Самостійна робота № 14 з теми «Ділення  десяткових дробів на натуральне число»

Варіант 2

1. Обчисліть:

 а) 1,8 : 6; б) 5,45 : 100; 

 в) 83,579 : 10; г) 25,036 : 44.

2. Розв’язати рівняння:

 а)  6 х = 0,42; б) 7 у + 7,1 = 50,5.

3. Знайдіть значення виразу: 40 – 23,2 : 8 + 0,07.
4. У двох кошиках і чотирьох однакових ящиках складено 73,72 кг апельсинів.  У кожному кошику по 6,4 кг апельсинів. Скільки апельсинів у кожному ящику?

 

 

 

Контрольна робота № 8 за тему «Множення десяткових дробів. Ділення десяткових дробів на натуральне число»

Варіант 1

1. Знайдіть значення виразу:

 а) 10,3 · 8,4 – 3,26 · 10,3; б) (32,7-8,49) : 30 – 0,657. 

2. Розв’язати рівняння: 2х + 0,49 = 7,23.
3. Порівняйте значення виразів:

 3,6 · 8,2- 3,1²  і 65,3 : 4 + 3,585.

4. Із пунктів А і В одночасно назустріч один одному виїхали два мотоциклісти. Швидкість одного з них 40,6 км/год, а другого – 49,6 км/год. Мотоциклісти зустрілися через три години. Знайдіть відстань від пункту А до пункту В.
5. Розв’яжіть рівняння: (3z – 15,8) · 4 – 14,8.

 

Контрольна робота № 8 за тему «Множення десяткових дробів. Ділення десяткових дробів на натуральне число»

Варіант 2

1. Знайдіть значення виразу:

 а) 8,11· 3,2 – 5,24 · 3,2; б) (56,3-7,94) : 60 – 0,506. 

2. Розв’язати рівняння: 2х – 6,25 = 3,8.
3. Порівняйте значення виразів:

 5,3 · 0,64 + 2,6² і 59,4 : 3 - 9,648.

4. Мотоцикліст і велосипедист одночасно виїхали в одному напрямі. Швидкість мотоцикліста 64,7 км/год, а велосипедиста 15,8 км/год. Яка відстань між ними буде через 4 години руху?
5. Розв’яжіть рівняння: (х : 24 + 7,56) · 17 – 140,4.

 

 

Самостійна робота № 15 з теми «Ділення десяткових дробів»

Варіант 1

1. Перетворіть у десятковий дріб:

 а) ; б) .

2. Обчисліть:

 а) 28,8 : 1,8; б) 8,1 : 2,25; в) 4,928 : 0,16;

 г) 0,22274 : 0,43; д) 8 : 0,1; е) 4 : 0,001. 

3. Розв’язати рівняння:

 а)  у  · 4,9 = 2,92;  б) 7,8а + 5,4а = 3,3.

4. Поїзд проїхав 135,8 км за 2,8 год. Скільки кілометрів він проїде за 6,2 год з тією самою швидкістю?

Самостійна робота № 15 з теми «Ділення десяткових дробів»

Варіант 2

1. Перетворіть у десятковий дріб:

 а) ; б) .

2. Обчисліть:

 а) 45,6 : 2,4; б) 60 : 1,25; в) 7,488 : 3,12;

 г) 6,1244 : 0,061; д) 5 : 0,01; е) 54 : 0,1. 

3. Розв’язати рівняння:

 а)  9,2 · у  = 3,68;  б) 4,9т – 0,1т = 3,84.

4. За 3,6 кг цукерок заплатили 45,36 грн. Скільки треба заплатити за 6,5 кг таких цукерок?

 

 

 

Самостійна робота № 16 з теми «Дії з десятковими дробами»

Варіант 1

1. Знайдіть значення виразу: (299,3 : 14,6 – 9,62) · 3,5.
2. Автобус ішов 0,8 години зі швидкістю 68,7 км/год, а зі швидкістю 90,4 км/год – 2 год. Який шлях пройшов автобус?
3. Знайдіть ширину прямокутного паралелепіпеда, об’єм якого дорівнює 13,5 м³, висота – 2,25 м, а довжина – 1,6 м.
4. Розв’яжіть рівняння: 12,4 +8,3х + 1,5х = 34,94.
5. Купили два кошики полуниць, загальною масою 8,36 кг. У першому кошику полуниць на 1,22 кг більше, ніж у другому. Скільки полуниць у кожному кошику? Скільки заплатили за покупку, якщо 1 кг полуниць коштує 2,75 грн?

 

Самостійна робота № 16 з теми «Дії з десятковими дробами»

Варіант 2

1. Знайдіть значення виразу: (18,48 : 1,68 – 9,68) · 0,2.
2. Катер плив озером 0,3 години зі швидкістю 16,3 км/год і за течією ріки – 3 години. Знайдіть шлях катера, якщо швидкість течії ріки 2,3 км/год.
3. Знайдіть довжину прямокутного паралелепіпеда, об’єм якого дорівнює 57,792 мм³, ширина – 4,2 см, а висота – 1,6 см.
4. Розв’яжіть рівняння: 5,4z – 2,6z – 17,6 = 11,8.
5. Із двох пунктів, відстань між якими 9 км, одночасно назустріч один одному вийшли два лижники. Один із них рухався із швидкістю 7,25 км/год, а другий із швидкістю. В 1,5 разу більшою. Через який час лижники зустрінуться?

 

Контрольна робота № 9 за тему «Ділення десяткових дробів. Дії з десятковими дробами»

Варіант 1

1. Знайдіть значення виразу:

 а) 0,63 : 0,21 + 0,8 · 12,5;  б) (1,2 · 7,4 + 2,8) : 0,2.

2. Розв’яжіть рівняння: 0,48 · х = 1,68.
3. Довжина прямокутника 5,4 м, а ширина становить 0,8 його довжини. Знайдіть площу прямокутника; результат округліть до десятих.
4. Поле площею 314,4 га засіяли гречкою і горохом. Причому поле. Зайняте гречкою. У 3 рази більше від поля зайнятого горохом. Скільки гектарів засіяли гречкою і горохом?
5. Розв’яжіть рівняння: (0,4х – 27,5) · 0,25 = 2,745.

 

Контрольна робота № 9 за тему «Ділення десяткових дробів. Дії з десятковими дробами»

Варіант 2

1. Знайдіть значення виразу:

 а) 0,96 : 0,16 + 0,04 · 2,5;  б) (7,4 ·  2,8 – 7,4 · 1,9) : 0,4.

2. Розв’яжіть рівняння: 64,45 : х = 2,5.
3. Площа прямокутника 74,1 см², а його ширина 6 см. Знайдіть довжину прямокутника; результат округліть до десятих.
4. Із двох сіл, відстань між якими 7,76 км, одночасно назустріч один одному вийшли два пішоходи; через 0,8 години вони зустрілися. Швидкість одного з пішоходів 5,2 км/год. Знайдіть швидкість другого пішохода.
5. Розв’яжіть рівняння: (0,8х + 19,4) · 0,2 = 1,928.

 

Самостійна робота № 17 з теми «Середнє арифметичне кількох чисел»

Варіант 1

1. Знайти середнє арифметичне чисел:

 а) 1,1 і 2,9;  б) 0,289 і 0,32.

2. Турист за 3 години пройшов 18 км, а за наступні 2 години – 14 км. Обчислити середню швидкість туриста.
3. Мотоцикліст 4 год рухався зі швидкістю 35 км/год, а 2 год – зі швидкістю 31 км/год. Яка його середня швидкість?
4. Одне з чисел на 134 більше від другого, а їх середнє арифметичне дорівнює 133. Знайти ці числа.

 

Самостійна робота № 17 з теми «Середнє арифметичне кількох чисел»

Варіант 2

1. Знайти середнє арифметичне чисел:

 а) 3,5 і 2,5;  б) 84,2 і 39,7.

2. За перші 4 години пішохід пройшов 20,6 км, а за наступні дві години – 10 км. Обчислити середню швидкість руху пішохода.
3. Автомобіль 3 год рухався зі швидкістю 62 км/год, а наступні 2 год – зі швидкістю 56 км/год. З якою середньою швидкістю рухався автомобіль?
4. Одне з чисел менше від другого на 67, а їх середнє арифметичне дорівнює 116,5. Знайти ці числа.

 

 

 

Самостійна робота № 18 з теми «Відсотки»

Варіант 1

1. Запишіть у вигляді десяткового дробу:

 а) 8 %; б) 20 %; в) 140 %; г) 2,4 %.

2. Запишіть у відсотках:

 а) 0,24; б)0,04; в)0,4; г) 1,6;  д) 8.

3. Знайдіть:

а) 1 % від числа 4;  б) 15 % від числа 60; в) 120 % від числа 50.

4. Знайдіть число, якщо:

 а) 54 % цього числа дорівнюють 81;

 б) 280 % цього числа дорівнюють 70.

5. За два дні продали 125 кг яблук, причому за перший день продали 46 % яблук. Скільки кілограмів яблук продали за другий день?
6. Купили сир і ковбасу, причому за сир заплатили 24,3 грн, що становить 60 % від вартості усієї покупки. Скільки коштує вся покупка? Скільки гривень заплатили за ковбасу?

 

Самостійна робота № 18 з теми «Відсотки»

Варіант 2

1. Запишіть у вигляді десяткового дробу:

 а) 5 %; б) 52 %; в) 160 %; г) 3,2 %.

2. Запишіть у відсотках:

 а) 0,58; б)0,8; в)0,08; г) 2,5; д) 9.

3. Знайдіть:

а) 1 % від числа 76; б) 30 % від числа 120; в) 156 % від числа 62.

4. Знайдіть число, якщо:

 а) 12 % цього числа дорівнюють 4,8;

 б) 104 % цього числа дорівнюють 260.

5. У печері розбійників Алі-Баба знайшов 480 кг золота і срібла. Золото становило 45 % скарбу. Скільки кілограмів срібла знайшов Алі-Баба?
6. Після варіння м’яса вихід становить 62 % від маси свіжого м’яса. Скільки треба взяти свіжого м’яса, щоб отримати 4,96 кг вареного?

 

Контрольна робота № 10 за тему «Середнє арифметичне кількох чисел. Задачі на відсотки. Масштаб»

Варіант 1

1. Ділянка на плані зображується прямокутником, довжини сторін якого дорівнюють 16 см і 10 см. Масштаб плану 1 : 100. Знайдіть розміри ділянки.
2. Знайдіть середнє арифметичне чисел: 36,2; 48,1; 23,7; 54,5.
3. При виробництві цукру із цукрового буряку вихід цукру становить 16 % від маси буряку. Скільки цукру вийде із 400 ц буряку?
4. У руді міститься 4,5 % міді. Скільки потрібно взяти руди, щоб одержати 2,25 т міді?
5. Знайдіть число а, якщо середнє арифметичне чисел 4,6; 7,2 і а дорівнює 5,2.
6. Туристи за три дні пройшли 49 км. Першого дня вони пройшли 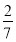всього маршруту, а другого – 80 % решти. Скільки кілометрів туристи пройшли третього дня?

 

 

Контрольна робота № 10 за тему «Середнє арифметичне кількох чисел. Задачі на відсотки. Масштаб»

Варіант 2

1. Відстань між містами 270 км. На карті ця відстань зображується відрізком завдовжки 13,5 см. Визначте масштаб карти.
2. Знайдіть середнє арифметичне чисел: 14,3; 19,7; 21,8.
3. Матері 25 років. Вік сина становить 20 % віку матері. Скільки років синові?
4. В автопарку 22 % всіх машин становлять вантажівки. Скільки всього машин в автопарку, якщо вантажівок 66?
5. Знайдіть число b, якщо середнє арифметичне чисел 2,6; 8,5 і b дорівнює 5,9.
6. Поле площею 40 га засадили капустою, морквою і цибулею. Капуста займає 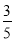 усієї площі., а морква – 75 % решти. Яку площу відведено під цибулю?

 

 

Контрольна робота  № 11 за тему «Повторення»

Варіант 1

1. Обчисліть: 2,66 : 3,8 – 0,81 + 0,0372.
2. У магазині було 240 кг фруктів. За день продали 55 % фруктів. Скільки кілограмів фруктів залишилося?
3. Знайдіть довжину прямокутного паралелепіпеда, об’єм якого дорівнює 25,5 дм³, ширина 16 см, висота – 3,5 дм.
4. Порівняйте  20 % від 16,4 т і 0,8 від 4,1 т.
5. Периметр трикутника 10,7 см. Перша сторона трикутника у 2 рази більша від другої, а третя – менша за першу сторону на 1,3 см. Знайдіть сторони трикутника.
6. Побудуйте кути МОК і КОС, якщо МОК = 110°,  КОС = 46°. Чому може дорівнювати градусна міра кута СОМ?

 

Контрольна робота  № 11 за тему «Повторення»

Варіант 2

1. Обчисліть: (299,3 : 14,6 – 9,62) · 3,5 + 72,2.
2. У цистерні було 850 л молока, 52 % молока розлили в бідони. Скільки літрів молока залишилося в цистерні?
3. Розв’яжіть рівняння: 12 + 8,3х + 1,5х = 95,3.
4. Порівняйте 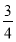від 20,8 ц і 40 % від 39 ц..
5. власна швидкість теплохода 24,5 км/год., швидкість течії річки 1,3 км/год. Спочатку теплохід плив 0,3 год. озером, а потім 2,5 год. проти течії річки. Який шлях пройшов теплохід за весь час руху?
6. Промінь АР поділяє прямий кут САN на два кути так, що градусна міра кута NAP становить 0,3 градусної міри кута CAN. Знайдіть градусну міру кута PAN. Виконайте креслення.