ДИНАМІЧНІ ПОБУДОВИ В СЕРЕДОВИЩІ GEOGEBRA НА ПРИКЛАДІ РІВНЯНЬ З ПАРАМЕТРАМИ, ЩО МІСТЯТЬ ЗНАК МОДУЛЯ

Валентина Дармосюк, Маргарита Зайцева

ДИНАМІЧНІ ПОБУДОВИ В СЕРЕДОВИЩІ GEOGEBRA НА ПРИКЛАДІ РІВНЯНЬ З ПАРАМЕТРАМИ, ЩО МІСТЯТЬ ЗНАК МОДУЛЯ

Сьогодні значна увага приділяється використанню комп'ютерів та інформаційних технологій для посилення візуальної та експериментальної складової навчання математики, реалізації практичної спрямованості у навчанні математики.

GeoGebra – інтерактивне творче середовище, засноване на принципах динамічної геометрії та комп’ютерної алгебри, призначене для створення інтерактивних креслень (моделей) з математики, що поєднують в собі конструювання, моделювання, динамічне варіювання та експеримент. Застосування програмно-графічного комплексу GeoGebra дає можливість реалізації розвиваючого навчання, ідеї моделювання і прикладної спрямованість курсу математики. На прикладі завдань з параметрами, що містять знак модуля, розглянемо можливості динамічного математичного середовища GeoGebra та доцільність його застосування в навчальному процесі.

Загальних методів розв’язання задач, у яких присутні числові параметри, не існує. У кожному конкретному випадку підхід до їхнього розв’язання вибирається виходячи зі структури завдання та потребує аналізу отриманого розв’язку залежно від конкретного значення параметра.

В основу розв’язання задач із параметром може бути покладений наступний принцип: значення параметра вважається довільно фіксованим, а потім шукається розв’язок задачі так, як розв’язок рівняння з одним невідомим (або системи рівнянь із двома невідомими). Відповіддю повинне бути перерахування всіх розв’язків для кожного допустимого значення параметра, що вимагає проведення дослідження. При цьому множину значень параметра розбивають на підмножини тими значеннями параметра, при яких або при переході через які відбувається якісна зміна рівняння.

Існують різні способи розв’язання задач із параметрами, серед яких найбільш часто використовують алгебраїчний, функціонально-аналітичний і графічний способи. Графічний метод вирізняється красотою і наочністю, але, як відомо, потребує гарного вміння працювати з графіками. Адже суть методу полягає в тому, що задачу зводять до з’ясування взаємного розташування графіків рівнянь.

Розглянемо можливості та функціонал середовища GeoGebra на прикладах.

Завдання 1. Розв’язати рівняння . У відповідь записати найбільше значення а, за якого рівняння має корені.

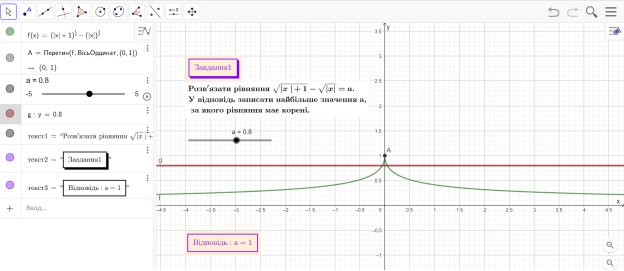
Рис.1

Провівши попередні дослідження, ми представили запропоноване рівняння як систему двох функцій . Спільні точки двох графіків і будуть розв’язками даної системи. Представлена на Рис. 1 динамічна модель показує, що змінюючи значення параметра система (а отже і запропоноване рівняння) може мати розв’язки або не мати їх. Найбільше значення параметра , при якому рівняння матиме корені буде значення 1.

Завдання 2. Скільки розв’язків має рівняння в залежності від параметра а?

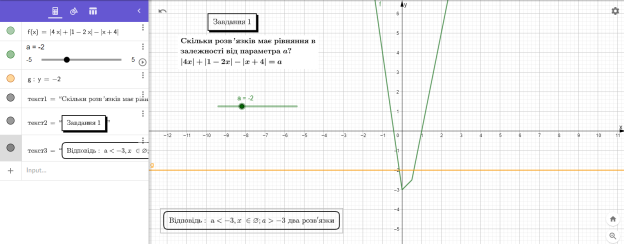
Рис. 2

Представлена на Рис. 2 динамічна модель показує, що змінюючи значення параметра , запропоноване рівняння може мати розв’язки або не мати їх. Рівняння буде мати розв’язки при , при а=-3 один розв’язок, при .

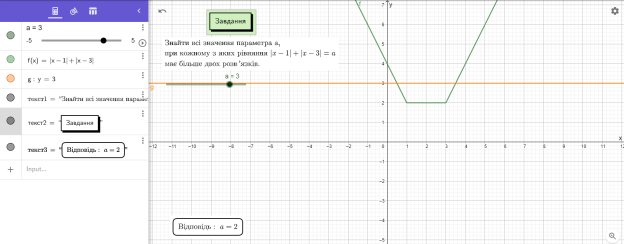
Завдання 3. Знайти всі значення параметра а, при кожному з яких рівняння має більше двох розв’язків.

Рис. 3

Представлена на Рис. 3 динамічна модель показує, що змінюючи значення параметра рівняння може при а >2  маємо 2 розв’язки: при , при і маємо нескінченну кількість розв’язків.

Отже, процес інформатизації освіти, підтримуючи інтеграційні тенденції пізнання закономірностей предметних областей і навколишнього середовища, актуалізує розробку підходів до використання потенціалу інформаційних технологій для розвитку особистості школярів. Цей процес підвищує рівень активності і мотивацію учнів, розвиває здібності альтернативного мислення, формування умінь розробляти стратегію пошуку розв’язків як навчальних, так і практичних завдань, дозволяє прогнозувати результати реалізації прийнятих рішень на основі моделювання досліджуваних об'єктів, явищ, процесів і взаємозв'язків між ними. Використання на уроках середовищ динамічної математики, таких як GeoGebra, змінює традиційні методики викладання, дозволяючи підвищити інтерес учнів до предмету, тобто сприяє кращому засвоєнню навчального матеріалу. На прикладі розв’язання рівняння з параметром, що містить модуль, графічним способом проілюстровано ефективність застосування середовища GeoGebra для реалізації принципу наочності, можливості проведення учнями самостійних досліджень.