Розвязування задач з параметрами
Методичні рекомендації для вчителів, що працюють в класах з поглибленим вивченням математики що до вивчення задач з параметрами.Робота містить збірник завдань, наведено приклади розвязків.
1
Математична майстерня.
Практикум з розв'язування завдань з параметрами.
Завдання з параметрами - проблема для більшості випускників на ЗНО. Але задачі з параметрам сприяють розвитку логічного мислення, підвищують математичну культуру школярів. І часто зміст математичної задачі с параметрами не виходить за межі шкільної програми, але учні не готові розв'язувати таке завдання без попередньої підготовки. Досвід показує, що починати знайомство з параметрами треба як раніше, і частіше повертатися до таких задач протягом усіх років навчання у школі. Про параметри написано багато чудових книжок, але мені хочеться запропонувати вам розв’язання проблеми з точки зору учителя
Література:
- Горнштейн П.І., Полонський В.Б., Якір М.С. Задачі з параметрами, Тернопіль, 2004
- Апостолова Г.В., Ясінський В.В. Перші зустрічі з параметрами. 2004
- Мерзляк А.Г., Полонський В.Б., Якір М.С. Алгебра 8, 9, 10, 11
7 клас
Тема: Лінійні рівняння
-
Дано рівняння

а) рівняння має додатній корінь?
б) рівняння має корінь, менший за -2, але більший за -3?
-
Знайти усі цілі a, при яких корінь рівняння
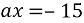
цілим числом.
-
При яких значення b рівняння
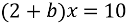
а) має корінь 5;
б) не має коренів?
- Розв’язати рівняння:
а) ![]() г)
г) ![]()
б) ![]() д)
д) ![]()
в) ![]() е)
е) ![]()
8 клас
Тема: Рівняння, що зводяться до лінійних.
-
Дано рівняння
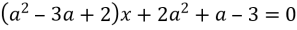
а) При яких значеннях ![]()
![]()
б) При яких ![]()
в) При яких ![]()
г) При яких ![]()
Вкажіть цей розв’язок.
-
Розв’яжіть рівняння.
-
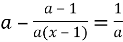 ; б)
; б) 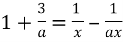
-
Тема: Нерівності.
Для кожного значення ![]()
-
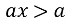
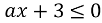
б) ![]() д)
д) ![]()
в) ![]() е)
е) ![]()
Тема: Функція
Скільки розв’язків в залежності від значення параметра ![]()
а) ![]() д)
д) ![]()
б) ![]() е)
е) ![]()
в) ![]() є)
є) ![]()
г) ![]() ж)
ж) ![]()
9 клас
Тема: Квадратична функція.
-
При якому значені

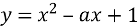 зростає на проміжку
зростає на проміжку 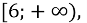 спадає на
спадає на 
-
При яких значеннях
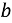
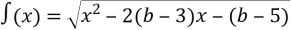 є числова пряма?
є числова пряма?
-
При яких значеннях

![]() складається з однієї точки?
складається з однієї точки?
-
При яких значеннях

1)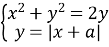 2)
2) 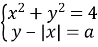
а) має два розв’язки?
б) має три розв’язки?
- Розв’язати рівняння
а) ![]()
б) ![]()
в) ![]()
г) ![]()
-
Скільки розв’язків в залежності від параметра а має система
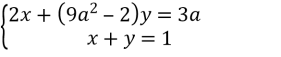 ?
?
Знайдіть ці розв’язки.
7. При яких с нерівність ![]()
виконується при всіх x?
У 10-11 класах повторюють усі типи завдань, що містять параметри і були розглянуті у 7-9 класах, але на більш високому рівні.
Зазвичай у рівності або нерівності буквами позначають невідомі. Іноді рівняння (нерівність) крім букв, що позначали невідомі, містять інші букви, які називають параметрами. Тоді ми маємо справу не з одним, а з нескінченною множиною рівнянь (нерівностей).
При цьому буває, що при одних значеннях параметра рівняння не має розв’язків, при інших – має тільки один корінь і т ін.
Розв’язати рівняння (нерівність) з параметром – для кожного значення параметра знайти множину значень змінної, що задовольняє дане рівняння (нерівність).
Розглянемо деякі завдання з параметрами, що були запропоновані на ДПА у 2012 (2011) роках.
1. Рівняння.
Для кожного значення параметра a розв’яжіть рівняння.
1) ![]()
Якщо ![]()
![]()
![]() ,
, ![]()
![]()
![]()
![]()
Враховуючи (*) ![]() ,
, ![]() ,
,
![]() ,
, ![]()
Якщо x<1 (**), то ![]()
![]()
![]()
![]()
![]()
![]()
Враховуючи (**) ![]() ,
, ![]()
![]()
Якщо ![]()
![]() ,
,
![]()
х=1
Якщо ![]()
![]() ,
,
![]() ,
, ![]()
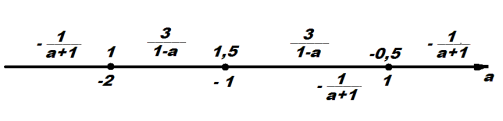 Якщо
Якщо ![]()
![]() , x=-0,5
, x=-0,5
Відповідь: при ![]() ;
;
при ![]() ;
;
при ![]() ;
;
при ![]()
при ![]()
при ![]()
Інакше:
Відповідь:
![]()
![]() ,
, ![]()
![]()
2) |х2-4|+|х2-9|=а
Нехай ![]() (*), тоді
(*), тоді ![]() а)
а) ![]()
![]()
б) ![]()
в) ![]() ),
),
![]() ,
,
при ![]() при
при ![]()
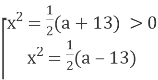
![]()
![]()
![]()
![]()
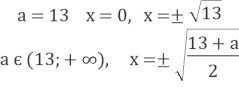 Відповідь:
Відповідь:
при ![]()
при ![]()
при ![]()
![]()
при ![]()
при ![]()
3) ![]() має один корінь
має один корінь
Нехай ![]() (*), тоді
(*), тоді ![]()
![]()
![]()
![]()
а) ![]() ,
,
![]() ,
, ![]()
б) ![]()
![]()
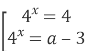
![]()
![]()
![]()
4) Для кожного значення параметра a розв’яжіть рівняння 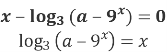
![]()
![]() ,
,
![]()
![]()
б) ![]()
в) ![]() , оскільки
, оскільки ![]()
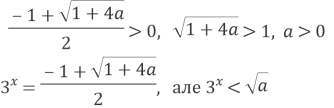
![]()
![]() ,
,
![]() ,
, ![]()
![]()
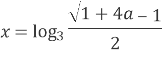 Відповідь: при
Відповідь: при ![]()
при ![]()
5) Знайдіть усі значення параметра a, при кожному з яких рівняння ![]() має два корені:
має два корені: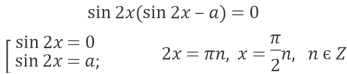
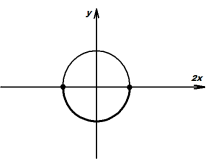 Оскільки
Оскільки ![]() , то перше рівняння сукупності дає два корені,
, то перше рівняння сукупності дає два корені, ![]() , тому друге рівняння сукупності або має такі самі корені: a=0, або на [
, тому друге рівняння сукупності або має такі самі корені: a=0, або на [![]() коренів не має
коренів не має
x є [ ![]()
![]()
![]()
Відповідь: ![]()
2. Нерівності
1) Для кожного значення a розв’яжіть нерівність ![]()
![]() або
або ![]()
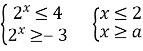
![]()
![]()

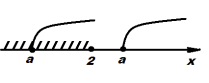
![]()
![]()
![]()
![]()
![]()
![]() ;
;
![]()
![]()
2) ![]()
 ОДЗ:
ОДЗ: ![]()
![]() )
)
![]()
![]()
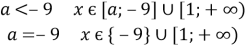 -9<a<1
-9<a<1 ![]()
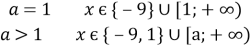 Відповідь: при
Відповідь: при ![]()
при -9≤a≤1 ![]()
при ![]()
![]()
ОДЗ![]()
Оскільки ![]()
![]()
![]()
![]()
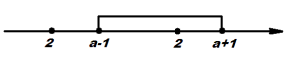 Врахуємо ОДЗ
Врахуємо ОДЗ
а) ![]() б)
б) ![]()
в) ![]()
![]()
г) ![]()
![]()
Відповідь: ![]()
![]()
![]()
![]() a)
a) ![]()
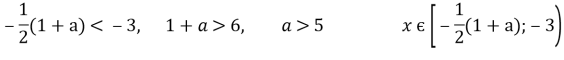 б)
б) ![]()
![]() ,
,
![]()
Відповідь: при ![]()
при![]()
II Спосіб
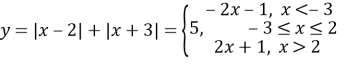
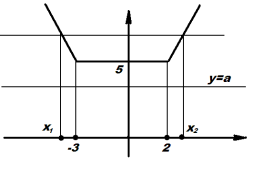 При
При ![]()
при ![]()
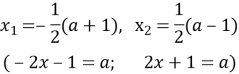
5) ![]()
![]()
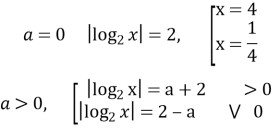
![]()
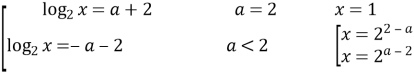
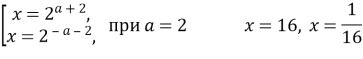 Відповідь: при
Відповідь: при ![]()
при ![]() при
при ![]()
при ![]()
при ![]()
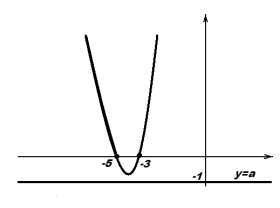 3. Графічні розв’язування рівняння (нерівностей) з параметрами.
3. Графічні розв’язування рівняння (нерівностей) з параметрами.
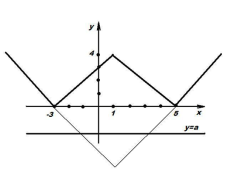
1) Для кожного значення a вкажіть, скільки точок перетину мають графік функції ![]() і пряма у=а
і пряма у=а
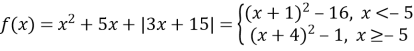
![]()
![]()
![]()
![]()
 2) Розв’яжіть рівняння
2) Розв’яжіть рівняння
![]()
![]() а)
а) ![]()
![]()
![]()
![]()
г) ![]()
д) ![]() Відповідь:
Відповідь: ![]()
![]()
![]()
![]()
![]()
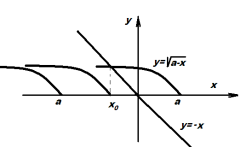 3) Для кожного значення a розв’яжіть нерівність
3) Для кожного значення a розв’яжіть нерівність ![]()
![]()
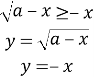
Якщо a>0, то x є [x0![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
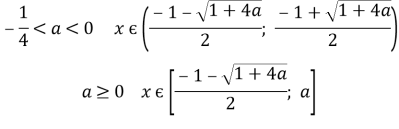 Відповідь: при
Відповідь: при ![]() ,
,
при ![]()
при ![]()
при ![]()
Домашнє завдання
1) Знайдіть найбільше значення параметра a, при якому рівняння ![]() має рівно три різні корені
має рівно три різні корені
Відповідь: 16
2) Знайдіть найбільше ціле a, при якому рівняння ![]() має додатній корінь. Відповідь: 9
має додатній корінь. Відповідь: 9
3) Знайдіть найменше значення параметра a, при якому система 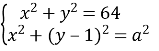 має єдиний розв’язок
має єдиний розв’язок
Відповідь: - 9
4) Розв’язати рівняння:
a) ![]() Відповідь: -4,5
Відповідь: -4,5
б) ![]() Відповідь:
Відповідь: ![]()
![]() 5) Розв’яжіть нерівність
5) Розв’яжіть нерівність ![]()
Відповідь: при ![]()
при а=0 ![]()
при ![]()
6) При якому значенні a (a - найменше ) рівняння
![]() має хоча б один корінь? Відповідь: a=4,5
має хоча б один корінь? Відповідь: a=4,5
7) Знайдіть найменше значення a, при якому має розв’язки рівняння ![]() Відповідь: a=-4,5
Відповідь: a=-4,5
8) Знайдіть значення a, при кому корінь рівняння
![]() належить проміжку
належить проміжку ![]()
Відповідь: -23,3
-
-
Дякую, дуже корисна розробка.


про публікацію авторської розробки
Додати розробку
