Розв’язування задач за допомогою систем лінійних рівнянь із двома змінними

Тема: Розв’язування задач за допомогою систем лінійних рівнянь із двома змінними

Дата:                                                                                                            Клас: 7

Мета:

навчальна: формування вмінь учнів розв'язувати задачі складанням системи рівнянь; ознайомити учнів із технологією розв’язування текстових задач складанням систем лінійних рівнянь із двома змінними; виробити первинні вміння щодо застосування цієї технології під час розв’язування найпростіших задач; вдосконалити вміння застосовувати різні способи розв’язування систем лінійних рівнянь із двома змінними;

розвиваюча: розвивати логічне мислення, пам’ять, зосередженість, уважність, допитливість, впевненість в своїх силах;

виховна: виховувати самостійність, наполегливість, культуру математичних записів, інтерес до математики.

Тип уроку: комбінований

Обладнання: Аглебра 7 кл.: Підруч. для загальноосвіт. навч. закл./ О.С. Істер. – Києв : Генеза, 2015. – 256 с.

Хід уроку:

1. Організаційний момент

Привітання, перевірка присутності учнів на уроці.

2. Перевірка домашнього завдання

Перевірити наявність виконаного домашнього завдання і відповісти на запитання, які виникли в учнів при його виконанні.

3. Актуалізація опорних знань

Математичний диктант

Варіант 1	Варіант 2
Опишіть за допомогою рівняння ситуацію:
1) сума чисел x і y дорівнює 20; (x+y=20) 2) число x удвічі більше за число y; (2x) 3) середнє арифметичне чисел x і y дорівнює 17; ((x+y):2=17) 4) периметр квадрата зі стороною x на 5 більший за периметр квадрата зі стороною y;   (x+5) 5) за 3 пиріжки вартістю x грн кожний і 1 булочку вартістю y грн заплатили 9,5 грн. (3x+y=9,5)	1)різниця чисел x і y дорівнює 30; (x-y=30) 2) число x утричі менше від числа y; (x:2) 3) подвоєна сума чисел x і y дорівнює 16;(2xy=16) 4) олівець вартістю x грн дешевший, ніж ручка вартістю y грн, на 0,1 грн; (0,1x) 5) груша масою x г і 5 яблук масою y г кожне мають загальну масу 900 г. (x+5y=900)

 

4.    Повідомлення теми і мети уроку

Сьогодні на уроці ми сформуємо вміння розв'язувати задачі складанням системи рівнянь. Ознайомимося із технологією розв’язування текстових задач складанням систем лінійних рівнянь із двома змінними.

5.        Мотивація навчальної діяльності

Математика завоювала авторитет серед різних наук тим, що зуміла сформулювати і розв’язати ті задачі, які виникають у різноманітніших видах людської діяльності. Колись давно способами розв’язання задач було звичайне прикидання «на око» або перебирання всіх можливих варіантів. Проте навіть  з простої умови задачі складно з’ясувати, який варіант розв’язання найкращий, а всі перебрати практично неможливо.

Застосування рівнянь спрощує розв’язування багатьох текстових задач. Розв’язування багатьох задач можна звести  до розв’язування  системи двох рівнянь їз двома змінними.                   

6. Сприйняття й усвідомлення нового матеріалу

Задача 1. Учень задумав два числа, сума яких дорівнює 100, а різниця – 26. Які числа задумав учень?  

Розв’язування за допомогою рівняння з однією змінною:

 Нехай х – перше число, тоді (х – 26) – друге число. Оскільки їх сума дорівнює 100, то маємо рівняння:

х + (х – 26) = 100

2х = 126

х = 63

Відповідь: перше число 63, друге – 37.

Розв’язування за допомогою системи рівнянь:

Нехай х – перше число, тоді у – друге число. Оскільки їх сума дорівнює 100, то маємо рівняння: х + у = 100.

За другою умовою здачі маємо рівняння: х – у = 26.

Складемо систему рівнянь:

    та розв’яжемо способом додавання

2х = 126

х = 63

у = 37

Відповідь: перше число 63, друге – 37.

Пригадаємо, з якими видами задач ми зустрічалися на початку 7 класу.

  

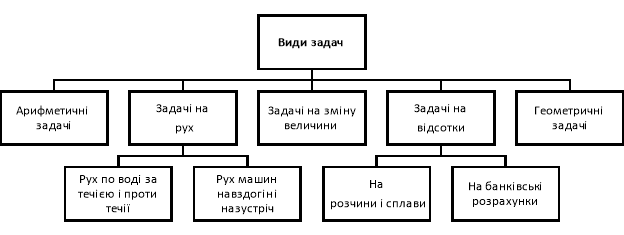
Багато задач, у яких потрібно знайти дві величини, можна розв’язати складанням рівняння з однією змінною. Однак їх зручніше  розв’язувати за допомогою системи рівнянь.

При цьому способи дій майже не відрізняються від тих способів, що були нами використані під час розв’язування текстових задач на складання рівняння з однією змінною. Тобто й види задач (арифметичні, на рух, на зміну величин та на вартість товару), і послідовність дій залишаються майже такими самими — тільки додається позначення ще однієї невідомої величини й складання та розв’язування системи двох рівнянь вивченими способами.

Розв’язуючи задачу за допомогою системи рівнянь,  слід дотримуватися такої послідовності дій:

1. позначити деякі дві невідомі величини змінними (наприклад, х і у);
2. за умовою задачі скласти систему рівнянь;
3. розв’язати одержану систему;
4. проаналізувати знайдені значення змінних відповідно до умову задачі, дати відповідь на запитання задачі;
5. записати відповідь.

7. Осмислення нового матеріалу

Робота біля дошки

№ 1079. У легкоатлетичній секції тренуються 32 спортсмени, причому дівчат серед них на 4 більше, ніж хлопців. Скільки дівчат і скільки хлопців тренується в цій секції?

Розв’язання. Нехай х – дівчат, тоді у – хлопців. Оскільки їх сума дорівнює 32, то маємо рівняння: х + у = 32.

За другою умовою здачі маємо рівняння: х – у = 4.

Складемо систему рівнянь:

    та розв’яжемо способом додавання

2х = 36

х = 18 (дівчат)

у = 18-4=12 (хлопців)

Відповідь: 18 дівчат, 12 хлобців.

№ 1081. За олівець і три зошити заплатили 8,8 грн., а за три олівці і зошит - 7,2 грн. Скільки коштує один олівець і скільки один зошит?

Розв’язання. Нехай олівець коштує х грн.,  а зошит у грн. Оскільки за олівець і три зошити заплатили 8,8 грн., то маємо рівняння: х + 3у = 8,8

За другою умовою здачі маємо рівняння: 3х+у=7,2.

Складемо систему рівнянь:

  

 та розв’яжемо способом додавання

-8y = -19,2

y=2,4 грн. - зошит,

х+32,4 = 8,8

х=1,6 грн. – олівець.

Відповідь: 2,4 грн. ; 1,6 грн..

№1083. У касі крамниці після переобліку залишилося 12 монет по 25 і 50 копійок, усього на суму 4 гривні. Скільки монет по 25 копійок і скільки по 50 копійок залишилося в касі?

Розв’язання. Нехай монет по 25 коп. було х шт.,  а по 50 коп. -  у. Оскільки у касі крамниці після переобліку залишилося 12 монет по 25 і 50 копійок, то маємо рівняння:  х + у = 12

За другою умовою здачі маємо рівняння: 0,25х+0,5у=4.

Складемо систему рівнянь:

  

    та розв’яжемо способом додавання

-y = -4

y=4 (шт.) по 50 коп.

х+у=12+х=8 (шт.) по 25 коп.

Відповідь: 8, 4.

№ 1087.Основа рівнобедреного трикутника на 2 см більша за його бічну сторону. Знайдіть сторони трикутника, якщо його периметр дорівнює 26 см.

Розв’язання. Нехай основа трикутника х см.,  а бічна -  у грн.. Оскільки периметр трикутника дорівнює 26 см, то маємо рівняння:  х + 2у = 26.

За другою умовою здачі маємо рівняння: х-у=2.

Складемо систему рівнянь:

  

    та розв’яжемо способом додавання

3y = 24

y=8 (см.) –бічна сторона рикутника,

х-у=10 (см.) – основа трикутника.

Відповідь: 8 см., 10 см.

 

V. Підсумок уроку

Якої послідовності дій слід дотримуватися, розв’язуючи задачу за допомогою системи рівнянь? ( позначити деякі дві невідомі величини змінними (наприклад, х і у); за умовою задачі скласти систему рівнянь; розв’язати одержану систему; проаналізувати знайдені значення змінних відповідно до умову задачі, дати відповідь на запитання задачі; записати відповідь.)

VI. Домашнє завдання. Оцінювання та мотивація

Опрацювати § 30, №1080.