Додаток до аналітична геометрія Планування

Додаток

Задача 1.

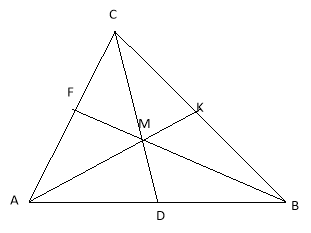Знайти координати точки перетину медіан трикутника, якщо відомі координати його вершин.

Розв’язання

Нехай маємо ∆АВС з вершинами А, В, С. АК, ВF і CD – медіани трикутника, а точка М – точка їх перетину. Знайдемо координати точки Dсередини відрізка

АВ:, . (1)

Точка М, у якій перетинаються медіани трикутника, ділить відрізок СD у відношенні 2:1, рахуючи від точки С, тому .

Координати точки М обчислюємо за відомими формулами: , ;

Підставимо в рівності (1)

.

Аналогічно: .

Координати точки перетину медіан трикутника є середнім арифметичним відповідних координат його вершин.

Точка перетину медіан трикутника є центром його маси.

Задача 2.

Загальне рівняння прямої записати в нормальному вигляді.

Розв’язання

Щоб звести загальне рівняння прямої до нормального вигляду. Треба обидві його частини помножити на нормуючий множникM=.

Знак нормуючого множника береться протилежним до знака вільного члена в загальному рівняння прямої. У нас вільний член +12, тому координуючий множник беремо зі знаком  мінус. В нас А=3, В=-3, звідси

M=.

Помножимо обидві частини рівняння на . Приведемо рівняння до нормального вигляду:

Слід пам’ятати, що в нормальному рівнянні прямої сума квадратів коефіцієнтів при х і у дорівнює 1, а вільний член має бути від’ємним.

Задача 3.

Написати параметричне рівняння прямої, яка проходить через точки А(-3;2) і В (4;-8).

Розв’язання

Запишемо канонічне рівняння прямої ;

Підставимо координати точок А і В у дане рівняння.

   ,

 Вектор називають направляючим вектором прямої.

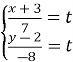Нехай ,  тоді

Тоді

Дана система задає параметричне рівняння прямої (t – параметр).

Коли точка М рухається по прямій, то параметр t змінюється за абсолютною величиною і знаком.

Якщо t – час, то параметричні рівняння визначають закон руху матеріальної точки по прямій лінії з постійною швидкістю , тобто рух відбувається за інерцією.

В нашій задачі .

Задача 4.

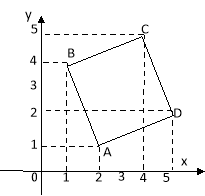
Дано протилежні вершини квадрата ABCDA (2;1) iC (4;5). Знайти координати решти вершин.

Розв’язання 

Нехай координати  точок В і D будуть B, D.

Знайдемо кутові коефіцієнти прямих

АВ і ВС

; ;

Оскільки прямі перпендикулярні, то .

(1)

Знайдемо . У квадрата .

.

Після перетворень, одержимо , а

Виконаємо підстановку у рівняння (1)

Після перетворень, одержимо

тоді .

Отже точка В має координати (5;2) або (1;4).

Якщо аналогічні міркування виконати відносно точки D то її координати будуть (5;2) або (1;4).

Зберігаючи обхід вершин квадрата (див. рис.) маємо: В (1;4), D(5;2).

Задача 5.

Звести до канонічного вигляду рівняння лінії

Розв’язання

Виділимо квадрати двочленів

Введемо заміну: , , тоді

Це є рівняння гіперболи.

Задача 6.

Які координати буде мати точка А ( при повороті системи координат на кут +60°.

Розв’язання

Координати точки в новій системі координат шукають за формулами:

, .

. , .

Маємо

; ;

; .

Задача 7.

Звести до канонічного вигляду рівняння кривої

і побудувати її графік.

Розв’язання

Оскільки в рівняння входить додаток 4ху (добуток змінних х і у) то спочатку виконаємо поворот координатних осей за формулами:

і  .

Підставимо у рівняння

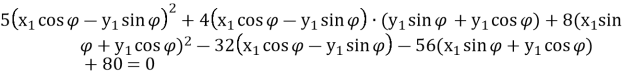
Розкрити дужки і, звівши подібні доданки, одержимо рівняння

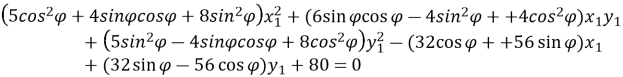(1)

Знайдемо такий кут повороту, при якому коефіцієнт при х₁у₁ буде дорівнювати нулю.

Перейдемо до рівняння

, .

Оскільки і , то осі нової системи координат взаємно перпендикулярні.

, тому кут повороту розміщений в І-й або ІІІ-й чвертях. , тому кут повороту розміщений у ІІ-й і ІV-й чвертях.

Для зручності .

Знайдемо по відомих формулах ,

. Маємо , , тоді , .

При даних коефіцієнти у рівнянні (1) будуть:

при , при х₁у₁ – (0), при , при х₁  - , при у₁ - .

Підставивши ці числа у рівняння і перетворивши його одержимо рівняння

9.

Виділивши повні квадрати одержимо .

Введемо заміну ; .

Одержимо 9, тоді .

Маємо рівняння еліпса.

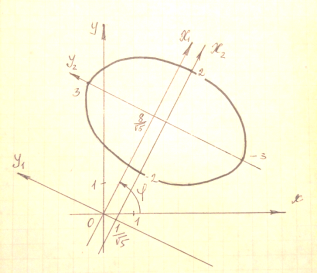
План побудови.

1.                   Виконуємо поворот системи 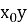на кут 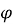. Маємо систему .
2.                   Виконуємо паралельне перенесення системи за формулами

; .

3.                   В системі 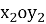будуємо еліпс.

Задача 8.

Написати канонічне і параметричне рівняння прямої, яка проходить через точку М₀ (7; -9; 8) паралельної вектору (4; 3; -2).

Розв’язання

Загальний вигляд канонічного рівняння прямої , де направляючий вектор прямої.

Маємо: ; якщо , 

то

Задача 9.

Написати рівняння площини, яка проходить через три точки М₁ (1;2;-1),

 М₂ (-1;0;4); М₃ (-2;-1;1).

Розв’язання

Підставимо координати точок у загальне рівняння площини

.

Одержимо систему:

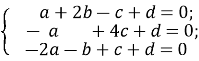
Перше додамо до другого. Потім помножимо на (+2) перше рівняння і додамо до третього. Одержимо:

Друге рівняння помножимо на 3 і додамо до першого.

.

Підставимо у перше рівняння системи:

Значення підставимо у 1-е рівняння системи (1).

Значення підставимо у загальне рівняння площини.

| :d

x-y+1=0 – шукане рівняння площини. Ця площина паралельна осі Oz.

Задача 10.

Обчислити кут між двома площинами:

i

Розв’язання

Запишемо нормальні вектори площин: ,

;

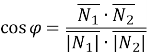
Задача 11.

Знайти точку перетину прямої і площини

Розв’язання

Запишемо рівняння прямої у параметричному вигляді

.

Підставимо значення x, yiz у рівняння площини

Значить координати шуканої точки будуть: x=1; y=2;z=2.

Задача 12.

Привести рівняння прямої до канонічного вигляду:

Розв’язання

Помножимо перше рівняння системи на 4 і додамо до другого:

(1)

Якщо х=0, то z=1. Ці дані підставимо у 1-у рівняння. Одержимо:

     у=2. М₁ (0;2;1)

Якщо у рівнянні (1) замість х поставити 11, то z=-12. Знову підставимо у 1-е рівняння системи , у= -15. М₂(11; -15; - 12)

Шукана пряма проходить через точки М₁ і М₂

або .

Задача 13.

Знайти кут між прямою і площиною
 

Розв’язання

Знайдемо косинус кута між нормальним вектором площини і направляючим вектором прямої

;

;

, тому