Дослідження "Теорія зв'язаних маятників"
1
Дослідження на тему:
ТЕОРІЯ ЗВ’ЯЗАНИХ МАЯТНИКІВ
Тези
науково-дослідницької роботи на тему:
«Теорія зв’язаних маятників»
З коливаннями ми зустрічаємось у живій природі: биття серця, рух голосових зв’язок тощо. Коливаннями називаються фізичні процеси, які точно або наближено повторюються через рівні інтервали часу. У залежності від фізичної природи розрізняють механічні й електромагнітні коливання. Підвісимо тягарець на нитці (пружині) (отримаємо маятник), відведемо його в бік від положення рівноваги й відпустимо. Тягарець почне здійснювати коливання біля положення рівноваги, тобто здійснювати періодичний рух. Більш складніший процес спостерігається при коливанні зв’язаних маятників. Це і обумовлює актуальність даної роботи.
Мета дослідження: аналізувати наукову літературу з історії дослідження маятників, підручники і посібники з вивчення маятників і зокрема, зв’язаних маятників, а також розглянути можливості вдосконалення експериментів зі зв’язаними маятниками.
Серед основних завдань дослідження були аналіз і систематизація матеріалу про історію вивчення маятників, їх параметрів; аналіз теоретичного матеріалу щодо поняття «зв’язані маятники» та розгляд можливостей вдосконалення експериментів зі зв’язаними маятниками.
Світ маятників є безмежним. Всі знання, дані про їх параметри та історію розвитку вчень не можливо вмістити у межі даної наукової роботи. Тож було акцентовано увагу на основних відомостях про маятники. Проаналізовано історію розвитку вчення про маятники, оцінено вагомий вклад у неї Галілео Галілея та Христіана Гюйгенса. У окремому розділі роботи розглянуто зв’язані маятники.
ЗМІСТ
ВСТУП 4
РОЗДІЛ 1. МАЯТНИКИ 5
1.1. Основні відомості про маятники 5
1.2. Історія вивчення маятників 8
РОЗДІЛ 2. ЗВ’ЯЗАНІ МАЯТНИКИ 14
2.1. Поняття про зв’язані маятники 14
2.2. Вдосконалення експериментів зі зв’язаними маятниками 16
ВИСНОВКИ 24
СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ 25
ВСТУП
Актуальність дослідження. Коливаються дерева у лісі, пшениця у полі, струни музичних інструментів, мембрани телефону, кузова автомобіля, поршень двигуна. Коливальні рухи відбуваються й у житті нашої планети (землетруси, припливи й відпливи). З коливаннями ми зустрічаємось і у живій природі: биття серця, рух голосових зв’язок тощо. Коливаннями називаються фізичні процеси, які точно або наближено повторюються через рівні інтервали часу. У залежності від фізичної природи розрізняють механічні й електромагнітні коливання. Наприклад, підвісимо тягарець на нитці (пружині) (отримаємо маятник), відведемо його у бік від положення рівноваги й відпустимо. Тягарець почне здійснювати коливання біля положення рівноваги, тобто здійснювати періодичний рух. Більш складніший процес спостерігається при коливанні зв’язаних маятників.
Об’єкт дослідження: процес коливання маятників, вдосконалення способів вимірювання при виконанні фізичного експерименту зі зв’язаними маятниками.
Предмет дослідження: зв’язані маятники та їх параметри.
Мета дослідження: аналізувати наукову літературу з історії дослідження маятників, підручники і посібники з вивчення маятників, а також розглянути можливість вдосконалення експериментів зі зв’язаними маятниками.
Основні завдання дослідження: аналіз і систематизація матеріалу про історію вивчення маятників; аналіз теоретичного матеріалу щодо поняття «зв’язані маятники» та розгляд можливостей вдосконалення експериментів зі зв’язаними маятниками.
Методи дослідження: аналітичний, кількісний, емпіричний, історичний та графічний.
Наукова новизна дослідження: полягає в тому, що нами зроблена спроба систематизувати існуючі матеріали про історію дослідження маятників, а також розглянути можливості вдосконалення експериментів зі зв’язаними маятниками.
Практичне значення. Ця робота може бути використана для більш поглибленого вивчення зв’язаних маятників та історії дослідження маятників при позакласному вивченні фізики.
РОЗДІЛ 1
МАЯТНИКИ
1.1. Основні відомості про маятники
Маятник - це тіло, свобода руху якого у полі тяжіння обмежена підвісом в одній точці. Маятник може здійснювати коливальні й обертальні рухи.
Маятник характеризується періодом коливань (часом, необхідним для здійснення одного повного коливального руху), частотою (кількість повних коливань, що їх здійснює тіло за одиницю часу) і амплітудою - найбільшим кутом відхилення маятника від положення рівноваги. Траєкторія руху тіла - це дуга кола, центр якого знаходиться у точці підвісу, а радіус дорівнює відстані від точки підвісу до центру кульки. Рух тіла від крайнього правого положення до крайнього лівого і назад називають одним повним коливанням. Далі усе повториться спочатку. Якщо спостерігати за тілом достатньо довго, то ми помітимо, що віддалі, на які воно відхиляється вліво і вправо, поступово зменшуються. Причиною цього є сили тертя. Врешті-решт коливання припиняться.
Коливання маятника були б неможливі, якби не було сили земного тяжіння. Тому Земля (або інша планета на якій знаходиться маятник) є невід’ємною складовою частиною коливальної системи, яку ми називаємо маятником.
Для дослідження явищ, які відбуваються за участю різних тіл, але мають спільні риси, широко використовують моделі. Досліджуючи рух тіл, розмірами яких за певних умов можна знехтувати, ми замінювали їх моделлю – матеріальною точкою. Розглядаючи автомобіль, потяг, планету як матеріальну точку, простіше виділити й описати особливості їх рухів. Щоб виявити загальні властивості коливань і спростити їх вивчення, реальні тіла, які коливаються, теж замінюють їх моделлю. У фізиці розглядаються спрощені моделі реального маятника: математичний і фізичний маятники [6, с. 177].
Математичний маятник - це матеріальна точка (практично тіло малих розмірів), що підвішена на невагомому нерозтяжному стрижні до нерухомої точки, яка здійснює під впливом сили тяжіння коливання по дузі кола. У моделі математичного маятника коливання здійснюються на площині. Час за який маятник здійснить одне повне коливання (повернеться в початковий стан) називається періодом коливань. Період коливань математичного маятника визначається за формулою:
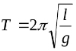 ,
,
де l - довжина математичного маятника, g - прискорення вільного падіння.
Період коливань математичного маятника залежить лише від прискорення вільного падіння у даному місці Землі і від довжини маятника. Період математичного маятника не залежить від амплітуди коливань і від маси підвішеного тягарця, що легко перевірити на дослідах з різними маятниками. Слід лише пам’ятати, що розміри тягарця мають бути малими порівняно з довжиною підвісу і малим має бути також кут відхилення маятника від вертикалі [1, с. 206].
Прискорення вільного падіння в різних місцях земної поверхні на одній і тій самій географічній широті є неоднаковими і залежить, хоча й незначно, від густини порід, з яких складаються верхні шари земної кори. Наприклад, у районі Кривого Рогу, де залягають залізні руди, прискорення вільного падіння дещо більше за середнє значення для цієї широти. Навпаки, в районах газових і нафтових родовищ прискорення вільного падіння виявляється дещо меншим за середнє для цієї широти. Тому за результатами вимірювань прискорення вільного падіння можна виявити райони залягання корисних копалин - залізної руди, нафти, газу тощо. Оскільки прискорення вільного падіння на різних планетах є різним, то й період коливань математичного маятника є неоднаковим [2, с. 114].
Математичні маятники використовують для регулювання ходу годинників, оскільки будь-який маятник має цілком певний період коливань, застосовуються у багатьох галузях машинобудування, в геологічній розвідці [10, с. 167].
Фізичний маятник - це матеріальна точка (вантаж), закріплена в одній точці, яка не є його центром інерції, на нерухомій горизонтальній осі, навколо якої вона може під дією сили тяжіння здійснювати коливальні рухи. Період коливань фізичного маятника визначається за формулою:
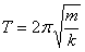 ,
,
де m - маса матеріальної точки, k - коефіцієнт пружності пружини (постійна величина для пружини, що характеризує її пружні властивості).
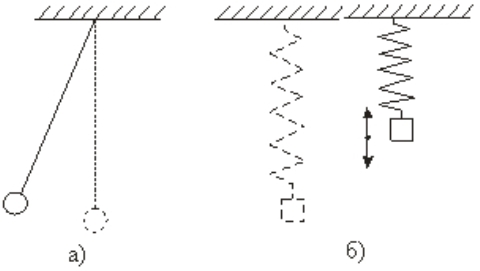
|
Рис. 1.1. Маятники: математичний (а) та фізичний (б) |
На відміну від простих моделей рух реального маятника складний. Крім коливань в одній площині, підвішене на нитці тіло може здійснювати також колові рухи. Крім того, воно може крутитися навколо власної осі (крутильний маятник) [1, с. 201].
Механічними коливаннями називаються періодичні зміни положення тіла (системи тіл), при яких воно неодноразово повертається в початковий стан. Коливання поділяються на вільні і вимушені. Математичний та фізичний (пружинний) маятники здійснюють вільні коливання.
1.2. Історія вивчення маятників
|
Рис. 1.2. Галілео Галілей |
 Аналіз науково-методичної літератури дозволив виокремити кілька праць, у яких розглядається історія становлення вчення про маятники та їх застосування. Михайло Дудик та Юлія Дегтяренко відзначили вагомий вклад у побудові фізичної картини, вивченням маятників займався італійський мислитель епохи Відродження Галілео Галілей. Уже в студентські роки він зробив відкриття великої наукової і практичної важливості – відкрив закон ізохронності коливань маятника. За розповіддю італійського математика і фізика Вінченцо Вівіані, відкриття закону сталося при таких обставинах: «завдяки гострому розуму Галілео винайшов простий і правильний спосіб вимірювання часу з допомогою маятника, ніким до нього непередбачений. Для цього скористався випадковим спостереженням коливань люстри, коли був у Пізанському соборі, зробив точний дослід, переконався в рівній тривалості коливань, і йому тоді ж спало на думку пристосувати маятник до медицини для вимірювання биття пульсу, на диво і захоплення лікарів, і в тому вигляді, як це і тепер вживається. Цим відкриттям він потім користувався у багатьох дослідах для вимірювання часу і рухів і першим застосував його до спостереження небесних тіл, чим досягнув вагомих результатів в астрономії і географії» [4, с. 40].
Аналіз науково-методичної літератури дозволив виокремити кілька праць, у яких розглядається історія становлення вчення про маятники та їх застосування. Михайло Дудик та Юлія Дегтяренко відзначили вагомий вклад у побудові фізичної картини, вивченням маятників займався італійський мислитель епохи Відродження Галілео Галілей. Уже в студентські роки він зробив відкриття великої наукової і практичної важливості – відкрив закон ізохронності коливань маятника. За розповіддю італійського математика і фізика Вінченцо Вівіані, відкриття закону сталося при таких обставинах: «завдяки гострому розуму Галілео винайшов простий і правильний спосіб вимірювання часу з допомогою маятника, ніким до нього непередбачений. Для цього скористався випадковим спостереженням коливань люстри, коли був у Пізанському соборі, зробив точний дослід, переконався в рівній тривалості коливань, і йому тоді ж спало на думку пристосувати маятник до медицини для вимірювання биття пульсу, на диво і захоплення лікарів, і в тому вигляді, як це і тепер вживається. Цим відкриттям він потім користувався у багатьох дослідах для вимірювання часу і рухів і першим застосував його до спостереження небесних тіл, чим досягнув вагомих результатів в астрономії і географії» [4, с. 40].
Можна припустити, що Галілей неодноразово міркував над тим, як застосувати маятник для створення точного годинника, але до розробки механізму приступив лише у віці більше 70-ти років, – вже після того як осліп. За вказівками Галілея розробку годинника продовжили його син Вінченцо і учень Вівіані, але невідомо, чи вдалося їм виготовити годинник – залишилися лише креслення, на основі яких згодом виготовили модель годинника.
|
Рис. 1.3. Христіан Гюйгенс |
 У галузі механіки основна увага в XVII столітті була звернена на розробку таких трьох питань, як маятник, удар, тяжіння. Питання про маятник пов'язане з ім'ям нідерландського вченого-механіка, математика і фізика - Xристіана Гюйгенса (1629-1695), який в 1658 році у праці «Маятникові годинники» описав сконструйований ним перший маятниковий годинник. Це було важливим відкриттям конструктивно-технічного напрямку періо-ду мануфактур [7, с. 101].
У галузі механіки основна увага в XVII столітті була звернена на розробку таких трьох питань, як маятник, удар, тяжіння. Питання про маятник пов'язане з ім'ям нідерландського вченого-механіка, математика і фізика - Xристіана Гюйгенса (1629-1695), який в 1658 році у праці «Маятникові годинники» описав сконструйований ним перший маятниковий годинник. Це було важливим відкриттям конструктивно-технічного напрямку періо-ду мануфактур [7, с. 101].
Христіану Гюйгенсу також належить ідея про те, що за допомогою маятника можна вимірювати прискорення вільного падіння g [4, с. 54-55].
Розвиток теорії механіки від Галілея до Гюйгенса було сконцентровано у теорії маятника та пружного і непружного удару. Рух маятника вивчали і вчені інших епох. Зокрема, італійський вчений часів Наукової революції XVII століття Джованні Бореллі розвивав учення Галілео Галілея про маятник (у 1663 році Галілео Галілей з’єднав маятник з лічильником і запропонував проект годинника і довів, що прискорення і сповільнення маятника викликають одні і ті ж причини – його тяжіння). Христіан Гюйгенс показав, що коливання будь-якого тіла може бути зведено до простого маятника й описуватись математичним апаратом розробленим для маятника. На цій основі Христіан Гюйгенс розробив класичну теорію руху маятника. Годинник з маятником став основою для точної експериментальної техніки. Стався історичний перехід від геометричних форм і траєкторій тіл, що рухаються, до дійсно фізичних задач [7, с. 114].
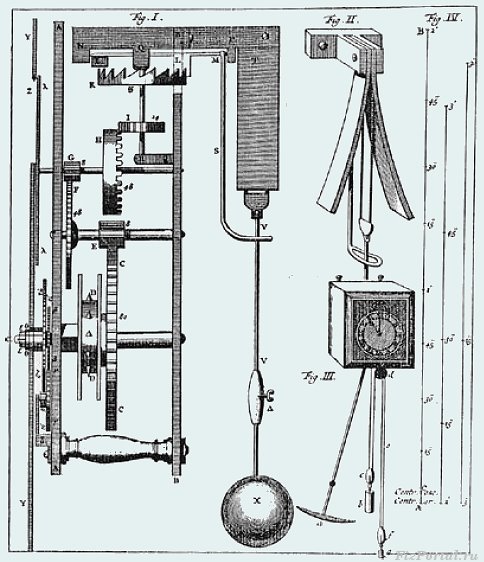
|
Рис. 1.4. Маятниковий годинник Гюйгенса |
Перший годинник з циклоїдальним маятником за проектом Гюйгенса виготовив майстер С.Костер. Такий годинник мав похибку 5-10 секунд за добу. У 1675 році Христіан Гюйгенс одночасно з Робертом Гуком запропонував використовувати як регулятор коливань систему «баланс-спіраль», яка складається з колеса з масивним металевим ободом, закріпленим на вісі, і тонкої пружини, один кінець якої кріпиться до осі балансу, а другий - до нерухомої опори. Ця система виявилася надто чутливою до зміни температури, бо при зміні температури змінювалась не лише довжина пружини, а й її пружні властивості. Неможливість добитися стабільного ходу годинника з великою амплітудою коливань маятника, яка необхідна для роботи шпиндельного механізму, змусила майстрів шукати засоби використання коливань з малою амплітудою. Таким засобом став анкерний механізм. У ньому зубці анкера (Anker - німецькою означає якір), який знаходиться на осі маятника, по черзі входять у зчеплення з зубцями ходової шестерні і регулюють її обертання. Перший годинник з анкерним механізмом виготовив у 1671 році англієць Вільям Клемент (1640-1696). Анкерний механізм вдосконалив у 1715 році англієць Джордж Ґрехем (1673-1751), який винайшов невільний анкерний механізм, що має значно менші втрати енергії, ніж механізм Клемента. Використавши цей механізм, Ґрехем створив годинник з точністю ходу 0,1 секунди. Механізм Джорджа Ґрехема застосовували в астрономічних обсерваторіях до 1890 року - майже 200 років. Він кілька років досліджував вплив різних факторів на хід годинника і дійшов висновку, що вирішальну роль має зміна температури. Визначивши коефіцієнти температурного розширення різних металів, Ґрехем винайшов ртутний компенсаційний маятник. Маятник був наповнений ртуттю, яка має коефіцієнт теплового розширення на порядок вищий, ніж залізо. При підвищенні температури довжина маятника зростає. Водночас ртуть піднімається у трубці і компенсує опускання центру ваги маятника. Одночасно з Ґрехемом над проблемою температурної компенсації маятника працював Джон Гаррісон (1693-1776). У 1726 році він сконструював решітчастий маятник із поздовжніх залізних і поперечних латунних стержнів. При підвищенні температури через розширення залізних стержнів довжина маятника зростала. Але латунні стержні, розширюючись, викривляли стальні стержні, компенсуючи зростання довжини маятника.
Бенджамін Робінс (1707-1771) у праці «Нові принципи артилерії» виклав результати дослідження опору середовища рухові снаряда, тобто займався питаннями зовнішньої балістики. Оскільки цей опір в усякому разі є функцією швидкості, то Робінс розробив методику визначення швидкості снаряда в будь-якій точці шляху. Для цієї мети він сконструював балістичний маятник [4, с. 78].
Коливання фізичного маятника розглядали X. Гюйгенс, Я. Бернуллі, і Л. Ейлер. Однак спільне рішення задачі про знаходження динамічних реакцій зв'язків невільною матеріальної системи було дано вперше ученим і філософом Ж. Даламбером (1717-1783 роки). Характеризуючи роботи своїх попередників, він пише «Я обмежуся тут розглядом руху ... тих тіл, які тягнуть один одного за допомогою ниток або жорстких стержнів. Я охоче зупиняюся на цьому питанні, бо до сих пір (1742 рік) тільки невелика кількість завдань цього роду розглядається найбільшими математиками». Коливання зв’язаних маятників досліджували Х. Гюйгенс, О. Майер, М. Баутін.
|
Рис. 1.5. Маятник Фуко у КПІ |
 У 1851 році Леон Фуко створив прилад, який отримав назву «Маятник Фуко». Він використовується для демонстрації обертання Землі навколо своєї осі. Вперше демонстрація маятника Фуко відбулася у Парижі. Маятник Фуко - це великий масивний маятник зі значним періодом коливання, підвішений до склепіння просторої високої зали. На підлозі під маятником зазвичай малюють коло з поділками, щоб відслідковувати зміну площини коливання відносно поверхні Землі. Згідно із законом збереження моменту імпульсу коливання маятника відбуваються зі збереженням площини коливання. Водночас внаслідок обертання Землі, орієнтація цієї площини відносно приміщення змінюється, у чому можна переконатися, спостерігаючи за маятником протягом певного часу. Період обертання площини коливань
У 1851 році Леон Фуко створив прилад, який отримав назву «Маятник Фуко». Він використовується для демонстрації обертання Землі навколо своєї осі. Вперше демонстрація маятника Фуко відбулася у Парижі. Маятник Фуко - це великий масивний маятник зі значним періодом коливання, підвішений до склепіння просторої високої зали. На підлозі під маятником зазвичай малюють коло з поділками, щоб відслідковувати зміну площини коливання відносно поверхні Землі. Згідно із законом збереження моменту імпульсу коливання маятника відбуваються зі збереженням площини коливання. Водночас внаслідок обертання Землі, орієнтація цієї площини відносно приміщення змінюється, у чому можна переконатися, спостерігаючи за маятником протягом певного часу. Період обертання площини коливань
маятника Фуко залежить від широти.
Маятники Фуко на території України є у музеї пізнання світогляду та освоєння космосу (Переяслав-Хмельницький), бібліотеці Київського політехнічного інституту (Київ), Харківському національному університеті і харківському планетарії (Харків), Ужгородському національному університет, церкві Пресвятої Євхаристії (Львів), Національному педагогічному університеті імені М. П. Драгоманова (Київ) та СРК «Adrenalin City» (Луцьк).
Відзначимо, що нині механічні маятникові годинники (були основним «двигуном» для розвитку теорії маятників) стали екзотикою. Проблеми їх удосконалення давно перестали бути темами дисертацій чи наукових конференцій. А їх історія сприймається як казка - цікаво, повчально, але дуже далеко від сучасного життя. Перші механічні годинники, баштові, були споруджені ще у XIV столітті. До XVI століття вони мали лише одну стрілку - годинну. Їхній механізм рухали гирі, що опускалися, а хід регулювався шпиндельним механізмом. Цей механізм включав коронну шестерню, яка оберталась навколо горизонтальної осі, вертикально розташований шпиндель (стержень з двома лопатками, розташованими приблизно під кутом 90 градусів) і приєднаний до шпинделя горизонтальний балансир – стержень з розміщеними на ньому вантажами, які можна було переміщувати, щоб регулювати хід годинника. Коли шестерня оберталась, лопатки отримували поштовхи від зубців, в одну чи другу сторону, внаслідок чого балансир здійснював коливання, якими визначався хід годинника. Період коливань залежав від моменту інерції системи шпиндель-балансир, сили поштовхів і тертя. Ці фактори важко було стабілізувати. Зокрема, момент інерції балансира внаслідок його теплового розширення або стиснення змінювався навіть протягом доби. Через це шпиндельні годинники мали низьку точність – не вище ніж півгодини на добу і їх підводили за сонцем.
РОЗДІЛ 2
ЗВ’ЯЗАНІ МАЯТНИКИ
2.1. Поняття про зв’язані маятники
Як відомо, коливанням називається всякий рух або зміна стану тіла (коливальної системи), що характеризується тим чи іншим ступенем повторюваності в часі значень фізичних величин, які визначають цей рух або стан тіла. Вільні коливання коливальної системи відбуваються після того, як вона була виведена із стану рівноваги і залишена сама на себе. Власні коливання системи здійснюються за рахунок енергії, яка була надана системі і відбуваються за відсутності дії в цій системі сил опору, а також за відсутності дії на неї інших зовнішніх впливів.
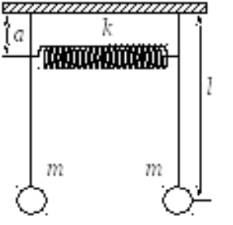
|
Рис. 2.1. Зв’язані маятники |
 Коливання називаються періодичними, якщо значення фізичних величин, які змінюються в процесі коливань, повторюються через однакові проміжки часу. Найпростішим типом періодичних коливань є так звані гармонічні коливання, при яких значення фізичної величини змінюються у часі за законом косинуса (синуса). Якщо абсолютно тверде тіло (фізичний маятник) здійснює малі власні вільні гармонічні коливання, то його період коливань не залежить від амплітуди коливань (ізохронність маятника). При цьому тіло коливається з власною частотою коливань, яка визначається параметрами даної коливальної системи.
Коливання називаються періодичними, якщо значення фізичних величин, які змінюються в процесі коливань, повторюються через однакові проміжки часу. Найпростішим типом періодичних коливань є так звані гармонічні коливання, при яких значення фізичної величини змінюються у часі за законом косинуса (синуса). Якщо абсолютно тверде тіло (фізичний маятник) здійснює малі власні вільні гармонічні коливання, то його період коливань не залежить від амплітуди коливань (ізохронність маятника). При цьому тіло коливається з власною частотою коливань, яка визначається параметрами даної коливальної системи.
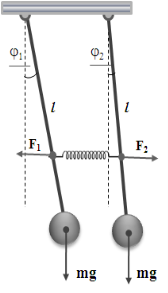
Кожне з двох твердих тіл, зв’язаних одне з одним динамічним зв’язком, які утворюють, так звану зв’язану систему, буде коливатися з двома різними частотами. Властивості будь якої зв’язаної системи визначаються властивостями двох вихідних коливальних систем, які утворюють цю зв’язану систему. Якщо різниця частот коливань мала, то будуть спостерігатися биття, тобто періодична зміна (збільшення і зменшення) амплітуди коливань.
Два математичних маятники, з’єднані між собою пружиною, є найпростішим прикладом зв’язаної системи. Маятники мають однакові власні частоти коливань, доки коливаються незалежно один від одного. Частота довільних коливань маятника за наявності зв’язку відрізняється від його власної частоти, оскільки при коливанні маятників пружина деформується і, значить, змінюється сила, яка діє на маятники. При відхиленні одного з маятників з положення рівноваги за наявності динамічного зв’язку між маятниками буде відхилятись і другий маятник.
Розглянемо на якісному рівні особливості коливання двох однакових маятників, зв’язаних пружиною (рис. 2.1). Відхилимо подумки один з них (правий) на певний кут від положення рівноваги так, щоб пружина здеформувалась. Лівий маятник при цьому повинен перебувати у стані спокою. Потім правий маятник відпустимо. Він почне коливатись навколо положення рівноваги. Спочатку правий маятник гойдається так, ніби ніякого зв’язку з лівим він не має. Поступово лівий маятник також почне розгойдуватися, оскільки між маятниками почне здійснюватись обмін коливальною енергією. Так як енергія від правого маятника, буде поетапно передаватися лівому маятнику, то з часом амплітуда коливань правого маятника буде поступово зменшуватись, в той час як амплітуда коливань лівого маятника буде зростати. Все це буде тривати деякий час половини періоду биття доти, доки правий маятник не зупиниться. При цьому лівий маятник (якщо втрати на тертя малі) буде коливатись майже з такою ж амплітудою, яка була у правого маятника спочатку.
Потім маятники знову поступово «обмінюються ролями»: лівий маятник буде розгойдувати правий, а тому процес обміну коливальною енергією повністю повториться, так як маятники однакові. Таким чином обидва маятники, з’єднані між собою пружиною, будуть здійснювати коливання, амплітуди яких увесь час, то збільшуються, то зменшуються (рис. 2.2.). Як відомо, такі коливання називаються биттями, а час - періодом биття. Биття виникають в результаті складання власних (нормальних) коливань обох систем [8, с. 47-52].
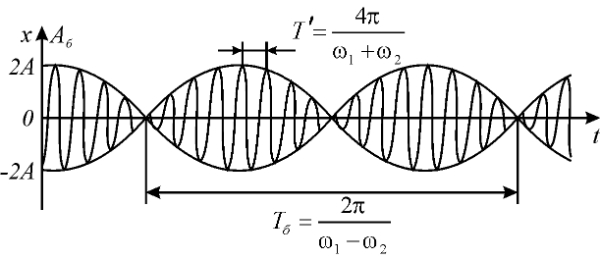
|
Рис. 2.2. Графік коливань зв’язаних маятників |
Власні коливання двох зв’язаних маятників можуть бути представлені як результат додавання (накладання, суперпозиції) двох гармонічних коливань, які здійснюються з різними циклічними частотами. Вони залежать від фізичних параметрів маятників: їх довжини, маси, коефіцієнта жорсткості пружини, відстані від місця її закріплення до вісі обертання маятника.
2.2. Вдосконалення експериментів зі зв’язаними маятниками
Проблеми, пов’язані з якістю проведення фізичних експериментів, зокрема, з дослідження зв’язаних маятників, хвилюють спільноту дослідників і нині. У наукових праць О. І. Бугайова, В. Ю. Бикова, В. П. Вовкотруба, М. В. Головка, М. І. Жалдака, О. І. Ляшенко, М. І. Садового, М. І. Шута та інших учених-дослідників розглядаються питання удосконалення шкільного фізичного експерименту [8, с. 47-48].
Так, І.В. Корсун акцентує увагу на тому, що на сьогодні дослідницький характер фізичного експерименту, як правило, віддає своє місце експерименту репродуктивному. На лабораторних роботах учні часто працюють вже із зібраними установками. За цих умов їм залишається лише за детально розробленою інструкцією натискати кнопки [5, с. 132]. При виконанні експерименту зі зв’язаними маятниками наявні суттєві похибки вимірювання. Для їх зменшення варто вдосконалювати фізичне обладнання. В останні роки впроваджується в країнах колишнього Радянського Союзу обладнання німецького виробництва «PHYWE».
За допомогою вищезазначеного новітнього обладнання вдосконалено лабораторну роботу «Вивчення коливань зв’язаних маятників з використанням установки «Кобра 3».
У цій роботі використовувалося наступне обладнання: інтерфейс «Кобра 3», базовий блок, USB з програмним забезпеченням, джерело струму для інтерфейсу, рулетка довжиною 2 м, з’єднувальний провідник довжиною 1 м, маятник із записуючим пристроєм, пружина жорсткістю 3 Н/м, тримач для вантажу масою 10 г, вантаж масою 10 г, електролітичний конденсатор ємністю 10 мкФ, джерело струму 12 В, настільний затискач, стрижень для штативу із квадратним перерізом 630 мм та правий кутовий затискач [9, с. 103-105].
|
Рис. 2.3. Установка для вивчення зв’язаних маятників |
Рис. 2.4. Графічне відображення зв’язаних маятників
|
Маятник складається з двох довгих легких стержнів у верхній частині яких розміщено кріплення на підшипнику, а у нижній чечевиця маси m (рис. 2.3). Площина руху маятників співпадає з площиною рамки, яка складається з двох стержнів від універсального фізичного штативу закріплених на столі. На відстані ![]() від точки коливання в отворах горизонтально кріпиться легка пружина зв’язку. У верхній частині розміщені датчики, які реєструють кути відхилу маятників, які сполучені з комп’ютером, на якому реально відображається коливання в часі.
від точки коливання в отворах горизонтально кріпиться легка пружина зв’язку. У верхній частині розміщені датчики, які реєструють кути відхилу маятників, які сполучені з комп’ютером, на якому реально відображається коливання в часі.
Принцип роботи. Два маятника з однаковою довжиною з’єднані спіральною пружиною. Визначити залежність амплітуди затухаючих коливань обох маятників від часу при різних режимах коливань та коефіцієнти зв’язку за допомогою персонального комп’ютера та системи «Кобра 3» [9, с. 103-105]. Перед виконанням вправ вмикаємо комп’ютер і входимо в операційну систему як користувач; на робочому столі запускаємо програму «Oscill_02».
За допомогою новітнього обладнання можна виконати шість експериментальних завдань зі зв’язаними маятниками.
Вправа 1. Визначення коефіцієнта жорсткості пружини та частоти коливань маятника способом статичних вимірювань та параметрів установки.
Вправа виконується традиційним способом. На стрижні кріпимо пружину від зв’язаних маятників. На протилежному кінці пружини кріпимо вантаж масою ![]() , рис. 2.3. За допомогою міліметрової шкали лінійки вимірюємо видовження пружини
, рис. 2.3. За допомогою міліметрової шкали лінійки вимірюємо видовження пружини ![]() . Величину маси
. Величину маси ![]() та
та ![]() заносимо в таблицю. Будуємо графік
заносимо в таблицю. Будуємо графік ![]() . В межах невеликих амплітуд дана залежність є прямою залежністю. Дані заносимо в програму методу найменших квадратів, яка поміщена в комп’ютер. На моніторі висвічується графік
. В межах невеликих амплітуд дана залежність є прямою залежністю. Дані заносимо в програму методу найменших квадратів, яка поміщена в комп’ютер. На моніторі висвічується графік ![]() та значення коефіцієнта жорсткості пружини за нахилом прямої.
та значення коефіцієнта жорсткості пружини за нахилом прямої.
Вправа 2. Визначення першої та другої частин коливань зв’язних маятників.
У набір входять стрижні, з яких монтується рамка (рис. 2.3). На підшипниках кріпляться вертикально стрижні. На перший стрижень в отвір фіксуємо один кінець пружину, а другий – на іншому стрижні (рис. 2.3). Розглядаємо випадок, коли в початковий момент часу ![]() маятники відхилені в одну сторону на однаковий кут α1=α2 від положення рівноваги. Тоді зв’язані маятники коливаються синхронно з однаковою амплітудою та першою нормальною частотою
маятники відхилені в одну сторону на однаковий кут α1=α2 від положення рівноваги. Тоді зв’язані маятники коливаються синхронно з однаковою амплітудою та першою нормальною частотою 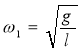 , де
, де ![]() – довжина маятника (від підвісу до вантажу,
– довжина маятника (від підвісу до вантажу, ![]() – прискорення вільного тяжіння). Пружина не розтягується і не впливає на рух маятників. Якщо маятники відхилити на однакові кути
– прискорення вільного тяжіння). Пружина не розтягується і не впливає на рух маятників. Якщо маятники відхилити на однакові кути ![]() , але в протилежні сторони, то обидва маятники будуть коливатися з другою нормальною частотою
, але в протилежні сторони, то обидва маятники будуть коливатися з другою нормальною частотою 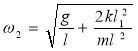 , де
, де ![]() – коефіцієнт пружності, який визначено під час виконання першої вправи,
– коефіцієнт пружності, який визначено під час виконання першої вправи, ![]() – маса маятника,
– маса маятника, ![]() – відстань між підвісом маятника та точкою кріплення пружини.
– відстань між підвісом маятника та точкою кріплення пружини.
Виміри та обчислення заносимо в таблицю. За формулами розраховуємо значення нормальних частот 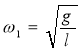 та
та 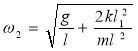 .
.
Вправа 3. Дослідження коливань зв’язних маятників графічним способом та визначення частоти коливальної системи зв’язних маятників.
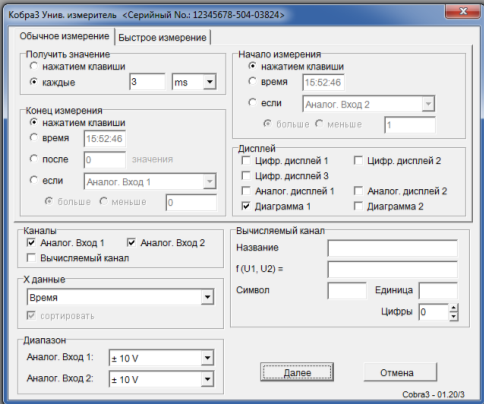
Рис. 2.5. Вікон налаштування параметрів системи «Кобра 3»
Налаштовуємо систему «Кобра 3». Після натиску кнопки «Далее» у вікні системи, що зображена на рисунку 2.5, з’являється вікно показу графіка залежності кутової частоти від часу. Щоб розпочати вимірювання, потрібно натиснути на кнопку «Почати вимірювання». Під час вимірювання вище зазначена кнопка буде неактивною, а на екрані користувачі системи отримають потрібний графік. По закінченню вимірювань натискуємо на кнопку «Закінчити вимірювання». Для збереження результатів натискаємо кнопку «Зберегти значення». Спочатку визначаємо періоди коливань кожного маятника окремо за відсутності пружини, рис. 3. Для цього лівою клавішею мишки установимо курсор у вікно «Експеримент». Відхиляємо правий маятник на невеликий кут і відпускаємо його. Внизу монітора маємо зображення коливань маятника (рис. 2.6). Лівий маятник не коливається. Відраховуємо 10-20 коливань.
![]()
![]()
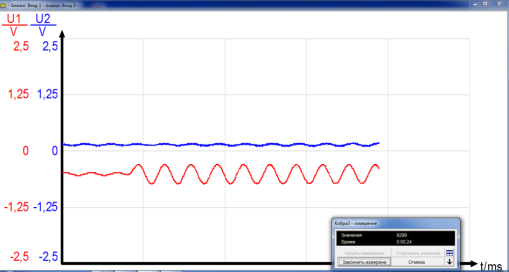
Рис. 2.6. Графік коливання правого маятника
Далі приводимо у коливання і лівий маятник і спостерігаємо крім графіка світлішого кольору правого маятника, ще й коливання лівого маятника – графік темнішого кольору (рис. 2.7). Амплітуди коливань у них різні, але частоти однакові, бо їх довжини однакові. Натискуємо на ліву клавішу мишки і підводимо курсор до вікна «Експеримент». Потім курсор перемістимо до першої межі інтервалу, що вимірюється і натискуємо на ліву клавішу мишки. Появиться вертикальна лінія, потім переміщаємося до другого часового інтервалу і появляється друга вертикальна лінія (рис. 2.7). Між цими лініями рахуємо час та кількість коливань. Дослід повторюємо декілька разів.
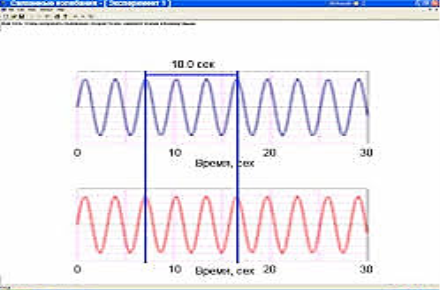
Рис. 2.7. Коливання правого та лівого маятників, які не зв’язані пружиною
Після цього досліджуємо лівий маятник, правий буде нерухомим. За результатами спостережень та вимірювань визначаємо періоди коливань обох маятників ![]() ,
, ![]() , та першу нормальну частоту
, та першу нормальну частоту ![]() . Важливо оцінити похибку. У разі різних амплітуд, має місце графік, який подано на рисунку 2.8.
. Важливо оцінити похибку. У разі різних амплітуд, має місце графік, який подано на рисунку 2.8.
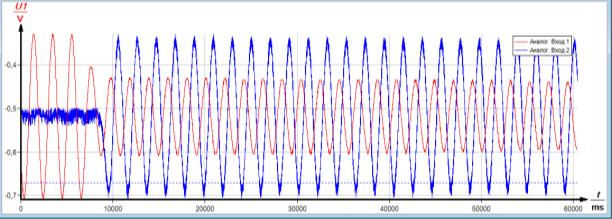
Рис. 2.8. Графіки коливання маятників різних амплітуд
Вправа 4. Визначення другої нормальної частоти коливань зв’язної системи маятників. На стрижнях маятників кріпимо пружину. Відхиляємо обидва маятники в протилежні напрямки на рівний початковий кут. Запускаємо коливання маятників. У вікні експеримент відображається коливання маятників (рис. 2.8). Здійснюємо виміри на графіках та відповідні дані заносимо в таблицю. Далі необхідно обчислити середнє значення періоду зв’язного коливання і обрахувати другу нормальну частоту ![]() . Переконуємося, що періоди обох коливань будуть однакові.
. Переконуємося, що періоди обох коливань будуть однакові.
Вправа 5. Визначення частоти биття системи зв’язних маятників.
Виконання вправи забезпечується дослідницьким шляхом. Спочатку правий маятник відхиляємо на певний кут, а другий знаходиться у стані спокою. Відпускаємо відхилений маятник. У вікні «Експеримент» відображаються коливання зв’язних маятників. Через деякий час установиться два-три періоди биття (рис. 2.9).
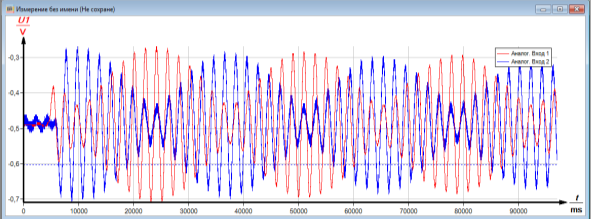
Рис. 2.9. Графік биття зв’язних маятників впродовж 9500 с
Вимірювання амплітуд та частот можна визначити виділивши вертикальними та горизонтальними лініями відповідні ділянки графіків. Значення періоду биття та стоячих хвиль заносимо у таблицю. Дослід повторюємо 3-5 разів.
Вправа 6. Дослідження графіків системи зв’язних коливань на предмет затухання.
В роботі необхідно порівняти одержані графіки биття системи зв’язних коливань впродовж тривалого часу. Для цього налаштовуємо систему «Кобра 3» і виводимо на екран монітора графіки (рис. 2.10). Звертаємо увагу на рівність частот, періодів коливань на графіках. Впродовж порівняно великого часу коливання затухають однаково за амплітудою. Крім цього по фазі графіки зміщені на ![]() . У результаті виконаних вправ виділяємо числові дані, одержані з графіків, та обрахованих із статичних вимірів й параметрів установки, порівнюємо їх і робимо висновки про їх однаковість з високою точністю. Вимірювальна система «Кобра 3» дає можливість записати графіки коливань з допомогою кольорового принтера і виконати їх вивчення на папері [9, с. 103-109].
. У результаті виконаних вправ виділяємо числові дані, одержані з графіків, та обрахованих із статичних вимірів й параметрів установки, порівнюємо їх і робимо висновки про їх однаковість з високою точністю. Вимірювальна система «Кобра 3» дає можливість записати графіки коливань з допомогою кольорового принтера і виконати їх вивчення на папері [9, с. 103-109].
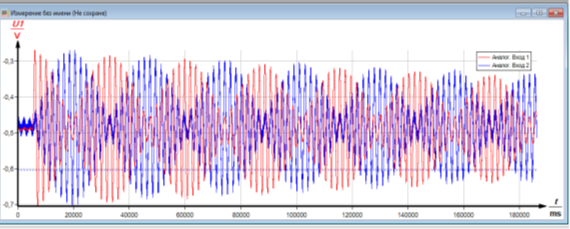
Рис. 2.10. Графік биття зв’язних маятників впродовж 18500 с
Новітнє обладнання німецького виробництва фірми «PHYWE» дає можливість безпосередньо вивчати натуральні об'єкти, розвивати практичні уміння і навички, здібності до самостійної роботи.
ВИСНОВКИ
У даному дослідженні розглянули коливання маятників і зокрема, зв’язаних маятників. Зазначимо, що коливанням називається всякий рух або зміна стану тіла (коливальної системи), що характеризується тим чи іншим ступенем повторюваності в часі значень фізичних величин, які визначають цей рух або стан тіла. Вільні коливання коливальної системи відбуваються після того, як вона була виведена із стану рівноваги і залишена сама на себе. Власні коливання системи здійснюються за рахунок енергії, яка була надана системі і відбуваються за відсутності дії в цій системі сил опору, а також за відсутності дії на неї інших зовнішніх впливів.
Коливання називаються періодичними, якщо значення фізичних величин, які змінюються в процесі коливань, повторюються через однакові проміжки часу. Найпростішим типом періодичних коливань є так звані гармонічні коливання, при яких значення фізичної величини змінюються у часі за законом косинуса (синуса). Якщо абсолютно тверде тіло (фізичний маятник) здійснює малі власні вільні гармонічні коливання, то його період коливань не залежить від амплітуди коливань (ізохронність маятника). При цьому тіло коливається з власною частотою коливань, яка визначається параметрами даної коливальної системи.
Також проаналізовано історію розвитку вчення про маятники, оцінено вагомий вклад у неї видатних мислителів Галілео Галілея та Христіана Гюйгенса.
У окремому розділі роботи розглянуто зв’язані маятники, найпростішим прикладом яких є два математичні маятники, що з’єднані між собою пружиною. Маятники мають однакові власні частоти коливань, доки коливаються незалежно один від одного. Частота довільних коливань маятника за наявності зв’язку відрізняється від його власної частоти, оскільки при коливанні маятників пружина деформується і, значить, змінюється сила, яка діє на маятники. При відхиленні одного з маятників з положення рівноваги за наявності динамічного зв’язку між маятниками буде відхилятись і другий маятник. Окрім того подано графік коливань зв’язних маятників з різними періодами та амплітудами, а також розглянуто коливань одного зі зв’язаних маятників системи.
СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ
1. Бар'яхтар В.Г. Фізика. 10 клас. Академічний рівень: [підр. для загальноосвіт. навч. закл.] / В.Г. Бар'яхтар, Ф.Я. Божинова. - X.: «Ранок», 2010. - 256 с.
2. Генденштейн Л.Е. Фізика. 10 клас: [підр. для загальноосвіт. навч. закл.] / Л.Е. Генденштейн, І.Ю. Ненашева. - X.: «Гімназія», 2010. - 272 с.
3. Даценко І.П. Зв’язані маятники: модернізація стандартного обладнання і маятник «два в одному» / І.П. Даценко, Ю.П. Мінаєв, М.А. Попович // Вісник Чернігівського національного педагогічного університету. Серія: Педагогічні науки. - 2014. - Вип. 116. - С. 23-27.
4 Дудик М.В. Історія фізики (курс лекцій): [навч. пос. для студ. вищих навч. закл.] / Укладачі: М.В. Дудик, Ю.В. Діхтяренко - Умань: ПП «Жовтий», 2015. - 192 с.
5. Корсун І.В. Вдосконалення експериментальної підготовки майбутніх учителів фізики / І.В. Корсун // Науковий часопис Національного педагогічного університету ім. М.П. Драгоманова. Серія № 5. Педагогічні науки: реалії та перспективи. - К.: НПУ імені М. П. Драгоманова, 2012. - Вип. 32. - С. 131-135.
6. Коршак Є.В. Методика і техніка шкільного фізичного експерименту / Є.В. Коршак, Б.Ю. Миргородський. – К.: Вища школа, 1981. - 280 с.
7. Садовий М.І. Історія фізики з перших етапів становлення до початку ХХІ століття: [навч. пос. для студ. ф.-м. фак. вищ. пед. навч. закл.] / М.І. Садовий, О.М. Трифонова. - Кіровоград: ПП «Центр оперативної поліграфії «Авангард», 2013. - [2-ге вид. переробл. та доп.] - 436 с.
8. Слюсаренко В.В. Методичне забезпечення виконання лабораторних робіт з механіки із новітнім обладнанням «PHYWE»: [пос. для вчит. фізики, учнів шкіл, наук.-пед. прац. та студ. фіз.-мат. фак. вищих пед. навч. закл.] / В.В. Слюсаренко, М.І. Садовий; за ред. М.І. Садового - Кіровоград: Сабоніт, 2013.– 78 с.
9. Слюсаренко В.В. Вивчення коливань зв’язаних маятників за допомогою новітнього обладнання «PHYWE» / В.В. Слюсаренко, М.І. Садовий // Наукові записки. Серія: Педагогічні науки. - 2017. - Вип. 12; Ч. ІІ. - С. 103-109.
10. Шут М.І. Фізика. 9 кл.: [підр. для загальноосв. навч. закл.] / М.І. Шут, М.Т. Мартинюк, Л.Ю. Благодаренко. - К.: «Перун», 2009. - 224 с.


про публікацію авторської розробки
Додати розробку