Фізика. 10 клас. Тема уроку: НАЙПРОСТІШІ КОЛИВАЛЬНІ СИСТЕМИ - МАТЕМАТИЧНИЙ ТА ПРУЖИННИЙ МАЯТНИКИ. ЕНЕРГІЯ КОЛИВАНЬ.

Фізика. 10 клас.

Тема уроку: НАЙПРОСТІШІ КОЛИВАЛЬНІ СИСТЕМИ - МАТЕМАТИЧНИЙ ТА ПРУЖИННИЙ МАЯТНИКИ. ЕНЕРГІЯ КОЛИВАНЬ.

Мета уроку:

• навчальна: сформувати поняття математичного та пружинного маятників як найпростіших моделей коливальних систем; поглибити знання учнів про теорію коливального руху, вивчити формули періодів коливань математичного та пружинного маятників та їх залежність від певних фізичних величин; розглянути закон збереження енергії під час коливального руху маятників; сформувати вміння працювати з графіками гармонічних коливань маятників та записувати рівняння таких коливань за відомими величинами, навчити учнів «читати» графіки гармонічних коливань, зокрема, вміти визначати амплітуду, період, частоту коливань; сформувати вміння аналізувати формулу залежності періоду коливання маятників від довжини нитки та прискорення вільного падіння, коефіцієнта жорсткості та маси маятника і прогнозувати, як змінюється один із параметрів при зміні інших, самостійно проводити вимірювання періодів коливань математичного та пружинного маятників, формувати вміння розв’язувати задачі;
• розвивальна: розвивати спостережливість, уявне і логічне мислення, інтелектуальні та творчі здібності, інтерес до експерименту, вміння аналізувати та робити висновки.
• виховна: виховувати в учнів уміння спілкуватися, працювати у групах, у парах.

Очікувані результати: учні знають і розуміють сутність коливального процесу, умови виникнення вільних коливань, поняття амплітуди, періоду та частоти коливального руху; знають формули періодів математичного та пружинного маятників та застосовують їх для розв'язування задач.

Тип уроку: урок вивчення та засвоєння нових знань.

Методи та прийоми навчання: евристична бесіда, робота у групах, взаємонавчання, «Акваріум», « Інтерв’ю», «Мікрофон»,«Розумова розминка».

Матеріально-технічне забезпечення уроку: ПК, мультимедійний проектор,  екран, дві моделі маятників.

Навчально-методичне забезпечення уроку: підручник Ф. Божинова «Фізика.10 клас», картки для індивідуальної роботи груп, відеоролик «Коливання маятників», картки для «Розумової розминки».

ХІД УРОКУ.

І. Організаційний момент. Налаштування класу на позитивну співпрацю, взаємоповагу один до одного.

ІІ. Актуалізація опорних знань. Пригадаємо який розділ ми вивчаємо. Пригадаємо види коливань у природі. Для цього проведемо «Розумову розминку». Для цього маємо два види карток. Запрошую двох учнів. На кожній з карток зображено види коливань. Один з учнів має відібрати з колоди карт приклади вільних коливання, а інший -  вимушених коливань і записати на дошці їх у два стовпчики: коливання струн музичних інструментів, коливання гойдалки без підштовхування, коливання листя дерев на вітрі, коливання голосових зв'язок у людини, що видають звук, коливання камертона, коливання маятника настінного годинника, рух шальок терезів, коливання голки швейної машинки, коливання тіла на пружині, коливання серця, коливання ножа електробритви, піднімання та опускання руки, коливання моста під ногами людей, рух поршня у циліндрі двигуна, коливання барабанних перетинок у вусі людини, коливання об’єму повітря у легенях, коливання тиску крові у судинах. Далі актуалізуємо знання школярів про те, що всі коливання поділяються на дві групи за часом існування  (затухаючі, незатухаючі) та способом виникнення (вільні, вимушені, автоколивання). Із записаних на дошці коливань прошу здійснити їх розподіл на затухаючі та незатухаючі. Робимо висновки.

ІІІ. Мотивація навчальної діяльності.  Отже, одним з досить  розповсюджених видів нерівномірного руху є коливальний рух. Він часто зустрічається як в природі, так і в техніці. Чим схожі всі ці рухи? (наближено повторюються через певний період часу, характеризуються одними і тими ж величинами).

Для спрощеного вивчення коливальних рухів використовують найпростіші ідеальні моделі коливальної системи – математичний та пружинний маятники. Вони дозволяють дослідити основні властивості і закономірності коливальних рухів, які потім можна застосувати до більш складних коливальних систем.

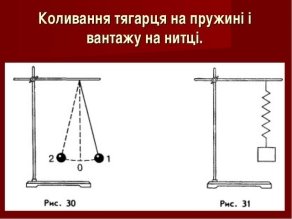ІV. Вивчення нового матеріалу. Записуємо тему уроку. Озвучуємо завдання та мету уроку. Демонструємо презентацію до уроку, де відображено тему, мету, завдання уроку. Демонструю два види маятників. Маятник – це фізичний пристрій, який здійснює коливальні рухи. Питання до класу: Як  по-іншому можна назвати маятники? (коливальні системи). Розглянемо види маятників. Види маятників: математичний та пружинний (демонструю їх моделі). Наголошую учням про складання ними опорного конспекту з даної теми впродовж уроку.

Математичний маятник – це ідеальна коливальна система без тертя, що складається із невагомої й нерозтяжної нитки, на якій підвішена матеріальна точка.

Пружинний маятник — це тіло масою m, закріплене на пружині, жорсткість якої k і яке коливається під дією сили пружності.

         Ці обидва маятники є коливальними системами, у яких можуть відбуватися коливання. Кожна коливальна система має стан рівноваги. Для математичного маятника — це положення, у якому центр мас підвішеної кульки лежить на одній вертикалі з точкою підвісу; у горизонтального пружинного маятника — це положення, у якому пружина не деформована.

Запитання до класу:

-        Як розпочати коливання маятника? (вивести із положення рівноваги);

-        Куди рухатиметься кулька, якщо її відпустити? (до положення рівноваги)

Демонстрація відеоролика «Коливання маятників» про причини руху маятника та взаємні перетворення енергії.

-        Чому маятник рухається до положення рівноваги? (На нього діє рівнодійна сил тяжіння і натягу нитки, направлена до положення рівноваги);

-        Чи зупиняється маятник у положенні рівноваги? (Ні).

        Учні приходять до висновку, що під час коливань маятника відбуваються взаємні перетворення потенціальної і кінетичної енергій.

        Коливальний рух маятників характеризується періодом коливань. Записуємо формули для розрахунку періодів коливань маятників. З‘ясовуємо, які фізичні величини входять у формули: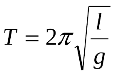

 Ми з вами спробуємо самостійно з’ясувати, від чого залежить період коливань математичного та пружинного маятників. Для цього ділимося на дві команди «Дослідників» та «Ерудитів». Групи отримують завдання на картках для індивідуальної роботи груп. Одна група досліджує коливання математичного маятника, інша - пружинного маятника. Учні висловлюють припущення: від довжини нитки маятника, від амплітуди коливань, від маси кульки, від жорсткості пружини. Учні працюють у групах і перевіряють свої припущення експериментальним способом. Ще одна третя група «Теоретиків» підтверджують теоретично припущення однокласників. Заслуховуємо звіти груп про підтвердження своїх припущень. Робимо висновки. Дивимось презентацію учителя до уроку.

         При невеликих амплітудах маятники здійснюють гармонічні коливання (за малих кутів відхилення 3-5^о). У гармонічних коливаннях сили, під дією яких вони відбуваються, завжди пропорційні до зміщення і спрямовані протилежно до нього (до положення рівноваги). Для пружинного маятника — це сила пружності, для математичного — рівнодійна сили всесвітнього тяжіння та сили натягу нитки. Отже, коливання маятників можна описувати за законами sin або cos. Пропонується самостійна робота учнів з підручником. Записуємо графіки гармонічних коливань для обох маятників та визначаємо за графіком амплітуду коливань, період і частоту за відомими формулами. За відомими графіками визначаємо тип коливань: затухаючі чи незатухаючі.

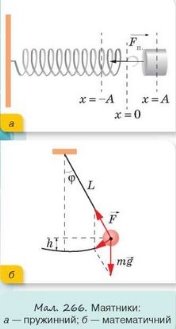          Під час коливань маятників відбуваються взаємні періодичні перетворення потенціальної та кінетичної енергій.

На фізичних моделях учитель з елементами евристичної бесіди демонструє взаємні перетворення енергії при коливальному русі маятників. Група «Теоретиків», які мали випереджувальне завдання, коментують:

    Розглядаючи рухи маятників, вважатимемо, що тертя в обох коливальних системах відсутнє або настільки мале, що ним можна знехтувати. Така система є ізольованою і для неї виконується закон збереження механічної енергії.

У початковий момент (тіло відведено у крайнє ліве положення) коливальна система має максимальну потенціальну енергію.

Для пружинного маятника це:    

для математичного:  

Рухаючись до положення рівноваги, система зменшує потенціальну енергію, але при цьому збільшується її кінетична енергія, яка набуває максимального значення в положенні рівноваги, де швидкість коливного тіла є максимальною.

Для обох маятників: Проходячи положення рівноваги, тіло зменшує кінетичну енергію й, зупиняючись у крайньому правому положенні, має максимальну потенціальну енергію. Кінетична енергія при цьому дорівнює нулю. Таким чином, кінетична енергія коливальної системи матиме максимальні значення в моменти проходження тілом положень рівноваги, а потенціальна — у моменти перебування тіла в точках найбільших відхилень від положення рівноваги. У довільний момент часу сума потенціальної і кінетичної енергії є сталою величиною й дорівнює повній енергії коливань.

Практичне використання маятників. Заслуховуємо учня, який мав випереджувальне завдання. Оскільки будь-який маятник має фіксований період коливань, їх використовують для регулювання ходу годинників. Маятники використовують і в геологічних розвідках. Він коливається з різним періодом у різних точках Землі. Це використовують для відшукання покладів корисних копалин (важких металів, нафти).У місцях, де залягають породи металевих руд, значення g аномально велике. Точні вимірювання прискорення вільного падіння за допомогою математичного маятника дають змогу виявити такі родовища. За допомогою математичного маятника можна виявити добове обертання Землі. Цей дослід у 1851 р. в Парижі виконав Ж. Фуко з маятником завдовжки 67 м. Тому маятники, за допомогою яких можна продемонструвати добове обертання Землі навколо своєї осі, називають маятниками Фуко. Зміст досліду полягає в тому, що площина коливань математичного маятника залишається незмінною відносно інерціальної системи відліку. Тоді відносно неінерціальної системи відліку, пов’язаної із Землею, площина коливань маятника має повертатись. Пізніше цей дослід повторювали в різних місцях. Очевидно, що ефект повороту площини коливань маятника залежить від широти місця проведення досліду, він найбільш виражений на земних полюсах і відсутній на екваторі.

ІV. Закріплення вивченого матеріалу.

Я поміркую й зможу пояснити. Інтерактивна вправа «Акваріум». Учні об’єднуються у внутрішнє коло у три  групи. Кожна група отримує завдання:

Завдання для І групи: Скільки разів протягом періоду гармонічного коливання кінетична енергія системи дорівнює її потенціальній енергії в той самий момент часу? Сталева кулька, підвішена до пружини, здійснює вертикальні коливання. Як зміниться період коливань, якщо до пружини підвісити мідну кульку того самого радіуса? Відповідь обґрунтуйте.

Завдання для ІІ групи: Як зміниться хід годинника з маятником на металевому стержні: а) з підвищенням температури; б) при піднятті на гору; в) при переміщенні від полюса до екватора? Відповідь обґрунтуйте.

Завдання для ІІІ групи: Чи зміниться період коливань гойдалки, якщо хлопчик спершу на ній сидів, а потім встав? Коли замість одної людини на неї сядуть двоє людей? Відповідь обґрунтуйте.

На роботу групи дається 3-5 хв.  Кожна група озвучує ситуацію; обговорює її, використовуючи отримані знання, дискутують; доходять спільного рішення, роблять висновки. Після обговорен­ня, група займає місця у зовнішньому колі, а вчитель ставить класу запитання:

1.Чи погоджуєтесь ви з думкою групи?

2. Чи була ця думка достатньо аргументована, доведена?

3. Який з аргументів ви вважаєте найбільш переконливим?

Розв’язування задач.

Тягар масою 2 кг здійснює горизонтальні коливання на пружині. Амплітуда коливань 5 см, період коливань 5 с. Обчисліть максимальні значення кінетичної та потенціальної енергії, а також швидкість руху тягарця в момент проходження положення рівноваги.

За законом збереження енергії максимальні значення кінетичної й потенціальної енергій рівні між собою. Е « 4 • 10³ Дж. У момент проходження положення рівноваги швидкість руху тягарця максимальна. Її визначаємо з формули:

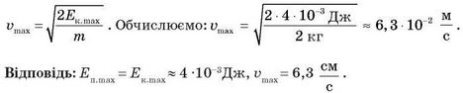
Учнів об’єднуємо у трійки, кожна трійка отримує картку, на якій є задачі й зразок розв’язання. Далі – взаємонавчання.

Задачі для груп:

На картці для груп пропоную зразок розв’язку задачі:

Напишіть рівняння гармонічного коливання тіла, якщо амплітуда коливання 0,2 м, а частота 2 Гц.

Розв’язок:   

Дано:

φ₀₌ 0 ;                         x = A sin (ωt + φ₀);        

А = 0,2 м;                 ν= ω/2π;      

ν = 2 Гц;                  ω=2πν =4π;

Знайти: х(t)-?          Отже:  х(t)=0,2sin4πt. 

Відповідь:   Рівняння гармонічного коливання тіла буде мати такий вигляд: x = 0,2sin4πt. 

1. Математичний маятник зробив 50 коливань за 1 хв 40 с. Визначте його період, частоту та циклічну частоту коливань.

2. Вантаж, маса якого 400 г, коливається горизонтально на пружині, що має жорсткість 250 Н/м. Амплітуда коливань 15 см. Визначте частоту, повну механічну енергію коливань і найбільшу швидкість руху вантажу. Запишіть рівняння коливань.

ІV.  Рефлексія. Підсумок уроку. “Інтерв’ю”. Один із учнів грає роль журналіста, який дізнається в учнів, що було цікавого на уроці, що дізналися, що сподобалося, а що ні. 1. З яких частин складається дана коливальна система? (Показує на один з видів маятників). Який вид коливань у ній виникає?
2. Від чого залежить період коливань цієї системи?
3.Коли коливання можна вважати гармонічними?
4. Як визначити потенціальну енергію тіла, що коливається?  Коли тіло, яке коливається  має максимальне значення кінетичної енергії ?

Інтерактивна вправа «Мікрофон». Продовжіть речення:

1.Ми систематизували на уроці свої знання про……….

2. Що цікавого та нового ми дізналися на уроці?

Домашнє завдання: опрацювати опорний конспект в зошиті та розв’язати задачу:

 І група: 

Коливання вантажу масою 1 кг на пружині описується рівнянням x = 0,1sin(5πt + π _/2). Визначте: а) амплітуду коливання; б) частоту; в) циклічну частоту; г) період; д) початкову фазу коливання.

ІІ група:

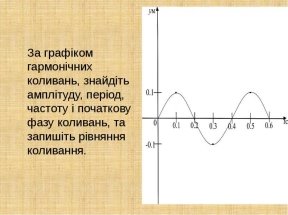
     Для прикладу даємо учням зразок складання опорного конспекту з частини вивчення даної теми, а далі вони в ході уроку самі продовжують його складати. Наголошуємо учням, що зразок опорного конспекту може бути і в іншій довільній формі.

Наприклад: