Розглянемо числову послідовність, перший член якої дорівнює 2, 
а кожний наступний, починаючи з другого, дорівнює попередньому, помноженому на 3:  ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3

Приклади:

•           послідовність степенів 2 є

геометричною

прогресією: 2, 4, 8, 16, 32, ….

•           геометрична

прогресія із першим елементом 3, та знаменником −2:

3, −6, 12, −24, 48,

                   ….                                       

2;  6;  18;  54;  162;  486; … .


ГЕОМЕТРИЧНА ПРОГРЕСІЯ

   Таку послідовність називають геометричною прогресією.

Тобто, послідовність, відмінних від нуля чисел, кожен член якої, починаючи з другого, дорівнює попередньому, помноженому на одне й те саме число - це геометрична прогресія.

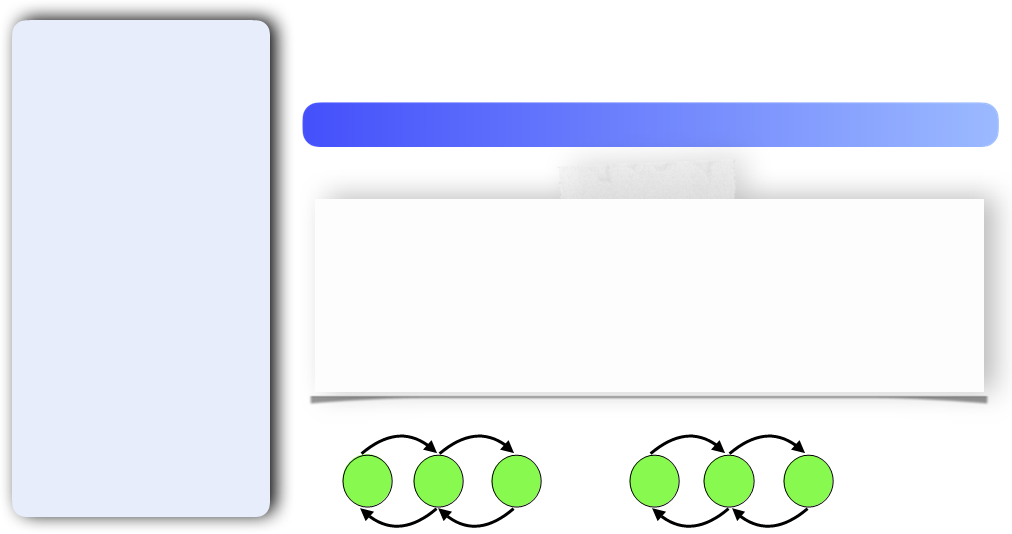 ⋅ q       ⋅ q   ⋅ q   ⋅ q b1 b2         b3 … bn−1 bn bn+1 … : q    : q    : q    : q

  b 1;b₂;b₃;...;b_n−1;b_n;b_n+1;... - члени геометричної прогресії, 
q - це знаменник геометричної прогресії.

  Тому, якщо (b n) - це геометрична прогресія, то виконуються рівності:                                b ₂ = b₁ ⋅ q;b₃ = b₂ ⋅ q;b₄ = b₃ ⋅ q;....

Отже для будь-якого натурального n маємо:

 bn+1 =bn ⋅ q