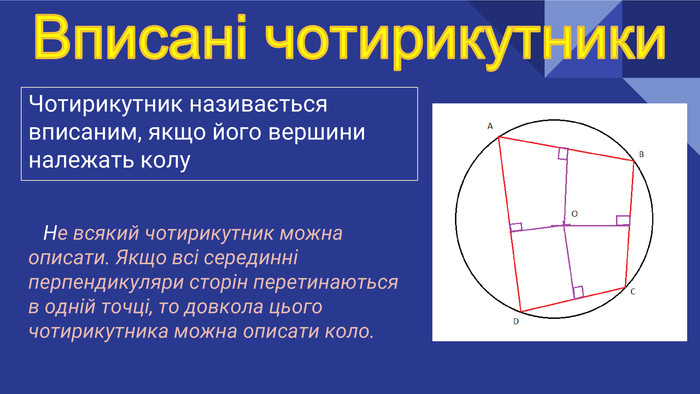
Google Презентація: "Вписані та описані чотирикутники"
Про матеріал
Архів містить файл у форматі .PPTX та Файл для доступу до перегляду та редагування Google-презентації.
Розраховано до підручника: О.С. Істер "Геометрія 8". Нова програма.
Зміст архіву
- та описані чотирикутники.pptx pptx
- .docx docx
Перегляд файлу
Зміст слайдів
Перегляд файлу
Посилання для перегляду (доступно і для редагування):
https://docs.google.com/presentation/d/15jd425fPbicEvEDkjtHvtoQUyauMot3a60XjcB3VE_w/edit?usp=sharing
Середня оцінка розробки
Оцінки та відгуки
zip
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку
























-

Горлова Тетяна
16.11.2023 в 12:16
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Гура Олена Федорівна
20.10.2022 в 07:33
Дякую. Чудово.
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Погорелова Лариса
23.02.2022 в 00:17
Дякую за презентацію - те, що треба для уроку1
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Ирина Ирина
25.11.2021 в 11:36
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Олексюк Катерина Павлівна
18.11.2021 в 07:42
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Чорненька Олена Володимирівна
22.03.2021 в 14:51
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Гайдут Катерина Іванівна
20.11.2020 в 18:03
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Шинкарюк Ольга
09.11.2020 в 21:38
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Шинкарюк Ольга
09.11.2020 в 21:38
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 6 відгуків