Контрольна робота по темі "Теорема Фалеса. Подібні трикутники"

Контрольна робота № 3

Тема: Теорема Фалеса. Подібність трикутників.

Варіант 1

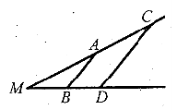
1.       На рисунку 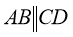, МА=12 см, АС=4 см, BD=6 см. Знайдіть МВ.
2.       Трикутники ABC і 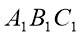подібні, причому сторонам АВ і ВС відповідають сторони 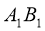і 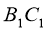. Знайдіть невідомі сторони цих трикутників, якщо АВ = 8 см, ВС = 10 см, 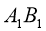=4 см, 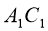=6 см.
3.       Відрізок АК – бісектриса трикутника АВС, АВ=12 см, ВК=8 см, СК=18 см. Знайдіть АС.
4.       У трапеції ABCD з основами AD і BC діагоналі перетинаються в точці О, ВС: AD = 3:5, BD = 24 см. Знайдіть ВО і ОD.
5.       Сторони трикутника дорівнюють 4 см, 7 см і 8 см. Знайдіть сторони подібного йому трикутника, периметр якого дорівнює 57 см.
6.       Периметри подібних трикутників відносяться як 7:5, а сума їх менших сторін дорівнює 36 см. Знайдіть сторони обох трикутників, якщо сторони одного з них відносяться як 3:7:8.

Контрольна робота № 3

Тема: Теорема Фалеса. Подібність трикутників.

Варіант 2

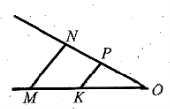
1.       На рисунку 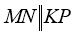, NP=20 см,

PO=8 см, MK=15 см. Знайдіть KO.

2.       Трикутники ABC і 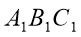подібні, причому сторонам АВ і ВС відповідають сторони 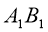і 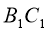. Знайдіть невідомі сторони цих трикутників, якщо BC=5 см, AB=6 см, 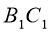=15 см, 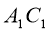=21 см.
3.       Відрізок CD – бісектриса трикутника АВС, АC=12 см, ВC=18 см, AD=10 см. Знайдіть BD.
4.       У трапеції ABCD з основами AD і BC діагоналі перетинаються в точці О, ВO: OD =2:3, AC=25 см. Знайдіть AО і ОC.
5.       Сторони трикутника дорівнюють 3 см, 6 см і 8 см. Знайдіть сторони подібного йому трикутника, периметр якого дорівнює 57 см.
6.       Периметри подібних трикутників відносяться як 3:4, а сума їх середніх  за величиною сторін дорівнює 112 см. Знайдіть сторони обох трикутників, якщо сторони одного з них відносяться як 4:8:7.