Урок з геометрії 8 клас "Теорема Піфагора"

Скарбничка математичних ідей

Без ентузіазму – ніякої математики!

Коли відкриваєш нове, не забувай старого

Навчився сам – навчи двох товаришів.

Мало хотіти, треба діяти!

Чому?!

Математика – гімнастика розуму!

Геометрія 8 клас

Тема:  Теорема Піфагора.

Підготувала

вчитель математики Шеремет В.П.

Пропонований матеріал містить історичні матеріали, різні види вправ та задач, які можна використати при вивченні, повторенні та систематизації знань учнів з теми «Теорема Піфагора».

«Теорема Піфагора – це головна і найкраща теорема геометрії».О.Д.Александров.

Історичні відомості. Піфагор.

Про життя давньогрецького вченого відомо, що він народився на острові Самос, десь у 570 року до н.е. Багато подорожував. Жив у Кротоні (давньогрецька колонія Італії). Там він займався наукою разом зі своїми учнями-піфагорійцями. Все, що відкривали учні, вони приписували своєму вчителеві. Тому з ім’ям Піфагора пов’язано дуже багато наукових відкриттів. У геометрії – це всім відома теорема Піфагора, а також способи побудови деяких правильних многокутників. У географії та астрономії – уявлення про те, що Земля – куля і що існують інші, схожі на неї світи. У музиці – залежність між довжиною струни скрипки та звуком, який вона видає. Подумати тільки, що всі ці відкриття було зроблено дві з половиною тисячі років тому. Не дивно, що після смерті Піфагора було складено про нього багато легенд. Говорили, наприклад, що він ще молодою людиною їздив до Єгипту, дуже довго там жив і вчився у єгипетських жерців. Потім він вирушив подорожувати до Індії та берегів Гангу, де розмовляв зі служителями релігії. Розповідали також, що коли він довів свою відому теорему, то на подяку богам і музам приніс у жертву 100 биків. Можливо цього і не було. А ось відкриття Піфагора та його учнів були, вони живуть і житимуть вічно!

1.Теоретичні відомості: «Хай живе теорія!»

Будь-яка теорія важлива для практики.                        Ч. Колтон.

1. У прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів.
2. Сума кутів трикутника дорівнює 180⁰.
3. Трикутник, у якого є прямий кут, називається прямокутним.
4. Сторони прямокутного трикутника – гіпотенуза та катети.
5. Прямий кут дорівнює 90⁰.
6. Кут, більший за 90⁰ називається тупим.
7. Кут, менший за 90⁰ називається гострим.
8. Прямокутний трикутник зі сторонами 3,  4   і 5, називається єгипетським.
9. У прямокутному трикутнику будь-який з катетів менший за гіпотенузу.
10.       Катет прямокутного трикутника є середнім пропорційним між гіпотенузою і проекцією цього катета на гіпотенузу.
11.       Висота прямокутного трикутника, проведена з вершини прямого кута, є середнім пропорційним між проекціями катетів на гіпотенузу.
12.       Якщо до прямої з однієї точки проведені перпендикуляр і похилі, то:                      а) будь-яка похила більша за перпендикуляр;                                                  б)рівні похилі мають рівні проекції;                                                                                       в)з двох похилих більша та, у якої проекція більша.
13.       У прямокутному трикутнику навпроти кута 30⁰ лежить сторона, що дорівнює половині гіпотенузи.

2.Незакінчені речення:

1. Трикутник, у якого є прямий кут, називається……
2. Сторона прямокутного трикутника, що лежить проти прямого кута, називається…..
3. Прямокутний трикутник зі сторонами 3,  4  і 5  одиниць називається…..
4. Сторони прямокутного трикутника, які утворюють прямий кут, називаються…
5. Квадрат гіпотенузи дорівнює……….
6. Сума кутів у трикутнику дорівнює…….
7. Кут, що дорівнює 90⁰, називається….
8. Кут, більший за прямий, називається…..
9. Кут, менший за прямий, називається….
10.    Сума двох гострих кутів, прямокутного трикутника дорівнює…
11.    Кут, що дорівнює 180⁰, називається….

Розв’язування задач є найбільш характерним і своєрідним різновидом вільного мислення.

У. Джеймс

ЗАВДАННЯ ДЛЯ ЧЕМПІОНІВ:

3.Розв’язати задачі:

1. В прямокутному трикутнику катети дорівнюють 12 см і 5 см. Знайти гіпотенузу.
2. Знайти периметр прямокутника, одна сторона якого дорівнює                                                      12 см, а діагональ 15 см.
3. Діагоналі ромба 24 см та 70 см. Обчислити периметр ромба.
4. У рівнобічній трапеції основи дорівнюють 18 см і 42 см. Бічна сторона 20 см. Обчислити висоту трапеції і середню лінію.
5. Катети прямокутного трикутника відносяться як 1:5. Гіпотенуза дорівнює                               2 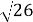м. Знайти катети.
6. Висота рівнобедреного трикутника дорівнює 20 см, а його основа –                                                        30 см. Знайти бічну сторону трикутника.
7. Знайдіть гіпотенузу прямокутного трикутника, якщо його катети дорівнюють        9 м і 12 м.
8. Знайдіть катет прямокутного трикутника, якщо інші його сторони дорівнюють 13 м і 12 м.
9. Катет прямокутного трикутника дорівнює 10 см, а його проекція на гіпотенузу                               8 см. Знайдіть довжину гіпотенузи.
10.    Знайдіть висоту рівнобічної трапеції, основи якої дорівнюють                                                                7 см і 17 см, а бічна сторона 13 см.
11.         Знайдіть катети прямокутного трикутника, якщо його гіпотенуза дорівнює 12 см, а гострий кут 30⁰.
12.         Знайдіть периметр прямокутного трикутника з катетами 5 см і                                                           12 см.

4.Контрольна робота.  Варіант 1.

1. Одна сторона прямокутника дорівнює 7 см, а діагональ – 25 см. Знайдіть другу сторону.
2. Основи рівнобічної трапеції дорівнюють 25 м і 7 м, а висота – 12 м. Знайдіть бічну сторону та діагональ трапеції.
3. Один з катетів прямокутного трикутника на 8 см менший від гіпотенузи, а другий катет дорівнює 16 см. Знайдіть периметр трикутника.

5.Контрольна робота. Варіант 2.

1. У трикутнику АВС, кут С дорівнює 90⁰, АВ=26 см, ВС=10 см. Знайдіть синус кута В, тангенс кута А.
2. Бічна сторона рівнобедреного трикутника дорівнює        26 см, а висота, проведена до його основи, - 10 см. Знайдіть основу трикутника.
3. Основи рівнобічної трапеції дорівнюють 14 см і 32 см   а її висота – 12 см. Знайдіть бічну сторону трапеції.
4. З точки до прямої проведено дві похилі, довжини яких дорівнюють 25 см і 17 см. Знайдіть довжини проекцій цих похилих, якщо вони відносяться як 5:2.

6. Теорема Піфагора. «Мозкова атака».

1. Периметр прямокутника 28 см. Одна сторона його 6 см. Знайти діагональ.
2. Висота рівнобедреного трикутника дорівнює 20 см, а його      основа – 30 см. Знайти бічну сторону трикутника.
3. У рівнобічній трапеції основи дорівнюють 18 см і 42 см. Бічна сторона 20 см. Обчислити висоту трапеції і середню лінію трапеції.
4. Площа квадрата дорівнює 12 см². Чому дорівнює його сторона?
5. Одна зі сторін прямокутника на 3 см більша, ніж інша, а його площа дорівнює 154 см². Знайти сторони прямокутника.
6. Знайти площу ромба, якщо його діагоналі  дорівнюють 10 см і  12 см.
7. Сторони паралелограма дорівнюють 12 см і 15 см. Висота, проведена до більшої сторони, дорівнює 8 см. Знайти другу висоту цього паралелограма.
8. Чому дорівнюють сторони прямокутника, якщо вони відносяться як 3:5, а його площа дорівнює 90 см².
9. Різниця сторін прямокутника дорівнює 7 см, а його діагональ –  13 см. Знайти площу прямокутника.

7.«Запитання для чемпіонів»:

1. Сформулювати теорему Піфагора.
2. Як називаються сторони прямокутного трикутника?
3. Чому дорівнює косинус гострого кута прямокутного трикутника?
4. Чому дорівнює синус гострого кута прямокутного трикутника?
5. Чому дорівнює тангенс гострого кута прямокутного трикутника?
6. Який прямокутний трикутник називається єгипетським?
7. Що таке перпендикуляр і похила?

8.Виберіть неправильне твердження:

1. У прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів.
2. Гіпотенуза прямокутного трикутника більша за кожен із його катетів.
3. Із двох похилих більша та, у якої проекція більша.
4. Катет,  що лежить проти кута 60⁰, дорівнює  половині гіпотенузи.
5. Трикутник, сторони якого дорівнюють 3, 5 і 6, називають єгипетським.

9.Тестові завдання:

1.Знаючи, що діагональ прямокутника дорівнює 13 см,                                                               а одна зі сторін – 12 см, то інша сторона має довжину:                                                  а)5 см;                                                                                                                               б)25 см;                                                                                                                                     в)3 см;                                                                                                                                            г)10 см;                                                                                                                                               д)1 см.

2. Якщо сторона квадрата дорівнює 5 см, то його діагональ дорівнює:                                  а)5 см;                                                                                                                                         б)10 см;                                                                                                                                       в)25 см;                                                                                                                                    г)5 см;                                                                                                                                д)2 см.

3. Якщо сторони паралелограма дорівнюють 5 см і 9 см, то одна з діагоналей паралелограма може дорівнювати:                                                                                     а)1см;                                                                                                                                           б)2 см;                                                                                                                             в)3 см;                                                                                                                                г)4см;                                                                                                                                          д)5 см.

4. Якщо діагональ прямокутника дорівнює 10 см, а кут між діагоналями 60⁰, то більша зі сторін прямокутника дорівнює:                                                              а)5 см;                                                                                                                                    б)6 см;                                                                                                                     в)3 см;                                                                                                                           г)5 см;                                                                                                                                д)2 см.

Це важливо!

10.Співвідношення у прямокутному трикутнику:

1. Синус гострого кута  прямокутного трикутника дорівнює відношенню протилежного катета до гіпотенузи.
2. Косинус гострого кута прямокутного трикутника дорівнює відношенню прилеглого катета до гіпотенузи.
3. Тангенс гострого кута прямокутного трикутника дорівнює відношенню протилежного катета до прилеглого.
4. Котангенс гострого кута прямокутного трикутника дорівнює відношенню прилеглого катета до протилежного.

Хто нічого не знає, тому ні в чому помилятися.

10.                   Тестові завдання.

1. Трикутник, у якого є прямий кут, називається:                                а)гострокутний;   б)тупокутний;   в)прямокутний;   г)рівнобедрений.
2. Найбільша сторона прямокутного трикутника,називається:   а)медіана;   б)катет;  в)гіпотенуза;  г)висота.
3. Сума всіх кутів трикутника дорівнює:                                                                                    а)360⁰;  б)180⁰;   в)90⁰;  г)270⁰.
4. У прямокутному трикутнику прямих кутів може бути:                                               а)один;  б)два;  в)три; г)жодного.
5. Сторони єгипетського трикутника, дорівнюють:                                     а)3, 5 і 6;   б)3,4 і 5;   в)1,2 і 3;   г)1,3 і 5.
6. З однієї точки до прямої можна провести перпендикулярів:                           а) один;  б)два;  в)безліч;   г)жодного.

ІСТОРИЧНА ДОВІДКА:

Теорема Піфагора – основа евклідової геометрії. Завдяки їй можна довести більшість теорем та розв’язати більшість задач геометрії. Цього міцного юнака з товстою шиєю та коротким носом, справжнього забіяку, судді однієї з перших олімпіад не хотіли допускати до змагань, тому що Піфагор був малий на зріст. Але він пробився і «побився» із своїми супротивниками та ще й переміг. Зовсім юним покинув Піфагор свою батьківщину. Він пройшов по дорогах Єгипту і 12 років жив у Вавілоні. Після повернення додому він переселився до Італії, а потім до Сицилії, і ось тут в Кротоні в нього народжується школа під опікою самого тирана Полікрата. Всі учні Піфагора і він сам були працелюбні. Їхніми заповідями були:                                                                                                 1. Роби тільки те, що не засмутить тебе і не примусить розкаюватись. Навчись тому, що слід знати.                                                                                                                                                                                              2.Не нехтуй здоров’ям свого тіла.                                                                                            3.Привчайся жити просто і без розкошів.                                                                                            4.Не закривай очей тоді, коли хочеш спати, не розібравши всіх своїх вчинків за минулий день. Важко сказати, що належало Піфагору, а що його учням. І чи він  вивів паличкою на піску славнозвісну теорему, яка відома кожному учневі, і доведення того, що сума внутрішніх кутів трикутника дорівнює двом прямим кутам? Легенди розповідають, що коли Піфагор довів свою теорему, він віддячив богам, принісши їм у жертву 100 биків. Таким чином, при всіх витратах, у знаменитого філософа із Кротона, першого філософа, достатньо великих фантазій і здогадок. Ось чому люди пам’ятають його дві з половиною тисячі років. Ось чому серед знаменитих олімпійських чемпіонів він довго залишиться найвідомішим, тому що йому випало щастя перемогти не тільки супротивників, але й перемогти час.

*******************************

Вивчення математики передусім сприяє розвиткові логічного мислення, вмінню думати, аналізувати, абстрагувати, схематизувати, узагальнювати. Математика сприяє виробленню раціональних якостей думки та її виражень – творчості, ясності, стислості  тощо, розвиткові спостережливості й уваги, вмінню зосереджуватись, бути наполегливим і послідовним. Ю.О.Митропольський.

************************************

Література:

1. Погорелов А.В. Геометрия 7-9 кл. – К.:Школяр, 2003.
2. Роева Т.Г.,Синельник Л.Я.,Кононенко С.А.                                                                           Геометрия в таблицях 7-9 кл., - Х.: Гимназия, 2001.
3. Журнал «Математика в школах України».