Інтегрований урок "Рух тіла під кутом до горизонту. Формули в табличному процесорі"

Тема: Рух тіла, кинутого горизонтально та під кутом до горизонту.

Мета:

• навчальна: познайомити учнів з рухом тіла, кинутого під кутом до горизонту та особливостями цього руху; набуття вмінь та навичок розв’язувати задачі на рух тіла, кинутого горизонтально та під кутом до горизонту, як окремих випадків руху тіла під дією сили тяжіння; повторення алгоритму побудови графіків руху та швидкості, поняття електронної таблиці, формули, функції, правила запису функцій, надання імен коміркам, копіювання формул за допомогою маркера заповнення та побудову графіків функцій; застосування табличного процесору МS Ехсеl для дослідження руху тіла, кинутого горизонтально та під кутом до горизонту.
• розвиваюча: розвивати просторову уяву під час побудови рисунків та графіків до задач; розширити та поглибити теоретичну базу знань для надання результатам навчання практичної значущості; навички роботи з табличним процесором МS Ехсеl як допоміжним засобом своєї практичної діяльності.
• виховна: виховувати потребу до самоосвіти, уміння оцінювати свою діяльність, здатність до дослідження; формувати компетенції саморозвитку й самоосвіти, комунікативні компетенції.

Тип уроку: Комбінований.

Форма проведення: інтегрований урок з фізики та інформатики.

 

Особливості уроку: використання різних форм роботи на уроці, вивчення історії  розвитку особливостей руху тіла, кинутого під кутом до горизонту; використання нових демонстраційних дослідів з даної теми. 

 

І. Організаційний момент.

 

Вчитель: Сьогодні на уроці ми розглянемо новий вид руху. Зазвичай я формулюю вам тему і мету уроку. Але на цьому уроці ви сформулюєте тему і мету.

 

ІІ. Актуалізація знань.

Повторимо види рухів, які ми вивчали:

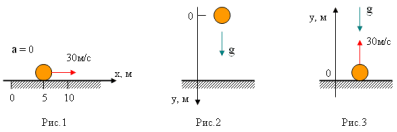
1. рівномірний прямолінійний рух: Записати формули залежності проекції швидкості від часу, переміщення від часу, координати від часу.

 

2. рівноприскорений прямолінійний. Записати формули залежності проекції швидкості від часу, переміщення від часу, координати від часу.

Рух тіла під дією сили тяжіння.

 

3. вільне падіння.

4.  рух тіла, кинутого вертикально вниз.

5. рух тіла, кинутого вертикально вгору.

Питання:

- Під дією якої сили відбувається рух тіла, кинутого вертикально вниз,  вертикально вгору, горизонтально?

- Що називається силою тяжіння?

- Що називається прискоренням вільного падіння?

 

Клас ділиться на групи. Три групи заповнюють перші три рядки таблиці.

Виконати завдання:

Написати рівняння залежності проекції швидкості від часу і координати від часу для тіла, що рухається. Визначити швидкість і координату через 2 с після початку спостереження. Заповнити таблицю.

 

№ малюнку	Рівняння швидкості	Рівняння координат	Час, с	Швидкість, м/с	Координата, м
1			2
2			2
3			2
4			2

 

ІІІ. Постановка проблеми.

• Чому ви не змогли заповнити останній рядок?
• Зустрічається на практиці такий вид руху?
• Яка траєкторія руху тіла, кинутого під кутом до горизонту?

 

Вчитель демонструє дослід Переконуємося в тому, що траєкторія руху тіла, кинутого під кутом до горизонту, є парабола.

 

• Як ви сформулюєте тему і мету нашого уроку?

 

ІV. Вивчення нового матеріалу.

Вчитель: Рух тіла, кинутого під кутом до горизонту з деякою початковою швидкістю являє собою складний рух. Так рухається лижник під час стрибка з трампліну, струмінь води з брандспойта, тенісний м’яч під час удару тенісною ракеткою тощо.

 Вивчення особливостей такого руху почалося в XVI столітті і було пов’язане з появою і удосконаленням артилерійських гармат.

 Уявлення про траєкторію руху артилерійських снарядів на той час були кумедні. Рахувалось, що траєкторія ця складається з трьох частин: А – насильницький рух; В – змішаний рух; С – природний рух, при якому ядро падає на солдат ворога зверху.

 

 Закони польоту снарядів не привертали особливої уваги вчених доти, доки не були винайдені дальнобійні гармати, які посилали снаряд через горби, дерева – так, що людина, яка стріляла не бачила їх польоту.  Стрільба на дальні відстані з таких гармат на початку використовувалась в основному для демонстрації і залякування ворога, а точність стріляння спочатку не мала ніякого значення.

 Близько до правильного рішення питання про політ гарматних ядер дійшов італійський математик Нікколо Тарталья, він розглядає питання траєкторії руху снарядів і стверджує, що ця траєкторія є кривою лінією на протязі всього руху, він показує, що найбільшу дальність польоту снарядів можна досягти під час стрільби під кутом 45⁰ до горизонту та формулює правила стріляння, якими артилеристи керувалися до середини XVIІ століття.

Проте повне рішення проблеми, пов’язане з рухом тіл, кинутих під кутом до горизонту, здійснив італійський астроном і фізик Галілео Галілей.

Заслугою Галілео Галілея стало те, що він вперше запропонував розглядати рух тіла, кинутого під кутом до горизонту як результат складання двох прямолінійних рухів: рівномірного руху по горизонталі і рівноприскореного – по вертикалі.

З’явилася нова наука – балістика. Балістика – розділ механіки, який вивчає рух тіла під впливом сили тяжіння Землі.

Рух тіла, кинутого під кутом до горизонту, характеризується:

• часом польоту (t_пол.);
• дальністю польоту (l);
• найбільшою висотою підняття тіла над горизонтом (h_max).

Постановка проблеми: Від чого будуть залежати ці величини?

Учні: початкової швидкості і кута α до горизонту.

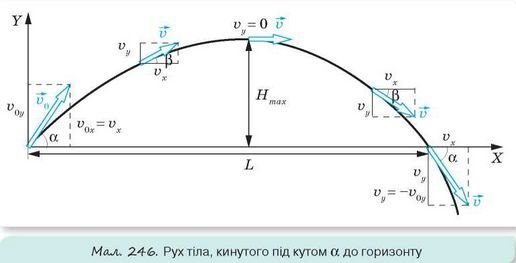
Нехай тіло кинули зі швидкістю під кутом до горизонту. З’єднаємо початок координат з початковим положенням тіла, спрямуємо вісь ОУ вертикально вгору, а вісь ОХ – горизонтально. У обраній системі координат

 

 

Рахуємо, що рух відбувається біля поверхні Землі, тому прискорення тіла – прискорення вільного падіння (а = g) Ми нехтуємо опором повітря, g_x = 0.

 

По осі ОХ рівномірний рух:

 

 

 

По осі ОУ рівноприскорений рух:

 

Доведемо, що траєкторія руху тіла, кинутого під кутом до горизонту є парабола, рахуючи, що по осі ОХ тіло рухається рівномірно, по осі ОУ – рівноприскорено.

 

Відповідь:

   y=

 

 

- рівняння руху.

 

Ми отримали квадратичну залежність між координатами. Тому траєкторія руху тіла, кинутого під кутом до горизонту – парабола. Перевіримо отриману формулу на практиці.

Учитель. Ми маємо на меті з вами застосувати табличний процесор MC Excel для дослідження цих рухів. Тож нам варто пригадати основні поняття і методи роботи в табличному процесорі. Отже,

 

Однією з найпоширеніших електронних таблиць є... (MS Excel), яка входить до пакету програм …(MS Office).

Що називають електронною коміркою?

(Це основний елемент електронної таблиці для зберігання даних)

Що має кожна комірка?

(Адресу)

Які бувають адреси, чим вони відрізняються?

(Абсолютні, відносні та мішані. Абсолютні комірки позначають додаванням знака $ до адреси рядка та стовпця)

Що називають формулою електронної таблиці?

(Це інструкція для обчислення)

Правила запису формул:

1) формула починається зі знака рівності (=);

2) у формулі не має бути   пробілів, за винятком тих, що містяться в текстах;

3)до складу формули можуть входити такі елементи: оператори, посилання на комірки, значення, функції та імена.

Що таке функція електронної таблиці?

(Це результат обчислення деяких аргументів, що перелічуються в дужках після імені функції)

Які функції ми використовуємо? (SIN, COS  та інші)

В якій мірі записується кут в табличному процесорі?

(В радіанах. Тому градусну заздалегідь треба перетворювати на радіани)

Учитель. Зараз ви отримайте картки з завданням для дослідження. Обчислення для побудови зручно виконувати в ЕКСЕЛІ. На роботу у вас 10-15 хв.

 

Картка для учнів.

1. Встановіть пусковий механізм під кутом  до нижнього краю дошки. Зробіть пробний постріл. У місці падіння кульки, на рівні з пусковим механізмом, на нижній край дошки прикріпіть смужку з пластиліну, щоб в результаті наступних пострілів падаюча кулька попадала на нього.
2. Зробіть запуск кульки та за допомогою мірної стрічки виміряйте її дальність польоту (відстань від місця запуску до місця падіння кульки). Виконайте серію пострілів (не менше 3), щоразу вимірюючи дальність польоту. Знайдіть середню дальність польоту кульки
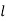
3. Обчисліть початкову швидкість кульки за формулою 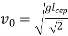та запишіть її значення в лівому кутку міліметрового паперу.
4. На аркуші міліметрового паперу накресліть координатну сітку та прикріпіть до похилої площини так, щоб початок координат збігався точкою запуску кульки. Визначивши в попередньому досліді  початкову швидкість кульки, запишіть рівняння траєкторії .
5. Використовуючи дані рівняння теоретично розрахуйте координати(зручно виконувати в MS Excel) та позначте на аркуші паперу відповідні положення кульки через кожні 0,05 с. Через позначені точки проведіть плавну криву, яка і буде траєкторією руху кульки.
6. Після чого несильно змочіть кульку у воді та запустіть. На папері утвориться мокрий слід, який і буде реальною траєкторією кульки. Наведіть її олівцем. Підпишіть теоретично розраховану та експериментальну траєкторії на вашому рисунку. Продемонструйте отримані криві вчителю.
7. Зробіть висновок, у якому опишіть свої здобутки, яких Ви набули, виконуючи дану роботу; головні причини похибок; основні, на Ваш погляд, недоліки та переваги даного дослідження; пропозиції щодо його покращення.

 

Клас ділиться на 3 групи. Кожна група отримує завдання.

І група Вивести формулу часy польоту.

ІІ група. Вивести формулу  дальності польоту тіла.

ІІІ група. Вивести формулу підйому тіла на максимальну висоту.

Завдання першої групи:

Вивести формулу обчислення часу руху знаючи початкову швидкість

Розв’язання

 Коли тіло перебуває на mах висоті, його швидкість спрямована горизонтально, тобто проекція швидкості на вісь ОУ дорівнює нулю. (υ_у = 0). Оскільки

- час підйому тіла на максимальну висоту.

Оскільки час підйому дорівнює часу падіння, то час польоту вдвічі більший за час підйому:

- час польоту тіла.  

 

Завдання другої групи:

Вивести формулу  дальності польоту тіла, кинутого під кутом до горизонту, знаючи формулу часу польоту тіла і рахуючи, що  по осі ОХ тіло рухається рівномірно.

- час польоту тіла.    2sinα×cosα = sin2α.

 

Відповідь:

  υ₀ ∙ cos α t = υ₀ ∙ cos α=

- дальність польоту тіла.

 

Завдання третьої групи:

Вивести формулу  максимальної висоти підйому тіла, кинутого під кутом до горизонту, знаючи формулу часу польоту тіла і рахуючи, що  по осі ОУ тіло рухається  рівноприскорено.

- час підйому тіла на максимальну висоту.

Відповідь:

h_max = y ==

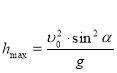  - максимальна висота підйому тіла.

 

Групи звітуються про виконану роботу. Записують формули в зошит.

Вчитель. Визначимо практично за якого кута буде максимальна висота та дальність польоту тіла. Зараз ви отримайте картки з інструкціями дослідження.

 

Картка учнів

1. Встановіть пусковий механізм під кутом до нижнього краю дошки. Зробіть пробний постріл. У місці падіння кульки, на рівні з пусковим механізмом, на нижній край дошки прикріпіть смужку з пластиліну, щоб в результаті наступних пострілів падаюча кулька попадала на нього.
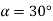
2. Змочіть кульку,  зробіть запуск кульки отримайте на ньому траєкторію руху кульки та обведіть її олівцем, виміряйте її дальність польоту , максимальну висоту підняття кульки вздовж похилої площини та над поверхнею парти (h=s). Підпишіть  траєкторію.
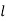
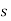
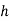
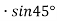
3. Повторіть дослід (пункти 1-2), розташовуючи пусковий механізм під такими кутами:    1) ;              2);              3)
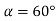
4. Зробіть висновок, у якому опишіть свої здобутки, яких Ви набули, виконуючи дане дослідження; головні причини похибок; основні, на Ваш погляд, недоліки та переваги даного дослідження; пропозиції щодо його покращення.

 

Звітування учнів про виконану роботу висновок з записом в зошит.

 

Учитель. Висоту підняття тіла й дальність польоту можна обчислити за формулами, а можна побудувати графік руху і, використовуючи його, визначити те саме, але з певною точністю. Також можна скористатися табличним процесором. Для початку ми розв’яжемо задачу звичайним способом у зошиті.

Задача №1

Три однакові металеві кульки одночасно кидають з однієї точки і в одному напрямку з початковою швидкістю під такими кутами до горизонту:

    (),         (),         ().

В одній системі координат побудувати графіки руху кульок та, використовуючи їх, порівняти дальності польоту та максимальну висоту підйому кульок. Зробити висновки.

Розв’язання задачі на дошці

Дано     ()     ()     ()	Розв’язок: Максимальна висота підняття тіла та дальність польоту: ,                     ,                      ,                      . Одиниці вимірювання: ,                 Обчислення значень: ,    ,    ,    Відповідь: 1)    ,        , 2)    ,        , 3)    ,        .
-  ?   -  ?

 

 

 

 

Узагальнення результатів у таблиці:

α
	127,6	883,7
	255,1	1020,4
	382,7	883,7

 

У цих задачах ми визначили та .

Питання. Чи підтвердили  залежність дальності польоту й максимальної висоти підняття кульки від кута її кидання?

Висновки учнів

1) Чим більший кут кидання, тим більшою є висота підняття.

2) Найбільша дальність польоту спостерігається за кута 45°.

3) Дальність польоту кульки за 30° та 60° є однаковою.

 

2. Розв’язування задачі № 1 за допомогою табличного процесора МS Ехсеl

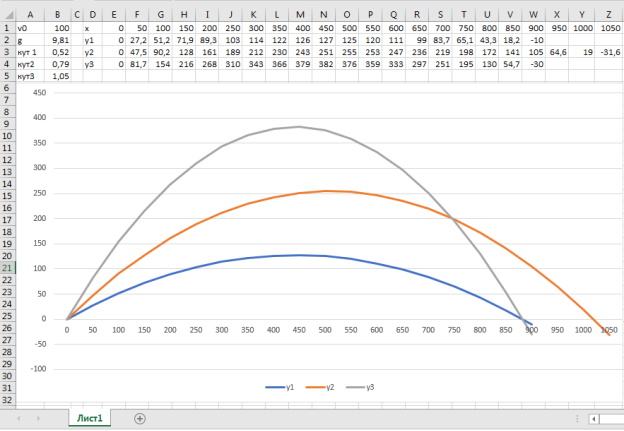
Учитель. Ми розв’язали задачу на дошці, визначивши дальність польоту та максимальну висоту підняття за різних кутів. За умовою задачі нам треба побудувати графіки руху кульок в одній системі координат, тобто виконати функціональну залежність . Ми вже знаємо цю залежність:

.

Побудова графіка руху є досить громіздкою задачею, бо треба визначати чимало точок. Для того, аби спростити розв’язання, ми застосуємо табличний процесор МS Ехсеl. Також ми зможемо наочно побачити траєкторію руху тіла, кинутого під кутом до горизонту на діаграмі. Отже, розпочнемо розв’язання, слідуючи алгоритму:

1. Визначення складу та структури таблиці.

2. Надання імен коміркам, що містять значення певних фізичних величин:

3. Обчислення значень координати у, які відповідають  значенням координати х, для всіх трьох випадків значення кутів за формулою:

,

Закріплення вивченого матеріалу:

 

• Який вид руху ми вивчили?
• Яка траєкторія руху тіла, кинутого під кутом до горизонту?
• Як Галілео Галілей запропонував розглядати цей вид руху?
• Якими величинами характеризується рух тіла, кинутого під кутом до горизонту?
• Де на практиці зустрічаємо такий вид руху?
• Чи спрощує обчислення використання тем вивчених на інших уроках.

 

Домашнє завдання: конспект уроку, заповнити 4 рядок таблиці, розв’язати задачу.

Невелику металеву кульку кидають під кутом     () до горизонту з початковою швидкістю . Визначити час польоту, максимальну висоту підняття, дальність польоту кульки та побудувати графік руху кульки для випадків, коли набуватиме таких значень:

а) , б) , в) , г) .

Порівняти отримані результати та зробити висновки.