Інтегрований урок з фізики в 10 класі ГРАФІКИ ЗАЛЕЖНОСТІ КІНЕМАТИЧНИХ ВЕЛИЧИН ПІД ЧАС РІВНОПРИСКОРЕНОГО ПРЯМОЛІНІЙНОГО РУХУ З ВИКОРИСТАННЯМ ВЛАСТИВОСТЕЙ ЛІНІЙНОЇ ФУНКЦІЇ

Відділ  освіти Корсунь – Шевченківської райдержадміністрації

Корсунь – Шевченківський районний методичний кабінет

Корсунь – Шевченківська загальноосвітня школа

I – III ступенів №1

Корсунь – Шевченківської районної ради

 

 

Антонов Дмитро Володимирович, вчитель фізики вищої кваліфікаційної категорії, вчитель - методист

Жирна Катерина Володимирівна, вчитель математики вищої кваліфікаційної категорії, вчитель - методист

 

 

 

Інтегрований урок з фізики в 10 класі

ГРАФІКИ ЗАЛЕЖНОСТІ КІНЕМАТИЧНИХ ВЕЛИЧИН ПІД ЧАС РІВНОПРИСКОРЕНОГО ПРЯМОЛІНІЙНОГО РУХУ З ВИКОРИСТАННЯМ ВЛАСТИВОСТЕЙ ЛІНІЙНОЇ ФУНКЦІЇ

 

 

 

 

 

 

 

 

 

Корсунь – Шевченківський - 2018 р.

    МЕТА: формування предметних компетентностей учнів під час вивчення фізики та математики, обґрунтувати необхідність вивчення матеріалу, розширити уяву про можливість застосування графіків залежності кінематичних величин під час вивчення математики, реалізувати наскрізні лінії на уроках фізики шляхом забезпечення формування ціннісних і світоглядних орієнтацій учнів, що визначить їх наступну поведінку в життєвих ситуаціях.

                         Тип уроку: інтегрований урок.

Хід уроку

І. Організаційна частина

     Організовую класний колектив до роботи.

ІІ. Актуалізація та мотивація навчальної діяльності учнів

     Згадаємо вигляд закону зміни швидкості рівномірного руху:

υ= υ₀ +at;  s=υ₀t + at²/2.

    Якщо врахувати, що s=x=x₀, то

x=x₀+ υ₀t + at²/2;

s_x= υ_x² – υ_0x²/2a_x.

ІІІ. Вивчення нового  матеріалу

    Почнемо діти наш урок з розгляду графіків лінійної функції в математиці.

  - Яким словом можна замінити слово «функція» ?

                                                           (залежність)

 

- Всесвіт, природа, життя побудовані на залежностях. Наведіть приклади таких залежностей.

                                                            ( відстань під час руху тіла залежить від 

                                                              швидкості  і часу; робітник залежить від

                                                              керівника; дитина від батьків; одяг від 

                                                              погоди або за потребою…)

- Як можна задавати такі залежності ?

                                                      (словесно; таблицею; графічно; формулою;…)

- Які функції вивчили ?

                                                            (лінійну; квадратичну; степеневу;

                                                             показникову; логарифмічну;

                                                             тригонометричні;…; їм обернені; …)

- Яка функція називається лінійною ?

                                                             ( … х – аргумент, незалежна

                                                               змінна,  у – функція, що залежить від х,           

                                                              - числа …)

- Що можна сказати про функції, задані формулами       ?

                                                            ( формули учні бачать на екрані монітора )

- Яка формула задає лінійну функцію ?

                                                             (       

 

                                                               )

                                                              ( формули проектуються)

- Що є графіком лінійної функції ?

                                                              ( пряма)

- Задайте формулою лінійну функцію.  .

- За допомогою цієї формули повторимо властивості лінійних функцій                    

                                                             (запитання на маніторі)

1) знайти значення функції, якщо значення аргументу  -2;

2) при якому значенні аргументу функція дорівнює 3?

3) знайдіть координати точок перетину графіка функції з осями координат;

4) знайдіть область визначення  функції ;

5) знайдіть область значень функції;

6) назвіть нулі функції;

7) назвіть проміжки знакосталості функцій ;

8) парна чи непарна дана функція ?

                                                        (коли буде непарною, парною ?)

9) зростаюча чи спадна функція ?

10) назвіть найбільше значення функції;  найменше;

11) назвіть функцію, графік якої паралельний графіку даної функції;

                                                       ( перпендикулярний);

12) назвіть функцію , графік якої перетинає графік даної функції.

 

Самостійна робота.

       Дано лінійну функцію 

1.Знайдіть значення функці, якщо значення аргументу 7.

        а) – 32      б) 0,2    в) -0,8    г) -2    д) -0,4.

2. Знайти значення аргументу, якщо значення функції дорівнює 3.

        а)  0    б) -12    в) 12    г) -5    д) 7.

3. Знайдіть нулі даної функції.

        а)  0  і  3     б) -3 і 3      в) -3      г) 0      д) 3.

4. Знайдіть    в даній лінійній функції.

        а)  3  і  -1     б) -1 і 3      в) -0,2  і  0,6       г) 0,6  і  -0,2       д) -3,2  і  1,2.

5. Зростаюча чи спадна дана функція ?

        а) ні зростаюча, ні спадна     б) спадна   в) зростаюча   г) стала   д) не можна

        визначити.

6. Розв′яжіть нерівність   у > 0.

         а)    б)    в)   г)      д)

 А тепер, шановні учні, повернемось до фізики.

 Якщо порівняти графіки проекцій швидкості тіла у рівноприскореному русі, де υ = const з випадком, коли a= const, то стає зрозумілим, що графіки ідентичні.

МАЛ.28

 

 

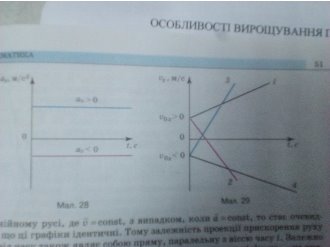
Графік проекції швидкості руху тіла:

υ_x= υ(t).

  З рівняння υ_x = υ_0x +a_xt видно, що залежність є лінійною. Залежно від значення проекції прискорення і початкової швидкості υ_0x і a_x  графіки мають такий вигляд:

МАЛ.29

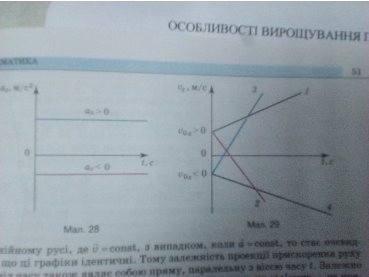
   Якщо υ_0x= 0, то пряма виходить з початку координат і залежно  від значення прискорення буде напрямлена або вгору (a_x > 0)  або вниз (a_x< 0) .

 

Графік руху тіла  тіла x = x(t)

  Кінематичне рівняння  x=x₀+ υ_0xt + a_xt²/2;

  Тому графік залежності координати тіла від часу є парабола, гілки якої згідно з параметрами руху мають різні вигляди.

 

МАЛ.30

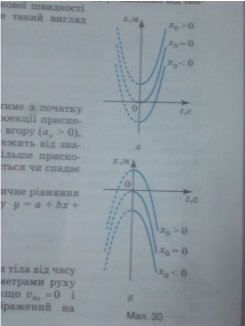
ІV. Закріплення нового матеріалу.

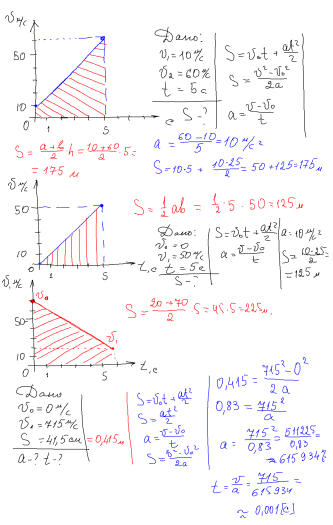
V. Домашнє завдання.

1.Прочитати та розібрати §12

2.Дати відповіді на запитання ст.52.

3.Розвязати задачі № 40;41;42;61;62;64.,ст. 61-62.