Календарне планування з алгебри 7 клас
ÓÄÊ 373.167.1:512
Ì52
Ðåêîìåíäîâàíî
̳í³ñòåðñòâîì îñâ³òè ³ íàóêè Óêðà¿íè
(ëèñò ÌÎÍ Óêðà¿íè â³ä 03.06.2020 ¹ 1/11-3693)
Âèäàíî çà ðàõóíîê äåðæàâíèõ êîøò³â. Ïðîäàæ çàáîðîíåíî
Ìåðçëÿê À. Ã.
Ì52 Àëãåáðà : ï³äðó÷. äëÿ 7 êë. çàêëàä³â çàã. ñåðåä. îñâ³òè / À. Ã. Ìåðçëÿê, Â. Á. Ïîëîíñüêèé, Ì. Ñ. ßê³ð. — 2-ãå âèä., ïåðåðîáë. — Õ. : óìíàç³ÿ, 2020. — 288 ñ. : ³ë.
ISBN 978-966-474-341-6.
ÓÄÊ 373.167.1:512
© À. Ã. Ìåðçëÿê, Â. Á. Ïîëîíñüêèé, Ì. Ñ. ßê³ð, 2015
© À. Ã. Ìåðçëÿê, Â. Á. Ïîëîíñüêèé, Ì. Ñ. ßê³ð, ïåðåðîáëåííÿ, 2020
© ÒΠÒÎ «Ã³ìíàç³ÿ», îðèã³íàë-ìàêåò,
ISBN 978-966-474-341-6 õóäîæíº îôîðìëåííÿ, 2020
![]()
ЛЮБІ СЕМИКЛАСНИКИ ТА СЕМИКЛАСНИЦІ!
Ви починаєте вивчати новий шкільний предмет — алгебру.
Алгебра — це стародавня й мудра наука. На вас чекає знайомство з її азами. Знати алгебру надзвичайно важливо. Мабуть, немає сьогодні такої галузі знань, де не застосовувалися б досягнення цієї науки: у фізиці та хімії, астрономії та біології, географії та економіці, навіть у мовознавстві та історії використовують «алгебраїчний інструмент».
Алгебра — не тільки корисний, а й дуже цікавий предмет, який розвиває кмітливість і логічне мислення. І ми сподіваємося, що ви в цьому скоро переконаєтеся за допомогою підручника, який три- маєте в руках. Ознайомтеся з його будовою.
Текст підручника поділено на чотири параграфи, кожний з яких складається з пунктів. У пунктах викладено теоретичний матеріал. Найважливіші відомості виділено жирним шрифтом і курсивом.
Зазвичай виклад теоретичного матеріалу завершується прикладами розв’язування задач. Ці записи можна розглядати як один із можливих зразків оформлення розв’язання.
До кожного пункту дібрано завдання для самостійного розв’язування, приступати до яких радимо лише після засвоєння теоретичного матеріалу. Серед завдань є як прості й середні за складністю вправи, так і важкі задачі (особливо ті, що позначено зірочкою (*)).
Кожний пункт завершується рубрикою «Учимося робити нестандартні кроки». До неї дібрано задачі, для розв’язування яких потрібні не спеціальні алгебраїчні знання, а лише здоровий глузд, винахідливість і кмітливість. Ці задачі корисні, як вітаміни. Вони допоможуть вам навчитися приймати несподівані й нестандартні рішення не тільки в математиці, а й у житті.
У рубриці «Коли зроблено уроки» ви зможете прочитати оповідання з історії алгебри.
Дерзайте! Бажаємо успіху!
Від авторів
ШАНОВНІ КОЛЕГИ ТА КОЛЕЖАНКИ!
У книзі дібрано великий і різноманітний дидактичний матеріал. Проте за один навчальний рік усі задачі розв’язати неможливо, та в цьому й немає потреби. Разом з тим набагато зручніше працювати, коли є значний запас задач. Це дає можливість реалізувати принципи рівневої диференціації та індивідуального підходу в навчанні.
Ми дуже сподіваємося, що цей підручник стане надійним помічником у вашій нелегкій та шляхетній праці, і будемо щиро раді, якщо він вам сподобається.
Зеленим кольором позначено номери задач, що рекомендовано для домашньої роботи, синім кольором — номери задач, що рекомендовано для розв’язування усно.
У деяких пунктах частину тексту розміщено на кольоровому фоні. Так виокремлено матеріал, який на ваш розсуд можна віднести до необов’язкового для вивчення.
Бажаємо творчої наснаги й терпіння.
![]()
|
n° |
завдання, що відповідають початковому та середньому рівням навчальних досягнень; |
|
n• |
завдання, що відповідають достатньому рівню навчальних досягнень; |
|
n•• |
завдання, що відповідають високому рівню навчальних досягнень; |
|
n* |
задачі для математичних гуртків і факультативів; |
|
p |
закінчення доведення теореми; |
![]()
¤ закінчення розв’язування прикладу;
¿ завдання, які можна виконувати за допомогою комп’ю тера; рубрика «Коли зроблено уроки».
Алгебра — для вас новий шкільний предмет. Проте ви вже знайомі з «азбукою» цієї науки. Так, коли ви записували формули та складали рівняння, вам доводилося позначати числа буквами, «будуючи» буквені вирази.
Наприклад, записи a2, (x + y)2, 2 (a + b), x y z , abc, m є бук-
2 n
веними виразами.
Наголосимо, що не будь-який запис, складений із чисел, букв, знаків арифметичних дій і дужок, є буквеним виразом. Наприклад, запис 2x + ) – ( є беззмістовним набором символів.
Разом з тим вираз, складений з однієї букви, вважають буквеним виразом.
Розглянемо буквений вираз 2 (a + b). Ви знаєте, що за його допомогою можна знайти периметр прямокутника зі сторонами a і b. Якщо, наприклад, букви a і b замінити відповідно числами 3 і 4, то дістанемо числовий вираз 2 (3 + 4). За таких умов периметр прямокутника дорівнюватиме 14 одиницям довжини. Число 14 називають значенням числового виразу 2 (3 + 4).
Зрозуміло, що замість букв a і b можна підставляти й інші числа, отримуючи щоразу новий числовий вираз.
Оскільки букви можна заміняти довільними числами, то ці букви називають змінними, а сам буквений вираз — виразом зі змінними (або зі змінною, якщо вона одна).
Розглянемо вираз 2x + 3. Якщо змінну x замінити, наприклад, числом ![]() , то дістанемо числовий вираз 2æ
, то дістанемо числовий вираз 2æ![]() +3. При цьому говорять, що
+3. При цьому говорять, що ![]() — значення змінної x, а число 4 — значення виразу
— значення змінної x, а число 4 — значення виразу
2x + 3 при x = ![]() .
.
Числові вирази та вирази зі змінними називають алгебраїчними виразами.
Розглянемо дві групи алгебраїчних виразів:
|
І група |
ІІ група |
|
x – y3 |
1 x |
|
a 4 |
a
(a+b)2 |
|
1 b2 +5a 3 |
m n +3 |
|
mn 7 |
x 5 − 2 y |
Вирази кожної групи містять такі дії: додавання, віднімання, множення, піднесення до степеня, ділення. Однак вирази першої групи не містять ділення на вирази зі змінними. Тому вирази першої групи називають цілими виразами. Вирази другої групи не є цілими.
У 7 класі ми вивчатимемо цілі вирази.
![]() ПРИКЛАД Значення змінних a, b і m такі, що a – b = 4, m = –5. Чому дорівнює значення виразу 7bm – 7am?
ПРИКЛАД Значення змінних a, b і m такі, що a – b = 4, m = –5. Чому дорівнює значення виразу 7bm – 7am?
Розв’язання. Використовуючи розподільну та сполучну властивості множення, отримуємо:

|
1.° Знайдіть значення числового виразу: |
|
|
1) 0,72 + 3,018; 3) 1,8æ0,3; |
5) 72 : 0,09; |
|
2) 4 – 2,8; 4) 5,4 : 6; 2.° Чому дорівнює значення виразу: |
6) 9 : 4. |
1) ![]() +
+ ![]() ; 3)
; 3) ![]() æ
æ![]() ; 5)
; 5) ![]() :
: ![]() ;
;
2) ![]() −
− ![]() ; 4)
; 4) ![]() æ18; 6)
æ18; 6) ![]() : 4;
: 4;
1. Вступ до алгебри
7) 10 : ![]() ; 9) 6 −1
; 9) 6 −1![]() ; 11) 8
; 11) 8 ![]() æ1
æ1![]() ; 8) 2
; 8) 2![]() +4
+4 ![]() ; 10) 4
; 10) 4 ![]() −1
−1![]() ; 12) 1
; 12) 1![]() :5
:5![]() ?
?
|
3.° Обчисліть значення виразу: |
|
|
1) 3,8 + (–2,5); 6) 0 – 7,8; |
11) −48æ0; |
|
2) –4,8 + 4,8; 7) 0 – (–2,4); |
12) –3,3 : (–11); |
|
3) –1 + 0,39; 8) –4,5 – 2,5; |
13) 3,2 : (–4); |
3
4) 9,4 – (–7,8); 9) 8æ(−0,4); 14) ![]() ;
;
2
5) 4,2 – 5,7; 10) −1,2æ(−0,5); 15) 1![]() .
.
4.° Чому дорівнює значення виразу:
1) 18![]() −
−![]() æ1
æ1![]() −
−![]() æ
æ![]() ; 4)
; 4) ![]() :
: ![]() ;
;
2) 6 ![]() 5
5![]() :1
:1![]() æ
æ![]() ; 5) 3
; 5) 3![]() 2
2![]() : 5
: 5![]() ?
?
3) ( 1,42 ( 3,22)) : ( 0,4) ( 6)æ( 0,7);
5.° Обчисліть значення числового виразу:
1) 14![]() −3
−3![]() æ
æ![]() −1
−1![]() æ
æ![]() ;
;
2) 5![]() :1
:1![]() 1
1![]() æ
æ![]() ;
;
3) ( 3,25 2,75) : ( 0,6) 0,8æ( 7);
4) 1![]() 2
2![]() : 5
: 5![]() .
.
6.° Складіть числовий вираз і знайдіть його значення:
1) добуток суми чисел –12 і 8 та числа 0,5;
2) сума добутку чисел –12 і 8 та числа 0,5;
3) частка суми й різниці чисел –1,6 і –1,2; 4) квадрат суми чисел –10 і 6;
5) сума квадратів чисел –10 і 6.
7.° Складіть числовий вираз і знайдіть його значення:
1) частка від ділення суми чисел ![]() і −
і −![]() на число −
на число −![]() ;
;
2) різниця добутку чисел –1,5 і 4 та числа 2; 3) добуток суми та різниці чисел –1,9 і 0,9; 4) куб різниці чисел 6 і 8.
8.° Знайдіть значення виразу:
1) 2x – 3 при x = 4; 0; –3;
2) ![]() a +
a + ![]() b при a = –6, b = 16;
b при a = –6, b = 16;
3) 3m – 5n + 3k при m = –7, n = 1,4, k = –0,1.
9.° Обчисліть значення виразу: 1) 0,4y + 1 при y = –0,5; 8; –10; 2) ![]() c −0,2d при c = –28, d = 15.
c −0,2d при c = –28, d = 15.
|
10.° Які з даних виразів є цілими: |
|
|
1) 7a + 0,3; 3) a+b; c |
3m 5 5) + ; 5 3m |
![]() 2) 5x y; 4) a+b; 6) 9x 5y 1?
2) 5x y; 4) a+b; 6) 9x 5y 1?
4 z
11.° Користуючись термінами «сума», «різниця», «добуток», «частка», прочитайте алгебраїчні вирази та вкажіть, які з них є цілими:
|
1) a – (b + c); |
4) 2m – 10; |
7) ac + bc; |
|
2) a + bc; |
a c 5) + ; b d |
a 8) ; b+ 4 |
|
3) x − y; |
6) (a + b) c; |
9) (a – b) (c + d). |
z
12.° Запишіть у вигляді виразу:
1) число, протилежне числу a;
2) число, обернене до числа a;
3) суму чисел x і y;
4) число, обернене до суми чисел x і y;
5) суму чисел, обернених до чисел x і y;
6) суму числа a та його квадрата;
7) частку від ділення числа a на число, протилежне числу b; 8) добуток суми чисел a і b та числа, оберненого до числа c; 9) різницю добутку чисел m і n та частки чисел p і q.
13.° Олівець коштує x грн, а зошит — y грн. Запишіть у вигляді
виразу зі змінними:
1) скільки коштують 5 олівців і 7 зошитів;
2) на скільки більше треба заплатити за a зошитів, ніж за b олівців.
14.° Робітнику видали заробітну плату однією купюрою номіналом 100 грн, a купюрами номіналом 50 грн і b купюрами по 20 грн. Запишіть у вигляді виразу зі змінними, яку суму грошей отримав робітник.
1. Вступ до алгебри
15.• Із двох міст, відстань між якими дорівнює 300 км, вирушили одночасно назустріч один одному два автомобілі зі швидкостями m км/год і n км/год. Запишіть у вигляді виразу зі змінними, через скільки годин після початку руху вони зустрі- нуться.
16.• Із двох селищ, відстань між якими дорівнює s км, одночасно в одному напрямі вирушили пішохід і велосипедист. Пішохід іде попереду зі швидкістю a км/год, а велосипедист їде зі швидкістю b км/год. Запишіть у вигляді виразу зі змінними, через скільки годин після початку руху велосипедист наздожене пішохода. Обчисліть значення отриманого виразу при a = 4, b = 12, s = 12.
17.• Запишіть у вигляді виразу:
1) потроєний добуток різниці чисел a і b та їхньої суми;
2) суму трьох послідовних натуральних чисел, менше з яких дорівнює n;
3) добуток трьох послідовних парних натуральних чисел, більше з яких дорівнює 2k;
4) число, у якому a тисяч, b сотень і c одиниць;
5) кількість сантиметрів у x метрах і y сантиметрах; 6) кількість секунд у m годинах, n хвилинах і p секундах.
18.• Запишіть у вигляді виразу:
1) добуток чотирьох послідовних натуральних чисел, більше з яких дорівнює x;
2) різницю добутку двох послідовних непарних чисел і меншого з них, якщо більше число дорівнює 2k + 1;
3) кількість кілограмів у a тоннах і b центнерах.
19.•• Складіть вирази для обчислення довжини синьої лінії та площі фігури, яку вона обмежує (рис. 1).
c d c d c d c
|
|
c |
|
||||
|
b |
|
|
||||
|
|
d |
|||||
|
|
||||||
b b 
a a a а б в
Рис. 1
20.•• Складіть вирази для обчислення довжини синьої лінії та площі фігури, яку вона обмежує (рис. 2).
c c c c a
|
d |
|
d |
|
d |
|
d |
|
|
|
|
b 
a c а б
Рис. 2
21.•• Значення змінних a і b такі, що a + b = –8, c = 4. Чому дорівнює значення виразу:
1) a + b – c; 3) 3ac + 3bc?
2) 0,5 (a + b) + c;
22.•• Значення змінних m і n такі, що m – n = 5, k = –2. Чому дорівнює значення виразу:
1) (n – m) k; 2) 2m – 2n + 3k?
![]()
23. (Задача з українського фольклору.) Мірошник бере за роботу ![]() змеленого борошна. Скільки пудів борошна намололи селя-
змеленого борошна. Скільки пудів борошна намололи селя-
нину, якщо додому він повіз 99 пудів?
24. До їдальні завезли капусту, моркву та картоплю. Капусти було 64 кг, маса моркви становила ![]() маси капусти, а маса картоплі — 180 % маси моркви. Скільки всього кілограмів овочів завезли до їдальні?
маси капусти, а маса картоплі — 180 % маси моркви. Скільки всього кілограмів овочів завезли до їдальні?
25. Відомо, що a і b — натуральні числа, а число a — правильний b
дріб. Чи можна стверджувати, що:
1) a – b > 0; 2) 1 > 1; 3) b > a? a b a b
Книга про відновлення та протиставлення
![]() ГОТУЄМОСЯ ДО ВИВЧЕННЯ НОВОЇ ТЕМИ
ГОТУЄМОСЯ ДО ВИВЧЕННЯ НОВОЇ ТЕМИ
26. Доведіть, що:
1) число 5 є коренем рівняння 3x + 1 = 21 – x; 2) число –2 не є коренем рівняння x (x + 4) = 4.
27. Розв’яжіть рівняння:
1) 0,3x = 9; 2) –2x = 3; 3) 15x = 0.
28. Розкрийте дужки:
1) 2 (x – 3y + 4z); 2) –0,4 (–5 + 1,5y).
29. Зведіть подібні доданки:
1) 4a + 9a – 18a + a; 2) 1,2a – a + b – 2,1b.
30. Розкрийте дужки та зведіть подібні доданки:
1) (x + 3,2) – (x + 4,5); 2) 1,4 (a – 2) – (6 – 2a).
31. Знайдіть корінь рівняння:
1) 2x – 7 = x + 4; 2) –0,7 (5 – x) = –4,9.
Поновіть у пам’яті зміст пп. 27, 28 на с. 272, 273.
![]() УЧИМОСЯ РОБИТИ НЕСТАНДАРТНІ КРОКИ
УЧИМОСЯ РОБИТИ НЕСТАНДАРТНІ КРОКИ
32. Дано 12 натуральних чисел. Доведіть, що з них завжди можна вибрати два, різниця яких ділиться націло на 11.
![]() Книга про відновлення та протиставлення
Книга про відновлення та протиставлення
Готуючись до нової теми, ви повторили основні властивості рівнянь (пп. 27, 28 на с. 272, 273). Знаменно, що з однією із цих властивостей пов’язано походження слова «алгебра».
У ІХ ст. видатний учений Мухаммед ібн Муса аль-Хорезмі (що означає Мухаммед, син Муси, із Хорезма) написав трактат про способи розв’язування рівнянь. У ті часи від’ємні числа вважали хибними, брехливими, абсурдними. Тому якщо під час розв’язування рівнянь отримували «хибне» число, то його перетворювали на «справжнє», переносячи в іншу частину рівняння. Таке перетворення Мухаммед аль-Хорезмі назвав відновленням (арабською

Мухаммед ібн Муса аль-Хорезмі
(IX ст.)
Середньоазіатський математик, астроном і географ. Він був пер-
шим, хто у своїх наукових працях розглядав
алгебру як самостійний розділ математики.
мовою — «аль-джебр»). Знищення однакових членів в обох частинах рівняння він назвав протиставленням (арабською мовою — «альмукабала»).
Сам трактат мав назву «Коротка книга про відновлення та протиставлення» (арабською мовою — «Кітаб аль-мухтасар фі хісаб аль-джебр ва-аль-мукабала»).
Слово «аль-джебр» із часом перетворилося на добре відоме всім слово «алгебра».
У ХІІ ст. праці аль-Хорезмі було перекладено латинською мовою. У середньовічній Європі ім’я аль-Хорезмі записували як Algorizmi, і багато правил з його праць починалися словами Dixit Algorizmi («Алгоризмі сказав»). Поступово стали звикати, що із цих слів починається багато правил, а слово Algorizmi перестали пов’язувати з ім’ям автора. Так виник термін «алгоритм», яким позначають процес, що дозволяє за скінченну кількість кроків отримати розв’язок задачі.
З такими процесами ви докладно ознайомитеся на уроках інформатики.
§ 1 ЛІНІЙНЕ РІВНЯННЯ
З ОДНІЄЮ ЗМІННОЮ
•  У цьому параграфі ви повторите властивості рівнянь, зможете вдосконалити навички розв’язування рівнянь і задач на складання рівнянь.
У цьому параграфі ви повторите властивості рівнянь, зможете вдосконалити навички розв’язування рівнянь і задач на складання рівнянь.
• Ви дізнаєтеся, що багато відомих вам рівнянь можна об’єднати в один клас.
2. Лінійне рівняння з однією змінною
Розглянемо три рівняння:
2x = –3, 0x = 0, 0x = 2.
Число –1,5 є єдиним коренем першого рівняння.
Оскільки добуток будь-якого числа на нуль дорівнює нулю, то коренем другого рівняння є будь-яке число.
Третє рівняння коренів не має.
Незважаючи на істотні відмінності отриманих відповідей, наведені рівняння зовні схожі: усі вони мають вигляд ax = b, де x — змінна, a і b — деякі числа.
Рівняння виду ax = b, де x — змінна, a і b — деякі числа, називають лінійним рівнянням з однією змінною.
Наведемо ще приклади лінійних рівнянь:
![]() x =7; –0,4x = 2,8; –x = 0.
x =7; –0,4x = 2,8; –x = 0.
Зауважимо, що, наприклад, рівняння x2 = 0, (x – 2) (x – 3) = 0, | x | = 5 не є лінійними.
Текст, виділений жирним шрифтом, роз’яснює зміст терміна «лінійне рівняння з однією змінною». У математиці речення, яке розкриває сутність терміна (поняття, об’єкта), називають означенням.
Отже, ми сформулювали (або, як говорять, дали) означення лінійного рівняння з однією змінною.
Розв’яжемо рівняння ax = b для різних значень a і b.
1) Якщо a ≠ 0, то, поділивши обидві частини рівняння ax = b на a, отримаємо x = b. Тоді можна зробити такий висновок: a
якщо a ≠ 0, то рівняння ax =b має єдиний корінь, що дорів-
нює b.
a
2) Якщо a = 0, то лінійне рівняння набуває такого вигляду: 0x = b.
Тоді можливі два випадки: b = 0 або b ≠ 0.
У першому випадку отримуємо рівняння 0x = 0. Тоді можна зробити такий висновок: якщо a = 0 та b = 0, то рівняння ax = b має безліч коренів: будь-яке число є його коренем.
У другому випадку, коли b ≠ 0, то при будь-якому значенні x маємо хибну рівність 0x = b. Тоді можна зробити такий висновок: якщо a = 0 та b ≠ 0, то рівняння ax = b коренів не має.
Отримані висновки подамо у вигляді таблиці.
|
Значення a і b |
a ≠ 0 |
a = 0, b = 0 |
a = 0, b ≠ 0 |
|
Корені рівняння ax = b |
x = b a |
x — будь-яке число |
Коренів немає |
![]() ПРИКЛАД 1 Розв’яжіть рівняння:
ПРИКЛАД 1 Розв’яжіть рівняння:
1) (3x + 2,1) (8 – 2x) = 0; 2) | 5x – 6 | = 4.
Розв’язання. 1) Ви знаєте, що добуток кількох множників дорівнює нулю тоді, коли принаймні один із множників дорівнює нулю, і навпаки, якщо хоча б один із множників дорівнює нулю, то й добуток дорівнює нулю. Тому для розв’язування даного рівняння достатньо розв’язати кожне з рівнянь:
3x + 2,1 = 0, 8 – 2x = 0.
Звідси x = –0,7 або x = 4. Відповідь: –0,7; 4.
2) Ураховуючи, що існують тільки два числа, –4 і 4, модулі яких дорівнюють 4, отримуємо:
5x – 6 = 4 або 5x – 6 = –4.
![]() Звідси x = 2 або x = 0,4. Відповідь: 2; 0,4.
Звідси x = 2 або x = 0,4. Відповідь: 2; 0,4. ¤
Звертаємо вашу увагу на те, що наведені рівняння не є лінійними, проте розв’язування кожного з них зводиться до розв’язування лінійного рівняння.
![]() ПРИКЛАД 2 Розв’яжіть рівняння:
ПРИКЛАД 2 Розв’яжіть рівняння:
1) (a – 1) x = 2; 2) (a + 9) x = a + 9.
Розв’язання. 1) При a = 1 рівняння набуває вигляду 0x = 2.
У цьому випадку коренів немає. При a ≠ 1 отримуємо: x 2 .
a 1
Відповідь: якщо a = 1, то рівняння не має коренів; якщо a ≠ 1, то x 2 .
a 1
2) При a = –9 рівняння набуває вигляду 0x = 0. У цьому випадку коренем рівняння є будь-яке число. При a ≠ –9 отримуємо: x = 1.
Відповідь: якщо a = –9, то x — будь-яке число;  якщо a ≠ –9, то x = 1.
якщо a ≠ –9, то x = 1. ¤
33.° Які з наведених рівнянь є лінійними:
1) 3x = 6; 3) x2 = 4; 5) 4 =2; 7) x = 0;
x
2) x = 4; 4) | x | = 2; 6) ![]() x = 2; 8) 0x = 8?
x = 2; 8) 0x = 8?
34.° Чи є число 4 коренем рівняння:
1) 4x = 12; 2) ![]() x =1; 3) 0x = 0; 4) 0x = 4?
x =1; 3) 0x = 0; 4) 0x = 4?
|
35.° Скільки коренів має рівняння: |
|
|
1) 3x = –10; 2) 0x = 6; 3) 0x = 0; 36.° Розв’яжіть рівняння: |
4) 5x = 0? |
1) ![]() x =1; 3) –1,4x = –2,1;
x =1; 3) –1,4x = –2,1;
2) 3x ![]() ; 4)
; 4) ![]() x 6.
x 6.
37.° Розв’яжіть рівняння:
1) 6x ![]() ; 3)
; 3) ![]() x =12;
x =12;
2) 0,1x = –2,75; 4) ![]() x
x ![]() .
.
|
38.° Розв’яжіть рівняння: |
|
|
1) 18 – 16x = –30x – 10; |
4) 6x – 19 = –2x – 15; |
|
2) –7x + 2 = 3x – 1; |
5) 0,2x + 3,4 = 0,6x – 2,6; |
3) 10 – 2x = 12 + x; 6) ![]() x 12
x 12 ![]() x 2.
x 2.
|
39.° Знайдіть корінь рівняння: |
|
|
1) 10x + 7 = 8x – 9; |
3) 2,7 + 1,9x = 2x + 1,5; |
2) 20 – 3x = 2x – 45; 4) ![]() x 13
x 13 ![]() x 8.
x 8.
|
40.° Розв’яжіть рівняння: |
|
|
1) –3 (x – 4) = 5x – 12; |
3) 26 – 4x = 3x – 7 (x – 3); |
|
2) (16x – 5) – (3 – 5x) = 6; 41.° Розв’яжіть рівняння: |
4) –2 (3 – 4x) + 5 (2 – 1,6x) = 4. |
|
1) 4 (13 – 3x) – 17 = –5x; |
3) 14 – x = 0,5 (4 – 2x) + 12; |
|
2) (18 – 3x) – (4 + 2x) = 10; 42.• Доведіть, що: |
4) 4x 3 (20 x) 10x 3 (11 x). |
1) коренем рівняння 4 (x – 5) = 4x – 20 є будь-яке число; 2) рівняння 2y – 8 = 4 + 2y не має коренів.
43.• Розв’яжіть рівняння:
1) 0,8 – (1,5x – 2) = –0,8 + 4,5x;
2) 0,6x – 5 (0,3x + 0,2) = 0,5 (x – 1) – 0,8;
3) ![]() y 7
y 7 ![]() y 1
y 1![]() ;
;
4) ![]() (5,4 8,1y) 0,03
(5,4 8,1y) 0,03 ![]() (6,8 3,4y).
(6,8 3,4y).
44.• Знайдіть корінь рівняння:
1) 0,9x – 0,6 (x – 3) = 2 (0,2x – 1,3);
2) –0,4 (3x – 1) + 8 (0,8x – 0,3) = 5 – (3,8x + 4);
3) ![]() (0,56 4,2y) 0,4
(0,56 4,2y) 0,4 ![]() (0,52 6,5y).
(0,52 6,5y).
45.• Розв’яжіть рівняння:
1) 8 (7x – 3) = –48 (3x + 2); 2) 4,5 (8x + 20) = 6 (6x + 15).
46.• Чому дорівнює корінь рівняння:
1) –36 (6x + 1) = 9 (4 – 2x); 2) 3,2 (3x – 2) = –4,8 (6 – 2x)?
47.• Розв’яжіть рівняння:
1) (4x – 1,6) (8 + x) = 0; 3) (3x 2) 4 ![]() x 0;
x 0;
|
2) x (5 – 0,2x) = 0; 48.• Розв’яжіть рівняння: |
4) (2x 1,2) (x 1) (0,7x 0,21) |
0. |
|
1) (1,8 – 0,3y) (2y + 9) = 0; |
2) (5y + 4) (1,1y – 3,3) = 0. |
|
49.• Розв’яжіть рівняння:
1) 5x 4 16x 1; 2) 4y 33 17 y .
2 7 3 2
50.• Знайдіть корінь рівняння:
![]() 1) ; 2) 5x 3 x 5.
1) ; 2) 5x 3 x 5.
5 8
51.• Чому дорівнює корінь рівняння:
1) 2x 5x 23; 2) x x 7 ; 3) 3x 4 x ?
3 4 6 8 36 10 15 6
52.• Розв’яжіть рівняння:
7x 5x 4 ; 2) 2x x 15; 3) x 1 x .
1)
6 18 27 7 4 14 8 12
53.• При якому значенні змінної:
1) значення виразу 4x – 0,2 (8x – 7) дорівнює –22,6;
2) вирази 0,2 (3 – 2y) і 0,3 (7 – 6y) + 2,7 набувають рівних значень;
3) значення виразу 0,6y на 1,5 більше за значення виразу 0,3 (y – 4);
4) значення виразу 5x – 1 у 5 разів менше від значення виразу 6,5 + 2x?
54.• При якому значенні змінної:
1) вирази 6 – (2x – 9) і (18 + 2x) – 3 (x – 3) набувають рівних значень;
2) значення виразу –4 (2y – 0,9) на 2,4 менше від значення виразу 5,6 – 10y?
55.• Розв’яжіть рівняння:
|
1) | x | + 6 = 13; 4) | x – 5 | = 4; |
7) | 3x + 4 | = 2; |
|
2) | x | – 7 = –12; 5) | 9 + x | = 0; |
8) | 2x + 1 | + 13 = 14; |
|
3) 7 | x | – 3 = 0; 6) | x – 4 | = –2; 56.• Розв’яжіть рівняння: |
9) | | x | – 3 | = –5. |
|
1) | x | – 8 = –5; 3) | x + 12 | = 3; |
5) | 10x – 7 | – 32 = –16; |
2) | x | + 5 = 2; 4) | 8 – 0,2x | = 12; 6) | | x | – 2 | = 2.
57.• При якому значенні a рівняння:
1) 5ax = –45 має корінь, що дорівнює числу 3;
2) (a – 4) x = –5a + 4x – 7 має корінь, що дорівнює числу –6?
58.• При якому значенні a рівняння:
1) 3ax = 12 – x має корінь, що дорівнює числу –9; 2) (5a + 2) x = 8 – 2a має корінь, що дорівнює числу 2?
59.• Укажіть яке-небудь значення b, при якому буде цілим числом корінь рівняння:
1) 0,1x = b; 2) bx = 21; 3) ![]() x = b; 4) bx =
x = b; 4) bx = ![]() .
.
60.• Складіть рівняння, яке:
1) має єдиний корінь, що дорівнює числу –4; 2) має безліч коренів; 3) не має коренів.
61.•• Знайдіть усі цілі значення m, при яких є цілим числом корінь рівняння:
1) mx = 3; 2) (m + 4) x = 49.
62.•• Знайдіть усі цілі значення n, при яких є натуральним числом корінь рівняння:
1) nx = –5; 2) (n – 6) x = 25.
63.•• При якому значенні b мають один і той самий корінь рівняння:
1) 7 – 3x = 6x – 56 і x – 3b = –35;
2) 2y – 9b = 7 і 3,6 + 5y = 7 (1,2 – y)?
64.•• При якому значенні c мають один і той самий корінь рівняння:
1) (4x + 1) – (7x + 2) = x і 12x – 9 = c + 5; 2) ![]() cx x c і 6 – 3 (2x – 4) = –8x + 4?
cx x c і 6 – 3 (2x – 4) = –8x + 4?
65.•• При якому значенні a не має коренів рівняння:
1) ax = 6; 2) (3 – a) x = 4; 3) (a – 2) x = a + 2? 66.•• При якому значенні a будь-яке число є коренем рівняння:
1) ax = a; 2) (a – 2) x = 2 – a; 3) a (a + 5) x = a + 5?
67.•• При яких значеннях a має єдиний корінь рівняння:
1) (a – 5) x = 6; 2) (a + 7) x = a + 7?
68.•• Розв’яжіть рівняння:
1) (b + 1) x = 9; 2) (b2 + 1) x = –4.
69.•• Розв’яжіть рівняння (m + 8) x = m + 8.
70.•• Яким виразом можна замінити зірочку в рівності 6x + 8 = 4x + *, щоб утворилося рівняння, яке:
1) не має коренів; 2) має безліч коренів; 3) має один корінь?
71.•• У рівності 2 (1,5x – 0,5) = 7x + * замініть зірочку таким виразом, щоб утворилося рівняння, яке:
1) не має коренів; 2) має безліч коренів; 3) має один корінь.
72.* Розв’яжіть рівняння:
1) | x | + 3x = 12; 2) | x | – 4x = 9; 3) 2 (x – 5) – 6 | x | = –18.
73.* Розв’яжіть рівняння:
1) 2x – | x | = –1; 2) 7 | x | – 3 (x + 2) = –10.
74.* При яких цілих значеннях a корінь рівняння:
1) x – 2 = a; 2) x + 7a = 9; 3) 2x – a = 4; 4) x + 2a = 3 є цілим числом, яке ділиться націло на 2?
75.* При яких цілих значеннях b корінь рівняння:
1) x + 3 = b; 2) x – 2 = b; 3) x – 3b = 8 є цілим числом, яке ділиться націло на 3?
76.* При яких значеннях b корінь рівняння є меншим від b:
1) 3x = b; 2) x = 2b?
77.* При яких значеннях d корінь рівняння є більшим за d:
1) 4x = d; 2) ![]() x = d?
x = d?
![]()
78. Олеся та Микола живуть у селі Грушеве, а навчаються в різ-них університетах міста Києва. До Центрального залізничного вокзалу Києва вони їдуть електропотягом.
В університеті, де вчиться Олеся, заняття починаються о 8:30, а на шлях від залізничного вокзалу до університету вона витрачає 35 хв. В університеті, де вчиться Микола, заняття починаються о 9:00, а на шлях від вокзалу до університету він витрачає 40 хв. У таблиці наведено фрагмент розкладу руху електропотягів.
|
Відправлення від станції Грушеве |
Прибуття на вокзал у Київ |
|
6:27 |
7:23 |
|
6:39 |
8:00 |
|
6:45 |
8:08 |
|
7:15 |
8:23 |
О котрій годині найпізніше може виїхати Олеся, а о котрій — Микола, щоб не запізнитися на заняття?
79. Один робітник може виконати завдання за 45 год, а другому для цього потрібно в 1![]() раза менше часу, ніж першому. За скільки годин вони виконають завдання, працюючи разом? Яку частину завдання при цьому виконає кожен із них?
раза менше часу, ніж першому. За скільки годин вони виконають завдання, працюючи разом? Яку частину завдання при цьому виконає кожен із них?
80. За перший день Олена прочитала ![]() сторінок книжки, за другий —
сторінок книжки, за другий — ![]() сторінок книжки та за третій день — решту 12 сторінок. Скільки сторінок у цій книжці?
сторінок книжки та за третій день — решту 12 сторінок. Скільки сторінок у цій книжці?
81. Відомо, що n — натуральне число. Яким числом, парним чи непарним, є значення виразу:
1) 4n; 2) 2n – 1; 3) n (n + 1)?
82. Чи є правильним твердження, що при будь-якому значенні a:
1) 2a > a; 2) 2 | a | > | a |?
 УЧИМОСЯ РОБИТИ НЕСТАНДАРТНІ КРОКИ
УЧИМОСЯ РОБИТИ НЕСТАНДАРТНІ КРОКИ
83. Скільки існує шестицифрових чисел, у записі яких є хоча б одна парна цифра?
![]() 3. Розв’язування текстових задач
3. Розв’язування текстових задач
Вам неодноразово доводилося розв’язувати задачі за допомогою складання рівнянь. Різноманітність цих задач є найкращим підтвердженням універсальності цього методу. У чому ж секрет його сили?
Річ у тім, що умови несхожих між собою задач удається записати математичною мовою. Отримане рівняння — це результат перекладу умови задачі з української мови математичною.
Часто умова задачі є описом якоїсь реальної ситуації. Складене за цією умовою рівняння називають математичною моделлю даної ситуації.
Зрозуміло, щоб отримати відповідь, рівняння треба розв’язати. Для цього в алгебрі розроблено різні методи та прийоми. З деякими з них ви вже знайомі, вивчення багатьох інших на вас ще чекає.
Знайдений корінь рівняння — це ще не відповідь задачі. Треба з’ясувати, чи не суперечить отриманий результат реальній ситуації, яка описана в умові задачі.
Розглянемо, наприклад, такі задачі.
1) За 4 год зібрали 6 кг ягід, причому кожної години збирали однакову за масою кількість ягід. Скільки кілограмів ягід збирали щогодини?
2) Кілька хлопчиків зібрали 6 кг ягід. Кожен із них зібрав по 4 кг. Скільки хлопчиків збирали ягоди?
За умовою обох задач можна скласти одне й те саме рівняння 4x = 6, коренем якого є число 1,5. Проте в першій задачі відповідь «щогодини збирали 1,5 кг ягід» є прийнятною, а в другій — «ягоди збирали півтора хлопчика» — ні. Тому друга задача не має розв’язків.
Під час розв’язування задач на складання рівнянь бажано дотримуватися такої послідовності дій:
1) за умовою задачі скласти рівняння (побудувати математичну модель задачі);
2) розв’язати отримане рівняння;
3) з’ясувати, чи відповідає знайдений корінь змісту задачі, і дати відповідь.
Цю послідовність дій, яка складається з трьох кроків, можна назвати алгоритмом розв’язування текстових задач.
![]() ПРИКЛАД 1 Робітник мав виконати замовлення за 8 днів. Проте, виготовляючи щодня 12 деталей понад норму, він уже за 6 днів роботи не тільки виконав замовлення, а й виготовив додатково 22 деталі. Скільки деталей щодня виготовляв робітник?
ПРИКЛАД 1 Робітник мав виконати замовлення за 8 днів. Проте, виготовляючи щодня 12 деталей понад норму, він уже за 6 днів роботи не тільки виконав замовлення, а й виготовив додатково 22 деталі. Скільки деталей щодня виготовляв робітник?
Розв’язання. Нехай робітник виготовляв щодня x деталей. Тоді за нормою він мав виготовляти щодня (x – 12) деталей, а всього їх мало бути виготовлено 8 (x – 12). Насправді він виготовив 6x деталей. Оскільки за умовою значення виразу 6x на 22 більше за значення виразу 8 (x – 12), то отримуємо рівняння 6x – 22 = 8 (x – 12).
Тоді 6x – 22 = 8x – 96;
6x – 8x = –96 + 22;
![]() –2x = –74; x = 37. Відповідь: 37 деталей.
–2x = –74; x = 37. Відповідь: 37 деталей. ¤
![]() ПРИКЛАД 2 Велосипедистка проїхала 65 км за 5 год. Частину шляху вона їхала зі швидкістю 10 км/год, а решту — зі швидкістю 15 км/год. Скільки часу вона їхала зі швидкістю 10 км/год і скільки — зі швидкістю 15 км/год?
ПРИКЛАД 2 Велосипедистка проїхала 65 км за 5 год. Частину шляху вона їхала зі швидкістю 10 км/год, а решту — зі швидкістю 15 км/год. Скільки часу вона їхала зі швидкістю 10 км/год і скільки — зі швидкістю 15 км/год?
Розв’язання. Нехай велосипедистка їхала x год зі швидкістю 10 км/год. Тоді зі швидкістю 15 км/год вона їхала (5 – x) год. Перша частина шляху становить 10x км, а друга — 15 (5 – x) км.
Оскільки весь шлях складав 65 км, то маємо рівняння 10x + 15 (5 – x) = 65.
Звідси 10x + 75 – 15x = 65;
–5x = –10; x = 2.
Отже, зі швидкістю 10 км/год вона їхала 2 год, а зі швидкістю 15 км/год — 3 год.
![]() Відповідь: 2 год, 3 год.
Відповідь: 2 год, 3 год. ¤
Ви добре знаєте, що складання рівнянь — це не єдиний спосіб розв’язування текстових задач. Також ефективним прийомом є «розв’язування задач по діях», тобто в арифметичний спосіб, коли в певній послідовності знаходять значення числових виразів
|
і в кінцевому результаті отримують відповідь. Тут перекладом задачі з реального життя математичною мовою є запис одного або кількох числових виразів. Зауважимо, що в початковій школі саме із цього способу ви почали знайомство з методами розв’язування текстових задач. Методи розв’язування задач, які являють собою реальні ситуації, різноманітні й далеко не вичерпуються моделями у вигляді числових виразів або рівнянь. Вивчаючи математику, ви розширюватиме список відповідних моделей. Зараз ознайомимося з методом, застосування якого засновано на побудові математичної моделі у вигляді геометричної фігури. Зазначимо, що ви вже використовували елементи цього прийому, коли в задачах на рух будували різні схеми: руху в одному напрямі, у протилежних напрямах, назустріч один одному й т. п.
Розв’язання. Побудуємо схему, на якій міста будуть зображені точками А, В, C, D і Е. Дорогу, яка сполучає два міста, зображатимемо у вигляді відрізка. Наприклад, на рисунку 3 показано кільцеву схему доріг.
AC E D Рис. 3 Рис. 4 1) Задача зводиться до того, щоб з’ясувати, чи можна п’ять точок площини сполучити відрізками так, щоб із кожної точки виходили чотири відрізки. На рисунку 4 показано, як це зробити. 2) Припустимо, що така схема є можливою. Підрахуємо, скільки відрізків буде на цій схемі. Маємо: 5æ3 = 15 (відрізків). Проте при такому підрахунку кожний відрізок було враховано двічі. Отримуємо, що кількість відрізків дорівнює Отримали суперечність.
|
![]()
84.° Ганна купила 24 зошити, причому зошитів у лінійку вона купила на 6 більше, ніж зошитів у клітинку. Скільки зошитів кожного виду купила Ганна?
85.° Із двох дерев зібрали 65,4 кг вишень, причому з одного дерева зібрали на 12,6 кг менше, ніж із другого. Скільки кілограмів вишень зібрали з кожного дерева?
86.° Периметр прямокутника дорівнює 7,8 см, а одна з його сторін на 1,3 см більша за другу. Знайдіть сторони прямокутника.
87.° Одна зі сторін прямокутника в 11 разів менша від другої. Знайдіть сторони прямокутника, якщо його периметр дорівнює 144 см.
 88.° Три найвищі гірські вершини України — Говерла, Бребенескул і Петрос знаходяться в найвищому гірському масиві Чорногори в Карпатах. Сума їхніх висот дорівнює 6113 м, причому Говерла на 29 м вища за Бребенескул і на 41 м вища за Петрос. Знайдіть висоту кожної з вершин.
88.° Три найвищі гірські вершини України — Говерла, Бребенескул і Петрос знаходяться в найвищому гірському масиві Чорногори в Карпатах. Сума їхніх висот дорівнює 6113 м, причому Говерла на 29 м вища за Бребенескул і на 41 м вища за Петрос. Знайдіть висоту кожної з вершин.
89.° Три найглибші печери України — Гора Говерла Солдатська, Каскадна та Нахімовська знаходяться в Криму. Сума їхніх глибин дорівнює 1874 м, причому глибина Каскадної в 1,2 раза менша від глибини Солдатської та на 26 м більша за глибину Нахімовської. Знайдіть глибину кожної з печер.
90.° У будинку є 160 квартир трьох видів: однокімнатні, двокімнатні та трикімнатні. Однокімнатних квартир у 2 рази менше, ніж двокімнатних, і на 24 менше, ніж трикімнатних. Скільки в будинку квартир кожного виду?
91.° Троє робітників виготовили 96 деталей. Один із них виготовив у 3 рази більше деталей, ніж другий, а третій — на 16 деталей більше, ніж другий. Скільки деталей виготовив кожний робітник?
92.• У трьох цехах заводу працює 101 робітниця. Кількість робітниць першого цеху становить ![]() кількості робітниць третього цеху, а кількість робітниць другого цеху — 80 % кількості робітниць третього. Скільки робітниць працює в першому цеху?
кількості робітниць третього цеху, а кількість робітниць другого цеху — 80 % кількості робітниць третього. Скільки робітниць працює в першому цеху?
93.• Велосипедисти взяли участь у триденному поході. За другий і третій дні вони проїхали відповідно 120 % і ![]() відстані, яку подолали за перший день. Який шлях вони проїхали за перший день, якщо довжина всього маршруту становить 270 км?
відстані, яку подолали за перший день. Який шлях вони проїхали за перший день, якщо довжина всього маршруту становить 270 км?
94.• У 6 великих і 8 маленьких ящиків розклали 232 кг яблук. Скільки кілограмів яблук було в кожному ящику, якщо в кожному маленькому ящику було на 6 кг яблук менше, ніж у кожному великому?
95.• У двох залах кінотеатру 534 місця. В одному залі 12 однакових рядів, а в другому — 15 однакових рядів. У кожному ряду першого залу на 4 місця більше, ніж у кожному ряду другого. Скільки місць у кожному залі кінотеатру?
96.• Відстань між двома містами мотоциклістка проїхала за 0,8 год, а велосипедист — за 4 год. Швидкість велосипедиста на 48 км/год менша від швидкості мотоциклістки. Знайдіть швидкості мотоциклістки та велосипедиста.
97.• За 2 кг цукерок одного виду заплатили стільки, скільки за 3,5 кг цукерок другого виду. Яка ціна кожного виду цукерок, якщо 1 кг цукерок першого виду на 12 грн дорожчий за 1 кг цукерок другого виду?
98.• Кілограм огірків на 0,8 грн дешевший від кілограма помідорів. Скільки коштує 1 кг помідорів, якщо за 3,2 кг помідорів заплатили стільки ж, скільки за 3,6 кг огірків?
99.• В одному баку було в 3 рази більше води, ніж у другому. Коли в перший бак долили 16 л води, а в другий — 80 л, то в обох баках води стало порівну. Скільки літрів води було спочатку в кожному баку?
100.• На одній полиці було в 4 рази більше книжок, ніж на другій. Коли з першої полиці взяли 5 книжок, а на другу поставили 16 книжок, то на обох полицях книжок стало порівну. Скільки книжок було спочатку на кожній полиці?
101.• Зараз батькові 26 років, а його синові — 2 роки. Через скільки років батько буде в 5 разів старший за сина?
102.• Зараз матері 40 років, а її доньці — 18 років. Скільки років тому донька була в 3 рази молодша від матері?
103.• Для шкільної бібліотеки придбали 40 орфографічних і тлумачних словників української мови, заплативши разом 690 грн. Скільки було словників кожного виду, якщо орфографічний словник коштує 15 грн, а тлумачний — 24 грн?
104.• Вкладник поклав у банк 3000 грн на два різних депозитних рахунки, причому за першим рахунком йому нараховували 7 % річних, а за другим — 8 % річних. Через рік він одержав 222 грн прибутку. Яку суму було внесено на кожний рахунок? 105.• У касі було 19 купюр по 2 і 5 гривень на загальну суму 62 грн. Скільки купюр кожного виду було в касі?
106.• У двох сховищах була однакова кількість вугілля. Коли з першого сховища вивезли 680 т вугілля, а з другого — 200 т, то в першому залишилося в 5 разів менше вугілля, ніж у другому. Скільки тонн вугілля було в кожному сховищі спочатку?
107.• У Марини й Василя було порівну грошей. Коли на купівлю книжок Марина витратила 30 грн, а Василь — 45 грн, то в Марини залишилось у 2 рази більше грошей, ніж у Василя. Скільки грошей було в кожного з них спочатку?
108.• В одному мішку було в 5 разів більше борошна, ніж у другому. Коли з першого мішка пересипали 12 кг борошна в другий мішок, то маса борошна в другому мішку склала ![]() маси борошна в першому. Скільки кілограмів борошна було в кожному мішку спочатку?
маси борошна в першому. Скільки кілограмів борошна було в кожному мішку спочатку?
109.• В одному контейнері було в 3 рази більше вугілля, ніж у другому. Коли з першого контейнера пересипали 300 кг вугілля в другий контейнер, то маса вугілля в першому контейнері склала 60 % маси вугілля в другому. Скільки кілограмів вугілля було в кожному контейнері спочатку?
110.• Одному робітникові треба було виготовити 90 деталей, а другому — 60. Перший робітник щодня виготовляв 4 деталі, а другий — 5 деталей. Через скільки днів першому робітникові залишиться виготовити вдвічі більше деталей, ніж другому, якщо вони почали працювати одночасно?
111.• В одній цистерні було 200 л води, а в другій — 640 л. Коли з другої цистерни використали вдвічі більше води, ніж із першої, то в другій залишилося в 3,5 раза більше води, ніж у першій. Скільки літрів води використали з кожної цистерни?
112.• Із двох міст, відстань між якими дорівнює 385 км, виїхали назустріч один одному легковий і вантажний автомобілі. Легковий автомобіль їхав зі швидкістю 80 км/год, а вантажний — 50 км/год. Скільки часу їхав до зустрічі кожен із них, якщо вантажний автомобіль виїхав на 4 год пізніше за легковий?
113.• З одного села до другого вирушив пішохід зі швидкістю 4 км/год, а через 1,5 год після цього з другого села назустріч йому виїхав велосипедист зі швидкістю 16 км/год. Через скільки хвилин після виїзду велосипедист зустрівся з пішоходом, якщо відстань між селами дорівнює 14 км?
114.• Відстань між двома містами річкою на 55 км менша, ніж по шосе. З одного міста до другого можна дістатися теплоходом за 6 год, а по шосе автобусом — за 3 год 30 хв. Знайдіть швидкості автобуса й теплохода, якщо швидкість теплохода на 30 км/год менша від швидкості автобуса.
115.• Теплохід пройшов 4 год за течією річки та 3 год проти течії. Шлях, який пройшов теплохід за течією, на 48 км більший за шлях, пройдений ним проти течії. Знайдіть швидкість теплохода в стоячій воді, якщо швидкість течії дорівнює 2,5 км/год.
116.• Турист і туристка плили 5 год на плоту за течією річки та 1,5 год на моторному човні проти течії. Швидкість човна в стоячій воді дорівнює 24 км/год. Знайдіть швидкість течії, якщо проти течії турист і туристка проплили на 23 км більше, ніж за течією.
117.• Під час розселення туристів у намети виявилося, що коли в кожний намет поселити 6 туристів, то 5 туристам місця не вистачить, а якщо розселяти по 7 туристів, то 6 місць залишаться вільними. Скільки було туристів?
118.• Під час підготовки новорічних подарунків для учнів і учениць 7 класу виявилося, що коли в кожний подарунок покласти по 4 апельсини, то не вистачить 3 апельсинів, а коли покласти по 3 апельсини, то залишаться зайвими 25 апельсинів. Скільки було апельсинів?
119.•• У двох ящиках було 55 кг печива. Коли з першого ящика переклали в другий ![]() маси печива, яке в ньому містилося, то в першому ящику залишилося на 5 кг більше печива, ніж стало в другому. Скільки кілограмів печива було в кожному ящику спочатку?
маси печива, яке в ньому містилося, то в першому ящику залишилося на 5 кг більше печива, ніж стало в другому. Скільки кілограмів печива було в кожному ящику спочатку?
120.•• У двох кошиках було 24 кг груш. Коли з одного кошика переклали в другий ![]() маси груш, які були в першому, то маса груш у другому кошику стала вдвічі більшою за масу груш, які залишилися в першому. Скільки кілограмів груш було в кожному кошику спочатку?
маси груш, які були в першому, то маса груш у другому кошику стала вдвічі більшою за масу груш, які залишилися в першому. Скільки кілограмів груш було в кожному кошику спочатку?
121.•• На трьох полицях стояли книжки. На першій полиці стояло ![]() усіх книжок, на другій — 60 % усіх книжок, а на третій — на 8 книжок менше, ніж на першій. Скільки всього книжок стояло на трьох полицях?
усіх книжок, на другій — 60 % усіх книжок, а на третій — на 8 книжок менше, ніж на першій. Скільки всього книжок стояло на трьох полицях?
122.•• У чотири бідони розлили молоко. У перший бідон налили 30 % усього молока, у другий — ![]() того, що в перший, у третій — на 26 л менше, ніж у перший, а в четвертий — на 10 л більше, ніж у другий. Скільки літрів молока розлили в чотири бідони?
того, що в перший, у третій — на 26 л менше, ніж у перший, а в четвертий — на 10 л більше, ніж у другий. Скільки літрів молока розлили в чотири бідони?
123.•• Робітник планував щодня виготовляти по 20 деталей, щоб вчасно виконати виробниче завдання. Проте щодня він виготовляв на 8 деталей більше, ніж планував, і вже за 2 дні до кінця терміну роботи виготовив 8 деталей понад план. Скільки днів за планом робітник мав виконувати завдання?
124.•• Готуючись до екзамену, Олеся планувала щодня розв’язувати 10 задач. Оскільки вона щодня розв’язувала на 4 задачі більше, то вже за 3 дні до екзамену їй залишилося розв’язати 2 задачі. Скільки всього задач планувала розв’язати Олеся?
125.•• У двоцифровому числі кількість десятків у 3 рази більша за кількість одиниць. Якщо цифри числа переставити, то отримане число буде на 54 меншим від даного. Знайдіть дане двоцифрове число.
126.•• У двоцифровому числі кількість десятків на 2 менша від кількості одиниць. Якщо цифри числа переставити, то отримане число буде в 1![]() раза більшим за дане. Знайдіть дане двоцифрове число.
раза більшим за дане. Знайдіть дане двоцифрове число.
127.•• Із двох міст, відстань між якими дорівнює 270 км, виїхали одночасно назустріч один одному два автомобілі. Через 2 год після початку руху відстань між ними становила 30 км. Знай- діть швидкість кожного автомобіля, якщо швидкість одного з них на 10 км/год більша за швидкість другого.
128.•• Компанія складається із 7 осіб. Чи може кожна особа компанії дружити: 1) рівно з чотирма особами; 2) рівно з п’ятьма
особами?
129.•• Маємо два сплави міді й цинку. Перший сплав містить 9 % цинку, а другий — 30 %. Скільки кілограмів кожного сплаву треба взяти, щоб отримати зливок сплаву масою 300 кг, який містить 23 % цинку?
130.•• Маємо два водно-сольових розчини. Перший розчин містить 25 % солі, а другий — 40 %. Скільки кілограмів кожного розчину треба взяти, щоб отримати розчин масою 50 кг, який містить 34 % солі?
131.* У регіоні країни є 8 міст. Чи можна стверджувати, що з будьякого міста можна проїхати в будь-яке інше місто, якщо з кожного міста виходить: 1) не менше трьох доріг; 2) чотири дороги?
![]()
132. Обчисліть значення виразу:
1) –9,6 : 12 – 29 : (–5,8) + 4 : (–25);2) 3,4æ(4 4,6) 12,4æ( 0,8 2,2);
3) 0,4 ![]() æ6
æ6 ![]() 1,75 : 7
1,75 : 7 ![]() ;
;
4) 6,3 : ![]() 2,6 :
2,6 : ![]() æ
æ ![]() 0,6 : ( 0,36).
0,6 : ( 0,36).
133. Знайдіть значення виразу:
1) 14 – 6x, якщо x = 4; –2; 0; –0,3; ![]() ;
;
2) a2 + 3, якщо a = 7; –2; 0; 0,4; −1![]() ;
;
3) (2m – 1) n, якщо m = 0,2, n = –0,6.
134. Заповніть таблицю, обчислюючи значення виразу –3x + 2 для наведених значень x:
|
x |
–4 |
–3 |
–2 |
–1 |
0 |
1 |
2 |
3 |
4 |
|
–3x + 2 |
|
|
|
|
|
|
|
|
|
135. Яку цифру треба дописати ліворуч і праворуч до числа 37, щоб отримане число ділилося націло на 6?
136. Чи має корені рівняння:
1) x2 = 0; 3) | x | = x; 2) x2 = –1; 4) | x | = –x?
У разі ствердної відповіді вкажіть їх.
137. Чи може бути цілим числом значення виразу:
 1) ; 2) x ?
1) ; 2) x ?
138. Знайдіть усі натуральні значення n, при яких значення кожного з виразів n – 2, n + 24, n + 26 є простим числом.
завдання № 1 «Перевірте себе» в тестовій формі
![]()
ЗАВДАННЯ № 1 «ПЕРЕВІРТЕ СЕБЕ» В ТЕСТОВІЙ ФОРМІ
1. Обчисліть значення виразу 5 – 4b при b = –2.
А) 3; Б) –3; В) 13; Г) –13.
2. Знайдіть значення виразу ![]() m +
m + ![]() n, якщо m = 35, n = –18.
n, якщо m = 35, n = –18.
А) 1; Б) 2; В) 3; Г) 4.
3. Який із наведених виразів є записом різниці добутку чисел a і b та числа c?
А) a – bc; Б) ab – c; В) a (b – c); Г) (a – b) c.
4. Серед наведених алгебраїчних виразів укажіть цілий.
А) b ; Б) b 5; В) b+5; Г) b+5. b−7 b 7 7 b
5. Знайдіть корінь рівняння 7x + 2 = 3x – 6.
А) 2; Б) 1; В) –2; Г) –1.
6. Яке з рівнянь є лінійним?
А) 2x + 3 = 0; Б) 1 = 0; В) | x | – 4 = 0; Г) (x – 1) (x – 2) = 0. x
7. Розв’яжіть рівняння x x 6.
2 3
А) 12; Б) 36; В) –6; Г) –1.
8. Розв’яжіть рівняння 2 (x – 3) – (x + 4) = x – 10.
А) 0; В) x — будь-яке число;
Б) коренів немає; Г) 10.
9. При якому значенні a рівняння (a + 4) x = a – 3 не має коренів?
А) 3; Б) –4; В) 0; Г) такого значення не існує.
10. Відомо, що 45 % числа a на 7 більше, ніж ![]() цього числа. Знайдіть число a.
цього числа. Знайдіть число a.
А) 36; Б) 45; В) 60; Г) 90.
11. Три робітники виготовили 70 деталей. Перший робітник ви-готовив у 2 рази менше деталей, ніж другий, а третій — на 10 деталей більше, ніж перший.
Нехай перший робітник виготовив x деталей. Яке з наведених рівнянь відповідає умові задачі?
А) x + 2x + 2x + 10 = 70; В) x + 2x + 2x – 10 = 70;
Б) x + 2x + x + 10 = 70; Г) x + 2x + x – 10 = 70.
12. На першій ділянці було в 4 рази більше кущів малини, ніж на другій. Коли з першої ділянки пересадили на другу 12 кущів, то на другій стало у 2 рази менше кущів малини, ніж на першій. Нехай на другій ділянці було спочатку x кущів. Яке з наведених рівнянь є математичною моделлю ситуації, описаної в умові задачі?
|
А) 2 (4x – 12) = x + 12; |
В) 4x + 12 = 2 (x – 12); |
|
Б) 2 (4x + 12) = x – 12; |
Г) 4x – 12 = 2 (x + 12). |
ГОЛОВНЕ В ПАРАГРАФІ 1
Вираз зі змінними
Запис, складений із чисел, букв, знаків арифметичних дій і дужок, називають буквеним виразом або виразом зі змінними.
Алгебраїчні вирази
1) Числові вирази.
2) Вирази зі змінними (буквені вирази).
Цілий вираз
Вираз, який не містить ділення на вираз зі змінними, називають цілим виразом.
Лінійне рівняння з однією змінною
Рівняння виду ax = b, де x — змінна, a і b — деякі числа, називають лінійним рівнянням з однією змінною.
Алгоритм розв’язування задач на складання рівнянь
1) За умовою задачі скласти рівняння (побудувати математичну модель задачі);
2) розв’язати отримане рівняння;
3) з’ясувати, чи відповідає знайдений корінь змісту задачі, і дати відповідь.
Розв’язування лінійного рівняння з однією змінною
|
Значення a і b |
a ≠ 0 |
a = 0, b = 0 |
a = 0, b ≠ 0 |
|
Корені рівняння ax = b |
x = b a |
x — будь-яке число |
Коренів немає |
§ 2 ЦІЛІ ВИРАЗИ
•  У цьому параграфі ви навчитеся спрощувати вирази, ознайомитеся з формулами та прийомами, які допомагають полегшити роботу з перетворення виразів.
У цьому параграфі ви навчитеся спрощувати вирази, ознайомитеся з формулами та прийомами, які допомагають полегшити роботу з перетворення виразів.
• Ви дізнаєтеся, що піднесення числа до квадрата й куба — окремі випадки нової арифметичної дії.
• Ви навчитеся класифікувати алгебраїчні вирази.
4. Тотожно рівні вирази. Тотожності
Розглянемо дві пари виразів:
1) x5 – x і 5x3 – 5x; 2) 2 (x – 1) – 1 і 2x – 3.
У таблицях наведено значення цих виразів при деяких значеннях змінної x.
|
x |
–2 |
–1 |
0 |
1 |
2 |
|||||
|
x5 – x |
–30 |
0 |
0 |
0 |
30 |
|||||
|
5x3 – 5x |
–30 |
0 |
0 |
0 |
30 |
|||||
|
x |
–2 |
–1 |
0 |
1 |
2 |
|||||
|
2 (x – 1) – 1 |
–7 |
–5 |
–3 |
–1 |
1 |
|||||
|
2x – 3 |
–7 |
–5 |
–3 |
–1 |
1 |
|||||
Бачимо, що ці значення збігаються для кожної окремо взятої пари виразів.
Чи збережеться підмічена закономірність при будь-яких інших значеннях x?
Для виразів, записаних у першій таблиці, відповідь на це запитання заперечна: якщо, наприклад, x = 3, то x5 – x = 35 – 3 = 240, а 5x 3 5x 5æ33 5æ3 120.
Проте значення виразів, записаних у другій таблиці, збігаються при будь-яких значеннях x. Доведемо це.
2 (x – 1) – 1 = 2x – 2 – 1 = 2x – 3, тобто після спрощення вираз 2 (x – 1) – 1 перетворився у вираз 2x – 3.
Означення. Вирази, відповідні значення яких є рівними при будь-яких значеннях змінних, що входять до них, називають тотожно рівними.
Наприклад, вирази 2 (x – 1) – 1 і 2x – 3 — тотожно рівні, а вирази x5 – x і 5x3 – 5x не є тотожно рівними. Ось ще приклади тотожно рівних виразів:
7 (a + b) і 7a + 7b;
3x + y і y + 3x; m2np і nm2p; a – (b + c) і a – b – c.
Розглянемо рівність 7 (a + b) = 7a + 7b. Згідно з розподільною властивістю множення відносно додавання вона є правильною при будь-яких значеннях змінних a і b.
Означення. Рівність, яка є правильною при будь-яких значеннях змінних, що входять до неї, називають тотожністю.
З пари тотожно рівних виразів легко отримати тотожність.
Наприклад, усі рівності
3x + y = y + 3x, m2np = nm2p, a – (b + c) = a – b – c
є тотожностями.
Зазначимо, що з тотожностями ви стикалися й раніше. Так, рівності, що виражають властивості додавання та множення чисел, є прикладами тотожностей: a + b = b + a;
(a + b) + c = a + (b + c); ab = ba;
(ab) c = a (bc); a (b + c) = ab + ac.
Знайдемо значення виразу 11a – 3a + 2 при a = ![]() . Звичайно, можна відразу підставити в цей вираз замість a число
. Звичайно, можна відразу підставити в цей вираз замість a число ![]() та знайти значення числового виразу 11æ
та знайти значення числового виразу 11æ![]() 3æ
3æ![]() 2. Однак набагато зручніше спочатку звести подібні доданки, замінивши даний вираз 11a – 3a + 2 на тотожно рівний: 8a + 2. Тепер знайдемо значення отриманого виразу при a =
2. Однак набагато зручніше спочатку звести подібні доданки, замінивши даний вираз 11a – 3a + 2 на тотожно рівний: 8a + 2. Тепер знайдемо значення отриманого виразу при a = ![]() . Маємо: 8æ
. Маємо: 8æ![]() 2 3.
2 3.
4. Тотожно рівні вирази. Тотожності
Заміну одного виразу іншим, тотожно рівним йому, називають тотожним перетворенням виразу.
Зведення подібних доданків і розкриття дужок — приклади тотожних перетворень виразів. Спрощуючи вираз, ми фактично заміняємо його простішим, тотожно рівним йому.
Для того щоб довести, що дана рівність є тотожністю (або, як ще говорять, довести тотожність), використовують такі прийоми
(методи):
• тотожно перетворюють одну із частин даної рівності, отримуючи другу частину;
• тотожно перетворюють кожну із частин даної рівності, отримуючи один і той самий вираз;
• показують, що різниця лівої і правої частин даної рівності тотожно дорівнює нулю.
![]() ПРИКЛАД 1 Доведіть тотожність:
ПРИКЛАД 1 Доведіть тотожність:
1) 2 (3a + 4b) + 3 (a – 7b) – 7 (2a – 7b) = –5a + 36b; 2) 0,6 (x – 5) + 0,4 (x + 1) = 0,8 (x + 2) + 0,2 (x – 21); 3) a (b – c) + b (c – a) = c (b – a).
Розв’язання. 1) Спростимо ліву частину рівності:
2 (3a + 4b) + 3 (a – 7b) – 7 (2a – 7b) =
= 6a + 8b + 3a – 21b – 14a + 49b = –5a + 36b.
Тотожність доведено.
2) Спростимо ліву та праву частини рівності:
0,6 (x – 5) + 0,4 (x + 1) = 0,6x – 3 + 0,4x + 0,4 = x – 2,6;
0,8 (x + 2) + 0,2 (x – 21) = 0,8x + 1,6 + 0,2x – 4,2 = x – 2,6.
Отримали один і той самий вираз. Отже, тотожність доведено. 3) Розглянемо різницю лівої і правої частин рівності:
![]() a (b – c) + b (c – a) – c (b – a) = ab – ac + bc – ab – bc + ac = 0. Тотожність доведено.
a (b – c) + b (c – a) – c (b – a) = ab – ac + bc – ab – bc + ac = 0. Тотожність доведено. ¤
![]() ПРИКЛАД 2 Доведіть, що рівність (a + 2) (a – 3) = a2 – 6 не є тотожністю.
ПРИКЛАД 2 Доведіть, що рівність (a + 2) (a – 3) = a2 – 6 не є тотожністю.
Розв’язання. Щоб довести, що рівність не є тотожністю, достатньо навести контрприклад: указати таке значення змінної (змінних, якщо їх кілька), при якому дана рівність не справджується.
Наприклад, при a = 1 маємо:
![]() (a + 2) (a – 3) = (1 + 2) (1 – 3) = –6; a2 – 6 = 1 – 6 = –5. Отже, дана рівність не є тотожністю.
(a + 2) (a – 3) = (1 + 2) (1 – 3) = –6; a2 – 6 = 1 – 6 = –5. Отже, дана рівність не є тотожністю. ¤
1. Які вирази називають тотожно рівними?
2. Що називають тотожністю?
3. Що називають тотожним перетворенням виразу?
4. Які тотожні перетворення виразів ви знаєте?
5.  Які прийоми використовують для доведення тотожностей?
Які прийоми використовують для доведення тотожностей?
ВПРАВИ
139.° Які властивості арифметичних дій дають можливість стверджувати, що дані вирази є тотожно рівними:
|
1) ab + cd і cd + ab; |
4) (x + 2) (x + 3) і (3 + x) (2 + x); |
|
2) (a + 1) + b і a + (1 + b); 3) aæ4b і 4ab; 140.° Чи є тотожністю рівність: |
5) 7 (a – 4) і 7a – 28? |
|
1) 2x – 12 = 2 (x – 6); |
7) 3a – a = 3; |
|
2) a – b = –(b – a); |
8) 4x + 3x = 7x; |
|
3) 3m + 9 = 3 (m + 9); |
9) a – (b + c) = a – b + c; |
|
4) (a b)æ1 a b; |
10) m + (n – k) = m + n – k; |
|
5) (a b)æ0 a b; |
11) 4a – (3a – 5) = a + 5; |
|
6) (a – a) (b + b) = 0; |
12) (a – 5) (a + 3) = (5 – a) (3 + a)? |
141.° Чи є тотожно рівними вирази:
1) 8 (a – b + c) і 8a – 8b + 8c; 3) (5a – 4) – (2a – 7) і 3a – 11? 2) –2 (x – 4) і –2x – 8;
142.° Порівняйте значення виразів a2 і | a | при a = –1; 0; 1. Чи можна стверджувати, що рівність a2 = | a | є тотожністю?
143.° Якому з наведених виразів тотожно дорівнює вираз –3a + + 8b – a – 11b:
1) –4a + 3b; 2) –3a + 3b; 3) –4a – 3b; 4) –3a – 3b?
144.° Серед виразів –10a + 7, –10a – 7, –14a + 7, –14a – 7 знайдіть такий, який тотожно дорівнює виразу –12a + (7 – 2a).
145.° Доведіть тотожність:
1) –5x – 6 (9 – 2x) = 7x – 54;
2) ![]() (12 0,6y) 0,3y 0,1y 4;
(12 0,6y) 0,3y 0,1y 4;
3) 3 (7 – a) – 7 (1 – 3a) = 14 + 18a;
4) (6x – 8) – 5x – (4 – 9x) = 10x – 12; 5) 3 (2,1m – n) – 0,9 (7m + 2n) = –4,8n;
6) ![]() x 6
x 6 ![]() 24 1
24 1![]() x 0.
x 0.
4. Тотожно рівні вирази. Тотожності
146.° Доведіть тотожність:
1) –0,2 (4b – 9) + 1,4b = 0,6b + 1,8;
2) (5a – 3b) – (4 + 5a – 3b) = –4;
3) 5 (0,4x – 0,3) + (0,8 – 0,6x) = 1,4x – 0,7;
4) ![]() (3y 27) 2
(3y 27) 2 ![]() y 1,5
y 1,5 ![]() y.
y.
147.• Які з наведених рівностей є тотожностями:
1) (2a – 3b)2 = (3b – 2a)2; 5) | a2 + 4 | = a2 + 4;
2) (a – b)3 = (b – a)3; 6) | a + b | = | a | + | b |;
3) | a + 5 | = a + 5; 7) | a – 1 | = | a | – 1; 4) | a – b | = | b – a |; 8) a2 – b2 = (a – b)2?
148.• Запишіть у вигляді рівності твердження:
1) сума протилежних чисел дорівнює нулю;
2) добуток даного числа та числа 1 дорівнює 1;
3) добутком даного числа та числа –1 є число, протилежне даному;
4) модулі протилежних чисел рівні;
5) різниця протилежних чисел дорівнює нулю.Які із цих рівностей є тотожностями?
149.• Доведіть тотожність:
1) 4 (2 – 3m) – (6 – m) – 2 (3m + 4) = –17m – 6; 2) a + b – 10ab = 2a (3 – b) – 3b (a – 2) – 5 (ab + a + b); 3) 6 (5a – 3) + (10 – 20a) – (6a – 4) = 5a – (3a – (2a – 4)).
150.• Доведіть тотожність:
1) (3m 7)æ0,6 0,8 (4m 5) ( 1,7 1,4m) 1,5; 2) 7a (3b 4c) 3a b ![]() c 9a (2b 3c).
c 9a (2b 3c).
151.• Доведіть, що не є тотожністю рівність:
1) (a + 3)2 = a2 + 9; 3) (c + 1)3 = c3 + 1;
2) (b – 1) (b + 1) = (b – 1) b + 1; 4) | m | – | n | = | n | – | m |.
152.• Доведіть, що не є тотожно рівними вирази:
1) 4 – m2 і (2 – m)2; 3) m3 + 8 і (m + 2) (m2 + 4).
2) | –m | і m;
![]()
153. Пасажирський поїзд проходить відстань між двома станціями за 12 год. Якщо одночасно від цих станцій вирушать назустріч один одному пасажирський і товарний поїзди, то вони зустрінуться через 8 год після початку руху. За який час товарний поїзд може подолати відстань між цими станціями?
¿ 154. У багатьох країнах світу, зокрема в Україні, температуру вимірюють за шкалою Цельсія[1]. У деяких країнах, зокрема в США, температуру вимірюють за шкалою Фаренгейта[2]. Щоб перевести значення температури за шкалою Цельсія в шкалу Фаренгейта, користуються формулою tF = 1,8tC + 32, де tC — температура в градусах Цельсія, tF — температура в градусах Фаренгейта. Скільком градусам за шкалою Цельсія відповідають 68 градусів за
![]()
![]() шкалою Фаренгейта?°C °F
шкалою Фаренгейта?°C °F
155. Відомо, що a > 0 і a + b < 0. Порівняйте:
1) b і 0; 2) | a | і | b |.
156. Ціну товару спочатку збільшили на 50 %, а потім зменшили на 50 %. Збільшилася чи зменшилася початкова ціна товару та на скільки відсотків?
157. Загальна довжина річки Дніпро становить 2201 км, з них у межах України — 981 км. Загальна довжина річки Десна становить 1130 км, з них у межах України — 591 км. Яка із цих річок має більший відсоток довжини в межах України?
 УЧИМОСЯ РОБИТИ НЕСТАНДАРТНІ КРОКИ
УЧИМОСЯ РОБИТИ НЕСТАНДАРТНІ КРОКИ
158. На дошці записано числа 1, 2, 3, ..., 10. За один крок дозволено вибрати два числа, до кожного з них додати 5 або від кожного відняти 1. Чи можна за допомогою цих операцій домогтися того, щоб усі числа, записані на дошці, виявилися рівними?
 5. Степінь з натуральним показником
5. Степінь з натуральним показником
Як ви знаєте, у математиці придумали спосіб коротко записувати добуток, усі множники якого рівні.
3
Наприклад, ![]() æ
æ![]() æ
æ![]() .
.
3
Вираз ![]() називають степенем, число
називають степенем, число ![]() — основою степеня, а число 3 — показником степеня.
— основою степеня, а число 3 — показником степеня.
Означення. Степенем числа a з натуральним показником n, більшим за 1, називають добуток n множників, кожний з яких дорівнює a.
Степінь з основою a та показником n записують an і читають: «a в n-му степені». Степені з показниками 2 і 3 можна прочитати інакше: запис a2 читають «a у квадраті», запис a3 — «a в кубі».
Звернемо увагу, що в означенні степеня на показник n накладено обмеження n > 1. І це зрозуміло: адже не прийнято розглядати добуток, що складається з одного множника.
А чи може показник степеня дорівнювати 1? Відповідь на це запитання дає таке означення.
Означення. Степенем числа a з показником 1 називають саме це число.
Таке означення дає змогу будь-яке число вважати степенем з показником 1.
Отже, з наведених означень випливає, що
an = aaæ...æa, де n > 1,
n множ ник ів a1 = a.
Легко підрахувати, що, наприклад, 25 = 32. У таких випадках говорять, що число 2 піднесли до п’ятого степеня й отримали число 32. Також можна сказати, що виконали дію піднесення до п’ятого степеня числа 2.
Рівність (–3)2 = 9 означає, що число –3 піднесли до квадрата й отримали число 9, а рівність (–3)3 = –27 означає, що число –3 піднесли до куба й отримали число –27.
Зауважимо, що алгебраїчний вираз може бути побудований не тільки за допомогою додавання, віднімання, множення та ділення, а й за допомогою дії піднесення до степеня.
Очевидно, що коли a > 0, то an > 0; коли a = 0, то 0n = 0.
Отже, підносячи невід’ємне число до степеня, отримуємо невід’ємне число.
При піднесенні від’ємного числа до степеня можливі два випадки.
1) Якщо показник степеня — парне число, то при піднесенні до степеня множники можна розбити на пари.
Наприклад, (–2)6 = ((–2) (–2))æ((–2) (–2))æ((–2) (–2)).
2) Якщо показник степеня — непарне число, то один множник залишиться без пари.
Наприклад, (–2)5 = ((–2) (–2))æ((–2) (–2))æ(–2).
Оскільки кожні два від’ємні множники дають у добутку додатне число, то справедливе таке твердження:
підносячи від’ємне число до степеня з парним показником, отримуємо додатне число, а підносячи від’ємне число до степеня з непарним показником, отримуємо від’ємне число.
Чи можна, наприклад, число 5 піднести до степеня 0 або до степеня –2? Можна. Як це зробити, ви дізнаєтесь із курсу алгебри 8 класу.
![]() ПРИКЛАД 1 Розв’яжіть рівняння (x – 10)8 = –1.
ПРИКЛАД 1 Розв’яжіть рівняння (x – 10)8 = –1.
Розв’язання. Оскільки при піднесенні до степеня з парним показником будь-якого числа отримуємо невід’ємне число, то дане рівняння не має коренів.
![]() Відповідь: коренів немає.
Відповідь: коренів немає. ¤
![]() ПРИКЛАД 2 Доведіть, що значення виразу 10200 + 2 ділиться націло на 3.
ПРИКЛАД 2 Доведіть, що значення виразу 10200 + 2 ділиться націло на 3.
![]() Розв’язання. Запис значення виразу 10200 складається із цифри 1 і двохсот цифр 0, а запис значення виразу 10200 + 2 — із цифри 1, цифри 2 і ста дев’яноста дев’яти цифр 0. Отже, сума цифр числа, яка є значенням даного виразу, дорівнює 3. Тому й саме це число ділиться націло на 3.
Розв’язання. Запис значення виразу 10200 складається із цифри 1 і двохсот цифр 0, а запис значення виразу 10200 + 2 — із цифри 1, цифри 2 і ста дев’яноста дев’яти цифр 0. Отже, сума цифр числа, яка є значенням даного виразу, дорівнює 3. Тому й саме це число ділиться націло на 3. ¤
|
Розв’язання. Якщо n — парне число, то вираз 9n можна подати у вигляді добутку, який містить парну кількість дев’яток. Тоді можна записати: 9n = (9æ9) (9æ9) ... (9æ9). Оскільки 9æ9 = 81, то останньою цифрою значення виразу (9æ9) (9æ9) ... (9æ9) є одиниця.
|
1. Що називають степенем числа a з натуральним показником n, більшим за 1?
2. Як читають запис an? a2? a3?
3. Що називають степенем числа a з показником 1?
4. Чому дорівнює значення виразу 0n при будьякому натуральному значенні n?
5. Яке число, додатне чи від’ємне, отримують при піднесенні до степеня додатного числа?
6.  Яким числом, додатним чи від’ємним, є значення степеня від’ємного числа, якщо показник степеня є парним числом? непарним числом?
Яким числом, додатним чи від’ємним, є значення степеня від’ємного числа, якщо показник степеня є парним числом? непарним числом?
ВПРАВИ
159.° Прочитайте вираз, назвіть основу та показник степеня:
1) 96; 3) 0,35; 5) (–0,6)3; 7) 731; 2) 2,47; 4) (–8)2; 6) (–a)11; 8) (3p)12.
160.° Спростіть вираз, замінивши добуток однакових множників степенем:
|
1) 5æ5æ5æ5; |
5) x 2æx 2æx 2æx 2; |
|
2) (−7)æ(−7)æ(−7); |
6) yæyæ...æy; 10 множ ник ів |
|
3) aæaæaæaæa; |
7) 0,4æ0,4æ...æ0,4; |
k множ ник ів
4) 2mæ2mæ2mæ2mæ2m ; 8) cæcæ...æc.
m множ ник ів 161.° Подайте у вигляді степеня добуток:
1) c c c c c c c cæ æ æ æ æ æ æ ; 3) (−x )æ(−x ) ... (æ æ −x);
19 множників
2) 5bæ æ5b 5b; 4) (a b+ )æ(a b+ ) ... (æ æ a b+ ).
d множ ників
162.° Користуючись означенням степеня, подайте у вигляді добутку степінь:
2
1) 116; 3) ![]() ; 5) (–3,6)7;
; 5) (–3,6)7;
2) 0,14; 4) (5c)3; 6) (a + b)5.
163.° Користуючись означенням степеня, подайте у вигляді добутку степінь:
4
1) 37; 2) 2 1 ; 3) (c + d)3; 4) (a – b)2.
7
164.° Чому дорівнює значення виразу:
1) 0,62; 3) (–9)2; 5) (–1)12;
2 2
2) 06; 4) 112; 6) ?
3
165.° Знайдіть значення виразу:
3 4
1) 83; 3) (–1,9)2; 5) ; 7) (–0,01)3;
4
![]() 1 35
1 35
2) 1,53; 4) ; 6) (–0,6)3; 8) 1.
9
166.° Виконайте піднесення до степеня:
6
1) 72; 3) 1,22; 5) (–0,8)3; 7) ![]() ;
;
43
2) 0,53; 4) (–1)7; 6) ![]() ; 8) 3
; 8) 3![]() .
.
167.° Заповніть таблицю:
|
a |
2 |
–2 |
10 |
–10 |
0,1 |
–0,1 |
|
− |
|
a2 |
|
|
|
|
|
|
|
|
|
a3 |
|
|
|
|
|
|
|
|
|
a4 |
|
|
|
|
|
|
|
|
168.° Заповніть таблицю:
|
a |
–6 |
6 |
–0,4 |
0,4 |
3 |
0,03 |
|
–1 |
0 |
|
10a2 |
|
|
|
|
|
|
|
|
|
|
(10a)2 |
|
|
|
|
|
|
|
|
|
169.° Площа Кримського півострова — найбільшого півострова України — дорівнює 2,55æ10 4 км2. Виразіть цю площу натуральним числом у квадратних кілометрах.
170.° Відстань від Землі до Сонця дорівнює 1,495æ1011 м. Виразіть цю відстань натуральним числом у метрах.
171.° Площа материків і островів Землі становить 1,49æ10 8 км2, а площа океанів — 3,61æ10 8 км2. Виразіть ці площі натуральними числами у квадратних кілометрах.
|
172.° Обчисліть: |
|
|
1) 82 – 110; |
3) (4,2 −3,8)4æ252; |
|
2) 0,3æ24; 173.° Обчисліть: |
4) (63 : 200 – 0,42) : 0,23. |
1) 43 + 35; 2) 0,63 – 0,43; 3) 0,12æ54.
174.° Знайдіть значення виразу:
1) x2 – x3, якщо x = 0,1;
2) 15a2, якщо a = 0,4;
3) (x – y)5, якщо x = 0,8, y = 0,6;
4) a2b3, якщо a = 0,6, b = 0,5;
5) (x2 – y2) : (x – y), якщо x = 5, y = 3;
6) (x2 – y2) : x – y, якщо x = 5, y = 3;
7) x2 – y2 : (x – y), якщо x = 5, y = 3; 8) x2 – y2 : x – y, якщо x = 5, y = 3.
175.° Знайдіть значення виразу: 1) 16 – c3, якщо c = 2;
2) (16x)6, якщо x = 0,125; 3) a3b2, якщо a = 10, b = 0,1; 4) 4a4 – a, якщо a = 3.
176.° Не виконуючи обчислення, порівняйте:
1) (–5,8)2 і 0; 4) –88 і (–8)8;
2) 0 і (–3,7)3; 5) (–17)6 і 176; 3) (–12)7 і (–6)4; 6) (–34)5 і (–39)5.
177.° Не виконуючи обчислення, порівняйте: 1) 0 і (–1,9)10; 3) (–0,1)12 і (–12)25;
99
2) 0 і (–76)15; 4) 4 ![]() і 5
і 5![]() .
.
178.° Порівняйте з нулем значення виразів: 2100; (–2)100; –2100; –(–2)100. Чи є серед цих виразів такі, що набувають рівних значень?
179.° Порівняйте з нулем значення виразів: 5101; –5101; (–5)101; –(–5)101. Чи є серед цих виразів такі, що набувають рівних значень?
180.° Чи є правильною рівність:
1) 32 + 42 = 72;
2) 52 + 122 = 132;
3) 12 + 32 + 52 + 72 + 92 = 132; 4) (1 + 2 + 3)2 = 13 + 23 + 33?
181.° Доведіть, що 12 + 22 + 42 + 62 + 82 = 112.
182.• Розташуйте в порядку зростання значення виразів:
1) 0,3; 0,32; 0,33; 2) –0,4; (–0,4)2; (–0,4)3.
183.• Порівняйте з нулем значення виразу:
1) (−4)7 æ(−12)9; 2) (−5)6æ(−17)11; 3) (−14)4æ(−25)14; 4) (−7)9æ06.
184.• Порівняйте з нулем значення виразу:
1) (−2)14æ(−3)15æ(−4)16; 2) (−5)17 æ(−6)18æ(−7)19.
185.• Запишіть:
1) числа 16; 64; 256 у вигляді степеня з основою 4;
2) числа 0,09; 0,027; 0,00243 у вигляді степеня з основою 0,3.
186.• Подайте число: 1) 10 000; 2) –32; 3) 0,125; 4) –0,00001; 5) −![]() у вигляді степеня з показником, більшим за 1, і з найменшою за модулем основою.
у вигляді степеня з показником, більшим за 1, і з найменшою за модулем основою.
187.• Складіть числовий вираз і знайдіть його значення:
1) квадрат різниці чисел 7 і 5;
2) різниця квадратів чисел 7 і 5; 3) куб суми чисел 4 і 3;
4) сума кубів чисел 4 і 3.
188.• Складіть числовий вираз і знайдіть його значення:
1) сума куба числа 5 і квадрата числа 8;
2) куб різниці чисел 9 і 8; 3) сума квадратів чисел 2,5 і 0,25; 4) квадрат суми чисел 7,8 і 8,2.
189.• Скільки в 1 км міститься:
1) метрів; 2) сантиметрів; 3) міліметрів?
Відповідь запишіть у вигляді степеня числа 10.
190.• Яке число треба підставити замість зірочки, щоб утворилася правильна рівність:
1) 1 га = 10* а; 3) 1 а = 10* м2;
2) 1 га = 10* м2; 4) 1 га = 10* см2?
191.• Швидкість світла у вакуумі дорівнює 300 000 км/с.
1) Запишіть цю величину, використовуючи степінь числа 10.
2) Виразіть швидкість світла в метрах за секунду; запишіть результат, використовуючи степінь числа 10.
192.• Скільки в 1 м2 міститься: 1) квадратних дециметрів;
2) квадратних сантиметрів; 3) квадратних міліметрів?
Відповідь запишіть у вигляді степеня числа 10.
193.• Які із чисел –3, –2, –1, 0, 1, 2, 3 є коренями рівняння:
1) x4 = 16; 3) x2 + x = 2;
2) x5 = –243; 4) x3 + x2 = 6x?
194.• При якому значенні x дорівнює нулю значення виразу:
1) (2x – 3)2; 2) (x + 4)4; 3) (6x – 1)5?
195.• Розв’яжіть рівняння:
1) x10 = –1; 2) (x – 5)4 = –16.
196.• При яких натуральних значеннях n є правильною нерівність 8 < 3n < 85?
197.• При яких натуральних значеннях m є правильною нерівність 0,07 < 0,4m < 0,5?
198.•• Доведіть, що вираз x2 + (x – 1)2 набуває лише додатних значень.
199.•• Доведіть, що вираз (x + 1)2 + | x | набуває лише додатних значень.
200.•• Доведіть, що не має додатних коренів рівняння:
1) 2x2 + 5x + 2 = 0; 2) x4 + 3x3 + 4x2 + 3x + 1 = 0.
201.•• Доведіть, що не має від’ємних коренів рівняння:
1) x4 – 5x3 + 6x2 – 7x + 5 = 0; 2) x8 + x4 + 1 = x7 + x3 + x.
202.•• При яких значеннях x і y є правильною рівність:
1) x2 + y2 = 0; 2) (x – 1)4 + (y + 2)6 = 0?
203.•• При яких значеннях x і y є правильною рівність x8 + (y – 3)2 = 0?
204.•• При якому значенні змінної набуває найменшого значення вираз:
1) x2 + 7; 2) (x – 1)4 + 16?
205.•• При якому значенні змінної набуває найбільшого значення вираз:
1) 10 – x2; 2) 24 – (x + 3)6?
206.•• Доведіть, що значення виразу:
1) 101101 + 103103 ділиться націло на 2;
2) 167 + 158 – 119 ділиться націло на 10;
3) 1010 – 7 ділиться націло на 3;
4) 6n – 1 ділиться націло на 5 при будь-якому натуральному значенні n.
207.•• Доведіть, що значення виразу:
1) 10100 + 8 ділиться націло на 9;
2) 111n – 6 ділиться націло на 5 при будь-якому натуральному значенні n.
![]()
208. Обчисліть значення виразу
3![]() æ1,3 7,2æ
æ1,3 7,2æ![]() 9,1: 3,5 :
9,1: 3,5 : ![]() .
.
209. Для кафе потрібно придбати 20 нових стільців у одного з трьох постачальників. Ціни стільців та умови доставки покупки наведено в таблиці.
|
Постачальник |
Ціна одного стільця, грн |
Вартість доставки, грн |
Додаткові умови |
|
А |
1200 |
2250 |
Відсутні |
|
Б |
1100 |
2500 |
Доставка безкоштовна, якщо сума замовлення перевищує 30 000 грн |
|
В |
1400 |
2000 |
Доставка безкоштовна, якщо сума замовлення перевищує 25 000 грн |
Скільки гривень треба заплатити за найдешевший варіант покупки з доставкою?
210. До зливку сплаву масою 400 кг, що містить 15 % міді, додали 25 кг міді. Яким став відсотковий вміст міді в новому зливку?
211. В одному мішку було 80 кг цукру, а в другому — 60 кг. З першого мішка взяли в 3 рази більше цукру, ніж із другого, після чого в другому мішку залишилося цукру у 2 рази більше, ніж у першому. Скільки кілограмів цукру взяли з кож- ного мішка?
212. Розв’яжіть рівняння:
1) 9 (2x – 1) – 5 (11 – x) = 3 (x + 4); 2) 5x – 26 = 12x – 7 (x – 4).
213. Відомо, що одне із чисел a, b і c додатне, друге — від’ємне, а третє дорівнює нулю, причому | a | = b2 (b – c). Установіть, яке із чисел є додатним, яке від’ємним і яке дорівнює нулю.
![]() ГОТУЄМОСЯ ДО ВИВЧЕННЯ НОВОЇ ТЕМИ
ГОТУЄМОСЯ ДО ВИВЧЕННЯ НОВОЇ ТЕМИ
214. Порівняйте значення виразів:
4 312
1) 22æ23 і 25; 4) ![]() і
і ![]() ;
;
|
2) 42æ41 і 43; |
5) 53æ23 і (5æ2)3; |
|
3) (33)2 і 36; |
6) (0,25æ4)2 і 0,25æ42. |
 УЧИМОСЯ РОБИТИ НЕСТАНДАРТНІ КРОКИ
УЧИМОСЯ РОБИТИ НЕСТАНДАРТНІ КРОКИ
215. У деякому місті від будь-якої станції метро можна доїхати до будь-якої іншої станції (можливо, з пересадками). Доведіть, що існує станція, яку можна закрити (без права проїзду через неї), і при цьому від будь-якої станції з тих, що залишилися, можна буде доїхати до будь-якої іншої.
 6. Властивості степеня з натуральним показником
6. Властивості степеня з натуральним показником
Розглянемо добуток двох степенів з однаковими основами, наприклад a2a5. Цей вираз можна подати у вигляді степеня з основою a: a 2a 5 = (aa)æ(aaaaa) = aaaaaaa = a7.
Отже, a 2a 5 a 2 5.
Аналогічно легко переконатися в тому, що, наприклад, a3æa2 = = a3+2 = a5, aæa 9 a1 9 a10.
Простежується закономірність: aman am n, де m і n — довільні натуральні числа.
Проте жодна кількість конкретних прикладів не може гарантувати, що наведена рівність є правильною для будь-яких натуральних чисел m і n. Істинність її можна встановити тільки шляхом доведення.
У математиці твердження, справедливість якого встановлено за допомогою доведення, називають теоремою.
Теорема 6.1. Для будь-якого числа a та будь-яких натуральних чисел m і n є справедливою рівність aman am n.
Доведення. Для m > 1 і n > 1 маємо:
aman (aaæ...æa) (aaæ...æa) aaæ...æa am n.
m множ ник ів n множ ник ів (m n) множ ник ів
Оскільки не прийнято розглядати добуток, що складається з одного множника, то для повноти доведення слід окремо розглянути випадки: m = 1 і n > 1; m > 1 і n = 1; m = n = 1. Так, якщо m = 1 і n > 1, то
aæan aæ(aaæ...æa) aaæ...æa an 1.
n множ ник ів (n 1) множ ник ів
Випадки, коли m > 1 і n = 1 або коли m = n = 1, розгляньте самостійно. p
Тотожність aman am n виражає основну властивість степеня.
Аналогічна властивість має місце й для добутку трьох і більше степенів. Наприклад,
32æ33æ37 (32æ33)æ37 32 3æ37 3(2 3) 7 32 3 7 312.
Отже,перемножуючи степені з однаковими основами, показники додають, а основу залишають тією самою.
Розглянемо вираз a9 : a4, де a ≠ 0. Він є часткою двох степенів з однаковими основами. Оскільки a 4æa 5 = a 9, то за означенням частки можна записати a9 : a4 = a5, тобто a9 : a4 = a 9 – 4. Цей приклад підказує, що має місце така теорема.
Теорема 6.2. Для будь-якого числа a, відмінного від нуля, і будь-яких натуральних чисел m і n таких, що m > n,є справедливою рівність
am : an =am – n.
Доведення. Розглянемо добуток степенів an і am – n. Використовуючи основну властивість степеня, маємо:
anæam n an (m n) an m n am.
Тоді за означенням частки:
am : an = am – n. p Із цієї теореми випливає таке правило:
при діленні степенів з однаковими основами від показника
степеня діленого віднімають показник степеня дільника, а основу залишають тією самою.
Розглянемо вираз (a3)4. Він є степенем з основою a3 і показником 4. Тому
(a 3)4 a 3a 3a 3a 3 a 3 3 3 3 a 3æ4 a12.
Цей приклад підказує, що має місце така теорема.
Теорема 6.3. Для будь-якого числа a та будь-яких натуральних чисел m і n є справедливою рівність
(am)n =amn.
Доведення. Очевидно, що для n = 1 рівність, яку треба довести, є пра вильною. Для n > 1 маємо:
n доданк ів
(am)n amamæ...æam am m ... m amn.p
n множ ник ів
Із цієї теореми випливає таке правило:
при піднесенні степеня до степеня показники перемножують, а основу залишають тією самою.
Наприклад, (37 )2 = 37æ2 =314, (x k)3 = x kæ3 = x 3k.
Покажемо, як можна перетворити степінь добутку, наприклад вираз (ab)3:
(ab)3 = (ab)æ(ab)æ(ab) = (aaa)æ(bbb) = a 3b3.
У загальному випадку має місце така теорема.
Теорема 6.4. Для будь-яких чисел a і b та будь-якого натурального числа n є справедливою рівність
(ab)n =anbn.
Доведення. Очевидно, що для n = 1 рівність, яку треба довести, є правильною. Для n > 1 маємо:
(ab)n = (ab)æ(ab)æ...æ(ab) = (aaæ...æa) ( bbæ...æb) = anbn. p
n множ ник ів n множ ник ів n множ ник ів
Аналогічна властивість має місце й для добутку трьох або більше множників. Наприклад, (abc)n = ((ab)æc)n = (ab)næcn = anbncn.
Отже, при піднесенні добутку до степеня кожний множник підносять до степеня й отримані результати перемножують.
![]() ПРИКЛАД 1 Спростіть вираз: 1) (a 5)2æ(a 6)7; 2) (–a4)9; 3) (–a4)8.
ПРИКЛАД 1 Спростіть вираз: 1) (a 5)2æ(a 6)7; 2) (–a4)9; 3) (–a4)8.
Розв’язання. 1) Застосувавши послідовно правило піднесення степеня до степеня та правило множення степенів з однаковою основою, отримаємо:
(a 5)2æ(a 6)7 = a10æa 42 = a 52.
2) Оскільки a 4 1æa 4, то, застосувавши правило піднесення добутку до степеня, отримаємо:
(–a4)9 = (–1æa4)9 = (–1)9æ(a4)9 = –1æa36 = –a36.
3) ![]() Маємо: ( a 4)8 ( 1æa 4)8 ( 1)8æ(a 4)8 1æa 32 a 32. ¤
Маємо: ( a 4)8 ( 1æa 4)8 ( 1)8æ(a 4)8 1æa 32 a 32. ¤
![]()
![]() ПРИКЛАД 2 Подайте у вигляді степеня вираз 216a3b6. Розв’язання. Маємо: 216a3b6 = 63æa 3æ(b2)3 = (6ab2)3. ¤
ПРИКЛАД 2 Подайте у вигляді степеня вираз 216a3b6. Розв’язання. Маємо: 216a3b6 = 63æa 3æ(b2)3 = (6ab2)3. ¤
7 9
![]() ПРИКЛАД 3 Знайдіть значення виразу 11 æ 3 .
ПРИКЛАД 3 Знайдіть значення виразу 11 æ 3 .
3 4
7 9 7 7 27 2 2
![]()
![]() Розв’язання. 11 æ 3 4 æ 3 æ 3æ3 æ 3 3 9 . ¤
Розв’язання. 11 æ 3 4 æ 3 æ 3æ3 æ 3 3 9 . ¤
3 4 3 4 44 4 4 16
![]() ПРИКЛАД 4 Порівняйте значення виразів:
ПРИКЛАД 4 Порівняйте значення виразів:
1) (–11)14æ(–11)3 і (–11)16; 3) 530 і 920;
2) (–12)19 і (–12)15; 4) 163 і 652.
Розв’язання. 1) Маємо: ( 11)14æ( 11)3 ( 11)17 . Зазначимо, що
(–11)17 < 0. Разом з тим (–11)16 > 0.
Отже, ( 11)14æ( 11)3 ( 11)16.
2) Оскільки | (–12)19 | > | (–12)15 |, а числа, які треба порівняти, від’ємні, то (–12)19 < (–12)15.
3) Оскільки 530 = (53)10 = 12510 і 920 = (92)10 = 8110, то 530 > 920.
4) ![]() Маємо: 163 = (42)3 = (43)2 = 642. Отже, 163 < 652. ¤
Маємо: 163 = (42)3 = (43)2 = 642. Отже, 163 < 652. ¤
![]() ПРИКЛАД 5 Якою цифрою закінчується значення виразу 2100?
ПРИКЛАД 5 Якою цифрою закінчується значення виразу 2100?
Розв’язання. Маємо: 2100 = (24)25 = 1625. Оскільки 6æ6 = 36, то добуток будь-яких чисел, що закінчуються на 6, є числом, остання цифра якого 6.
Тому коли число закінчується цифрою 6, то будь-який його степінь закінчується цифрою 6.

|
216.° Подайте у вигляді степеня добуток: |
|
|
1) m5m4; 5) y3y5y9; |
9) x4xx11x2; |
|
2) xx7; 6) c8c9c; |
10) (ab)5æ(ab)15; |
|
3) a3a3; 7) (b – c)10 (b – c)6; |
11) (2x +3y)6æ(2x +3y)14; |
|
4) 6 8æ63; 8) 112æ114æ116; 217.° Подайте у вигляді степеня вираз: |
12) (−xy)2æ(−xy)7 æ(−xy)9. |
|
1) a5a8; 3) a9a; |
5) (m +n)13æ(m +n); |
|
2) a2a2; 4) aa2a3; |
6) (cd)8æ(cd)18æ(cd). |
218.° Замініть зірочку таким степенем з основою a, щоб виконувалася рівність:
1) a 6æ* = a14; 2) *æa 6 = a7; 3) a10æ*æa 2 = a18.
219.° Подайте вираз a12 у вигляді добутку двох степенів з основами a, один з яких дорівнює:
1) a6; 2) a4; 3) a3; 4) a5; 5) a.
220.° Подайте у вигляді степеня частку:
1) a12 : a3; 3) c7 : c6; 2) b6 : b; 4) (a + b)8 : (a + b)4.
221.° Знайдіть значення виразу:
1) 77 : 75; 3) 0,69 : 0,66;
53
2) 1018 : 1014; 4) 1![]() : 1
: 1![]() .
.
222.° Виконайте ділення:
1) m10 : m2; 2) x5 : x4; 3) y18 : y6.
223.° Подайте у вигляді степеня з основою m вираз:
1) (m5)3; 2) (m3)4; 3) ((m2)4)6; 4) (m 7 )2æ(m 4)9.
224.° Подайте у вигляді степеня з основою n вираз:
1) (n2)8; 2) (n9)5; 3) ((n3)2)10; 4) (n 12)4æ(n 21)2.
225.° Подайте степінь у вигляді добутку степенів:
1) (ab)6; 3) (3c)7; 5) (–0,2cd)4;
9
2) (mnp)5; 4) (–8xy)3; 6) ![]() kt .
kt .
226.° Подайте степінь у вигляді добутку степенів:
1) (ax)2; 2) (xyz)12; 3) (7m)8; 4) (–0,3bc)11.
227.° Спростіть вираз:
1) −xæx 2; 3) −xæ(−x)2; 2) (−x)2æx ; 4) (−x)æ(−x)2æ(−x).
228.° Спростіть вираз:
1) (−a)2æa 3; 3) a 2æ(−a)3;
2) −a 2æa 3; 4) −a 2æ(−a)3.
229.° Спростіть вираз:
1) (–a5)2; 2) (–a3)3; 3) (−a 4)7 æ(−a 2)6.
230.° Спростіть вираз:
1) ((–a6)5)9; 2) ((–a11)2)3.
231.° Подайте у вигляді степеня вираз:
1) a3b3; 3) 9m2n2; 5) − 27 c3d 3;
343
2) –m7; 4) 64x3y3; 6) 0,0001k4p4.
232.° Подайте у вигляді степеня вираз:
1) x12y12; 3) 32p5q5;
2) –125m3n3; 4) 1 000 000 000a9b9c9.
233.° Подайте вираз у вигляді степеня та обчисліть його значення (у разі потреби скористайтеся таблицею степенів чисел 2 і 3, розміщеною на форзаці підручника):
9
1) 23æ24; 3) 0,2æ0,22æ0,23; 5) 212 : 28; 7) ![]() æ99;
æ99;
2) (32)3; 4) 0,512æ212; 6) (34)5 : 319; 8) 2,55æ405.
234.° Подайте вираз у вигляді степеня та обчисліть його значення (у разі потреби скористайтеся таблицею степенів чисел 2 і 3, розміщеною на форзаці підручника):
9
1) 22æ23; 3) 32æ3æ33; 5) 7 9æ ![]() ;
;
2) (22)3; 4) 0,38 : 0,35; 6) 12,53æ83.
235.° Знайдіть помилки у наведених прикладах:
1) a4a3 = a12; 4) 32æ52 =154; 7) 3æ43 =123;
2) aæa =2a; 5) 22æ7 3 =145; 8) a7b7 = (ab)14;
3) (a3)2 = a9; 6) (2a)4 = 8a4; 9) a3b2 = (ab)6.
236.° Замість зірочки запишіть такий вираз, щоб виконувалася рівність:
1) (*)4 = c20; 2) (*)2 = c14; 3) (*)n = c8n; 4) (*)7 = c7n, де n — натуральне число.
237.• Подайте степінь a7 у вигляді добутку двох степенів з основою a всіма можливими способами.
238.• Подайте у вигляді степеня вираз:
1) ana5; 2) aan; 3) a3an; 4) (a3)n; 5) (an)2æ(a5)n, де n — натуральне число.
239.• Подайте у вигляді степеня вираз:
1) 24æ24; 2) 24 + 24; 3) 2næ2n; 4) 2n + 2n, де n — натуральне число.
240.• Подайте у вигляді степеня вираз:
1) 35 + 35 + 35; 2) 4k + 4k + 4k + 4k, де k — натуральне число.
241.• Доведіть, що коли сторону квадрата збільшити в n разів, то його площа збільшиться в n2 разів.
242.• У скільки разів збільшиться об’єм куба, якщо його ребро збільшити в m разів?
243.• Запишіть у вигляді степеня з показником 2 вираз:
1) a2b6; 2) x8y14; 3) x4y10z18; 4) 4m12n16; 5) 81c10d32p44. 244.• Запишіть у вигляді степеня з показником 3 вираз:
1) a3b6; 2) x9y15; 3) 8x12y18z24; 4) 0,001m30n45.
245.• Подайте у вигляді степеня з основою 5 вираз:
1) 1256; 2) (254)2.
246.• Подайте у вигляді степеня з основою –5 вираз:
1) 6255; 2) ((–25)2)3.
247.• Подайте у вигляді степеня з основою 2 вираз:
1) 8 9æ45; 2) 32æ166æ643.
248.• Знайдіть значення виразу:
4)4 : (65)3; 3) 7(7143æ)6(7æ27)23 ; 5) 328 æ177 8 ; 1) (6
253 æ1252
2) ![]()
![]() 83 : 44; 4) 510 ; 6) 529 æ046 6 .
83 : 44; 4) 510 ; 6) 529 æ046 6 .
|
1) 1005 : 10002; |
43 æ162 3) |
|
310 æ(33)5 2) (3 |
212 4510 . 4) 5 æ |
249.• Обчисліть:
250.• Обчисліть значення виразу:
![]()
![]()
![]()
![]() 91058
91058
1) 1æ; 2) 514æ0,212; 3) 1æ.
251.• Знайдіть значення виразу:
![]() 15
15
1) 105æ0,17; 2) 1,914æ.
252.• Порівняйте значення виразів:
1) (−5)21æ(−5) і (–5)24; 3) (−8)5æ(−8)4 і (–8)8;
2) (−7)8æ(−7)7 і (–7)17; 4) (−6)3æ(−6)9 і (–6)13.
253.• Замініть зірочку таким степенем, щоб виконувалася рівність: 1) 8æ* =28;
2) anæ* a 3n 2, де n — натуральне число.
254.• Запишіть вираз 324 у вигляді степеня з основою:
1) 33; 2) 312; 3) 9; 4) 81.
255.• Запишіть вираз 248 у вигляді степеня з основою:
1) 24; 2) 216; 3) 8; 4) 64.
256.• Розв’яжіть рівняння:
1) x7 = 614; 2) x4 = 512.
257.•• Порівняйте значення виразів:
1) 2300 і 3200; 3) 2720 і 1130; 2) 418 і 189; 4) 310æ58 і 159.
258.•• Порівняйте значення виразів:
1) 1040 і 10 00110; 3) 812 і 596; 2) 1244 і 512; 4) 614 і 216æ312.
259.* Відомо, що сума 625 + 625 + ... + 625 дорівнює 5101. Скільки доданків у цій сумі?
260.* Якою цифрою закінчується значення виразу (n — натуральне число):
1) 4100; 2) 34n; 3) 4n; 4) 3n?
261.* Якою цифрою закінчується значення виразу (n — натуральне число):
1) 92n; 2) 74n; 3) 72n?
262.* Доведіть, що значення виразу:
1) 178 + 19 ділиться націло на 10;
2) 6464 – 1 ділиться націло на 5;
3) 34n + 14, де n — натуральне число, ділиться націло на 5.
263.* Доведіть, що значення виразу:
1) 440 – 1; 2) 2004171 + 1712004 ділиться націло на 5.
264.* Доведіть, що 4825 < 34417.
![]()
265. Сім’я Петренків складається з п’яти осіб: батька, матері, двох дітей шкільного віку та бабусі-пенсіонерки. Щомісячний бюджет сім’ї формується із заробітної плати батька в розмірі 12 300 грн, заробітної плати матері (13 100 грн) та пенсії бабусі (6150 грн). Скільки гривень у місяць припадає на кожного з п’яти членів сім’ї?
266. (Задача з українського фольклору.) Кум Іван спитав у кума Степана: «Скільки в тебе качок?» Кум Степан відповів: «Качок у мене стільки, що як висидять вони мені ще стільки ж каченят, та ще придбаю одну качку, та ще тричі куплю стільки ж, скільки цих качок і каченят, то всього буде їх у мене 100». Скільки качок було в кума Степана?
267. Один маляр може пофарбувати кімнату за 6 год, а другий — за 4 год. Спочатку перший маляр працював 2 год, а потім до нього приєднався другий маляр. За скільки годин було пофарбовано кімнату?
268. Від пристані за течією річки відправилася на човні група туристів і туристок, розраховуючи повернутися через 4 год. Швидкість човна в стоячій воді становить 10 км/год, а швидкість течії — 2 км/год. На яку найбільшу відстань туристи й туристки можуть відплисти від пристані, якщо вони хочуть перед тим, як повертатися, зробити зупинку на 2 год?
269. Розв’яжіть рівняння:
1) 2,5 – 3x = 3 (x – 2,5) – 2;
2) 17 (2 – 3x) – 5 (x + 12) = 8 (1 – 7x) – 34.
270. У шестицифровому числі перша й четверта, друга й п’ята, третя й шоста цифри однакові. Доведіть, що це число кратне числам 7, 11 і 13.
![]() ГОТУЄМОСЯ ДО ВИВЧЕННЯ НОВОЇ ТЕМИ
ГОТУЄМОСЯ ДО ВИВЧЕННЯ НОВОЇ ТЕМИ
271. Спростіть вираз:
1) 3aæ(−1,2); 3) −7aæ9b; 5) −![]() mæ
mæ![]() n;
n;
2) −0,2bæ(−0,5); 4) 2,4xæ2y; 6) −![]() aæ
aæ![]() bæ(−3c).
bæ(−3c).
272. Спростіть вираз 20mæ(−0,3n) і знайдіть його значення при m = ![]() , n = –4.
, n = –4.
 УЧИМОСЯ РОБИТИ НЕСТАНДАРТНІ КРОКИ
УЧИМОСЯ РОБИТИ НЕСТАНДАРТНІ КРОКИ
273. Трамвайні квитки мають номери від 000 000 до 999 999. Номер називають «щасливим», якщо сума трьох його перших цифр дорівнює сумі трьох останніх. Доведіть, що кількість «щасливих» квитків є парною.

Розглянемо вирази:
2b; ![]() xy 2; –ab; m 3æ3k 5; (3,14)2 pq3æ(−7) r 2t 4.
xy 2; –ab; m 3æ3k 5; (3,14)2 pq3æ(−7) r 2t 4.
Кожен із них є добутком чисел, змінних та їхніх степенів. Такі вирази називають одночленами.
Домовилися також вважати одночленами всі числа, будь-які змінні та їхні степені. Так, одночленами є вирази:
–5; 0,3; x; t2; 23.
Зауважимо, що, наприклад, вирази
2a + b, x – 1, a : b, y2 + y – 2
не є одночленами, оскільки вони, крім множення та піднесення до степеня, містять ще й інші дії.
Коли ми бачимо одночлен 3ab3æ ![]() abc, виникає природне бажання спростити його. Маємо:
abc, виникає природне бажання спростити його. Маємо:
3ab3æ ![]() abc 3æ
abc 3æ ![]() aab3bc 2a 2b4c.
aab3bc 2a 2b4c.
Отриманий одночлен містить тільки один числовий множник, відмінний від нуля, який стоїть на першому місці. Усі інші множники — це степені з різними основами. Такий вигляд одночлена називають стандартним виглядом одночлена.
Наведемо ще приклади одночленів стандартного вигляду:
−![]() xy; 2,8a3; 7x2yz3t5.
xy; 2,8a3; 7x2yz3t5.
Зауважимо, що, наприклад, вирази a2æ2b3 і –3x2xy3 не є одночленами стандартного вигляду. Справді, хоча перший із них і має єдиний числовий множник, але він не стоїть на першому місці.
У другому — степінь з основою x записано двічі.
Проте ці одночлени легко привести (перетворити) до стандартного вигляду:
a 2æ2b3 =2a2b3 і –3x2xy3 = –3x3y3.
До одночленів стандартного вигляду також відносять числа, відмінні від нуля, змінні та їхні степені. Так, –2, 32, x, b3 — одночлени стандартного вигляду.
Число 0, а також одночлени, які тотожно дорівнюють нулю, наприклад 0x2, 0ab тощо, називають нуль-одночленами. Їх не відносять до одночленів стандартного вигляду.
Означення. Числовий множник одночлена, записаного в стандартному вигляді, називають коефіцієнтом одночлена.
Наприклад, коефіцієнти одночленів –3a2bc і 0,07x відповідно дорівнюють –3 і 0,07.
Узагалі, будь-який одночлен стандартного вигляду має коефіцієнт. І навіть, наприклад, в одночленів x2y і –mn, у записі яких числовий множник не використовують, коефіцієнтами є числа 1 і –1 відповідно. І це зрозуміло, адже x 2y =1æx 2y, mn 1æmn.
Розглянемо одночлени ![]() x 3yz і –2zx3y. У них однакові буквені частини, тобто буквені частини є тотожно рівними виразами. Такі одночлени називають подібними. До подібних одночленів також відносять і числа. Наприклад, 7 і –5 — подібні одночлени.
x 3yz і –2zx3y. У них однакові буквені частини, тобто буквені частини є тотожно рівними виразами. Такі одночлени називають подібними. До подібних одночленів також відносять і числа. Наприклад, 7 і –5 — подібні одночлени.
Звернемо увагу на те, що, наприклад, в одночленів ![]() x 3y 2z і –2zx3y буквені частини не однакові, хоча й складаються з одних і тих самих змінних. Тому вони не є подібними.
x 3y 2z і –2zx3y буквені частини не однакові, хоча й складаються з одних і тих самих змінних. Тому вони не є подібними.
Означення. Степенем одночлена називають суму показників степенів усіх змінних, що входять до нього. Степінь одночлена, який є числом, відмінним від нуля, вважають рівним нулю.
Також вважають, що нуль-одночлен степеня не має.
Наприклад, степінь одночлена –3,8m2xy7 дорівнює 10, а степені одночленів x3 і 9 дорівнюють відповідно 3 і 0.
Розглянемо два одночлени ![]() ab3 і 10abx. Одночлен
ab3 і 10abx. Одночлен ![]() ab3æ10abx є їхнім добутком. Спростимо його:
ab3æ10abx є їхнім добутком. Спростимо його:
![]() ab3æ10abx
ab3æ10abx ![]() æ10 (aa) (b3b)x 2a 2b4x.
æ10 (aa) (b3b)x 2a 2b4x.
Отже, добутком двох одночленів є одночлен. Його зазвичай записують у стандартному вигляді.
При піднесенні одночлена до степеня також отримують одночлен. Піднесемо, наприклад, до четвертого степеня одночлен 1 xy 3z 2. Маємо:
−
2
44
![]() xy 3z 2
xy 3z 2 ![]() æx 4æ(y 3)4æ(z 2)4
æx 4æ(y 3)4æ(z 2)4 ![]() x 4y 12z 8.
x 4y 12z 8.
![]() ПРИКЛАД 1 Спростіть вираз 0,2a 2b4æ(−5a 3b)2.
ПРИКЛАД 1 Спростіть вираз 0,2a 2b4æ(−5a 3b)2.
Розв’язання. Маємо:
0,2a2b4æ( 5a3b)2 0,2a 2b4æ( 5)2æ(a 3)2b2 0,2a 2b4æ25a6b2
![]() = 0,2æ25a 2a 6b4b2 =5a 8b6. ¤
= 0,2æ25a 2a 6b4b2 =5a 8b6. ¤
![]() ПРИКЛАД 2 Значення змінних a і b такі, що 4a3b4 = 7. Знайдіть
ПРИКЛАД 2 Значення змінних a і b такі, що 4a3b4 = 7. Знайдіть
2 a 6b8. значення виразу −
7
Розв’язання. Маємо:
![]()
![]() a 6b8
a 6b8 ![]() æ16a6b8
æ16a6b8 ![]() æ(4a3b4)2
æ(4a3b4)2 ![]() æ7 2
æ7 2 ![]() æ49
æ49 ![]() . ¤
. ¤
1. Які вирази називають одночленами?
2. ![]() Поясніть, який вигляд одночлена називають його стандартним виглядом.
Поясніть, який вигляд одночлена називають його стандартним виглядом.
3. Що називають коефіцієнтом одночлена?
4. Які одночлени називають подібними?
5. Що називають степенем одночлена?
![]()
274.° Чи є одночленом вираз:
|
1) 5xy; |
4) 8; |
6m k 7) 5 ; 11a |
10) 3 (a2 – b2); |
|
1 2) − a 2b3c; 3 |
5) 0; |
8) b9; |
11) −2 4 aa2b3b6; 9 |
2 3
2
3) m + n; 6) ![]() pk 4; 9) m4m; 12) 1
pk 4; 9) m4m; 12) 1![]() x 5x 3yz10 ?
x 5x 3yz10 ?
275.° Укажіть, які з одночленів записано в стандартному вигляді:
1) 5mnm2; 3) −7t 3æ4t 5; 5) ![]() x 8y 9;
x 8y 9;
|
2) 1,4ab7c3; 4) –abc; 276.° Чи є подібними одночлени: |
6) m 6n 4æ10. |
1) 5a і 7a; 3) 8x2y4 і 8x2y5; 5) ![]() m 7n 8 і
m 7n 8 і ![]() m 8n 7;
m 8n 7;
2) 3a2b3c і 6a2b3c; 4) 3y2 і 2y3; 6) –0,1a9b10 і 0,1a9b10?
277.° Запишіть одночлен, подібний даному, коефіцієнт якого в 4 рази більший за коефіцієнт даного одночлена:
1) 1,4x3y7; 2) c4d10p2; 3) 1![]() a5b5c9.
a5b5c9.
278.° Заповніть таблицю:
|
Одночлен |
Стандартний вигляд одночлена |
Коефіцієнт одночлена |
Степінь одночлена |
|
1,2c4c8 |
|
|
|
|
0 6, m n2 3 æ4m n5 2 |
|
|
|
|
|
|
|
|
|
−5x 2 æ0 2, xy |
|
|
|
|
−1 6, x y3 6 æ0 5, x y2 5 |
|
|
|
279.° Зведіть одночлен до стандартного вигляду, укажіть його коефіцієнт і степінь:
|
1) 9a4aa6; |
3) 7aæ(−9ac); |
5) −5x 2æ0,1x 2yæ(−2y); |
|
2) 3xæ0,4yæ6z; |
4) −3 1 m 5æ9mn 9; |
6) cæ(−d)æc18. |
3
280.° Подайте одночлен у стандартному вигляді, підкресліть його коефіцієнт:
1) 6bb2; 3) −0,8u 4æ4t 3æ(−2t7 );
2) 1,5c3d 4æ8c2d 5; 4) 4,5a 2bc7 æ1![]() a 8b6c.
a 8b6c.
281.° Знайдіть значення одночлена:
1) 5x2, якщо x 4;
2) −4,8a 4b3, якщо a 1, b = ![]() ;
;
3) 0,04c3d 5, якщо c 10, d = 2; 4) ![]() m 3n 2 p3, якщо m 3, n =5, p 1.
m 3n 2 p3, якщо m 3, n =5, p 1.
282.° Знайдіть значення одночлена:
1) 3m 3, якщо m 3;
2) ![]() a 2b4, якщо a
a 2b4, якщо a ![]() , b =2;
, b =2;
3) 0,8m 2n 2k, якщо m = 0,3, n = ![]() , k =2000.
, k =2000.
283.° Знайдіть добуток одночленів:
1) 2a і 5b; 3) 6x і –8y2;
2) –m і 4n; 4) −1 x 3 і –7x2.
7 284.° Виконайте множення одночленів:
1) 0,6a 4b3æ4a 2b; 4) 0,7x 6y 9æ0,3xy;
2) ![]() −2,8x 2y 5æ0,5x 4y 6; 5) − 3 p2q8æp8q2;
−2,8x 2y 5æ0,5x 4y 6; 5) − 3 p2q8æp8q2;
20
3) 13c2dæ(−3cd); 6) −6 ![]() mn 8 p11æ3
mn 8 p11æ3![]() m 5n 5.
m 5n 5.
285.° Спростіть вираз:
1) 12a 2æ5a 3b7; 4) 56x 5y 14æ![]() x 2y;
x 2y;
|
2) −4m 3æ0,25m 6; |
1 5) − p2æ(−27k)æ5pk; 3 |
3) 3abæ(−17a2b); 6) 2![]() b2c5d 3æ 3
b2c5d 3æ 3![]() b3c4d 7 .
b3c4d 7 .
286.° Піднесіть до квадрата одночлен:
|
1) 6a; |
4) –0,2m8n9; |
|
2) 3b2; |
1 5) x y3 6; 8 |
|
3) –9a4b5; |
5 6) − ab c2 8. |
7
287.° Піднесіть до куба одночлен:
1) 2b; 3) 1 x 5; 5) −1 x y3 2;
3 4
2) 10c4; 4) –0,1m7n10; 6) –a3b2c.
288.° Перетворіть в одночлен стандартного вигляду вираз:
4
1) (3a2b)2; 3) (−10m 2y 8)5; 5) ![]() c6d ;
c6d ;
6
2) (−0,2x 3y 4)3; 4) (16x 6y 7z 8)2; 6) 1![]() a 8b9 .
a 8b9 .
289.° Виконайте піднесення до степеня:
5
1) (−6m 3n 3)3; 3) (0,5a12b14)2; 5) ![]() x 8y 9 ;
x 8y 9 ;
2
2) (−7x 9y 10)2; 4) (3ab4c5)4; 6) 2![]() a 6b8 .
a 6b8 .
290.° Чи є правильним твердження (відповідь обґрунтуйте):
1) одночлен 6x2 при будь-яких значеннях x набуває додатних значень;
2) одночлен 0,4a4b6 при будь-яких значеннях a і b набуває невід’ємних значень;
1 a 3 при будь-яких значеннях a набуває від’ємних
3) одночлен −
3
значень;
4) одночлен –5b2 при будь-яких значеннях b набуває від’ємних значень?
291.• Подайте даний вираз у вигляді добутку двох одночленів, один з яких дорівнює 3a 2b6 :
1) 3a 6b8; 2) −12a 2b10; 3) −2,7a5b7; 4) 2![]() a 20b30.
a 20b30.
292.• Яким одночленом треба замінити зірочку, щоб виконувалася рівність:
1) *æ3b4 =12b6; 3) 7a 3b9æ* 4,2a5b12;
2) 5a5b2æ* 20a 6b8; 4) 23a12b16æ* 23a 29b17 ?
293.• Виконайте множення одночленів, де m і n — натуральні числа:
1) 2![]() an 2bm 3æ
an 2bm 3æ![]() a5n 4b2m 1; 2) 7
a5n 4b2m 1; 2) 7 ![]() a 2n 1b3n 1æ1
a 2n 1b3n 1æ1![]() an 6b3n 1.
an 6b3n 1.
294.• Подайте у вигляді квадрата одночлена стандартного вигляду вираз:
|
1) 4a10; |
3) 0,16a14b16; |
|
2) 36a 8b2; |
4) 289a 20b30c40. |
295.• Подайте у вигляді куба одночлена стандартного вигляду вираз:
1) 8x 6; 3) 0,001x 12y 18;
2) −27x 3y 9; 4) −125 x 15y 21z 24.
216
296.• Подайте одночлен 64a 6b12 у вигляді:
1) добутку двох одночленів, один з яких дорівнює 2a 2b8;
2) квадрата одночлена стандартного вигляду;3) куба одночлена стандартного вигляду.
297.• Подайте одночлен 81m 4n 16 у вигляді:
1) добутку двох одночленів, один з яких дорівнює −![]() mn 14;
mn 14;
2) квадрата одночлена стандартного вигляду;
3) четвертого степеня одночлена стандартного вигляду.298.• Спростіть вираз:
2
1) 2a 3æ(−5a 4b5)2; 4) 1![]() m 4n 9æ
m 4n 9æ ![]() mn 3 ;
mn 3 ;
4
2) (−x 6y)3æ11x 4y 5; 5) 1![]() x 7y 2æ
x 7y 2æ ![]() x 2y 9 ;
x 2y 9 ;
4
3) (−0,6a 3b5c6)2æ3a 2c8; 6) ( 2c2d 5)7 æ ![]() c4d 5 .
c4d 5 .
|
299.• Спростіть вираз: |
|
|
1) 20a 8æ(9a)2; |
4) (0,2x 7y 8)3æ6x 2y 2; |
3
2) (−b5)4æ12b6; 5) ![]() ab4 æ(4a 6)2;
ab4 æ(4a 6)2;
52
3) (3m 6n 3)4æ ![]() m 9n ; 6)
m 9n ; 6) ![]() x 2y æ
x 2y æ ![]() xy 2 .
xy 2 .
300.•• Замініть зірочки такими одночленами, щоб виконувалася рівність:
1) (*)2æ(*)3 = 9a 2b3c5; 3) (*)3æ(*)2 72m 8n 11;
2) (*)3æ(*)4 =16a7b6c8; 4) (*)2æ(*)5 =32x 29y 21z 9.
301.•• Значення змінних x і y такі, що 5x 2y 4 = 6. Знайдіть значення
виразу:
1) 1,5x 2y 4; 2) 25x 4y 8; 3) –25x6y12.
302.•• Значення змінних a і b такі, що 3ab3 = 4. Знайдіть значення виразу:
1) −1,2ab3; 2) 27a 3b9; 3) −2 a2b6.
3
303.•• Значення змінних a, b і c такі, що 2a 2b =7, a3c2 = 2. Знайдіть значення виразу:
1) 6a5bc2; 2) a7b2c2; 3) 2![]() a 8bc4.
a 8bc4.
304.•• Значення змінних m, n і p такі, що m 3n 2 =3, 1 n 3 p2 =5. Знай-
3
|
діть значення виразу: |
|
|
1) m 3n 5 p2; 2) 2m3n8p4; |
3) −0,4m12n 11 p2. |
![]()
305. У магазині канцтоварів продавець сказав Дмитру, що за 9 однакових наборів фломастерів треба заплатити 245 грн. Дмитро одразу ж сказав, що продавець помилився. Як він це визначив?
306. Сорочка спочатку подешевшала на 10 %, а потім подорожчала на 20 %. У результаті цих двох переоцінок виявилося, що ціна сорочки змінилася на 48 грн. Знайдіть початкову ціну сорочки.
307. (Задача з російського фольклору.) Летіла зграя гусей, а назустріч їм летить одна гуска й каже: «Здрастуйте, сто гусей!» — «Нас не сто гусей, — відповідає їй вожак зграї, — якби нас було стільки, скільки зараз, та ще стільки, та півстільки, та чверть стільки, та ще ти, гуско, то тоді нас було б сто гусей». Скільки гусей було в зграї?
308. Замініть зірочки такими цифрами, щоб: 1) число *5* ділилося націло на 3 і на 10;
2) число 13*2* ділилося націло на 9 і на 5; 3) число 58* ділилося націло на 2 і на 3. Знайдіть усі можливі розв’язки.
![]() ГОТУЄМОСЯ ДО ВИВЧЕННЯ НОВОЇ ТЕМИ
ГОТУЄМОСЯ ДО ВИВЧЕННЯ НОВОЇ ТЕМИ
309. Спростіть вираз:
1) 6x 12x 15x 9x ; 3) 0,8k 0,9 1,7k 0,5k 1,4;
2) 7a 9b 12a 14b; 4) ![]() a
a ![]() b
b ![]() a
a ![]() b.
b.
 УЧИМОСЯ РОБИТИ НЕСТАНДАРТНІ КРОКИ
УЧИМОСЯ РОБИТИ НЕСТАНДАРТНІ КРОКИ
310. Скількома способами можна поставити на шахову дошку білу й чорну тури так, щоб вони не били одна одну?

У попередньому пункті ви дізналися, що добуток одночленів є одночленом. Інша справа із сумою одночленів. Наприклад, вирази 2a +b2 і 2a −b2 не є одночленами. Перший із них є сумою одночленів 2a і b2, а другий — сумою одночленів 2a і −b2.
Означення. Вираз, який є сумою кількох одночленів, називають многочленом.
Ось ще приклади многочленів: 7xy y 11; x 4 2x 3 5x 2 x 1; 3a a b; 11x −2x .
Одночлени, з яких складено многочлен, називають членами многочлена. Так, членами многочлена 7xy y 11 є одночлени 7xy, y і –11.
Многочлен, який складається з двох членів, називають двочленом, а той, який складається з трьох членів, — тричленом. Домовилися розглядати одночлен як окремий вид многочлена.
Вважають, що такий многочлен складається з одного члена.
Зв’язки між многочленами, одночленами та їхнім окремим видом — числами ілюструє схема, зображена на рисунку 5.

Рис. 5
Якщо серед одночленів, з яких складається многочлен, є подібні, то їх називають подібними членами многочлена. Наприклад, у многочлені 7a b2 − 3a + −4 a b2 − + +1 a b подібні члени підкрес-
![]()
лено однаковою кількістю рисочок.
Використовуючи правило зведення подібних доданків, спростимо цей многочлен:
7a 2b 3a 4 a 2b 1 a b 6a 2b 2a b 3.
Таке спрощення називають зведенням подібних членів многочлена. Це перетворення дає змогу замінити многочлен на тотожно рівний йому, але простіший — з меншою кількістю членів.
Розглянемо многочлен 2x 3y xy 1. Цей многочлен складений з одночленів стандартного вигляду, серед яких немає подібних.
Означення. Многочлен, складений з одночленів стандартного вигляду, серед яких немає подібних, називають многочленом стандартного вигляду.
Многочлени xy 2 + x 2y, 2a2b, 5 є прикладами многочленів стандартного вигляду.
Зауважимо, що многочлен 3bab2 aæ5 aæ2b3 a не є многочленом стандартного вигляду. Проте його можна перетворити в многочлен стандартного вигляду таким чином: записати в стандартному вигляді одночлени, з яких він складений, а потім звести подібні доданки.
Маємо: 3bab2 aæ5 aæ2b3 a 3ab3 5a 2ab3 a 5ab3 4a.
![]()
Розглянемо многочлен стандартного вигляду 2х3y – х2y2 + 5х2y + + y – 2. Він складений з одночленів: 2x 3y; −x 2y 2; 5x 2y; y; –2, степені яких відповідно дорівнюють числам 4, 4, 3, 1, 0. Найбільший із цих степенів дорівнює числу 4. У цьому разі говорять, що степінь многочлена 2x 3y x 2y 2 5x 2y y 2 дорівнює 4.
Означення. Степенем многочлена стандартного вигляду називають найбільший зі степенів одночленів, з яких цей многочлен складений.
Наведемо ще приклади:
• степінь многочлена 3x 2 xy 5y 2 дорівнює двом;
• степінь многочлена 3x 4y 2 дорівнює шести;
• степінь многочлена 3 дорівнює нулю.
Число 0, а також многочлени, які тотожно дорівнюють нулю (наприклад, 0a + 0b, x – x і т. п.), називають нуль-многочленами.
Їх не відносять до многочленів стандартного вигляду.
Вважають, що нуль-многочлен степеня не має.
1. Що називають многочленом?
2. Який многочлен називають двочленом? тричленом?
3. Що називають подібними членами многочлена?
4. ![]() Який многочлен називають многочленом стандартного вигляду?
Який многочлен називають многочленом стандартного вигляду?
5. Що називають степенем многочлена стандартного вигляду?
ВПРАВИ
311.° Чи є многочленом вираз:
1) x2 + 1; 3) ![]() x 21+1; 5) xy (x3 – 3y); 7) (m + 1) (m – 4);
x 21+1; 5) xy (x3 – 3y); 7) (m + 1) (m – 4);
2) 4x y2 æ3y; 4) 9; 6) 2x3 – 2x + 2; 8) (x + 3y)2?
312.° Назвіть одночлени, сумою яких є даний многочлен:
1) 5a 4 3a 2 a 8; 3) t 3 3t 2 4t 5;
2) 6x 3 10x 2y 7xy 2 y 3; 4) 1,8a 3b 3,7a 2b2 16ab3 b4.
313.° Запишіть многочлен, який складається з одночленів:
1) 3a і 2b; 3) x3, 2x2 і –3x; 2) 6c і –5p; 4) x2, –xy і y2.
314.° Запишіть многочлен, який складається з одночленів:
1) –4a і 5b; 3) a2, 2ab і b2; 2) p2 і –5p; 4) x4, –x3y, x2y2 і –xy3.
315.° Знайдіть значення многочлена: 1) 2x 2 x 3 при x = 0,5;
2) x 3 +5xy при x =3, y 2;
3) a2 2ab b2 при a 4, b =6;
4) y 4 7y 3 2y 2 y 10 при y 1.
316.° Знайдіть значення многочлена 2y 3 3y 2 4y 6 при:
1) y =1; 2) y = 0; 3) y 5.
317.° Чи є даний многочлен многочленом третього степеня: 1) 3a2 + 3a + 3; 3) a2 + 2a – 6; 5) a3 + a2b2 + b3; 2) a3 – 1; 4) a2b + b2 – 1; 6) a3 + a + 1?
318.° Чи є даний многочлен многочленом четвертого степеня:
1) a4 + 2a2 – 1; 3) a4 + a2b2 – a4;
2) aa3 – 5a + 6; 4) a3b – 2ab3 + b5?
319.° Перетворіть многочлен у многочлен стандартного вигляду.
Укажіть його степінь:
1) 4b2 a2 9ab 18b2 9ab;
2) 8m 3 −13mn −9n 2 −8m 3 −2mn;
3) 2a 2b 7ab2 3a 2b 2ab2;
4) 0,9c4 1,1c2 c4 0,6c2;
5) 3x 2 6x 5 x 2 10x 3; 6) b3 3bc 3b3 8bc 4b3.
320.° Перетворіть многочлен у многочлен стандартного вигляду.
Укажіть його степінь:
1) 5x 2 10x 9 2x 2 14x 20;
2) m 5 2m 4 6m 5 12m 3 18m 3;
3) 0,2a 3 1,4a 2 2,2 0,9a 3 1,8a 2 3; 4) 6x 2y xy 2 8x 2y 2xy 2 xy 7.
321.° Закінчіть розташування членів многочлена в порядку спадання степенів змінної:
1) 8x – 3x2 + 6x3 – 4 = 6x3 – 3x2 + ...;
2) x4 – 5x6 – 3x2 + 3x3 – 7x + 2 = –5x6 + x4 + ...; 3) 3 – 10x5 + x = –10x5 + ... .
322.° Розташуйте члени многочлена в порядку зростання степенів змінної:
1) 4m3 – 5m – m2 + 6;
2) 9a – 8a4 + 5a3 + 7 – a2; 3) 8m4 – 4 + 7m6 – 10m3 + m2.
323.• Зведіть подібні члени та знайдіть значення многочлена при вказаних значеннях змінних:
1) 3a 5 4a 3 7a 5 10a 3 12a, якщо a 2;
2) x3y – 3xy2 – 4x3y + 8xy2, якщо x 1, y 3; 3) 0,8x 2 0,3x x 2 1,6 1,1x 0,6, якщо x =5;
4) 1 a 2c + 3 ac2 + 1 a2c +1,25ac2, якщо a 4, c = 3.
3 4 6
324.• Зведіть подібні члени та знайдіть значення многочлена при вказаних значеннях змінних:
1) 2a 3 3ab b2 6a 3 7ab 2b2, якщо a =2, b = –6; 2) mn −6mn 2 −8mn −6mn 2, якщо m = 0,5, n = –2; 3) 10xy 2 12x 2y 9x 2y 9xy 2, якщо x = ![]() , y = 9. 325.• З одночленів 4a, −3ab, 7a 2, −8a 2, 9ab, 5a виберіть кілька та складіть із них:
, y = 9. 325.• З одночленів 4a, −3ab, 7a 2, −8a 2, 9ab, 5a виберіть кілька та складіть із них:
1) многочлен стандартного вигляду;
2) многочлен, який містить подібні члени;
3) два многочлени стандартного вигляду, використавши при цьому всі дані одночлени.
![]()
326. На рулоні шпалер написано, що довжина полотна шпалер відрізняється від номінальної не більше ніж на 0,8 %. Номінальна довжина полотна в рулоні дорівнює 10 м. Укажіть, якій з наведених величин не може дорівнювати довжина шпалер у цьому рулоні.
1) 10,06 м; 2) 9,94 м; 3) 9,9 м; 4) 10,02 м.
327. Цукерки за ціною 42 грн за 1 кг змішали із цукерками за ціною 57 грн за 1 кг і отримали суміш за ціною 48 грн за 1 кг. Яка маса цукерок кожного виду міститься в 1 кг суміші?
328. За зняття готівкових грошей у банкоматі деякого банку стягується комісія в розмірі 1,5 % від суми, що знімається. Яку суму буде списано з банківського рахунка під час зняття в банкоматі 2000 грн готівкою?
329. Крамниця закупає чашки за оптовою ціною 120 грн за одну штуку та продає з націнкою 30 %. Скільки коштуватиме така чашка в цій крамниці?
![]() ГОТУЄМОСЯ ДО ВИВЧЕННЯ НОВОЇ ТЕМИ
ГОТУЄМОСЯ ДО ВИВЧЕННЯ НОВОЇ ТЕМИ
330. Якому з поданих виразів тотожно дорівнює вираз 9x (4x 7):
1) 13x −7; 3) −5x −7;
2) 5x 7; 4) 13x +7?
331. Якому з поданих виразів тотожно дорівнює вираз −8y −(3y −1):
1) 11y 1; 3) −11y −1; 2) 5y 1; 4) −5y −1?
332. Спростіть вираз:
1) (2a b) (b 2a); 3) (m n) (2m n) (m 4n); 2) (3a 4) (3 5a); 4) (5c 2) (6c 1) (c 8).
Поновіть у пам’яті зміст п. 24 на с. 272.
 УЧИМОСЯ РОБИТИ НЕСТАНДАРТНІ КРОКИ
УЧИМОСЯ РОБИТИ НЕСТАНДАРТНІ КРОКИ
333. Навколо зорі обертається кілька планет, відстані між якими не змінюються та є попарно різними. На кожній планеті перебуває один астроном, який спостерігає за найближчою планетою. Доведіть, що існують дві планети, на яких астрономи спостерігають один за одним.
![]() 9. Додавання і віднімання многочленів
9. Додавання і віднімання многочленів
Нехай треба додати два многочлени 3xy 2 5x 2y 2 7xy x 11 і 2xy 2 x 2y 2 2xy y 2. Для цього візьмемо їх у дужки й поставимо між ними знак «плюс». Потім розкриємо дужки та зведемо подібні доданки (якщо такі є).
Отримуємо:
(3xy 2 5x 2y 2 7xy x 11) ( 2xy 2 x 2y 2 2xy y 2)
3xy 2 5x 2y 2 7xy x 11 2xy 2 x 2y 2 2xy y 2
![]()
xy 2 6x 2y 2 5xy x y 9.
Отриманий многочлен є сумою двох даних многочленів.
Нехай тепер треба від першого многочлена відняти другий. Для цього кожний із многочленів візьмемо в дужки й поставимо перед від’ємником знак «мінус». Потім розкриємо дужки та зведемо подібні доданки.
Маємо:
(3xy 2 5x 2y 2 7xy x 11) ( 2xy 2 x 2y 2 2xy y 2)
= 3xy 2 5x 2y 2 7xy x 11 2xy 2 x 2y 2 2xy y 2
![]()
5xy 2 4x 2y 2 9xy x y 13.
Отриманий многочлен є різницею двох даних многочленів.
При додаванні та відніманні многочленів завжди отримуємо многочлен.
![]() ПРИКЛАД 1 Доведіть, що різниця двоцифрового числа й числа, записаного тими самими цифрами, але у зворотному порядку, ділиться націло на 9.
ПРИКЛАД 1 Доведіть, що різниця двоцифрового числа й числа, записаного тими самими цифрами, але у зворотному порядку, ділиться націло на 9.
Розв’язання. Нехай дане число має a десятків і b одиниць.
Тоді воно дорівнює 10a + b.
Число, записане тими самими цифрами у зворотному порядку, дорівнює 10b + a.
Розглянемо різницю (10a + b) – (10b + a) = 10a + b – 10b – a = = 9a – 9b = 9 (a – b).
Очевидно, що число 9 (a – b) ділиться націло на 9. ¤
![]()
![]() Запис ab є позначенням двоцифрового числа, яке має a десят-
Запис ab є позначенням двоцифрового числа, яке має a десят-
![]()
![]() ків і b одиниць, тобто ab 10a b. Аналогічно запис abc є позначенням трицифрового числа, яке має a сотень, b десятків і c одиниць, тобто abc 100a 10b c.
ків і b одиниць, тобто ab 10a b. Аналогічно запис abc є позначенням трицифрового числа, яке має a сотень, b десятків і c одиниць, тобто abc 100a 10b c.
![]() ПРИКЛАД 2 Доведіть, що різниця ab ac bc литься націло на 18.
ПРИКЛАД 2 Доведіть, що різниця ab ac bc литься націло на 18.
Розв’язання. Маємо: ab ac bc ba ca cb
(10a b 10a c 10b c) (10b a 10c a 10c b) (20a 11b 2c) (20c 11b 2a) 20a 11b 2c 20c 11b 2a 18a 18c 18 (a c).
![]() Очевидно, що число 18 (a – c) ділиться націло на 18.
Очевидно, що число 18 (a – c) ділиться націло на 18. ¤
![]() ПРИКЛАД 3 Доведіть, що сума чотирьох послідовних парних нату ральних чисел не ділиться націло на 8.
ПРИКЛАД 3 Доведіть, що сума чотирьох послідовних парних нату ральних чисел не ділиться націло на 8.
Розв’язання. Нехай перше із цих чисел дорівнює 2n, де n — довільне натуральне число. Тоді наступними трьома числами є 2n + 2, 2n + 4, 2n + 6 відповідно.
Розглядувана сума має такий вигляд:
2n + (2n + 2) + (2n + 4) + (2n + 6) = 8n + 12.
Перший доданок 8n суми 8n + 12 ділиться націло на 8, а другий доданок 12 — не ділиться. Отже, сума 8n + 12 не ділиться націло  на 8.
на 8. ¤
334.° Знайдіть суму многочленів: 1) –6 – a2 і a2 + 13; 2) a2 – b + c3 і –a2 + b + c2; 3) 3x + 14 і –x2 – 3x – 18.
335.° Знайдіть суму многочленів:
1) –5x2 – 4 і 8x2 – 6; 2) 2x + 16 і –x2 – 6x – 20.
336.° Знайдіть різницю многочленів:
1) x2 + 8x і 4 – 3x; 3) 4x2 – 7x + 3 і x2 – 8x + 11;
2) 2x2 + 5x і 4x2 – 2x; 4) 9m2 – 5m + 4 і –10m + m3 + 5.
337.° Знайдіть різницю многочленів:
1) –5,4m + n2 і n2 + 3,9m; 3) 3x2 – 6x + 2 і x2 – 7x + 15. 2) a2 – b2 і –b2 + a2 – c2;
338.° Знайдіть суму і різницю двочленів:
1) a + b і a – b; 3) b – a і a – b; 2) a – b і b – a; 4) b – a і –a – b.
339.° Знайдіть суму і різницю двочленів: 1) 2a – b і 3a + b; 3) 2a + b і 3a – b; 2) b – 2a і b – 3a; 4) b – 2a і 3a – b.
340.° Спростіть вираз:
1) (5a 4 3a 2b b3) (3a 4 4a 2b b2);
2) (12xy 10x 2 9y 2) ( 14x 2 9xy 14y 2); 3) (7ab2 8ab 4a 2b) (10ab 7a 2b); 4) (2c2 3c) ( c2 c) (c2 4c 1).
341.° Спростіть вираз:
1) (3x 2 2x) ( x 2 3x);
2) (4c2 2cd) (10c2 8cd); 3) (12m 2 7n 3mn) (6mn 10n 14m 2); 4) (3n 3 2mn 4m 3) (2mn 3n 3).
342.° Який двочлен треба додати до даного двочлена, щоб їхня сума тотожно дорівнювала нулю:
1) a + b; 2) a – b; 3) –a – b?
343.° Розв’яжіть рівняння:
1) 10 – (7 – 4x – x2) = x2 + 8x – 9;
2) (5x 2 3) (2x 5) 5x 2;
3) 6 + x3 – (2x – 9 + x3) = 5;
4) 12 (6 9x x 2 ) x 2 5x 14.
344.° Розв’яжіть рівняння:
1) 5y3 – (6y + 1) = 19 – 2y + 5y3; 2) 7x – 2x2 – (10 – 2x2) = 11; 3) 8x2 + 6x – (2x + 8x2 – 12) = 4.
345.• Розв’яжіть рівняння:
1) 3x 2 (2x 2 8x) (x 2 3) x ;
2) 4y 3 (4y 3 8y) (6y 3) 7; 3) (y 2 4y 17) (6y 2 3y 8) 1 y 5y 2.
346.• Розв’яжіть рівняння:
1) x 2 (x 1) (x 2 7x 32) 3;
2) (y 3 3y 8) (5y y 3 7) 2y 3 2y 15.
347.• Доведіть тотожність:
1) (a 2 b2 c2) (b2 c2 a 2) (c2 a2) a 2 c2;
2) (4 3a 2) a 2 (7 2a 2) ( 2a 2 11) 0; 3) (x 3 4x 2) (x 6) (1 x x 3) 4x 2 5.
348.• Доведіть тотожність:
1) 4a 2 (6a 2 2ab) (3ab 2a 2) 5ab; 2) (9x 6 4x 3) (x 3 9) (8x 6 5x 3) x 6 9.
349.• Знайдіть значення виразу:
1) (5a 3 −20a 2) −(4a 3 −18a 2), якщо a 3; 2) 4b2 (7b2 3bc) (3b2 7bc), якщо b 1,5, c = 4.
350.• Обчисліть значення виразу:
1) (5,7a 2 2,1ab b2) (3,9ab 0,3a 2 2b2), якщо a 1, b =5;
2) (5m 2n m 3) 7m 3 (6m 3 3m 2n), якщо m ![]() , n =
, n = ![]() .
.
351.• Доведіть, що значення виразу не залежить від значення змінної, що входить до нього: 1) 1,6 7a 2 (0,8 4a 2) (3a 2 0,7);
2) 3x 2 −9x −(8 −5x 2 −(9x −8x 2)).
352.• Доведіть, що значення виразу (2c2 3c) 1,8 c2 (c2 3c 2,2) не залежить від значення змінної, що входить до нього.
353.• Який многочлен треба додати до тричлена 2a 2 5a 7, щоб їхня сума дорівнювала:
1) 5; 2) 0; 3) a 2; 4) –2a?
354.• Який многочлен треба відняти від двочлена 4a 3 −8, щоб їхня різниця дорівнювала:
1) –4; 2) 9; 3) −2a 3; 4) 3a?
355.• Замість зірочки запишіть такий многочлен, щоб утворилася тотожність:
1) * (3x 2 4xy 2y 2) 9x 2 y 2; 2) a 3 6a 2 2a (*) a 5 2a 2 7.
356.• Замість зірочки запишіть такий многочлен, щоб утворилася тотожність:
1) (2x 2 14x 9) (*) 20 10x ; 2) (19a 4 17a 2b b3) (*) 20a 4 5a2b.
357.• Замість зірочки запишіть такий многочлен, щоби після зведення подібних членів отриманий многочлен не містив змінної a:
1) 4a 2 3ab b 8 *;
2) 9a 3 9a 7ab2 bc bm *.
358.• Замість зірочки запишіть такий многочлен, щоби після зведення подібних членів многочлен 3x 2 5x 2y 7x 8y 15 * не містив:
1) членів з x 2; 2) членів зі змінною x; 3) членів зі змінною y.
359.• Подайте у вигляді многочлена число, яке складається:
1) із 4 сотень, x десятків і y одиниць; 2) з a тисяч, b сотень, 5 десятків і c одиниць.
360.• Подайте у вигляді многочлена вираз:
![]()
1) ![]() cba; 3) a0c + ac.
cba; 3) a0c + ac.
2) abc −ab;
361.• Подайте у вигляді многочлена вираз:
![]()
1) cab+ ca; 3) ab9 +7a.
2) abc +bca;
362.• Доведіть, що значення виразу (9 – 18n) – (6n – 7) кратне 8 при будь-якому натуральному значенні n.
363.• Доведіть, що значення виразу (6m + 8) – (3m – 4) кратне 3 при будь-якому натуральному значенні m.
364.• Доведіть, що при будь-якому натуральному n значення виразу (5n 9) (5 2n) при діленні на 7 дає остачу, яка дорівнює 4.
365.• Чому дорівнює остача при діленні на 9 значення виразу (16n 8) (7n 3), де n — довільне натуральне число?
366.• Подайте многочлен 3a2b 8a 3 6a 12b 9 у вигляді суми двох многочленів таких, щоб один із них не містив змінної b.
367.• Подайте многочлен 4mn 2 11m 4 7m 5 14mn 9n 3 у вигляді різниці двох многочленів з додатними коефіцієнтами.
368.• Подайте многочлен 6x 2 3xy 5x 8y 2 у вигляді різниці двох многочленів таких, щоб один із них не містив змінної y.
369.• Доведіть, що значення різниці двочленів 13m + 20n і 7m + 2n, де m і n — довільні натуральні числа, ділиться націло на 6.
370.• Доведіть, що значення суми двочленів 16a −6b і 27b−2a, де a і b — довільні натуральні числа, ділиться націло на 7.
371.• Подайте многочлен x 2 6x 14 у вигляді різниці:
1) двох двочленів; 2) тричлена й двочлена.
372.• Подайте многочлен 3x 2 10x 5 у вигляді різниці двочлена й тричлена.
373.•• Доведіть, що вираз (2x 4 4x 1) (x 2 8 9x) (5x x 2 3x 4) набуває від’ємного значення при будь-якому значенні x. Якого найбільшого значення набуває цей вираз і при якому значенні x?
374.•• Доведіть, що вираз (7y 2 9y 8) (3y 2 6y 4) 3y набуває додатного значення при будь-якому значенні y. Якого найменшого значення набуває цей вираз і при якому значенні y?
375.•• Доведіть, що:
1) сума п’яти послідовних натуральних чисел ділиться націло на 5;
2) сума трьох послідовних парних натуральних чисел ділиться націло на 6;
3) сума чотирьох послідовних непарних натуральних чисел ділиться націло на 8;
4) сума чотирьох послідовних натуральних чисел не ділиться націло на 4;
5) остача від ділення на 6 суми шести послідовних натуральних чисел дорівнює 3.
376.•• Доведіть, що:
1) сума трьох послідовних натуральних чисел кратна 3;
2) сума семи послідовних натуральних чисел ділиться націло на 7;
3) сума чотирьох послідовних парних натуральних чисел ділиться націло на 4;
4) сума п’яти послідовних парних натуральних чисел ділиться націло на 10.
¿ 377.•• Доведіть, що:
1) ![]() сума чисел ab, bc і ca ділиться націло на 11;
сума чисел ab, bc і ca ділиться націло на 11;
2) різниця чисел abc і cba ділиться націло на 99.
378.•• Доведіть, що:
1) сума чисел abc, bca і cab кратна 111;
2) різниця числа abc і суми його цифр ділиться націло на 9.
379.•• Доведіть, що не існує таких значень x і y, при яких многочлени 5x 2 −6xy −7y 2 і 3x 2 6xy 8y 2 одночасно набували б від’ємних значень.
380.•• Розставте дужки так, щоб рівність стала тотожністю:
1) x 2 2x 1 x 2 2x 1 2;
2) x 2 2x 1 x 2 2x 1 2; 3) x 2 2x 1 x 2 2x 1 0.
![]()
381. На діаграмі (рис. 6) відображено об’єми продажу ручок у крамниці канцтоварів протягом 6 місяців. Скільки ручок продавали в середньому щомісячно?
330
![]()
![]() 300
300
270
240
210
180
150
120
90
Ëèïåíü Ñåðïåíü Âåðåñåíü Æîâòåíü Ëèñòîïàä Ãðóäåíü
Рис. 6
382. У листопаді телевізор коштував 22 000 грн. З 1 грудня магазин підвищив на 15 % ціну телевізора. 15 грудня в магазині оголосили про початок проведення передноворічних святкових продажів і знизили ціни на телевізори на 10 %. Коли було вигідніше купити телевізор: у листопаді чи під час передноворічних розпродажів?
383. Пальто коштувало 4000 грн. Спочатку його ціну знизили на 5 %, а потім підвищили на 5 %. Якою стала нова ціна пальто?
384. Через першу трубу басейн можна наповнити водою за 3 год, а через другу — за 6 год. Спочатку 2 год була відкрита перша труба, потім її закрили, але відкрили другу. За скільки годин було наповнено басейн?
385. Відомо, що в парку ![]() кількості дерев становлять каштани, а
кількості дерев становлять каштани, а ![]() — берези. Скільки всього дерев у парку, якщо їх більше за 100, але менше від 200?
— берези. Скільки всього дерев у парку, якщо їх більше за 100, але менше від 200?
386. Із села до станції вийшов пішохід зі швидкістю 4 км/год. Через годину із села зі швидкістю 10 км/год виїхав велосипедист, який прибув на станцію на 0,5 год раніше за пішохода. Яка відстань від села до станції?
завдання № 2 «Перевірте себе» в тестовій формі
![]()
387. Знайдіть значення виразу, використовуючи розподільну властивість множення:
1) 12æ ![]() ; 2) 36æ
; 2) 36æ ![]() ; 3)
; 3) ![]() æ
æ![]() .
.
|
388. Розкрийте дужки: |
|
|
1) 4 (2a −3b); |
3) ( 2,6m 3,5n 7,2)æ( 10); |
|
2) 0,3 (9x 5y 7); 389. Спростіть вираз: |
4) m ( n 8k 12). |
|
1) 3m 2næ0,4mn 3; |
3) −5x 4y 2z 8æ(−0,8x 6y 8z 2); |
2) 7 ![]() b3c2æ
b3c2æ![]() a 4b5; 4) −5
a 4b5; 4) −5![]() abcæ3,5a12b10c.
abcæ3,5a12b10c.
Поновіть у пам’яті зміст п. 11 на с. 268, 269.
 УЧИМОСЯ РОБИТИ НЕСТАНДАРТНІ КРОКИ
УЧИМОСЯ РОБИТИ НЕСТАНДАРТНІ КРОКИ
390. Сашко й Наталка записують 30-цифрове число, використовуючи тільки цифри 1, 2, 3, 4, 5. Першу цифру пише Сашко, другу — Наталка й т. д. Наталка хоче отримати число, кратне 9. Чи зможе Сашко їй завадити?
ЗАВДАННЯ № 2 «ПЕРЕВІРТЕ СЕБЕ» В ТЕСТОВІЙ ФОРМІ
1. Яка з наведених рівностей не є тотожністю?
А) –3 (a – b) = –3a + 3b; Б) 9a – 8a + a = 2a;
В) 8a – (4a + 1) = 4a – 1;
Г) –(x + 3y) + (2x – y) = 3x + 2y.
2. Знайдіть значення виразу (–2,4 + 0,4)4.
А) –8; Б) 8; В) 16; Г) –16.
3. Спростіть вираз (−a 6)3æ(−a7 )4.
А) a20; В) a46;
Б) –a20; Г) –a46.
4. Виконайте піднесення до степеня: (0,3a 4)2.
А) 0,9a6; В) 0,09a6;
Б) 0,9a8; Г) 0,09a8.
5. Який із наведених виразів є одночленом?
А) 0,4x + y; В) 0,4xy;
Б) 0,4x – y; Г) немає жодного.
6. Якому з одночленів дорівнює вираз 0,7a 3b2æ![]() a 2b4 ?
a 2b4 ?
А) 7a5b6; Б) 7a6b8; В) 0,1a5b6; Г) 0,1a6b8.
7. Квадратом якого з наведених одночленів є вираз ![]() b64c100 ?
b64c100 ?
![]()
![]() А) −1 b8c10; Б) b32c50; В) b8c10; Г) −1 b32c10.
А) −1 b8c10; Б) b32c50; В) b8c10; Г) −1 b32c10.
22
8. Відомо, що m < 0 і n < 0. Порівняйте з нулем значення виразу m5n6.
А) m5n6 = 0; В) m5n6 < 0;
Б) m5n6 > 0; Г) неможливо з’ясувати.
9. Зведіть подібні члени многочлена 2x2 + 6xy – 5x2 – 9xy + 3y2.
А) –3xy; В) 3x2y2;
Б) –3x2 – 3xy + 3y2; Г) 3x2 + 3xy + 3y2.
10. Знайдіть різницю многочленів x2 – 3x – 4 і x – 3x2 – 2.
А) 4x2 – 4x – 2; В) –2x2 – 2x – 6;
Б) –2x2 – 4x – 2; Г) 4x2 – 4x – 6.
11. Який із наведених виразів набуває тільки від’ємних значень? А) x6 + 4; Б) x6 – 4; В) –x6 + 4; Г) –x6 – 4.
12. Якого найменшого значення набуває вираз (x – 7)2 + 2?
А) 2; Б) 7; В) 5; Г) 9.
![]() 10. Множення одночлена на многочлен
10. Множення одночлена на многочлен
Помножимо одночлен 2x на многочлен 3x 2y 5. Для цього запишемо добуток 2x (3x 2y 5). Розкриємо дужки, застосувавши розподільну властивість множення. Маємо:
2x (3x 2y 5) 2xæ3x 2xæ2y 2xæ5 6x 2 4xy 10x.
![]() Отриманий многочлен 6x2 + 4xy – 10x є добутком одночлена 2x і многочлена 3x 2y 5.
Отриманий многочлен 6x2 + 4xy – 10x є добутком одночлена 2x і многочлена 3x 2y 5.
Добуток одночлена й многочлена завжди можна подати у вигляді многочлена.
Щоби помножити одночлен на многочлен, потрібно помножити цей одночлен на кожний член многочлена й отримані добутки додати.
При множенні одночлена й многочлена виконується переставна властивість множення. Тому наведене правило дає змогу множити многочлен на одночлен.
![]() ПРИКЛАД 1 Спростіть вираз 6x (x – 1) – 3 (2x2 – 3x + 4). Розв’язання. Маємо:
ПРИКЛАД 1 Спростіть вираз 6x (x – 1) – 3 (2x2 – 3x + 4). Розв’язання. Маємо:
6x (x – 1) – 3 (2x2 – 3x + 4) =
![]() = 6x 2 6x 6x 2 9x 12 3x 12.
= 6x 2 6x 6x 2 9x 12 3x 12. ¤
![]()
![]() ПРИКЛАД 2 Розв’яжіть рівняння 0,5x (3 + 4x) = 2x (x – 2) – 11.
ПРИКЛАД 2 Розв’яжіть рівняння 0,5x (3 + 4x) = 2x (x – 2) – 11.
Розв’язання. Маємо:
1,5x + 2x2 = 2x2 – 4x – 11;
1,5x + 2x2 – 2x2 + 4x = –11;
![]() 5,5x = –11; x = –2. Відповідь: –2.
5,5x = –11; x = –2. Відповідь: –2. ¤
![]() ПРИКЛАД 3 Розв’яжіть рівняння 5x 4 x 3 2.
ПРИКЛАД 3 Розв’яжіть рівняння 5x 4 x 3 2.
12 8
Розв’язання. Помноживши обидві частини даного рівняння на число 24, яке є найменшим спільним знаменником дробів, що містить це рівняння, отримуємо:
5x 4 x 3 æ24 2æ24.
12 8
![]() Звідси 24æ24æx 3 48;
Звідси 24æ24æx 3 48;
8
2 (5x + 4) – 3 (x + 3) = 48;
10x + 8 – 3x – 9 = 48;
![]() 7x – 1 = 48; x = 7. Відповідь: 7.
7x – 1 = 48; x = 7. Відповідь: 7. ¤
ПРИКЛАД 4 Доведіть, що при будь-якому значенні змінної a значення виразу 3a (a2 – 4) – 2a2 (1,5a + 4a4) + 6 (2a – 1) є від’ємним числом.
Розв’язання. 3a (a2 – 4) – 2a2 (1,5a + 4a4) + 6 (2a – 1) = = 3a3 – 12a – 3a3 – 8a6 + 12a – 6 = –8a6 – 6.
![]() Вираз –8a6 при будь-якому значенні a набуває недодатного значення. Отже, значення виразу –8a6 – 6 є від’ємним числом при будь-якому значенні a.
Вираз –8a6 при будь-якому значенні a набуває недодатного значення. Отже, значення виразу –8a6 – 6 є від’ємним числом при будь-якому значенні a. ¤
|
Розв’язання. Нехай неповна частка при діленні m на 6 дорівнює a, а при діленні n на 4 дорівнює b. Тоді m = 6a + 5, n = 4b + 2. Отже, 2m + 3n = 2 (6a + 5) + 3 (4b + 2) = = 12a + 10 + 12b + 6 = 12a + 12b + 16. Кожний доданок отриманої суми ділиться націло на 4, тому й сума ділиться націло на 4.
|

|
391.° Виконайте множення: |
|
|
1) a (a – b); |
3) –c (4 + c); |
|
2) m (m + n – 4); 392.° Виконайте множення: |
4) –a2 (a2 – a + 1). |
|
1) m (n – 3); |
3) –m (m – 6); |
|
2) x (y – z + 4); |
4) –a (a3 – b + c). |
393.° Перетворіть у многочлен добуток:
|
1) 3x (2x + 5); |
7) (4y 3 6y 7)æ( 1,2y 3); |
|
2) 4x (x 2 −8x −2); |
8) 0,4x 2y (3xy 2 5xy 13x 2y 3); |
|
3) 2a (a 2 a 3); |
9) (2,3a 3b−1,7b4 −3,5b)æ(−10a 2b); |
|
4) 5b2 (3b2 7b 10); |
10) 4pk 3 (3p2k p 4k 2); |
5) mn (m 2n −n 3); 11) ![]() mn 2 (6m 1,8n 9);
mn 2 (6m 1,8n 9);
6) ![]()
![]() 2ab (a3 3a 2b b2); 12) 1cd 7 c5 7 c2d 7d 10 .
2ab (a3 3a 2b b2); 12) 1cd 7 c5 7 c2d 7d 10 .
8 24
|
394.° Виконайте множення: |
|
|
1) 3x (4x 2 −x); |
4) x 3 (x 5 x 2 7x 1); |
|
2) −5a 2 (a 2 −6a −3); |
5) 2c2d 4 (4c2 c3d 5d 4); |
|
3) (8b2 10b 2)æ0,5b; 395.° Спростіть вираз: |
6) (5m 3n −8mn 2 −2n 6)æ(−4m 2n 8). |
|
1) 8x – 2x (3x + 4); |
5) 2m (m – 3n) + m (5m + 11n); |
|
2) 7a 2 3a (9 5a); |
6) 8x (x 2 y 2) 9x (x 2 y 2); |
|
3) 6x (4x 7) 12 (2x 2 1); |
7) 5b3 (2b −3) −2,5b3 (4b −6); |
|
4) c (c2 1) c2 (c 1); 396.° Спростіть вираз: |
8) x (5x 2 6x 8) 4x (2 2x x 2). |
|
1) 7x (x – 4) – x (6 – x); |
3) xy (2x 11y) x (xy 14y 2); |
2) 5ab (4a 3b) 10a 2 (2b 4); 4) 5c3 (4c −3) −2c2 (8c2 −12).
397.° Спростіть вираз і знайдіть його значення:
1) 3x (2x – 5) – 8x (4x – 3), якщо x = –1;
2) 2x (14x 2 x 5) 4x (2,5 3x 7x 2), якщо x = 7; 3) 8ab (a2 −2b2) −7a (a2b−3b3), якщо a = –3, b = 2.
398.° Спростіть вираз і знайдіть його значення:
1) 6x (6x – 4) + 9x (3 – 4x), якщо x ![]() ;
;
2) 2m (m – n) – n (3m – n) – n (n + 6), якщо m = –4, n = 0,5.
399.° Розв’яжіть рівняння:
1) 5x (3x – 2) – 15x (4 + x) = 140;
2) 1,2x (4 + 5x) = 3x (2x + 1) – 9;
3) 6x (7x – 8) – 2x (21x – 6) = 3 – 30x;
4) 12x – 3x (6x – 9) = 9x (4 – 2x) + 3x;
5) 7x 2 x (7x 5) 2 (2,5x 1) 3 0; 6) 8 (x 2 4) 4x (3,5x 7) 20x 6x 2.
400.° Знайдіть корінь рівняння:
1) 0,4x (5x – 6) + 7,2 = 2x (x + 0,6);
2) x (3x 2) 9 (x 2 7x) 6x (10 x); 3) 12 (x 3 2) 7x (x 2 1) 5x 3 2x 6.
401.• Доведіть тотожність:
1) ab (b c) ac (c b) a (b2 3bc c2) abc;
2) 4a (a b) a (3a 4b) 8ab a 2;
3) a (a + 2b) + b (a + b) = b (2a + b) + a (a + b); 4) a (b + c – bc) – b (a + c – ac) = (a – b) c.
402.• Доведіть тотожність:
1) a (a b) b (a b) a 2 b2;
2) b (a – b) + b (b + c) = b (a + b) – b (b – c).
403.• Доведіть, що коли:
1) a + b + c = 0, то a (bc – 1) + b (ac – 1) + c (ab – 1) = 3abc; 2) a 2 b2 c2, то c (ab – c) – b (ac – b) – a (bc – a) + abc = 0.
404.• Доведіть, що значення виразу
x (12x 11) x 2 (x 2 8) x (11 4x x 3)
не залежить від значення змінної.
405.• Доведіть, що значення виразу
6x (x 3) 9 ![]() x 2 2x 7
x 2 2x 7
не залежить від значення змінної.
406.• Доведіть, що при будь-яких значеннях x значення виразу 4 (x 2 2x 4) 0,5x (6x 16) є додатним числом.
407.• Доведіть, що вираз 3x 2 (3 4x) 6x (1,5x 2x 2 x 3) набуває недодатних значень при всіх значеннях x.
408.• Доведіть, що вираз 7a 4 (a 3) a 3 (21a 7a 2 3a 5) набуває невід’ємних значень при всіх значеннях a.
409.• Замініть зірочки такими одночленами, щоб утворилася тотожність:
1) *æ(a b c) abc b2c bc2; 3) 3a 2 (* *) 6a 3 15a 4.
2) *æ(ab b2) a 3b a 2b2;
410.• Замініть зірочки такими одночленами, щоб утворилася тотожність:
1) (x y)æ* x 2y 2 x 3y; 3) (1,4x *)æ3x * 0,6x 3; 2) ( 9x 2 *)æy * y 4; 4) * (* x 2y 5 5y 6) 8x 3y 3 5x 3y 8 *.
411.• Спростіть вираз:
1) 15aæa 4 12a 2æ5 2a ;
3 6
2) 24c3æc2 2c 3 18c2æc3 c2 2;
8 9
3) 34xæx −y −45yæx −2y − y (6y −5x).
17 15
412.• Спростіть вираз:
1) ![]() 6b2æ20bæ3b 2b3 ;
6b2æ20bæ3b 2b3 ;
4
2) 14mæm n m næ16n 2 (m 2 n 2).
7 8
413.• Розв’яжіть рівняння:
1) x 7 x 2; 5) 6x 7 3x 1 11 x ;
4 6 5 6 15
2) x 6 x 7 4; 6) 5x 3 4x 3 x 1;
![]() 9 6
9 6
![]() x 1; 7) 8x 5 4x 3 2 9x 3;
x 1; 7) 8x 5 4x 3 2 9x 3;
3)
6 8 3 3 4 2
4) 3x 2x 3 x 6; 8) 8x 2 3x 6x 2 1 1.
2 3 16 12
414.• Знайдіть корінь рівняння:
![]() 1) x; 3) 2x 3 5x 13 5 2x 6;
1) x; 3) 2x 3 5x 13 5 2x 6;
3 6 2
2x 1 3x 1 2; 4) 4x 2 5x 10 2x 2 5.
2)
6 7 14 7
415.• При якому значенні змінної значення виразу 8y (y – 7) на 15 більше за значення виразу 2y (4y – 10,5)?
416.• Довжина прямокутника в 3 рази більша за його ширину. Якщо ширину прямокутника зменшити на 6 см, то його площа зменшиться на 144 см2. Знайдіть початкову ширину прямокутника.
417.• Ширина прямокутника на 8 см менша від його довжини. Якщо довжину прямокутника збільшити на 6 см, то його площа збільшиться на 72 см2. Знайдіть периметр даного прямокутника.
418.• За 3 дні туристка пройшла 108 км. За другий день вона пройшла на 6 км більше, ніж за перший, а за третій — ![]() відстані, пройденої за два перших дні. Скільки кілометрів туристка пройшла за кожний із цих днів?
відстані, пройденої за два перших дні. Скільки кілометрів туристка пройшла за кожний із цих днів?
419.• Три бригади робітників виготовили за зміну 80 деталей. Перша бригада виготовила на 12 деталей менше, ніж друга, а третя — ![]() кількості деталей, виготовлених першою та другою бригадами разом. Скільки деталей виготовила кожна бригада?
кількості деталей, виготовлених першою та другою бригадами разом. Скільки деталей виготовила кожна бригада?
420.•• Спростіть вираз:
1) x n 1 (x n 6 1) x n 2 (x n 5 x 3); 2) x n 2 (x 2 3) x n (x n 2 3x 2 1), де n — натуральне число.
421.•• Спростіть вираз:
1) x n (x n 4 2x) x (3x n x 2n 3);
2) x (4x n 1 2x n 4 7) x n 2 (4 2x 3 x n), де n — натуральне число.
422.* Остача при діленні натурального числа a на 3 дорівнює 1, а остача при діленні натурального числа b на 9 дорівнює 7. Доведіть, що значення виразу 4a + 2b ділиться націло на 3.
423.* Остача при діленні натурального числа m на 5 дорівнює 3, а остача при діленні натурального числа n на 3 дорівнює 2. Доведіть, що значення виразу 3m + 5n не ділиться націло на 15.
![]()
424. У магазині проводиться акція: при купівлі двох однакових коробок цукерок третя така сама коробка надається безкоштовно. Яку найбільшу кількість коробок цукерок можна придбати, маючи 1500 грн, якщо одна коробка коштує 65 грн?
425. Квиток на проїзд у міжміському автобусі для дорослої людини коштує 200 грн, а ціна квитка для школяра чи школярки становить 60 % від ціни квитка для дорослої людини. Група складається з 22 школярів і школярок та 3 дорослих людей. Скільки коштують квитки на проїзд для всієї групи?
426. Три найбільших лимани України — Дніпровсько-Бузький, Дністровський і Сасик (Кундук) знаходяться на узбережжі Чорного моря. Їхня загальна площа 1364,8 км2. Площа Дністровського лиману у 2![]() раза менша від площі Дніпровсько-Бузького, а площа лиману Сасик становить 25,6 % площі ДніпровськоБузького. Знайдіть площу кожного лиману.
раза менша від площі Дніпровсько-Бузького, а площа лиману Сасик становить 25,6 % площі ДніпровськоБузького. Знайдіть площу кожного лиману.
427. Першого дня Надія прочитала ![]() сторінок книжки, другого —
сторінок книжки, другого —
64 % решти, а третього — 54 сторінки, що залишилися. Скільки сторінок у книжці?
428. Яка ймовірність того, що при киданні грального кубика випаде:
1) непарне число;
2) число, яке ділиться націло на 3;3) число, яке не ділиться націло на 3?
429. Велосипедист проїхав першу половину шляху за 3 год, а другу — за 2,5 год, оскільки збільшив швидкість на 3 км/год. Яку відстань проїхав велосипедист?
430. На одному складі було 184 т мінерального добрива, а на другому — 240 т. Перший склад відпускає щодня по 15 т добрива, а другий — по 18 т. Через скільки днів маса добрива, що залишиться на першому складі, становитиме ![]() маси добрива, що залишиться на другому складі?
маси добрива, що залишиться на другому складі?
 УЧИМОСЯ РОБИТИ НЕСТАНДАРТНІ КРОКИ
УЧИМОСЯ РОБИТИ НЕСТАНДАРТНІ КРОКИ
431. У волейбольному турнірі, який проходив в одне коло (тобто кожна команда грала з кожною іншою один раз), 20 % усіх команд не виграли жодної гри. Скільки команд узяло участь у цьому турнірі? (Примітка. У волейболі нічиїх не буває, обов’язково одна команда виграє, а друга програє.)
![]() 11. Множення многочлена на многочлен
11. Множення многочлена на многочлен
Покажемо, як помножити многочлен на многочлен, на прикладі добутку (a b) (x y z). Позначимо другий множник буквою c.
Тоді отримуємо:
(a b) (x y z) (a b) c ac bc.
Тепер у вираз ac +bc підставимо замість c многочлен x − y −z. Запишемо: ac bc a (x y z) b (x y z) ax ay az bx by bz.
Отриманий многочлен і є шуканим добутком.
Цей самий результат можна отримати, якщо добуток знаходити за схемою:
![]()
Вона роз’яснює таке правило:
щоби помножити многочлен на многочлен, можна кожний член одного многочлена помножити на кожний член другого й отримані добутки додати.
Отже, при множенні многочлена на многочлен завжди отримуємо многочлен.
![]() ПРИКЛАД 1 Спростіть вираз (3x – 4) (2x + 3) – (x – 2) (x + 5).
ПРИКЛАД 1 Спростіть вираз (3x – 4) (2x + 3) – (x – 2) (x + 5).
Розв’язання. Маємо:
(3x – 4) (2x + 3) – (x – 2) (x + 5) =
= 6x2 + 9x – 8x – 12 – (x2 + 5x – 2x – 10) =
![]() 6x 2 9x 8x 1..2. x 2 5x 2x 1..0. 5x 2 2x 2.
6x 2 9x 8x 1..2. x 2 5x 2x 1..0. 5x 2 2x 2. ¤
![]()
ПРИКЛАД 2 Подайте у вигляді многочлена вираз
(a + 2) (a – 5) (a + 3).
Розв’язання. (a + 2) (a – 5) (a + 3) = (a2 – 5a + 2a – 10) (a + 3) =
= (a2 – 3a – 10) (a + 3) a 3 3a 2 3a 2 9a 10a 30
= a3 – 19a – 30. ![]()
![]() ПРИКЛАД 3 Знайдіть чотири послідовних натуральних числа таких, що добуток третього й четвертого з них на 38 більший за добуток першого та другого.
ПРИКЛАД 3 Знайдіть чотири послідовних натуральних числа таких, що добуток третього й четвертого з них на 38 більший за добуток першого та другого.
Розв’язання. Нехай менше із цих чисел дорівнює x, тоді три наступних за ним числа дорівнюватимуть x + 1, x + 2, x + 3. Оскільки за умовою добуток (x + 2) (x + 3) на 38 більший за добуток x (x + 1), то маємо:
(x + 2) (x + 3) – x (x + 1) = 38.
Звідси x2 + 2x + 3x + 6 – x2 – x = 38; 4x = 38 – 6; x = 8.
![]() Отже, шуканими числами є 8, 9, 10 і 11.
Отже, шуканими числами є 8, 9, 10 і 11. ¤
![]() ПРИКЛАД 4 Доведіть, що значення виразу
ПРИКЛАД 4 Доведіть, що значення виразу
(n + 39) (n – 4) – (n + 31) (n – 3)
кратне 7 при всіх натуральних значеннях n. Розв’язання. Виконаємо перетворення:
(n + 39) (n – 4) – (n + 31) (n – 3) =
= n2 – 4n + 39n – 156 – (n2 – 3n + 31n – 93) =
![]()
![]() n 2 4n 39n 1.5..6 n 2 3n 31n 9..3. 7n 63 7(n 9).
n 2 4n 39n 1.5..6 n 2 3n 31n 9..3. 7n 63 7(n 9).
Даний вираз подано у вигляді добутку двох множників, один з яких дорівнює 7, а другий набуває тільки цілих значень. Отже, при будь-якому натуральному n значення даного виразу ділиться

¤
 ВПРАВИ
ВПРАВИ
|
432.° Виконайте множення: |
|
|
1) (a – 2) (b + 5); |
7) (–2m – 3) (5 – m); |
|
2) (m + n) (p – k); |
8) (5x2 – x) (6x2 + 4x); |
|
3) (x – 8) (x + 4); |
9) (–c – 4) (c3 + 3); |
|
4) (x – 10) (x – 9); |
10) (x – 5) (x2 + 4x – 3); |
|
5) (c + 5) (c + 8); |
11) (2a + 3) (4a2 – 4a + 3); |
|
6) (3y + 1) (4y – 6); |
12) a (5a – 4) (3a – 2). |
433.° Перетворіть у многочлен вираз:
1) (a + b) (c – d); 6) (3y – 5) (2y – 12);
2) (x – 6) (x – 4); 7) (2x2 – 3) (x2 + 4);
3) (a – 3) (a + 7); 8) (x – 6) (x2 – 2x + 9);
4) (11 – c) (c + 8); 9) (5x – y) (2x2 + xy – 3y2); 5) (d + 13) (2d – 1); 10) b (6b + 7) (3b – 4).
434.° Спростіть вираз:
1) (x + 2) (x + 11) – 2x (3 – 4x);
2) (a + 5) (a – 2) + (a – 4) (a + 6); 3) (y – 9) (3y – 1) – (2y + 1) (5y – 7); 4) (4x – 1) (4x – 3) – (2x – 10) (8x + 1).
435.° Спростіть вираз:
1) (a – 2) (a – 1) – a (a + 1);
2) (b – 5) (b + 10) + (b + 6) (b – 8); 3) (2c + 3) (3c + 2) – (2c + 7) (2c – 7);
4) (3d + 5) (5d – 1) – (6d – 3) (2 – 8d).
436.° Спростіть вираз і знайдіть його значення: 1) (x + 2) (x – 5) – (x – 3) (x + 4), якщо x = –5,5; 2) (y + 9) (y – 2) + (3 – y) (6 + 5y), якщо y 1![]() .
.
437.° Спростіть вираз і знайдіть його значення:
1) (a + 3) (a – 10) – (a + 7) (a – 4), якщо a = –0,01; 2) (8c + 12) (3c – 1) + (3c + 2) (–5c – 6), якщо c =1![]() .
.
438.• Розв’яжіть рівняння:
1) (2x – 3) (4x + 3) – 8x2 = 33;
2) (2x – 6) (8x + 5) + (3 – 4x) (3 + 4x) = 55;
3) 21x 2 (3x 7) (7x 3) 37;
4) (x + 1) (x + 2) – (x – 3) (x + 4) = 12;
5) (–4x + 1) (x – 1) – x = (5 – 2x) (2x + 3) – 17.
439.• Розв’яжіть рівняння:
1) (2x – 1) (15 + 9x) – 6x (3x – 5) = 87;
2) (14x – 1) (2 + x) = (2x – 8) (7x + 1); 3) (x + 10) (x – 5) – (x – 6) (x + 3) = 16; 4) (3x + 7) (8x + 1) = (6x – 7) (4x – 1) + 93x.
440.• Виконайте множення:
|
1) (x + 2) (x – 1) (x – 4); |
4) (a + 2b – c) (a – 3b + 2c); |
|
2) (2x + 1) (x + 5) (x – 6); |
5) (a b) (a 3 a 2b ab2 b3); |
|
3) (x 2 2x 3) (x 2 2x 3); |
6) (x 1) (x 4 x 3 x 2 x 1). |
441.• Перетворіть у многочлен вираз:
1) (a + 1) (a – 2) (a – 3); 3) (a 2 2a 1) (a 2 3a 2);
2) (3a – 2) (a + 3) (a – 7); 4) (a 1) (a 4 a 3 a 2 a 1).
442.• Замініть степінь добутком, а потім добуток перетворіть у многочлен:
1) (a +5)2; 3) (a +b+ c)2; 2) (4 −3b)2; 4) (a −b)3.
443.• Доведіть, що при будь-якому значенні змінної значення виразу (x + 3) (x2 – 4x + 7) – (x2 – 5) (x – 1) дорівнює 16.
444.• Доведіть, що при будь-якому значенні змінної значення виразу (x 3) (x 2 7) (x 2) (x 2 x 5) дорівнює –11.
445.• Задумали чотири натуральних числа. Друге число на 1 більше за перше, третє — на 5 більше за друге, а четверте — на 2 більше за третє. Знайдіть ці числа, якщо відношення першого числа до третього дорівнює відношенню другого числа до четвертого.
446.• Задумали три натуральних числа. Друге число на 4 більше за перше, а третє — на 6 більше за друге. Знайдіть ці числа, якщо відношення першого числа до другого дорівнює відношенню другого числа до третього.
447.• Знайдіть чотири послідовних натуральних числа таких, що добуток четвертого й другого із цих чисел на 17 більший за добуток третього та першого.
448.• Знайдіть три послідовних натуральних числа таких, що добуток другого та третього із цих чисел на 50 більший за квадрат першого.
449.• Сторона квадрата на 3 см менша від однієї зі сторін прямокутника та на 5 см більша за його другу сторону. Знайдіть сторону квадрата, якщо його площа на 45 см2 більша за площу даного прямокутника.
450.• Периметр прямокутника дорівнює 60 см. Якщо одну його сторону зменшити на 5 см, а другу збільшити на 3 см, то його площа зменшиться на 21 см2. Знайдіть сторони даного прямокутника.
451.• Довжина прямокутника на 2 см більша за його ширину. Якщо довжину збільшити на 2 см, а ширину зменшити на 4 см, то площа прямокутника зменшиться на 40 см2. Знайдіть початкові довжину та ширину прямокутника.
452.• Доведіть тотожність:
1) x 2 8x 7 (x 1) (x 7);
2) y 2 (y 7) (y 2) y 4 5y 3 14y 2;
3) a3 – 8 = (a – 2) (a2 + 2a + 4);
4) (a – 1) (a + 1) (a2 + 1) = a4 – 1;
5) (a 4 a 2 1) (a 4 a 2 1) a 8 a 4 1.
453.• Доведіть тотожність:
1) 3a 2 10a 3 3(a 3) a ![]() ;
;
2) (a 1) (a 2 5a 6) (a 2 3a 2) (a 3); 3) (a 1) (a 4 a 3 a 2 a 1) a 5 1.
454.• Чи при всіх натуральних значеннях n значення виразу (n + 9) (n + 11) – (n + 3) (n + 5) кратне 12?
455.• Чи при всіх натуральних значеннях n значення виразу (n + 29) (n + 3) – (n + 7) (n + 1) кратне 8?
456.• Замініть зірочки такими одночленами, щоб утворилася тотожність:
1) (a 2) (* 6) a 2 * *;
2) (2a + 7) (a – *) = * + * – 14.
457.• Замініть зірочки такими одночленами, щоб утворилася тотожність:
1) (x 3) (* 5) 3x 2 * *; 2) (x – 4) (x + *) = * + * + 24.
458.•• Вибрали деякі чотири послідовних натуральних числа й обчислили різницю добутку другого й третього із цих чисел і добутку першого та четвертого. Чи залежить ця різниця від вибору чисел?
459.•• Вибрали деякі три послідовних натуральних числа й обчислили різницю квадрата другого із цих чисел і добутку першого та третього. Чи залежить ця різниця від вибору чисел?
![]()
460.•• Доведіть, що значення виразу abæba −ab ділиться націло на 10 незалежно від значень a і b.
461.•• Остача при діленні натурального числа x на 6 дорівнює 3, а остача при діленні натурального числа y на 6 дорівнює 2. Доведіть, що добуток чисел x і y ділиться націло на 6.
462.•• Остача при діленні натурального числа a на 8 дорівнює 3, а остача при діленні натурального числа b на 8 дорівнює 7. Доведіть, що остача при діленні добутку чисел a і b на 8 дорівнює 5.
463.•• Остача при діленні натурального числа m на 11 дорівнює 9, а остача при діленні натурального числа n на 11 дорівнює 5. Доведіть, що остача при діленні добутку чисел m і n на 11 дорівнює 1.
464.•• Доведіть, що коли ab + bc + ac = 0, то
(a b) (a c) (b c) (b a) (c a) (c b) a 2 b2 c2.
![]()
465. Податок на доходи фізичних осіб становить 18 % від заробітної плати. Після утримання податку інженер отримав 9840 грн. Яка заробітна плата була йому нарахована?
466. Після подорожчання на 20 % костюм став коштувати 2760 грн. Якою була ціна костюма до подорожчання?
467. Дві робітниці виготовили разом 108 деталей. Перша робітниця працювала 5 год, а друга — 3 год. Скільки деталей виготовляла щогодини кожна робітниця, якщо разом за 1 год вони виготовляють 26 деталей?
¿ 468. Змішали 72 г 5 %-го розчину солі та 48 г 15 %-го розчину солі. Знайдіть відсотковий вміст солі в утвореному розчині.
469. Розв’яжіть рівняння:
![]()
1) 1x 2x x6; 2) x4 x8 1x2.
470. Доведіть тотожність:
1) 1816n =128næ912n; 2) 758n =2254næ6252n, де n — натуральне число.
471. (Старовинна грецька задача.) Демохар[3] четверту частину життя прожив хлопчиком, п’яту частину — юнаком, третю частину — зрілою людиною та 13 років — у літах. Скільки років прожив Демохар?
![]() ГОТУЄМОСЯ ДО ВИВЧЕННЯ НОВОЇ ТЕМИ
ГОТУЄМОСЯ ДО ВИВЧЕННЯ НОВОЇ ТЕМИ
472. Обчисліть, використовуючи розподільну властивість множення:
1) 4,8æ2,9 +4,8æ7,1; 3) 3![]() æ0,3 0,3æ1
æ0,3 0,3æ1![]() 0,3æ1
0,3æ1![]() .
.
2) 3![]() æ
æ![]() −2
−2![]() æ
æ![]() ;
;
|
473. Розв’яжіть рівняння: |
|
|
1) x (x + 4) = 0; 2) (x – 6) (x + 9) = 0; |
3) (3x + 5) (10 – 0,4x) = 0. |
Поновіть у пам’яті зміст пп. 11, 13 на с. 268, 269.
 УЧИМОСЯ РОБИТИ НЕСТАНДАРТНІ КРОКИ
УЧИМОСЯ РОБИТИ НЕСТАНДАРТНІ КРОКИ
474. У кожній клітинці дошки розміром 5 × 5 клітинок сидить жук. У деякий момент усі жуки переповзають на сусідні (по горизонталі або вертикалі) клітинки. Чи обов’язково при цьому залишиться порожня клітинка?
![]() 12. Розкладання многочлена на множники.
12. Розкладання многочлена на множники.
Винесення спільного множника за дужки
Помножимо многочлен 2x – 1 на многочлен x + 1. Маємо:
(2x 1) (x 1) 2x 2 2x x 1 2x 2 x 1.
Отримали тотожність (2x 1) (x 1) 2x 2 x 1, яку можна записати ще й так: 2x 2 x 1 (2x 1) (x 1).
Про цей запис говорять, що многочлен 2x 2 x 1 розклали на множники 2x – 1 і x + 1.
Узагалі, подання многочлена у вигляді добутку кількох многочленів називають розкладанням многочлена на множники.
Розкладання многочлена на множники є ключем до розв’язування багатьох задач. Наприклад, кожне з рівнянь 2x – 1 = 0 і x + 1 = 0 розв’язати дуже легко, а ось рівняння 2x 2 x 1 0 ви поки що розв’язувати не вмієте. Проте якщо скористатися розкладанням многочлена 2x 2 x 1 на множники, то рівняння 2x 2 x 1 0 можна записати так:
(2x 1) (x 1) 0.
Звідси 2x – 1 = 0 або x + 1 = 0. Шуканими коренями є числа 0,5 і –1.
Отже, розкладання многочлена на множники дозволило звести розв’язання складного рівняння до розв’язання двох простіших.
Існує чимало способів розкладання многочлена на множники. Найпростіший із них — винесення спільного множника за дужки.
Це перетворення вам уже відоме. Наприклад, у 6 класі значення виразу 1,62æ1,08 −0,08æ1,62 знаходили так:
1,62æ1,08 0,08æ1,62 1,62 (1,08 0,08) 1,62.
Тут використано розподільну властивість множення відносно додавання c (a b) ac bc, прочитану справа наліво: ac bc c (a b).
Скористуємося цією ідеєю, розв’язуючи такі приклади.
![]() ПРИКЛАД 1 Розкладіть на множники:
ПРИКЛАД 1 Розкладіть на множники:
1) a2b2 + ab3; 2) 8a2b2 – 12ab3; 3) 10a8 – 5a5.
Розв’язання. 1) Одночлени a2b2 і ab3 містять такі спільні множники: a, b, ab, b2 і ab2. Будь-який із цих множників можна винести за дужки. Але зазвичай спільний множник вибирають такий, щоб члени многочлена, який залишається в дужках, не мали спільного буквеного множника. Такі міркування підказують, що потрібно винести за дужки спільний множник ab2: a2b2 + ab3 = ab2 (a + b).
Щоби перевірити, чи правильно розкладено многочлен на множники, треба перемножити отримані множники.
2) Якщо коефіцієнти многочлена — цілі числа, то за дужки зазвичай виносять найбільший спільний дільник модулів цих коефіцієнтів (у нашому прикладі це число 4):
8a2b2 – 12ab3 = 4ab2 (2a – 3b).
3) ![]() Маємо: 10a8 – 5a5 = 5a5 (2a3 – 1).
Маємо: 10a8 – 5a5 = 5a5 (2a3 – 1). ¤
![]() ПРИКЛАД 2 Подайте у вигляді добутку многочленів вираз:
ПРИКЛАД 2 Подайте у вигляді добутку многочленів вираз:
1) a (m – 3) + b (m – 3); 3) 6x (x – 7) – (x – 7)2.
2) x (c – d) + y (d – c);
Розв’язання. 1) У даному випадку спільним множником є многочлен m – 3: a (m – 3) + b (m – 3) = (m – 3) (a + b).
2) Маємо:
x (c d) y (d c) x (c d) yæ( 1)æ(c d) x (c d) y (c d) (c d) (x y).
3) Маємо:
6x (x – 7) – (x – 7)2 = (x – 7) (6x – (x – 7)) =
![]() = (x – 7) (6x – x + 7) = (x – 7) (5x + 7). ¤
= (x – 7) (6x – x + 7) = (x – 7) (5x + 7). ¤
![]() ПРИКЛАД 3 Винесіть за дужки спільний множник у виразі (12x – 18y)2.
ПРИКЛАД 3 Винесіть за дужки спільний множник у виразі (12x – 18y)2.
Розв’язання. Маємо: (12x – 18y)2 = (6 (2x – 3y))2 = 62 (2x – 3y)2 =
![]() = 36 (2x – 3y)2. ¤
= 36 (2x – 3y)2. ¤
![]() ПРИКЛАД 4 Розв’яжіть рівняння:
ПРИКЛАД 4 Розв’яжіть рівняння:
1) 4x2 – 12x = 0; 2) (3x – 7) (x + 4) + (x – 1) (x + 4) = 0.
Розв’язання. 1) Розклавши ліву частину рівняння на множники та застосувавши умову, за якої добуток дорівнює нулю, отримуємо:
4x (x – 3) = 0; x = 0 або x – 3 = 0; x = 0 або x = 3. Відповідь: 0; 3.
2) ![]() (3x – 7) (x + 4) + (x – 1) (x + 4) = 0; (x + 4) (3x – 7 + x – 1) = 0; x + 4 = 0 або 4x – 8 = 0; x = –4 або x = 2. Відповідь: –4; 2. ¤
(3x – 7) (x + 4) + (x – 1) (x + 4) = 0; (x + 4) (3x – 7 + x – 1) = 0; x + 4 = 0 або 4x – 8 = 0; x = –4 або x = 2. Відповідь: –4; 2. ¤
![]() ПРИКЛАД 5 Доведіть, що значення виразу: 1) 87 – 49 ділиться націло на 14; 2) 203 – 44 ділиться націло на 121.
ПРИКЛАД 5 Доведіть, що значення виразу: 1) 87 – 49 ділиться націло на 14; 2) 203 – 44 ділиться націло на 121.
Розв’язання. 1) Подамо вирази 87 і 49 у вигляді степенів з основою 2 та винесемо за дужки спільний множник. Отримуємо:
87 4 9 (23)7 (22)9 221 218 218 (23 1) 218æ(8 1)
=218æ7 = 217 æ2æ7 = 217 æ14.
Отже, даний вираз дорівнює добутку двох натуральних чисел, одним з яких є 14. Звідси випливає, що значення виразу 87 – 49 ділиться націло на 14.
2) Маємо: 203 4 4 (5æ4)3 4 4 53æ43 4 4 43 (53 4) 43 (125 4) 43æ121.
![]()
![]() Отже, значення даного виразу ділиться націло на 121. ¤ ПРИКЛАД 6 При якому значенні a рівняння (x + 2) (x + a) –
Отже, значення даного виразу ділиться націло на 121. ¤ ПРИКЛАД 6 При якому значенні a рівняння (x + 2) (x + a) –
– x (x + 1) = 3a + 1 має безліч коренів?
Розв’язання. Маємо:
x2 + ax + 2x + 2a – x2 – x = 3a + 1; ax + x + 2a = 3a + 1; ax + x = a + 1;
(a + 1) x = a + 1.
При a = –1 останнє рівняння набуває вигляду 0x = 0 і має безліч коренів. Зазначимо, що коли a ≠ –1, то рівняння має єдиний корінь x = (a + 1) : (a + 1), який дорівнює 1.  Відповідь: при a = –1.
Відповідь: при a = –1. ¤
|
475.° Розкладіть на множники: |
|
|
1) am + an; 2) 6x – 6y; 3) –cx – cy; 476.° Винесіть за дужки спільний множник: |
4) 7c – 7. |
|
1) 9a + 9b; 2) ab – bc; 3) ax + a; |
4) 4bk + 4bt. |
477.° Закінчіть розкладання многочлена на множники:
1) 4a – 12b = 4 (...; 3) 27a2b + 18ab2 = 9ab (...; 2) x3 – 2x2y = x2 (...; 4) 6x2 + 12x4 – 18x5 = 6x2 (... . 478.° Закінчіть розкладання многочлена на множники:
1) 7m + 3mn = m (...; 3) –m3 – mnp = –m (...; 2) a7 + a4 = a4 (...; 4) x5y – x4y3 + x3y2 = x3y (... .
479.° Винесіть за дужки спільний множник:
|
1) 4b + 16c; 6) x 2 + xy; |
11) 7 p3 −5p; |
|
2) 12x – 15y; 7) 3d 2 −3cd; |
12) 15c2d −3cd; |
|
3) –8a – 18b; 8) 4a 2 +16ab; |
13) 14x 2y +21xy 2; |
|
4) 24x + 30y; 9) a 6 −a 3; |
14) 2x 9 16x 6; |
|
5) 10mx – 15my; 10) b2 +b8; 480.° Розкладіть на множники: |
15) 8a 4b2 −36a 3b7. |
|
1) 3a +6b; 5) 5b – 25bc; |
9) 9x −27x 4; |
|
2) 12m −16n; 6) 14x 2 +7x; |
10) 18y 5 +12y 4; |
|
3) 10ck −15cp; 7) n 10 −n 5; |
11) 56a10b6 −32a 4b8; |
|
4) 8ax + 8a; 8) m 6 +m 7; |
12) 36mn 5 +63m 2n 6. |
481.° Обчисліть, використовуючи винесення спільного множника за дужки:
1) 1732 +173æ27; 2) 214æ314 −2142; 3) 0,43 +0,42æ0,6.
482.° Знайдіть значення виразу:
1) 5162 −516æ513; 2) 0,7 3 +0,7æ0,51; 3) 0,24 −0,23æ1,2.
483.° Обчисліть значення виразу, попередньо розклавши його на множники:
1) 6,32x −x 2, якщо x = 4,32;
2) a 3 + a2b, якщо a = 1,5, b = –2,5; 3) m3p – m2n2, якщо m = 3, p = ![]() , n = –3.
, n = –3.
484.° Знайдіть значення виразу:
1) 0,74x 2 +26x, якщо x = 100; 2) x 2y 3 −x 3y 2, якщо x = 4, y = 5.
485.° Розв’яжіть рівняння:
1) y 2 6y 0; 3) 4m 2 20m 0; 5) 9x 2 6x 0;
2) x 2 x 0; 4) 13x 2 x 0; 6) 12x 0,3x 2 0.
486.° Розв’яжіть рівняння:
1) x 2 x 0; 3) 5x 2 30x 0; 2) p2 15p 0; 4) 14x 2 18x 0.
487.° Закінчіть розкладання на множники:
1) 3a (x – y) + b (x – y) = (x – y) ...;
2) b (c – 2) + (c – 2) = (c – 2) ...;
3) x (y – 6) + z (6 – y) = x (y – 6) – z (y – 6) = ...; 4) m (8 – n) – 5 (n – 8) = m (8 – n) + 5 (... .
488.° Закінчіть розкладання на множники:
1) a (b – c) – (b – c) = (b – c) ...;
2) 2x (3c – y) + 7y (y – 3c) = 2x (3c – y) – 7y (... . 489.° Розкладіть на множники:
|
1) 2x (a + b) + y (a + b); |
7) b (b – 20) + (20 – b); |
|
2) (a – 4) – b (a – 4); |
8) 6a (a – 3b) – 13b (3b – a); |
|
3) 5a (m – n) + 7b (m – n); |
9) (m −9)2 −3 (m −9); |
|
4) 6x (4x + 1) – 11 (4x + 1); |
10) a (a + 5)2 + (a + 5); |
|
5) a (c – d) + b (d – c); |
11) (m2 – 3) – n (m2 – 3)2; |
|
6) x (x – 6) – 10 (6 – x); |
12) 8c (p – 12) + 7d (p – 12)2. |
490.° Подайте вираз у вигляді добутку многочленів:
|
1) c (x – 3) – d (x – 3); |
5) 4x (2x – y) – 5y (y – 2x); |
|
2) m (p – k) – (p – k); |
6) (y 1)2 4y (y 1); |
|
3) m (x – y) – n (y – x); |
7) 10 (a 2 5) (a 2 5)2; |
|
4) x (2 – x) + 4 (x – 2); |
8) (a −2)2 −6 (a −2). |
491.• Розкладіть на множники:
1) 2a5b2 4a 3b 6a 2b3; 4) 9x 3 4x 2 x ; 2) mn 3 5m 2n 2 7m 2n; 5) −6m 4 −8m 5 −2m 6; 3) xy 2 x 2y xy; 6) 42a 4b−28a3b2 −70a5b3.
492.• Винесіть за дужки спільний множник:
1) m 2n +mn +n; 3) 7a 4b3 14a 3b4 21a2b5; 2) 3x 6 6x 5 15x 4; 4) 20b6c5 −45b5c6 −30b5c5.
493.• Знайдіть і виправте помилки в рівностях:
1) 4a + 4 = 4 (a + 4); 3) –5x – 10y = –5 (x – 2y); 2) 6ab – 3b = b (6a – 2b); 4) x 6 x 4 x 2 x 2 (x 3 x 2 x).
494.• Доведіть, що сума будь-якого натурального числа та його квадрата є парним числом.
495.• Розкладіть на множники:
1) a (2a b) (a b) 4a (a b)2;
2) 3m 2 (m 8) 6m (m 8)2;
3) (2a + 3) (a + 5) + (a – 1) (a + 5); 4) (3x + 7) (4y – 1) – (4y – 1) (2x + 10);
5) (5m – n)3 (m + 8n)2 – (5m – n)2 (m + 8n)3.
496.• Подайте у вигляді добутку многочленів вираз:
1) (x – 6) (2x – 4) + (x – 6) (8 – x);
2) (x 2 2) (3y 5) (x 2 2) (y 12);
3) (4a – 3b) (5a + 8b) + (3b – 4a) (2a + b); 4) (p – 9)4 (2p + 1)3 + (p – 9)3 (2p + 1)4.
497.• Розв’яжіть рівняння, використовуючи розкладання на множники:
1) (x – 3) (x + 7) – (x + 7) (x – 8) = 0;
2) (4x – 9) (x – 2) + (1 – x) (x – 2) = 0;
3) 0,2x (x – 5) + 8 (x – 5) = 0;
4) 7 (x 7) (x 7)2 0.
498.• Розв’яжіть рівняння, використовуючи розкладання на множники:
1) (2x – 9) (x + 6) – x (x + 6) = 0;
2) (3x + 4) (x – 10) + (10 – x) (x – 8) = 0;
3) 3 (3x 1)2 4 (3x 1) 0;
4) (9x – 12) – x (9x – 12) = 0.
499.• Винесіть за дужки спільний множник:
|
1) (2x −6)2; |
3) (36x +30y)2; |
5) (6x −9y)3; |
7) (−7a −14ab)2; |
|
2) (5y +5)2; |
4) (2x +4)4; |
6) (a 2 + ab)2; |
8) (3c4 −6c3)4. |
500.• Винесіть за дужки спільний множник:
1) (4x −4y)2; 3) (8m −10n)3; 5) (16x 2y +40xy 2)2; 2) (18a +27b)2; 4) (a 2 −9a)2; 6) (22x 4 −28x 2y 3)5.
501.• Доведіть, що значення виразу:
1) 195 +194 кратне 20; 4) 2æ32006 +5æ32005 +7æ32004 кратне 10;
2) 810 −8 9 −8 8 кратне 11; 5) 27 4 −95 кратне 24; 3) 87 +215 кратне 5; 6) 124 −46 кратне 130.
502.• Доведіть, що значення виразу:
1) 2525 −2524 ділиться націло на 12;
2) 16 4 85 47 ділиться націло на 10;
3) 365 +6 9 ділиться націло на 42; 4) 105 −57 ділиться націло на 7.
503.•• Доведіть, що коли:
1) a + b = 2, то a2b ab2 2ab 0;
2) 3a + 4b = –2, то 12a 3b 16a 2b2 32a 2b 24a 2b.
504.•• Доведіть, що коли:
1) a + b + c = 0, то a3b3c2 a2b4c2 a 2b3c3 0; 2) a 2 b2 2ab 1, то a 6b4 2a5b5 a 4b6 a 4b4.
505.•• Розв’яжіть рівняння:
1) 8x 2 3 (x 4) 12; 3) 4x – 0,2x (x + 20) = x3; 2) 5x3 – x (2x – 3) = 3x; 4) 9x (x 3) (x 4) (x 5) 20.
506.•• Знайдіть корені рівняння:
1) (3x – 2) (3x + 2) – (2x – 5) (8x – 3) = 4x – 19;
2) ![]() (12 x 3)
(12 x 3) ![]() x 2 4.
x 2 4.
507.•• Спростіть вираз, використовуючи винесення спільного множника за дужки:
1) (a – 1) (a + 2) – (a – 2) (a + 2) + (a – 3) (a + 2) – (a – 4) (a + 2);
2) (3a 2) (5b2 4b 10) (2 3a) (5b2 6b 10); 3) (4a 7b) (2a 2 4ab b2) (4a 7b) (2a 2 4ab b2).
¿ 508.•• Спростіть вираз, використовуючи винесення спільного множника за дужки:
1) ab (a 2 ab b2) ab (a 2 ab b2);
2) (a + b) (a + 1) – (a + b) (1 – b) + (b + a) (b – a).
509.•• Розв’яжіть рівняння 4x 2 1,2x a, якщо один із його коренів дорівнює 0,3.
510.•• Розв’яжіть рівняння 5x 2 8x a, якщо один із його коренів дорівнює –1,6.
511.•• Винесіть за дужки спільний множник (n — натуральне число):
1) an +1 + an; 4) d 2n −dn;
2) bn −bn −3, n > 3; 5) 2n 3 3æ2n 2 5æ2n 1; 3) cn 2 cn 4, n > 4; 6) 9n +1 +3n + 2.
512.•• Розкладіть на множники (n — натуральне число):
1) an 2 an; 2) 3bn 2 2bn 1 bn; 3) 32n +162n +1.
513.•• Відомо, що при деякому значенні y значення виразу y2 – 4y + 2 дорівнює 6. Знайдіть при цьому значенні y значення виразу:
1) 5y 2 20y 10; 3) 3y 2 12y 8.
2) y 2 (y 2 4y 2) 4y (y 2 4y 2);
514.•• Відомо, що при деякому значенні a значення виразу a2 + 2a – 5 дорівнює –4. Знайдіть при цьому значенні a значення виразу:
1) 2a 2 4a 10;
2) a 2 (a 2 2a 5) 2a (a 2 2a 5);
3) 4a 2 8a 16.
515.•• При якому значенні a не має коренів рівняння:
1) (x + 1) (x – 3) – x (x – 3) = ax; 2) x (5x – 1) – (x – a) (5x – 1) = 4x – 2a; 3) (2x – 5) (x + a) – (2x + 3) (x + 1) = 4?
516.•• При якому значенні a має безліч коренів рівняння:
1) (x – 4) (x + a) – (x + 2) (x – a) = –6; 2) x (3x – 2) – (x + 2a) (3x + 2) = 5a + 6?
¿ 517.* Знайдіть усі двоцифрові числа, які дорівнюють добутку їхніх цифр, збільшених на 1.
![]()
518. Спростіть вираз:
2
1) 0,42ac3æ1![]() a 4c2; 3) 2
a 4c2; 3) 2![]() m 2np3æ
m 2np3æ ![]() np4 ;
np4 ;
5
2) 1,2xyzæ2![]() x 5y 6; 4) 1
x 5y 6; 4) 1![]() x 2y 3 æ
x 2y 3 æ![]() x 8y 2.
x 8y 2.
519. За тиждень в офісі витрачають 1400 аркушів паперу. Яку найменшу кількість пачок паперу потрібно купити, щоб забезпечити роботу офісу протягом 6 тижнів, якщо в одній пачці міститься 500 аркушів?
520. Вміст солі в морській воді становить 5 %. Скільки кілограмів прісної води треба додати до 30 кг морської води, щоби вміст солі в утвореному розчині становив 3 %?
521. Для ремонту школи придбали фарбу. Першого дня витратили на 2 банки фарби більше за половину всієї фарби, а другого — ![]() кількості банок фарби, витраченої за перший день. Після
кількості банок фарби, витраченої за перший день. Після
цього залишилося 2 банки. Скільки банок фарби було придбано?
522. У коробці лежать 2 червоних, 4 зелених і 10 синіх олівців.
Яка ймовірність того, що навмання взятий олівець буде:
1) червоним; 2) зеленим; 3) не зеленим?
Яку найменшу кількість олівців треба взяти навмання, щоб серед них обов’язково був синій олівець?
¿ 523. Чи існує двоцифрове число, у якому цифра десятків на 4 більша за цифру одиниць, а різниця між даним числом і числом, записаним тими самими цифрами, але у зворотному порядку, дорівнює 27?
 УЧИМОСЯ РОБИТИ НЕСТАНДАРТНІ КРОКИ
УЧИМОСЯ РОБИТИ НЕСТАНДАРТНІ КРОКИ
524. З аркуша картону вирізали кілька рівних рівносторонніх трикутників. У вершинах кожного написали цифри 1, 2, 3. Потім ці трикутники склали в стіс. Чи могло статися так, що сума чисел уздовж кожного ребра стосу дорівнює 55?
![]() 13. Розкладання многочлена на множники.
13. Розкладання многочлена на множники.
Метод групування
Многочлен ax +bx + ay +by не вдасться розкласти на множники методом винесення за дужки спільного множника, оскільки множника, спільного для всіх доданків, немає. Проте члени цього многочлена можна об’єднати в групи так, що доданки кожної групи матимуть спільний множник: ax bx ay by (ax bx) (ay by) x (a b) y (a b).
Ми отримали вираз, у якому обидва доданки мають множник (a + b). Винесемо його за дужки:
x (a b) y (a b) (a b) (x y).
Заданий многочлен удалося розкласти на множники завдяки тому, що ми в зручний спосіб об’єднали його члени в групи. Тому описаний прийом розкладання многочлена на множники називають методом групування.
![]() ПРИКЛАД 1 Розкладіть на множники многочлен:
ПРИКЛАД 1 Розкладіть на множники многочлен:
1) 2ac + 2bc + 5am + 5bm; 3) xy – 12 + 4x – 3y. 2) x4 – 2x3 – 3x + 6;
Розв’язання. 1) Згрупувавши члени даного многочлена так, щоб доданки в кожній групі мали спільний множник, отримуємо: 2ac + 2bc + 5am + 5bm = (2ac + 2bc) + (5am + 5bm) = = 2c (a + b) + 5m (a + b) = (a + b) (2c + 5m).
Той самий результат можна отримати, якщо доданки згрупувати в інший спосіб:
(2ac + 5am) + (2bc + 5bm) = a (2c + 5m) + b (2c + 5m) = = (2c + 5m) (a + b).
2) Маємо: x4 – 2x3 – 3x + 6 = (x4 – 2x3) – (3x – 6) = = x3 (x – 2) – 3 (x – 2) = (x – 2) (x3 – 3).
3) xy – 12 + 4x – 3y = (xy + 4x) + (–12 – 3y) = x (y + 4) – 3 (4 + y) =
![]() = (y + 4) (x – 3).
= (y + 4) (x – 3). ¤
![]() ПРИКЛАД 2 Розкладіть на множники тричлен x2 + 6x + 8.
ПРИКЛАД 2 Розкладіть на множники тричлен x2 + 6x + 8.
Розв’язання. Подавши доданок 6x у вигляді суми 2x + 4x, застосуємо метод групування:
x2 + 6x + 8 = x2 + 2x + 4x + 8 = (x2 + 2x) + (4x + 8) =  = x (x + 2) + 4 (x + 2) = (x + 2) (x + 4).
= x (x + 2) + 4 (x + 2) = (x + 2) (x + 4).
525.° Закінчіть розкладання многочлена на множники:
1) 3m + 3n + mx + nx = (3m + 3n) + (mx + nx) = 3 (m + n) + + x (m + n) = ...;
2) 8c – 8 – ac + a = (8c – 8) + (–ac + a) = 8 (c – 1) – a (...;
3) 4ab + 8b + 3a + 6 = (4ab + 8b) + (3a + 6) = 4b (a + 2) + ...;
4) a2b + 2c2 – abc – 2ac = a2b – abc + 2c2 – 2ac = (a2b – abc) + + (2c2 – 2ac) = ab (a – c) + 2c (c – a) = ... .
526.° Закінчіть розкладання многочлена на множники:
1) 5a + 5c – ab – bc = (5a + 5c) + (– ab – bc) =
= 5 (a + c) – b (a + c) = ...;
2) xy + 2y – x – 2 = (xy + 2y) + (– x – 2) = y (x + y) – ...; 3) x3 + x2 + x + 1 = (x3 + x2) + (x + 1) = ... .
527.° Подайте у вигляді добутку многочленів вираз:
1) a (b + c) + 4b + 4c; 3) m (n – 2) + n – 2; 2) x (y – 8) + 6y – 48; 4) x (m – n) + n – m.
528.° Розкладіть на множники:
1) b (p – k) + cp – ck; 3) a (c – 6) + 5c – 30; 2) a (b + 9) + b + 9; 4) 7 – x + y (x – 7). 529.° Розкладіть на множники многочлен:
1) ma + mb + 4a + 4b; 5) a – 1 + ab – b;
2) 3x + cy + cx + 3y; 6) xy + 8y – 2x – 16;
3) 5a – 5b + ap – bp; 7) ab + ac – b – c; 4) 7m + mn + 7 + n; 8) 3p – 3k – 4ap + 4ak.
530.° Подайте у вигляді добутку многочленів вираз:
1) ay – 3y – 4a + 12; 4) 8x – 8y + xz – yz;
2) 9a + 9 – na – n; 5) mn + m – n – 1; 3) 6x + ay + 6y + ax; 6) ab – ac – 2b + 2c.
531.• Розкладіть на множники многочлен:
|
1) a3 + a2 + a + 1; |
5) a2 ab ac bc; |
|
|
2) x 5 3x 3 4x 2 12; |
6) 20a3bc 28ac2 15a 2b2 |
21bc; |
|
3) c6 – 10c4 – 5c2 + 50; |
7) x2y2 + xy + axy + a; |
|
|
4) y 3 18 6y 2 3y; |
8) 24x 6 44x 4y 18x 2y 3 |
33y 4. |
532.• Розкладіть на множники многочлен:
1) 8c3 2c2 4c 1; 4) 8a 2 2ab 4ac bc;
2) x 2y + x + xy 2 + y; 5) 2b3 7b2c 4b 14c;
3) 9a2b – 3a2 + 3b2 – b; 6) 6x 5 4x 2y 2 9x 3y 6y 3.
533.• Знайдіть значення виразу, розклавши його попередньо на множники:
1) 2a 3 3a 2 2ab 3b, якщо a = 0,5, b = 2,25; 2) xy y 2 12x 12y, якщо x = 10,8, y = –8,8; 3) 27x 3 36x 2 6x 8, якщо x 1![]() .
.
534.• Знайдіть значення виразу: 1) 2a +b+2a 2 + ab, якщо a = –3, b = 4;
2) 3x 3 x 2 6x 2, якщо x = ![]() .
.
535.• Закінчіть обчислення значення виразу:
1) 38 14 12 26, æ , 12 26 11 86, æ , 24 37, æ2 26, 2 26 25 63, æ ,
()38 14 12 26, æ , 12 26 11 86, æ , ) ( 24 37, æ2 26, 2 26 25 63, æ ,
12 26, æ(38 14, 11 86, ) 2 26, æ(24 37, 25 63, ) ...;
2) 0 7, æ2 48, 0 3 1 62, æ , 0 4 2 48, æ , 0 3 3 14, æ ,
(....0 7, æ2 48, 0 4 2 48, æ , ) (0 3 3 14, æ , 0 3 1 62, æ , )
536.• Обчисліть, не використовуючи калькулятора:
1) 3,742 3,74æ2,26 3,74æ1,24 2,26æ1,24; 2) 58,7æ1,2 36æ3,52 34,7æ1,2 2,32æ36; 3) 2![]() æ3
æ3![]() +1
+1![]() æ2,8 +2
æ2,8 +2![]() æ3
æ3![]() +1
+1![]() æ2,2.
æ2,2.
537.• Знайдіть значення виразу:
1) 34,4æ13,7 34,4æ8,7 15,6æ8,7 13,7æ15,6; 2) 0,63 2æ0,62æ0,8 0,6æ0,82 2æ0,83.
538.• Розкладіть на множники многочлен:
1) ax 2 ay bx 2 by cx 2 cy;
2) a 2b+ a + ab2 +b+3ab+3;
3) x3 – x2 + x2y + x – xy + y;
4) m 2n mn 5 5m n 5m 2;
5) x 6 2x 5 4x 3 8x 2 5x 10;
6) a 3b ab2 abc3 a2c bc c4.
539.• Подайте вираз у вигляді добутку многочленів:
1) ab + ac + ad + bx + cx + dx;
2) 7p – 7k – px + kx + k – p;
3) x 3y 3 x 2y 2 xy 6 6xy 6x 2y 2; 4) a5 a 4b a 3b2 a 2b3 ab4 b5.
540.•• Розкладіть на множники вираз (n — натуральне число):
1) an +1 + an + a +1;
2) bn 2 b 1 bn 1;
3) 3yn + 3 – 3y2 – 5 + 5yn + 1.
541.•• Розкладіть на множники тричлен, подавши попередньо один із його членів у вигляді суми подібних доданків:
1) x 2 +8x +12; 2) x 2 5x 4; 3) x 2 7x 8; 4) x 2 −4x −5.
542.•• Розкладіть на множники тричлен:
1) x 2 +4x +3; 2) x 2 10x 16; 3) x 2 3x 18; 4) x 2 −4x −32.
543.* Доведіть, що при всіх натуральних значеннях n значення виразу n 3 +3n 2 +2n ділиться націло на 6.
544.* Розкладіть на множники многочлен a 2 +b2 + c2 +2ab+2bc +2ac.
545.* Доведіть, що при будь-якому натуральному значенні n, яке більше за 1, значення виразу 3n 2 2n 2 3n 2n ділиться націло на 10.
546.* Відомо, що при деяких значеннях x і y виконується рівність x2 + y2 = 1. Знайдіть при цих самих значеннях x і y значення виразу 2x 4 +3x 2y 2 + y 4 + y 2.
![]()
547. Ціну на деякий товар спочатку знизили на 20 %, а потім підвищили на 20 %. Як змінилася ціна цього товару порівняно з початковою (підвищилася чи знизилася) і на скільки відсотків?
548. Ціну на деякий товар спочатку підвищили на 10 %, а потім знизили на 30 %. Як змінилася ціна цього товару порівняно з початковою (підвищилася чи знизилася) і на скільки відсотків?
549. (Задача з українського фольклору.) Підпасок привів на полонину овець. На полонині були кілки. Якщо до кожного кілка він прив’яже по вівці, то для однієї кілка не вистачить. Якщо ж до кожного кілка він прив’яже по дві вівці, то один кілок залишиться вільним. Скільки овець привів підпасок?
¿ 550. Ольга й Дмитро можуть прополоти город, працюючи разом, за 2,4 год. Ольга може зробити це самостійно за 4 год. Скільки часу потрібно Дмитру, щоб самостійно прополоти город?
551. В одному бідоні було в 4 рази більше молока, ніж у другому. Коли з першого бідона перелили 10 л молока в другий, то об’єм молока в другому бідоні склав ![]() об’єму молока, що залишилося в першому бідоні. Скільки літрів молока було в кожному бідоні спочатку?
об’єму молока, що залишилося в першому бідоні. Скільки літрів молока було в кожному бідоні спочатку?
![]() ГОТУЄМОСЯ ДО ВИВЧЕННЯ НОВОЇ ТЕМИ
ГОТУЄМОСЯ ДО ВИВЧЕННЯ НОВОЇ ТЕМИ
552. Піднесіть до квадрата одночлен:
1) 2a; 3) 3b3; 5) 0,3x; 7) ![]() a 2b3c4;
a 2b3c4;
2) a 2; 4) 7x 4; 6) 0,4y 5z 2; 8) 1![]() m 6n.
m 6n.
¿ 553. Запишіть у вигляді виразу:
1) суму чисел a і c;
2) різницю чисел m і n;
3) добуток суми чисел x і y та їхньої різниці;
4) квадрат різниці чисел x і y; 5) різницю квадратів чисел x і y.
 УЧИМОСЯ РОБИТИ НЕСТАНДАРТНІ КРОКИ
УЧИМОСЯ РОБИТИ НЕСТАНДАРТНІ КРОКИ
554. У турнірі, організованому за олімпійською системою (той, хто програв, — вибуває), беруть участь n тенісистів. Яку кількість матчів треба провести, щоб виявити переможця турніру?
ЗАВДАННЯ № 3 «ПЕРЕВІРТЕ СЕБЕ» В ТЕСТОВІЙ ФОРМІ
1. Подайте у вигляді многочлена вираз 3y2 (y3 + 1).
А) 3y6 + 1; В) 3y5 + 1; Б) 3y6 + 3y2; Г) 3y5 + 3y2.
2. Спростіть вираз –9y (y – 3) + 4,5y (2y – 4).
А) 45y; В) –9y;
Б) –45y; Г) 9y.
3. Якому многочлену дорівнює вираз (x – 3) (x + 7)?
А) x2 + 4x – 21; В) x2 + 10x – 21;
Б) x2 – 4x – 21; Г) x2 – 10x – 21.
4. Спростіть вираз (3x + 2) (2x – 1) – (5x – 2) (x – 4).
А) x2 – 23x – 10; В) x2 – 21x + 6; Б) x2 + 23x – 10; Г) x2 + 21x + 6.
5. Винесіть спільний множник за дужки: 3mn – 4mk.
А) n (3m – 4k); В) n (4m – 3k); Б) m (3n – 4k); Г) m (4n – 3k).
6. Розкладіть на множники вираз m2n + mn2.
А) m (m + n); В) mn (m + n); Б) n (m + n); Г) m2n2 (m + n).
7. Розкладіть вираз mn – mn2 на множники.
А) mn (1 – n); В) m (1 – n) (1 – n); Б) mn (1 + n); Г) n (1 – m) (1 – m).
8. Подайте многочлен 2x2 – 4x6 у вигляді добутку одночлена та многочлена.
А) 2x2 (1 – 2x3); В) 2x2 (2 – x3); Б) 2x2 (1 – 2x4); Г) 2x2 (2 – x4).
9. Розв’яжіть рівняння x2 – 2x = 0.
А) 0; В) 0; 2;
Б) 0; –2; Г) 2.
10. Подайте у вигляді добутку многочлен ax – ay + 5x – 5y. А) (x – y) (a + 5); В) (x + y) (a – 5); Б) (x – y) (a – 5); Г) (x + y) (a + 5).
11. Розв’яжіть рівняння x 1 x 1 1.
2 3
А) 11; В) 7; Б) 1; Г) 5.
12. Значення змінної a є таким, що значення виразу a2 – 7a + 3 дорівнює 2. Знайдіть значення виразу 2a2 – 14a + 10.
А) 4; В) 8;
Б) 12; Г) 14.
![]() 14. Добуток різниці та суми двох виразів
14. Добуток різниці та суми двох виразів
Нерідко в математиці, крім знання загального закону (теореми), зручно користуватися правилами, що застосовуються в окремих (особливих) випадках.
Наприклад, коли множать десятковий дріб на 10, 100, 1000 й т. д., то немає потреби використовувати загальний алгоритм множення у стовпчик, а набагато зручніше застосувати правило перенесення коми.
Особливі ситуації трапляються також при множенні многочленів.
Розглянемо окремий випадок, коли в добутку двох многочленів один із них є різницею двох виразів, а другий — їхньою сумою.
Маємо:
(a b) (a b) a2 ab ba b2 a 2 b2.
Отримали тотожність
|
(a |
b) (a |
b) |
a 2 |
b2 |
Тепер при множенні різниці виразів на їхню суму можна скоротити роботу, одразу записавши результат — різницю квадратів цих виразів. Тому цю тотожність називають формулою скороченого множення. Її виражає таке правило:
добуток різниці двох виразів та їхньої суми дорівнює різниці
квадратів цих виразів.
![]() ПРИКЛАД 1 Виконайте множення многочленів:
ПРИКЛАД 1 Виконайте множення многочленів:
1) (2a – 5b) (2a + 5b);
2) (y2 + 3x4) (3x4 – y2);
3) (–4mn – p) (4mn – p).
Розв’язання. 1) (2a – 5b) (2a + 5b) = (2a)2 – (5b)2 = 4a2 – 25b2.
2) (y2 + 3x4) (3x4 – y2) = (3x4 + y2) (3x4 – y2) = (3x4)2 – (y2)2 = 9x8 – y4.
3) (–4mn – p) (4mn – p) = (–p – 4mn) (–p + 4mn) =
![]() = (–p)2 – (4mn)2 = p2 – 16m2n2. ¤
= (–p)2 – (4mn)2 = p2 – 16m2n2. ¤
![]() ПРИКЛАД 2 Спростіть вираз:
ПРИКЛАД 2 Спростіть вираз:
1) (b – 3) (b + 3) – (2b + 1) (2b – 1);
2) –2x (x + 5) (5 – x);
3) (a3 – 2) (a3 + 2) (a6 + 4).
Розв’язання. 1) (b – 3) (b + 3) – (2b + 1) (2b – 1) =
= b2 – 9 – (4b2 – 1) = b2 – 9 – 4b2 + 1 = –3b2 – 8.
2) –2x (x + 5) (5 – x) = –2x (25 – x2) = –50x + 2x3.
3) Застосувавши двічі формулу добутку різниці та суми двох виразів, отримаємо:

1) (b – c) (b + c) = b2 – c2; 3) (x + y) (y – x) = y2 – x2; 2) (m + n) (m – n) = m2 + n2; 4) (p – q) (p + q) = (p – q)2?
556.° Якому з наведених многочленів тотожно дорівнює добуток (7a 2b) (7a 2b):
1) 7a 2 −2b2; 2) 7a 2 +2b2; 3) 49a2 −4b2; 4) 49a 2 +4b2 ?
557.° Закінчіть перетворення виразу в многочлен:
1) (c – 8) (c + 8) = c2 – 82 = ...;
2) (5x – 7y2) (5x + 7y2) = (5x)2 – (7y2)2 = ...;
3) (a4 + b3) (b3 – a4) = (b3 + a4) (b3 – a4) = (b3)2 – (a4)2 = ...; 4) (–9xy – z) (9xy – z) = –(9xy + z) (9xy – z) = –((9xy)2 – z2) = ... .
558.° Закінчіть перетворення виразу в многочлен:
1) (2ab + 3) (2ab – 3) = (2ab)2 – 32 = ...;
2) (6m2 – 11p5) (11p5 + 6m2) = (6m2 – 11p5) (6m2 + 11p5) = = (6m2)2 – ... .
559.° Виконайте множення многочленів:
1) (m – n) (m + n); 6) (4a – b) (b + 4a); 2) (x – 1) (x + 1); 7) (5b + 1) (1 – 5b);
3) (9 – y) (9 + y); 8) (3x – 5y) (3x + 5y); 4) (3b – 1) (3b + 1); 9) (13c – 10d) (13c + 10d); 5) (10m – 7) (10m + 7); 10) (8m + 11n) (11n – 8m).
560.° Подайте у вигляді многочлена вираз:
|
1) (c – 2) (c + 2); |
5) (x + 7) (7 – x); |
|
2) (12 – x) (12 + x); |
6) (5a – 8b) (5a + 8b); |
|
3) (3x + y) (3x – y); |
7) (8m + 2) (2 – 8m); |
|
4) (6x – 9) (6x + 9); |
8) (13c – 14d) (14d + 13c). |
561.° Виконайте множення:
|
1) (a 2 |
3) (a 2 |
3); |
6) (11a 3 5b2) (5b2 |
11a 3); |
|
2) (5 |
b2) (b2 |
5); |
7) (7 xy) (7 xy); |
|
3) (3x 2y 2) (3x 2y 2); 8) 8a 3b ![]() ab2 8a 3b
ab2 8a 3b ![]() ab2 ;
ab2 ;
4) (10p3 7k) (10p3 7k); 9) (0,3m 5 0,1n 3) (0,3m 5 0,1n 3); 5) (4x 2 8y 3) (4x 2 8y 3); 10) ![]() a 2c 1,4b4 1,4b4
a 2c 1,4b4 1,4b4 ![]() a 2c .
a 2c .
|
562.° Виконайте множення: |
|
|
|
1) (x 3 4) (x 3 4); |
5) (6a 3 8b) (6a 3 8b); |
|
|
2) (ab c) (ab c); |
6) (5n 4 m 4) (5n 4 m 4); |
|
|
3) (x y 2) (y 2 x); |
7) (0,2m 8 0,8n 6) (0,2m 8 |
0,8n 6); |
![]()
![]() 4) (3m 2 2c) (3m 2 2c); 8) p7k 9 4 k 9 2 p7 .
4) (3m 2 2c) (3m 2 2c); 8) p7k 9 4 k 9 2 p7 .
11 7
563.° Спростіть вираз:
1) (2a b) (2a b) b2;
2) 10x 2 (y 5x) (y 5x);
3) 64m 2 (8m 9) (8m 9);
4) (4x – 7y) (4x + 7y) + (7x – 4y) (7x + 4y); 5) (a – 2) (a + 3) + (6 – a) (a + 6); 6) 3a (a – b) – (3a + 2b) (3a – 2b).
564.° Спростіть вираз:
1) (9a 2) (9a 2) 18a 2; 3) (b + 7) (b – 4) + (2b – 6) (2b + 6);
2) 25m 2 (5m 7) (5m 7); 4) 4x (3x – 10y) – (4x + y) (4x – y).
565.• На який вираз треба помножити двочлен 0,3x3 – xy2, щоб їхній добуток дорівнював двочлену 0,09x6 – x2y4?
566.• На який вираз треба помножити многочлен 7t4 + 9p5, щоб їхній добуток дорівнював многочлену 49t8 – 81p10?
567.• Які одночлени треба поставити замість зірочок, щоб виконувалася тотожність:
1) (* 12a) (* *) 9b2 *; 3) (0,7 p *) (* 0,7 p) ![]() m 8 0,49p2;
m 8 0,49p2;
2) (* 5c) (* 5c) 16d 2 *; 4) (3m 2 *) (* *) 9m 4 n 6 ?
568.• Поставте замість зірочок такі одночлени, щоб виконувалася тотожність:
1) (8a 2b *) (8a 2b *) * 25c6;
2) ![]() * 1 x 4y 5 1 a 2 * 1 a 4x 8y 10.
* 1 x 4y 5 1 a 2 * 1 a 4x 8y 10.
12 15 225
569.• Подайте у вигляді многочлена вираз:
1) a (a – 2) (a + 2); 4) (c d) (c d) (c2 d 2);
2) –3 (x + 3) (x – 3); 5) (2a 1) (2a 1) (4a 2 1); 3) 7b2 (b 4) (4 b); 6) (c3 5) (c3 5) (c6 25).
570.• Виконайте множення:
1) 5b (b – 1) (b + 1); 3) (m 10) (m 2 100) (m 10); 2) (c 2) (c 2)æ8c2; 4) (a 2 1) (a 2 1) (a 4 1).
571.• Виконайте множення двочленів (n — натуральне число):
1) (an 4) (an 4); 3) (x 4n yn 2) (yn 2 x 4n); 2) (b2n c3n) (b2n c3n); 4) (an 1 bn 1) (an 1 bn 1), n > 1.
572.• Спростіть вираз:
1) (8a – 3) (8a + 3) – (7a + 4) (8a – 4);
2) 0,6m (2m – 1) (2m + 1) + 0,3 (6 + 5m) (6 – 5m); 3) (7 – 2x) (7 + 2x) – (x – 8) (x + 8) – (4 – 3x) (5 + 3x); 4) b2c (4b c2) (4b c2) 16b4c.
573.• Спростіть вираз:
1) (x + 1) (x – 1) – (x + 5) (x – 5) + (x + 1) (x – 5); 2) 81a 8 (3a2 b3) (9a 4 b6) (3a 2 b3).
574.• Розв’яжіть рівняння:
1) 8x (3 + 2x) – (4x + 3) (4x – 3) = 9x – 6;
2) 7x – 4x (x – 5) = (8 – 2x) (8 + 2x) + 27x; 3) (6x + 7) (6x – 7) + 12x = 12x (3x + 1) – 49;
4) (x 2) (x 2) (x 2 4) (x 4 16) x 8 10x.
575.• Розв’яжіть рівняння:
1) (x 17) (x 17) x 2 6x 49;
2) (1,2x – 4) (1,2x + 4) – (1,3x – 2) (1,3x + 2) = 0,5x (8 – 0,5x).
576.• Доведіть, що значення виразу не залежить від значення змінної (змінних):
1) (x – 9) (x + 9) – (x + 19) (x – 19);
2) (2a – b) (2a + b) + (b – c) (b + c) + (c – 2a) (c + 2a).
¿ 577.• Доведіть, що при будь-якому натуральному n значення виразу (7n + 8) (7n – 8) – (5n + 10) (5n – 10) ділиться націло на 12.
578.• Доведіть, що не існує такого натурального числа n, при якому значення виразу (4n + 3) (9n – 4) – (6n – 5) (6n + 5) – 3 (n – 2) ділиться націло на 8.
579.• Доведіть, що при будь-якому натуральному n значення виразу (9n – 4) (9n + 4) – (8n – 2) (4n + 3) + 5 (6n + 9) ділиться націло на 7.
580.•• Знайдіть значення виразу:
1) 320æ620 (1810 2) (1810 2);
2) (5 2817 ) (5 2817 ) 1434æ234;
3) 7 36æ812 (1418 3) (1418 3);
4) (32 1) (32 1) (34 1) (38 1) (316 1) (332 1) 364;
5) (2 + 1) (22 + 1) (24 + 1) (28 + 1) (216 + 1) – 232.
581.•• Чому дорівнює значення виразу: 1) 8115æ820 (630 1) (630 1);
2) 524 (53 2) (53 2) (56 4) (512 16)?
582.* Порівняйте значення виразів, не обчислюючи їх:
1) 415æ425 і 426æ414; 2) 1 234 567æ1 234 569 і 1 234 5682.
583.* Порівняйте значення виразів, не обчислюючи їх:
1) 253æ259 і 252æ260; 2) 987 6542 і 987 646æ987 662.
![]()
584. Олеся й Остап купили однакові ручки. Ціна кожної з них дорівнює цілому числу гривень. Олеся заплатила за ручки 65 грн, а Остап — на 39 грн більше. Скільки коштує одна ручка? Скільки ручок купив Остап?
585. Від села до станції Василько може доїхати на велосипеді за 3 год, а дійти пішки — за 7 год. Швидкість руху пішки на 8 км/год менша від швидкості руху на велосипеді. З якою швидкістю їздить Василько на велосипеді? Яка відстань від села до станції?
586. В одному мішку було 60 кг цукру, а в другому — 100 кг. Коли з другого мішка взяли в 4 рази більше цукру, ніж із першого, то в першому залишилось у 2 рази більше цукру, ніж у другому. Скільки кілограмів цукру взяли з кожного мішка?
587. Один вантажний автомобіль може перевезти зібраний з поля врожай за 10 год, другий — за 12 год, а третій — за 15 год. За скільки годин вони зможуть перевезти врожай, працюючи разом?
588. (Старовинна єгипетська задача.) Кожний із 7 чоловіків має
7 кішок. Кожна кішка з’їдає по 7 мишей, кожна миша за одне літо може знищити 7 ячмінних колосків, а із зерен одного колоска може вирости 7 жмень ячмінного зерна. Маса однієї жмені зерна — 80 г. Скільки жмень зерна щорічно рятують кішки?
Скільки це становить тонн зерна? Відповідь округліть до сотих.
589. Розв’яжіть рівняння:
1) ![]() x 1; 2) 3x 2 2x 1 5 x .
x 1; 2) 3x 2 2x 1 5 x .
9 6 3
![]() ГОТУЄМОСЯ ДО ВИВЧЕННЯ НОВОЇ ТЕМИ
ГОТУЄМОСЯ ДО ВИВЧЕННЯ НОВОЇ ТЕМИ
590. Подайте даний вираз у вигляді квадрата одночлена:
1) x 6; 3) 4x 2; 5) a 8b10; 7) 1,21m10n 20; 2) y 4; 4) ![]() x 4; 6) 0,36x 2y 12; 8) 1
x 4; 6) 0,36x 2y 12; 8) 1![]() a14b16.
a14b16.
591. Чи можна подати у вигляді різниці квадратів двох одночленів вираз:
1) a 2 −16b2; 3) 100b4 −25c6; 5) −a12 −49c8;
2) 25c2 + 9b2; 4) 64 a10; 6) –0,01a4 + 0,04b4?
У разі ствердної відповіді запишіть цю різницю квадратів.
 УЧИМОСЯ РОБИТИ НЕСТАНДАРТНІ КРОКИ
УЧИМОСЯ РОБИТИ НЕСТАНДАРТНІ КРОКИ
592. Для перевезення вантажу виділено 4-, 7- і 8-тонні вантажівки. Кожний автомобіль має зробити тільки один рейс. Скільки треба вантажівок кожного виду для перевезення 44 т вантажу?
![]() 15. Різниця квадратів двох виразів
15. Різниця квадратів двох виразів
Ви вже знаєте два способи розкладання многочленів на множники: винесення спільного множника за дужки та метод групування.
Розглянемо ще один спосіб.
Формулу (a – b) (a + b) = a2 – b2 перепишемо так:
a 2 b2 (a b) (a b)
Цю тотожність називають формулою різниці квадратів двох виразів.
Тепер можна сформулювати правило.
Різниця квадратів двох виразів дорівнює добутку різниці цих виразів та їхньої суми.
Наведемо приклади застосування цієї формули для розкладання многочленів на множники.
![]() ПРИКЛАД 1 Розкладіть на множники:
ПРИКЛАД 1 Розкладіть на множники:
1) a2 – 4; 2) 36m 2 −2 7 n 8; 3) –a2b6 + 1.
9
Розв’язання. 1) Маємо: a2 – 4 = a2 – 22 = (a – 2) (a + 2).
2
2) 36m 2 2![]() n 8 36m 2
n 8 36m 2 ![]() n 8 (6m)2
n 8 (6m)2 ![]() n 4
n 4
6m ![]() n 4 6m
n 4 6m ![]() n 4 .
n 4 .
3) ![]() –a2b6 + 1 = 1 – a2b6 = (1 – ab3) (1 + ab3). ¤
–a2b6 + 1 = 1 – a2b6 = (1 – ab3) (1 + ab3). ¤
![]() ПРИКЛАД 2 Розкладіть на множники, використовуючи формулу різниці квадратів:
ПРИКЛАД 2 Розкладіть на множники, використовуючи формулу різниці квадратів:
1) 100 – (a + 5)2; 2) (2a + 3b)2 – (3a – b)2.
Розв’язання. 1) 100 – (a + 5)2 = 102 – (a + 5)2 =
= (10 – (a + 5)) (10 + (a + 5)) =
= (10 – a – 5) (10 + a + 5) = (5 – a) (15 + a).
2) ![]() (2a + 3b)2 – (3a – b)2 = ((2a + 3b) – (3a – b)) ((2a + 3b) + + (3a – b)) = (2a + 3b – 3a + b) (2a + 3b + 3a – b) = (4b – a) (5a + 2b). ¤
(2a + 3b)2 – (3a – b)2 = ((2a + 3b) – (3a – b)) ((2a + 3b) + + (3a – b)) = (2a + 3b – 3a + b) (2a + 3b + 3a – b) = (4b – a) (5a + 2b). ¤
![]() ПРИКЛАД 3 Розв’яжіть рівняння:
ПРИКЛАД 3 Розв’яжіть рівняння:
1) x2 – 36 = 0; 2) (2x – 7)2 – 81 = 0.
Розв’язання. 1) Застосувавши формулу різниці квадратів та умову рівності добутку нулю, отримуємо: (x – 6) (x + 6) = 0; x – 6 = 0 або x + 6 = 0; x = 6 або x = –6. Відповідь: 6; –6.
2) Маємо:
(2x – 7 – 9) (2x – 7 + 9) = 0;
(2x – 16) (2x + 2) = 0;
![]() 2x – 16 = 0 або 2x + 2 = 0; x = 8 або x = –1. Відповідь: 8; –1. ¤
2x – 16 = 0 або 2x + 2 = 0; x = 8 або x = –1. Відповідь: 8; –1. ¤
![]() ПРИКЛАД 4 Доведіть, що при будь-якому натуральному n значення виразу (6n + 7)2 – (2n – 1)2 ділиться націло на 8.
ПРИКЛАД 4 Доведіть, що при будь-якому натуральному n значення виразу (6n + 7)2 – (2n – 1)2 ділиться націло на 8.
Розв’язання. Маємо:
(6n + 7)2 – (2n – 1)2 = (6n + 7 – 2n + 1) (6n + 7 + 2n – 1) = = (4n + 8) (8n + 6) = 4 (n + 2)æ2 (4n + 3) = 8 (n + 2) (4n + 3).
![]() Даний вираз подано у вигляді добутку трьох множників, один з яких дорівнює 8, а два інших — теж натуральні числа. Звідси випливає, що значення даного виразу ділиться націло на 8 при будь-якому натуральному n. ¤
Даний вираз подано у вигляді добутку трьох множників, один з яких дорівнює 8, а два інших — теж натуральні числа. Звідси випливає, що значення даного виразу ділиться націло на 8 при будь-якому натуральному n. ¤

593.° Яким із наведених добутків многочленів тотожно дорівнює многочлен a 2 −144:
1) (a −12)2; 3) (12 – a) (12 + a);
2) (a – 12) (a + 12); 4) (12 – a) (–12 – a)?
594.° Яка з даних рівностей є тотожністю:
1) 49 b2 (7 b) (7 b); 3) 49 b2 (7 b)2; 2) 49 b2 (b 7) (b 7); 4) 49 b2 (b 49) (b 49)?
¿ 595.° Чи можна, застосовуючи формулу різниці квадратів, розкласти на множники вираз:
1) a 2 −9; 4) 25 + x 2; 7) 81 +100p2; 10) −m 2n 2 −25?
2) b2 +1; 5) 1 − y 2; 8) 81 −100p2;
3) 4 −c2; 6) 16a 2 −b2; 9) m 2n 2 −25;
Якщо це можливо, то виконайте розкладання на множники. 596.° Розкладіть на множники:
1) b2 −d 2; 7) 900 −81k 2; 13) a 2b2c2 −1;
2) x 2 −1; 8) 16x 2 −121y 2; 14) 100a 2 −0,01b2;
3) x 2 1; 9) b2c2 −1; 15) a 4 −b2;
4) 36 −c2; 10) 1 x 2 − 1 y 2; 16) p2t 2 −0,36k 2d 2;
4 9
5) 4 −25a 2; 11) 4a 2b2 25; 17) y 10 −9;
6) 49a 2 −100; 12) 144x 2y 2 −400; 18) 4x 12 −111 y 16.
25
597.° Розкладіть на множники:
1) 16 −b2; 5) 4x 2 −25; 9) 4a2c2 −9x 2y 2;
2) c2 −49; 6) 81c2 −64d 2; 10) x 24 − y 22;
3) 0,04 −a 2; 7) 0,09x 2 −0,25y 2; 11) 1600 a12;
4) x 2 − 4; 8) a 2b4 −c6d 8; 12) a18 − 49.
9 64
598.° Обчисліть, застосовуючи формулу різниці квадратів: 1) 862 – 762; 3) 7,322 – 6,322; 5) 8,542 – 1,462;
![]() 2) 1072 – 932; 4) 19,42 – 19,32; 6) 3 2 2 22 .
2) 1072 – 932; 4) 19,42 – 19,32; 6) 3 2 2 22 .
3
599.° Знайдіть значення виразу x2 – y2, якщо: 1) x = 75, y = 25; 3) x = 5,89, y = 4,11; 2) x = 10,5, y = 9,5; 4) x = 3,04, y = 1,96.
600.° Розв’яжіть рівняння:
1) x2 – 49 = 0; 3) x2 + 36 = 0; 5) 9x2 – 4 = 0;
2) ![]() z 2 0; 4) x2 – 0,01 = 0; 6) 0,04x 2 1 0.
z 2 0; 4) x2 – 0,01 = 0; 6) 0,04x 2 1 0.
|
601.° Розв’яжіть рівняння: |
|
|
1) c2 – 0,25 = 0; 2) 81x2 – 121 = 0; |
3) –0,09 + 4x2 = 0. |
602.• Розкладіть на множники, користуючись формулою різниці квадратів:
|
1) (x 2)2 49; |
6) (8y + 4)2 – (4y – 3)2; |
|
2) (x −10)2 −25y 2; |
7) (5a + 3b)2 – (2a – 4b)2; |
|
3) 25 −(y −3)2; |
8) 4 (a – b)2 – (a + b)2; |
|
4) (a 4)2 (a 2)2; |
9) (x2 + x + 1)2 – (x2 – x + 2)2; |
|
5) (m −10)2 −(n −6)2; |
10) ( 3x 3 y)2 16x 6. |
603.• Подайте у вигляді добутку вираз:
1) (x −2)2 −4; 4) a 4 −(7b−a2)2;
2) (b + 7)2 – 100c2; 5) (4x 9)2 (2x 19)2; 3) 121 – (b + 7)2; 6) (a b c)2 (a b c)2.
604.• Знайдіть значення виразу:
1) (9x – 4)2 – (7x + 5)2, якщо x = 1,5;
2) (5x + 3y)2 – (3x + 5y)2, якщо x = 2,1, y = 1,9.
![]() 605.• Знайдіть значення виразу (2,5a – 1,5b)2 – – (1,5a – 2,5b)2, якщо a = –1,5, b = –3,5.
605.• Знайдіть значення виразу (2,5a – 1,5b)2 – – (1,5a – 2,5b)2, якщо a = –1,5, b = –3,5.
¿ 606.• Чому дорівнює площа заштрихованої фігури, зображеної на рисунку 7? Обчисліть значення отриманого виразу при a = 7,4 см, b = 2,6 см.
¿ 607.• Два кола, радіуси яких дорівнюють R і r (R > r), мають спільний центр. Виразіть через p, R і r площу фігури, обмеженої цими колами. Обчисліть значення отриманого виразу при R = 5,1 см, Рис. 7 r = 4,9 см.
608.• Подайте у вигляді добутку трьох множників вираз:
1) m4 – 625; 3) 24n – 16, де n — натуральне число.
2) x 16 −81;
|
609.• Розкладіть на множники: |
|
|
|
|
|
1) a 8 −b8; 610.• Розв’яжіть рівняння: |
2) a16 −256. |
|
|
|
|
1) (3x – 5)2 – 49 = 0; |
3) (a 1)2 (2a |
9)2 |
0; |
|
|
2) (4x 7)2 9x 2 0; 611.• Розв’яжіть рівняння: |
4) 25 (3b 1)2 |
16 (2b |
1)2 |
0. |
|
1) 16 (6 11x)2 0; |
2) (7m 13)2 (9m 19)2 |
0. |
||
612.• Доведіть, що при будь-якому натуральному n значення виразу:
1) (7n 4)2 9 ділиться націло на 7;
2) (8n 1)2 (3n 1)2 ділиться націло на 11;
3) (3n 7)2 (3n 5)2 ділиться націло на 24; 4) (7n 6)2 (2n 9)2 ділиться націло на 15.
613.• Доведіть, що при будь-якому натуральному n значення виразу:
1) (5n 4)2 (5n 4)2 ділиться націло на 80; 2) (9n 10)2 (9n 8)2 ділиться націло на 36; 3) (10n 2)2 (4n 10)2 ділиться націло на 12.
614.•• Доведіть, що:
1) різниця квадратів двох послідовних натуральних чисел дорівнює сумі цих чисел;
2) різниця квадратів двох послідовних парних чисел ділиться націло на 4.
615.•• Доведіть, що:
1) різниця квадратів двох послідовних парних чисел дорівнює подвоєній сумі цих чисел;
2) різниця квадратів двох послідовних непарних чисел ділиться націло на 8.
616.•• Доведіть тотожність
(m 3 n 3)2 (m 3 n 3)2 (m 6 n 6)2 4m 6n 6.
617.•• Різниця квадратів двох двоцифрових чисел, записаних одними й тими самими цифрами, дорівнює 693. Знайдіть ці числа.
618.•• Остача при діленні на 7 одного натурального числа дорівнює 4, а другого числа — 3. Доведіть, що різниця квадратів цих чисел кратна 7.
619.•• При якому значенні b рівняння (b2 4) x b 2:
1) має безліч коренів; 2) не має коренів;
3) має один корінь?
620.•• При якому значенні a рівняння (a 2 25) x a 5:
1) має безліч коренів; 2) не має коренів; 3) має один корінь?
![]()
621. У магазині «Стиль» ціну костюма знизили спочатку на 10 %, а потім ще на 10 %. У магазині «Мода» ціну такого самого костюма одразу знизили на 20 %. У якому магазині вигідніше купити костюм, якщо спочатку ціна костюма в обох магазинах була однаковою?
622. Човен рухався 2,4 год за течією річки та 3,6 год проти течії. Відстань, яку пройшов човен за течією, на 5,4 км більша за відстань, пройдену проти течії. Знайдіть власну швидкість човна, якщо швидкість течії становить 2,5 км/год.
623. За 3 дні продали 130 кг апельсинів. Другого дня продали ![]() того, що продали за перший день, а третього — стільки ж, скільки за перші два дні разом. Скільки кілограмів апельсинів продали за перший день?
того, що продали за перший день, а третього — стільки ж, скільки за перші два дні разом. Скільки кілограмів апельсинів продали за перший день?
624. У послідовності ..., a, b, c, d, 0, 1, 1, 2, 3, 5, 8, ... кожне число дорівнює сумі двох попередніх. Чому дорівнює число a?
625. Розв’яжіть рівняння:
2x 1 x 2 x ; 2) 3 (2x + 3) – 2 (3x + 5) = –1.
1)
8 4
626. Для пари виразів знайдіть усі значення a, при яких значення другого виразу в 3 рази більше за відповідне значення першого виразу:
1) a і 3a; 2) a2 і 3a 2; 3) a 2 +1 і 3a 2 +3.
![]() ГОТУЄМОСЯ ДО ВИВЧЕННЯ НОВОЇ ТЕМИ
ГОТУЄМОСЯ ДО ВИВЧЕННЯ НОВОЇ ТЕМИ
627. Запишіть у вигляді виразу:
1) квадрат суми чисел a і b;
2) суму квадратів чисел a і b; 3) подвоєний добуток чисел a і b;
4) квадрат різниці одночленів 3m і 4n.
628. Знайдіть подвоєний добуток одночленів:
1) a2 і 3b; 2) 5x і 6y; 3) 0,5m і 4n; 4) ![]() m 2 і 6m.
m 2 і 6m.
 УЧИМОСЯ РОБИТИ НЕСТАНДАРТНІ КРОКИ
УЧИМОСЯ РОБИТИ НЕСТАНДАРТНІ КРОКИ
629. Меню складається зі 101 страви. Доведіть, що кількість способів вибору обіду з непарної кількості страв дорівнює кількості способів вибору обіду з парної кількості страв за умови, що замовити всі страви з меню не можна.
![]() 16. Квадрат суми та квадрат різниці двох виразів
16. Квадрат суми та квадрат різниці двох виразів
Перетворимо в многочлен вираз (a + b)2. Маємо:
(a b)2 (a b) (a b) a2 ab ba b2 a 2 2ab b2.
Отже,
|
(a |
b)2 |
a 2 |
2ab |
b2 |
Цю тотожність називають формулою квадрата суми двох виразів. Тепер можна сформулювати правило.
Квадрат суми двох виразів дорівнює квадрату першого виразу плюс подвоєний добуток першого й другого виразів плюс квадрат другого виразу.
Перетворимо в многочлен вираз (a −b)2. Маємо:
(a b)2 (a b) (a b) a 2 ab ba b2 a 2 2ab b2.
Ми отримали формулу квадрата різниці двох виразів:
|
(a |
b)2 |
a 2 |
2ab |
b2 |
Квадрат різниці двох виразів дорівнює квадрату першого виразу мінус подвоєний добуток першого й другого виразів плюс квадрат другого виразу.
Зауважимо, що формулу квадрата різниці двох виразів можна отримати, використовуючи формулу квадрата суми двох виразів:
(a b)2 (a ( b))2 a 2 2a ( b) ( b)2 a2 2ab b2.
За допомогою отриманих формул можна простіше підносити до квадрата суму або різницю будь-яких двох виразів, не застосовуючи правила множення двох многочленів. Тому їх відносять до формул скороченого множення.
![]() ПРИКЛАД 1 Подайте у вигляді многочлена вираз:
ПРИКЛАД 1 Подайте у вигляді многочлена вираз:
1) (3b – 4c)2; 2) (a3 + 5a)2.
Розв’язання. 1) За формулою квадрата різниці двох виразів отримуємо:
(3b – 4c)2 = (3b)2 – 2æ3bæ4c + (4c)2 = 9b2 – 24bc + 16c2. 2) За формулою квадрата суми двох виразів отримуємо:
![]() (a3 + 5a)2 = (a3)2 + 2æa3æ5a + (5a)2 = a6 + 10a4 + 25a2. ¤
(a3 + 5a)2 = (a3)2 + 2æa3æ5a + (5a)2 = a6 + 10a4 + 25a2. ¤
![]() ПРИКЛАД 2 Перетворіть у многочлен вираз:
ПРИКЛАД 2 Перетворіть у многочлен вираз:
1) (–a – b)2; 2) (–x2 – 6)2.
Розв’язання. 1) Маємо: (–a – b)2 = (–a)2 – 2 (–a)æb + b2 = = a2 + 2ab + b2.
Цей приклад можна розв’язати інакше.
Оскільки (–a – b)2 = (–1æ(a + b))2 = (–1)2æ(a + b)2 = (a + b)2, тобто вирази (–a – b)2 і (a + b)2 тотожно рівні, то маємо:
(–a – b)2 = (a + b)2 = a2 + 2ab + b2.
2) ![]() (–x2 – 6)2 = (x2 + 6)2 = x4 + 12x2 + 36. ¤
(–x2 – 6)2 = (x2 + 6)2 = x4 + 12x2 + 36. ¤
![]() ПРИКЛАД 3 Розв’яжіть рівняння (x – 10)2 = (x + 7)2 – 17.
ПРИКЛАД 3 Розв’яжіть рівняння (x – 10)2 = (x + 7)2 – 17.
Розв’язання. Маємо:
x2 – 20x + 100 = x2 + 14x + 49 – 17;
x2 – 20x – x2 – 14x = 49 – 17 – 100;
–34x = –68; x = 2.
![]() Відповідь: 2. ¤
Відповідь: 2. ¤
|
Розв’язання. Нехай n — деяке натуральне число. Розглянемо три випадки. 1) Число n кратне 3. Тоді n = 3k, де k — натуральне число. Маємо: n2 = (3k)2 = 9k2. Значення виразу 9k2 кратне 3, тобто остача при діленні n2 на 3 дорівнює 0. 2) Остача при діленні на 3 числа n дорівнює 1. Тоді n можна подати у вигляді n = 3k + 1, де k — натуральне число. Маємо: n2 = (3k + 1)2 = 9k2 + 6k + 1 = 3 (3k2 + 2k) + 1 = 3p + 1, де p = 3k2 + 2k — неповна частка при діленні n2 на 3, а остача при цьому дорівнює 1. 3) |
1. Яку тотожність називають формулою квадрата суми двох виразів?
2. Сформулюйте правило піднесення до квадрата суми двох виразів.
3. ![]() Яку тотожність називають формулою квадрата різниці двох виразів?
Яку тотожність називають формулою квадрата різниці двох виразів?
4. Сформулюйте правило піднесення до квадрата різниці двох виразів.
ВПРАВИ
630.° Чи є даний вираз квадратом суми або квадратом різниці двох виразів:
1) (a + 50)2; 3) (5 – x)2; 5) (xy + mn)2; 2) a2 + b2; 4) m2 – n2; 6) (6 – c)3?
631.° Якому з наведених многочленів тотожно дорівнює вираз (5a +3)2:
1) 25a 2 +15a +9; 2) 25a 2 +30a +9; 3) 25a 2 +9; 4) 5a 2 +3?
632.° Яка з даних рівностей є тотожністю:
1) (12a b)2 144a 2 b2;
2) (12a b)2 144a 2 24ab b2; 3) (12a b)2 144a 2 24ab b2; 4) (12a b)2 12a 2 24ab b2 ?
633.° Подайте у вигляді многочлена вираз:
1) (a + x)2; 3) (y −1)2; 5) (y −13)2;
2) (x +2)2; 4) (5 − p)2; 6) (13 − y) .2
634.° Виконайте піднесення до квадрата:
1) (a +8)2; 3) (7 + c)2; 5) (6 −d)2;
2) (b −2)2; 4) (4 +k)2; 6) (d – 6)2.
635.° Закінчіть піднесення двочлена до квадрата:
1) (3x 5y)2 (3x)2 2 3æ xæ5y (5y)2 ...;
22
2) ![]() a 6b
a 6b ![]() a 2æ
a 2æ![]() a bæ6 (6b)2 ...;
a bæ6 (6b)2 ...;
3) ![]()
![]() 1 x 4 0 6, y 5 2x 4 2 2æx 4 æ0 6, y 5 (0 6, y5 )2 ... .
1 x 4 0 6, y 5 2x 4 2 2æx 4 æ0 6, y 5 (0 6, y5 )2 ... .
3
636.° Закінчіть піднесення двочлена до квадрата:
1) (ab 9)2 (ab)2 2æabæ9 92 ...;
2) (4a 2 a 3 )2 (4a 2)2 2 4æ a2 æa3 (a3 )2 ... .
637.° Подайте у вигляді многочлена вираз:
2
1) (3a −2)2; 5) 3a ![]() b ; 9) (a3 −4b)2;
b ; 9) (a3 −4b)2;
|
2) (7b +6)2; |
6) (b2 −11)2; |
10) (a 2 + a)2; |
|
3) (8x +4y)2; |
7) (a 2 +4b)2; |
11) (3b2 −2b5 )2 ; |
2
4) (0,4m −0,5n)2; 8) (x 2 + y 3)2; 12) 1![]() ab
ab ![]() c .
c .
638.° Виконайте піднесення до квадрата:
2
1) (2m +1)2; 5) 4x ![]() y ; 9) (m 2 −3n)2;
y ; 9) (m 2 −3n)2;
|
2) (4x −3)2; 6) (0,3a +0,9b)2; 10) (m 4 −n 3)2; 3) (5m −4n)2; 7) (c2 −6)2; 11) () .5a4 − 2a7 2 4) (10c +7d)2; 8) (15 +k 2)2; |
|
|
|
639.° Спростіть вираз: |
|
|
|
1) a 2 (3a b)2; |
6) 3m (m 4) (m 2)2; |
|
|
2) (4x 5)2 40x ; |
7) (y 9)2 (4 y) (y 6); |
|
|
3) 50a 2 −(7a −1)2; |
8) (x 4) (x 4) (x 1)2; |
|
|
4) c2 36 (c 6)2; |
9) (2a 3b)2 (3a 2b)2; |
|
|
5) (x 2)2 x (x 10); 640.° Спростіть вираз: |
10) (x 5)2 (x 7) (x 7). |
|
|
1) (x – 12)2 + 24x; |
4) (y 7)2 (y 2) (y 7); |
|
|
2) (x 8)2 x (x 5); |
5) (a 1) (a 1) (a 4)2; |
|
|
3) 2x (x 2) (x 2)2; 641.° Розв’яжіть рівняння: |
6) (x 10) (9 x) (x 10)2. |
|
|
1) (x 8)2 x (x 6) 2; |
3) (2x 1)2 (2x 1) (2x 3) |
0; |
|
2) (x 7)2 (x 3) (x 3); |
4) x (x 2) (x 5)2 35. |
|
642.° Розв’яжіть рівняння:
1) (x 9)2 x (x 8) 1;
2) (x – 11)2 = (x – 7) (x – 9); 3) (x – 4) (x + 4) – (x + 6)2 = –16;
4) (1 3x)2 x (9x 2) 5.
643.• Замініть зірочки такими одночленами, щоб утворилася тотожність:
1) (* b)2 * 4ab b2; 3) (* 5c)2 * 20b2c 25c2; 2) (4x *)2 16x 2 * 100y 2; 4) (7a 2 *)2 * * 9b6. 644.• Замініть зірочки такими одночленами, щоб утворилася тотожність:
1) (* 6b)2 * 24ab *; 2) (* *)2 9m 4 42m 2n 8 *.
645.• Доведіть тотожність (a b)2 (b a)2.
646.• Перетворіть у многочлен вираз:
1) ( x 1)2; 3) ( 5a 3b)2; 5) (–0,7c – 10d)2;
2
2) (−m −9)2; 4) (–4x – 8y)2; 6) 4a 2 ![]() ab .
ab .
647.• Виконайте піднесення до квадрата:
1) ( 3m 7n)2; 3) (−x 2 − y)2;
2) (–0,4x – 1,5y)2; 4) ( a 2b2 c10)2.
648.• Виконайте піднесення до квадрата:
2
1) (10a 2 −7ab2)2; 5) 1![]() a2b 2
a2b 2![]() ab2 ;
ab2 ;
2
2) (0,8b3 +0,2b2c4)2; 6) 2![]() x 3y 2
x 3y 2 ![]() y 8x ;
y 8x ;
2
3) (30m 3n +0,04n 2)2; 7) 15m 9 ![]() m 3 ;
m 3 ;
2
4) (0,5x 4y 5 −20y 6)2; 8) 3![]() x 8y 10
x 8y 10 ![]() x 2y 6 .
x 2y 6 .
649.• Перетворіть у многочлен вираз:
1) 6 (1 −2c)2; 5) (a 3) (a 4)2;
2
2) 12 x ![]() y ; 6) (2x 4)2 (x 8);
y ; 6) (2x 4)2 (x 8);
|
3) a (a −6b)2; |
7) (a |
5)2 (a 5)2; |
|
4) 5b (b2 +7b)2; |
8) (3x |
4y)2 (3x 4y)2. |
650.• Подайте у вигляді многочлена вираз:
1) (0,02p3k +20p2k 4)2; 4) 7x (x 3 −2x)2;
2
2) 1![]() mn
mn ![]() m 2n 5 ; 5) (5y 2)2 (2y 1);
m 2n 5 ; 5) (5y 2)2 (2y 1);
2
3) 15 ![]() a
a ![]() b ; 6) (10p k)2 (10p k)2.
b ; 6) (10p k)2 (10p k)2.
651.• Спростіть вираз і знайдіть його значення:
1) (a 3)2 (a 9) (a 9), якщо a = –2,5;
2) (5x 8)2 (4x 3)2 26x, якщо x ![]() ;
;
3) (3y 2 4)2 (3y 2 4)2 2 (1 3y 2) (1 3y 2), якщо y = ![]() .
.
652.• Спростіть вираз і знайдіть його значення:
1) 2m (m −6)2 −m 2 (2m −15), якщо m = –4; 2) (2x 5)2 4 (x 1) (x 7), якщо x = –3,5.
653.• При якому значенні змінної значення квадрата двочлена x + 12 на 225 більше за відповідне значення квадрата двочлена x – 13?
654.• Розв’яжіть рівняння:
1) (x – 12) (x + 12) = 2 (x – 6)2 – x2;
2) (3x 1)2 (4x 2)2 (5x 1) (5x 1); 3) 5 (x 2)2 (2x 1)2 9 (x 3) (x 3) 22.
655.• Розв’яжіть рівняння:
1) (3x 2)2 (4x 1) (4x 1) (5x 1)2;
2) 2 (m + 1)2 + 3 (m – 1)2 – 5 (m + 1) (m – 1) = –4.
¿ 656.• Знайдіть сторону квадрата, якщо при збільшенні її на 5 см отримаємо квадрат, площа якого на 95 см2 більша за площу даного.
¿ 657.• Якщо сторону квадрата зменшити на 8 см, то отримаємо квадрат, площа якого на 352 см2 менша від площі даного. Знайдіть сторону даного квадрата.
658.• Знайдіть три послідовних натуральних числа, якщо подвоєний квадрат більшого з них на 79 більший за суму квадратів двох інших чисел.
659.• Знайдіть чотири послідовних натуральних числа, якщо сума квадратів другого й четвертого з них на 82 більша за суму квадратів першого й третього.
660.• При яких значеннях a і b є правильною рівність:
1) (a b)2 a 2 b2; 2) (a b)2 (a b)2 ?
661.• Доведіть тотожність:
1) (a b)2 (a b)2 2 (a2 b2);
2) (a b)2 (a b)2 4ab;
3) a 2 b2 (a b)2 2ab;
|
4) (a 2 b2) (c2 d 2) (ac bd)2 662.• Доведіть тотожність: 1) a 2 b2 (a b)2 2ab; |
(ad |
bc)2. |
|
2) (a b)2 (ab 1)2 (a 2 1) (b2 |
1). |
|
663.• Доведіть, що значення виразу не залежить від значення змінної:
1) (x 3)2 (x 3)2 2 (x 6) (x 6); 2) (4x 3 5)2 (2x 3 1)2 4 (5x 3 4) (x 3 1).
664.• Доведіть, що значення виразу не залежить від значення змінної x:
1) (6x – 8)2 + (8x + 6)2 – (10x – 1) (10x + 1);
2) 2 (4x y) (8x 5y) (8x 5y)2 4y (26x 1).
665.• Яким числом, парним чи непарним, є квадрат непарного натурального числа?
666.• Виведіть формулу куба суми двох виразів:
(a b)3 a 3 3a2b 3ab2 b3.
Користуючись цією формулою, перетворіть у многочлен вираз:
1) (x +3)3; 2) (2x + y)3.
667.• Виведіть формулу куба різниці двох виразів:
(a b)3 a 3 3a 2b 3ab2 b3.
Користуючись цією формулою, перетворіть у многочлен вираз:
1) (1 −x)3; 2) (x −5y)3.
668.• Виведіть формулу квадрата тричлена:
(a b c)2 a 2 b2 c2 2ab 2bc 2ac.
Користуючись цією формулою, перетворіть у многочлен вираз:
1) (a b c)2; 2) (a b 4)2.
669.• Давньогрецький учений Евклід (ІІІ ст. до н. е.) доводив формули квадрата суми та квадрата різниці двох виразів геометрично. Користуючись рисунками 8 і 9, відтворіть його доведення.
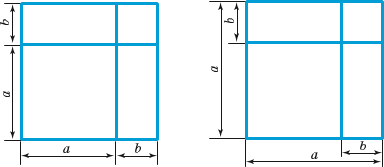
Рис. 8 Рис. 9
670.•• Чому дорівнює остача при діленні квадрата непарного натурального числа на 8?
671.•• З’ясуйте, яку остачу може давати квадрат натурального числа при діленні на 4.
672.•• Доведіть, що різниця між сумою квадратів двох послідовних цілих чисел та їхнім подвоєним добутком не залежить від вибору чисел.
673.•• Доведіть, що коли остача при діленні натурального числа на 16 дорівнює 4, то квадрат цього числа ділиться націло на 16.
674.•• Доведіть, що коли остача при діленні натурального числа на 25 дорівнює 5, то квадрат цього числа кратний 25.
675.•• Остача при діленні деякого натурального числа на 9 дорівнює 5. Чому дорівнює остача при діленні на 9 квадрата цього числа?
676.•• Остача при діленні деякого натурального числа на 11 дорівнює 6. Чому дорівнює остача при діленні на 11 квадрата цього числа?
677.•• Використовуючи формули скороченого множення, подайте у вигляді многочлена вираз:
1) (a + b + c) (a + b – c); 3) (a + b + c + d) (a + b – c – d). 2) (a + b + c) (a – b – c);
678.•• Використовуючи формули скороченого множення, подайте у вигляді многочлена вираз:
1) (a – b – c) (a + b – c); 2) (a – b + c + d) (a – b – c – d).
679.•• При якому значенні a рівняння (6x a)2 (8x 3)2 (10x 3)2 не має коренів?
680.•• При якому значенні a рівняння
(2a – 3x)2 + (x – 1)2 = 10 (x – 2) (x + 2)
не має коренів?
681.* Доведіть тотожність
(2n 1)2 (2n 2 2n)2 (2n 2 2n 1)2.
Наведена тотожність є правилом великого давньогрецького вченого Піфагора (VI ст. до н. е.) для обчислення цілочислових значень довжин сторін прямокутного трикутника. При одному й тому самому натуральному значенні n значення виразів 2n + 1; 2n2 + 2n; 2n2 + 2n + 1 є довжинами сторін прямокутного трикутника.
682.* (Тотожність Ж. Л. Лагранжа[4].) Доведіть тотожність
(a 2 b2 c2) (m 2 n 2 k 2) (am bn ck)2 (an bm)2 (ak cm)2 (bk cn)2.
683.* Доведіть, що сума квадратів п’яти послідовних натуральних чисел не може дорівнювати квадрату натурального числа.
![]()
684. ![]() Цукровий буряк є найсолодшою коренеплідною рослиною, яку вирощують в Україні. У ньому накопичується до 25 % цукру, тоді як у цукровій тростині — лише 18 %. Скільки тонн цукрової тростини треба переробити, щоб отримати стільки ж цукру, скільки одержують із 3600 т цукрових буряків?
Цукровий буряк є найсолодшою коренеплідною рослиною, яку вирощують в Україні. У ньому накопичується до 25 % цукру, тоді як у цукровій тростині — лише 18 %. Скільки тонн цукрової тростини треба переробити, щоб отримати стільки ж цукру, скільки одержують із 3600 т цукрових буряків?
685. У 2017 р. в місті Києві працювало 28 історичних, літературних і мистецьких музеїв. Мистецьких музеїв було в 3,4 раза менше, ніж історичних, і на один музей менше, ніж
літературних. Скільки працювало Національний музей музеїв кожного із цих трьох видів? історії України (м. Київ)
686. До магазину завезли 740 кг апельсинів і бананів у 80 ящиках. У кожному ящику було 10 кг апельсинів або 8 кг бананів. Скільки кілограмів апельсинів завезли до магазину?
687. У першій коробці було 45 кульок, з них 15 — білих; у другій — 75 кульок, з них 25 — білих; у третій — 24 білих і 48 червоних кульок; у четвертій — порівну білих, червоних і зелених кульок. Для якої коробки ймовірність навмання витягнути з неї білу кульку є більшою?
688. Якого найменшого значення та при якому значенні змінної набуває вираз:
1) x 2; 2) x 2 −16; 3) (x +4)2 +20?
689. Якого найбільшого значення та при якому значенні змінної набуває вираз:
1) −x 2; 2) x 2 4; 3) 12 −(x −1)2 ?
690. При якому значенні змінної виконується рівність:
1) (x 1)2 (x 1)2 10; 3) (x 2 1)2 (x 1)2 0?
2) (x 1)2 (x 1)2 0;
Трикутник Паскаля
691. При яких значеннях змінних x і y виконується рівність:
1) (x 2)2 (y 6)2 1; 2) (x 2)2 (y 6)2 0?
 УЧИМОСЯ РОБИТИ НЕСТАНДАРТНІ КРОКИ
УЧИМОСЯ РОБИТИ НЕСТАНДАРТНІ КРОКИ
![]()
692. Відомо, що натуральні числа m і n такі, що значення виразу 10m + n ділиться націло на 11. Доведіть, що значення виразу (10m + n) (10n + m) ділиться націло на 121.
Розв’язуючи задачу 666, ви довели, що
(a + b)3 = a3 + 3a2b + 3ab2 + b3
Цю тотожність називають формулою куба суми двох виразів.
Якщо записати, що (a + b)4 = (a + b)3 (a + b), то можна перетворити в многочлен вираз (a + b)4. Отримуємо таку тотожність:
(a + b)4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4.
![]() Діючи аналогічно, можна перетворити в многочлен будь-який вираз вигляду (a + b)n. Проте зі збільшенням показника n зростатиме обсяг роботи, пов’язаної з перетвореннями виразів.
Діючи аналогічно, можна перетворити в многочлен будь-який вираз вигляду (a + b)n. Проте зі збільшенням показника n зростатиме обсяг роботи, пов’язаної з перетвореннями виразів.
Технічну роботу можна скоротити, якщо підмітити певні закономірності. Усі одночлени, які стоять у правій частині тотожності, мають однаковий степінь, що дорівнює показнику степені двочлена. Буквені частини цих одночленів відповідно мають такий вигляд: an, an – 1b, an – 2b2,
n n n
|
цієнтів цих одночленів існує спеціальна таблиця (рис. 10), яку називають «трикутником Паскаля» на честь видатного французького математика та філософа Блеза Паскаля. Тут стрілочками показано, як знайти наступний рядок таблиці за попереднім: додавши два сусідніх червоних числа, отримаємо інше червоне число, записане в наступному рядку між двома даними числами. |
Блез Паскаль (1623–1662) Французький математик, фізик, літератор і філософ. Один із засновників математичного аналізу, теорії ймовірностей і проєктивної геометрії. Створив перші зразки обчислювальної техніки. |
a– 3b3, ..., ab – 1, b . Для пошуку коефі-
Далі показано, як користуватися цією таблицею.
1
(a + b)1: 1æa1 + 1æb1
(a + b)2: 1æa2 + 2æa1b1 + 1æb2
(a + b)3: 1æa3 + 3æa2b1 + 3æa1b2 + 1æb3
(a + b)4: 1æa4 + 4æa3b1 + 6æa2b2 + 4æa1b3 + 1æb4 (a + b)5: 1æa5 + 5æa4b1 + 10æa3b2 + 10æa2b3 + 5æa1b4 + 1æb5
![]() 17. Перетворення многочлена у квадрат
17. Перетворення многочлена у квадрат
суми або різниці двох виразів
Перепишемо формули квадрата суми та квадрата різниці двох виразів, помінявши місцями їхні ліві й праві частини:
|
a 2 a 2 |
2ab 2ab |
b2 b2 |
(a (a |
b)2, b)2 |
У такому вигляді ці формули в ряді випадків дозволяють «згорнути» тричлен у квадрат двочлена.
Тричлен, який можна подати у вигляді квадрата двочлена, називають повним квадратом.
![]() ПРИКЛАД 1 Подайте тричлен у вигляді квадрата двочлена:
ПРИКЛАД 1 Подайте тричлен у вигляді квадрата двочлена:
1) x2 + 10x + 25; 2) 9a6 – 42a3b2 + 49b4.
Розв’язання. 1) x 2 10x 25 x 2 2æxæ5 52 (x 5)2.
2) ![]() 9a 6 42a 3b2 49b4 (3a 3)2 2æ3a 3æ7b2 (7b2)2 (3a 3 7b2)2.
9a 6 42a 3b2 49b4 (3a 3)2 2æ3a 3æ7b2 (7b2)2 (3a 3 7b2)2. ¤
![]() П Р И К Л А Д 2 Знайдіть, користуючись перетворенням виразу у квадрат двочлена, значення суми 5,22 +10,4æ4,8 +4,82.
П Р И К Л А Д 2 Знайдіть, користуючись перетворенням виразу у квадрат двочлена, значення суми 5,22 +10,4æ4,8 +4,82.
Розв’язання. Маємо: 5,22 10,4æ4,8 4,82
![]() 5,22 2æ5,2æ4,8 4,82 (5,2 4,8)2 102 100.
5,22 2æ5,2æ4,8 4,82 (5,2 4,8)2 102 100. ¤
![]() ПРИКЛАД 3 Розв’яжіть рівняння 4x2 – 12x + 9 = 0.
ПРИКЛАД 3 Розв’яжіть рівняння 4x2 – 12x + 9 = 0.
Розв’язання. Подамо ліву частину рівняння у вигляді квадрата різниці:
(2x – 3)2 = 0.
![]() Оскільки значення квадрата дорівнює нулю тоді й тільки тоді, коли його основа дорівнює нулю, то отримуємо: 2x – 3 = 0; x = 1,5. Відповідь: 1,5.
Оскільки значення квадрата дорівнює нулю тоді й тільки тоді, коли його основа дорівнює нулю, то отримуємо: 2x – 3 = 0; x = 1,5. Відповідь: 1,5. ¤
![]() ПРИКЛАД 4 Доведіть, що значення виразу
ПРИКЛАД 4 Доведіть, що значення виразу
(2x + 1)2 – 2 (2x + 1) (2x – 5) + (2x – 5)2
не залежить від значення змінної.
Розв’язання. Маємо: (2x + 1)2 – 2 (2x + 1) (2x – 5) + (2x – 5)2 =
![]() = ((2x + 1) – (2x – 5))2 = (2x + 1 – 2x + 5)2 = 62 = 36.
= ((2x + 1) – (2x – 5))2 = (2x + 1 – 2x + 5)2 = 62 = 36. ¤
![]() ПРИКЛАД 5 Доведіть, що вираз x2 – 4x + 5 набуває додатних значень при будь-яких значеннях x. Якого найменшого значення набуває вираз і при якому значенні x?
ПРИКЛАД 5 Доведіть, що вираз x2 – 4x + 5 набуває додатних значень при будь-яких значеннях x. Якого найменшого значення набуває вираз і при якому значенні x?
Розв’язання. Перетворимо даний вираз:
x2 – 4x + 5 = x2 – 4x + 4 + 1 = (x – 2)2 + 1.
Подання виразу у вигляді суми, одним із доданків якої є квадрат двочлена (у нашому прикладі це (x – 2)2), називають виділенням квадрата двочлена з даного виразу.
Оскільки (x −2)2 l0 при будь-яких значеннях x, то вираз
![]() (x – 2)2 + 1 набуває лише додатних значень. Також зрозуміло, що (x – 2)2 + 1 l 1. Звідси найменшого значення, яке дорівнює 1, даний вираз набуває при x = 2.
(x – 2)2 + 1 набуває лише додатних значень. Також зрозуміло, що (x – 2)2 + 1 l 1. Звідси найменшого значення, яке дорівнює 1, даний вираз набуває при x = 2. ¤
![]() ПРИКЛАД 6 При яких значеннях x і y значення многочлена x2 + y2 – 12x + 4y + 40 дорівнює нулю?
ПРИКЛАД 6 При яких значеннях x і y значення многочлена x2 + y2 – 12x + 4y + 40 дорівнює нулю?
Розв’язання. Маємо: x2 + y2 – 12x + 4y + 40 = = x2 – 12x + 36 + y2 + 4y + 4 = (x – 6)2 + (y + 2)2.
Ми подали даний многочлен у вигляді суми двох доданків, які можуть набувати лише невід’ємних значень. Їхня сума, а отже, і даний многочлен набуватимуть нульового значення тоді й тільки тоді, коли кожен із доданків дорівнюватиме нулю, тобто коли x = 6 і y = –2.

693.° Якому з наведених виразів тотожно дорівнює многочлен a 2 18a 81:
1) (a −3)2; 3) (a – 9) (a + 9); 2) a – 9; 4) (a −9)2 ?
694.° Яка з даних рівностей є тотожністю:
1) a 2 8ab 16b2 (a 8b)2; 3) a 2 8ab 16b2 (ab 4)2; 2) a 2 8ab 16b2 (a 4b)2; 4) a2 8ab 16b2 (a 2b)2 ?
695.° Подайте тричлен у вигляді квадрата двочлена:
1) c2 + 2cd + d2; 2) p2 – 2pq + q2; 3) x 2 2æ æx 7 72.
696.° Розкладіть на множники многочлен:
1) m2 + 2mn + n2; 2) b2 – 2bc + c2; 3) 112 2 11æ æp p2.
¿ 697.° Подайте многочлен у вигляді квадрата суми або квадрата різниці двох виразів:
|
1) a 2 +2a +1; |
7) b4 2b2c c2; |
|
2) x 2 12x 36; |
8) m 8 +m 4n 2 + 1 n 4; 4 |
|
3) y 2 18y 81; |
9) 36a 2b2 12ab 1; |
|
4) 100 20c c2; |
10) x 4 +2x 2 +1; |
5) a 2 6ab 9b2; 11) ![]() x 4 2x 2y 3 16y 6;
x 4 2x 2y 3 16y 6;
6) 9a2 – 30ab + 25b2; 12) 0,01a 8 25b14 a 4b7.
698.° Подайте тричлен у вигляді квадрата двочлена:
|
1) b2 2b 1; |
5) 9x 2 24xy 16y 2; |
|
2) 4 +4n +n 2; |
6) a 6 2a 3 1; |
|
3) x 2 14x 49; |
7) 36a6 84a 3b5 49b10; |
|
4) 4a 2 +4ab+b2; |
8) 81x 4y 8 36x 2y 4z 6 4z12. |
699.° Знайдіть значення виразу, подавши його попередньо у вигляді квадрата двочлена: 1) y 2 8y 16, якщо y = –4;
2) c2 +24c +144, якщо с = –10;
3) 25x 2 20xy 4y 2, якщо x = 3, y = 5,5;
4) 49a 2 +84ab+36b2, якщо a =1![]() , b =2
, b =2![]() .
.
700.° Знайдіть значення виразу:
1) b2 30b 225, якщо b = 6;
2) 100a2 +60ab+9b2, якщо a = 0,8, b = –3.
701.• Який одночлен треба поставити замість зірочки, щоб можна було подати у вигляді квадрата двочлена вираз:
|
1) * – 56a + 49; |
5) a2b2 4a 3b5 *; |
|
2) 9c2 12c *; |
6) 1,44x 2y 4 *y 0,25y 6; |
|
3) * – 42xy + 49y2; |
7) 64 – 80y20 + *y40; |
4) 0,01b2 +* +100c2; 8) ![]() a6b2 a5b5 *?
a6b2 a5b5 *?
702.• Замініть зірочки такими одночленами, щоб виконувалася тотожність:
1) n 2 60n * (* 30)2; 3) 225a 2 * 64b4 (* *)2; 2) 25c2 * * (* 8k)2; 4) 0,04x 2 * * (* 0,3y 3)2.
703.• Подайте, якщо це можливо, у вигляді квадрата двочлена або у вигляді виразу, протилежного квадрату двочлена, тричлен:
1) –8x + 16 + x2; 5) 81c2 – 54b2c + 9b2;
2) a8 + 4a4b3 + 4b6; 6) b10 – a2b5 + 0,25a4;
3) 2x −25 −0,04x 2; 7) ![]() x 2 xy 4y 2;
x 2 xy 4y 2;
4) 25m 2 30mn 9n 2; 8) − 9 n 6 −3mn 5 −16m 2n 4.
64
704.• Подайте, якщо це можливо, у вигляді квадрата двочлена або у вигляді виразу, протилежного квадрату двочлена, тричлен:
1) −a 4 −0,8a 6 −0,16a 8; 4) ![]() a 8 10a 4b6 49b12;
a 8 10a 4b6 49b12;
2) 121m 2 44mn 16n 2; 5) 80xy +16x 2 +25y 2;
3) a 6 4a 3b 4b2; 6) b10 ![]() b5c
b5c ![]() c2.
c2.
705.• Подайте у вигляді квадрата двочлена вираз:
1) (4a 3b)2 8b (4a b); 2) (10x 3y)2 (8x 4y) (8x 4y).
706.• Перетворіть у квадрат двочлена вираз:
1) (3m 2n)2 5m (4n m); 2) (9x 2y)2 (8x 3y) (4x 4y).
707.• Користуючись перетворенням виразів у квадрат суми або різниці двох чисел, знайдіть значення даного виразу:
1) 1,022 – 1,02æ1,96 + 0,982; 2) 242 + 96æ38+762.
708.• Обчисліть:
1) 2032 – 406æ103 + 1032; 2) 1,582 + 1,58æ2,84 + 1,422.
709.• Яке число треба додати до многочлена 81a2b2 – 36ab + 9, щоб отриманий вираз тотожно дорівнював квадрату двочлена?
710.• Яке число треба додати до многочлена 100m4 + 120m2 + 40, щоб отриманий вираз тотожно дорівнював квадрату двочлена?
711.• Розв’яжіть рівняння:
1) x2 – 16x + 64 = 0; 2) 81x2 + 126x + 49 = 0.
712.• Розв’яжіть рівняння:
1) x2 + 12x + 36 = 0; 2) 25x2 – 30x + 9 = 0.
713.• Чи є тотожністю рівність
(a 2) (a 3) (a 3) (a 2) a 2 (a 2 6)2 ?
714.• Доведіть тотожність:
1) (a 1)2 2 (a 1) 1 a 2;
2) (a b)2 2 (a b) (a b) (a b)2 4b2;
3) (a – 8)2 + 2 (a – 8) (3 – a) + (a – 3)2 = 25;
4) (x n 2)2 2 (x n 2) (x n 2) (x n 2)2 16, де n — довільне натуральне число.
715.• Доведіть, що значення виразу не залежить від значення змінної:
1) (3x 8)2 2 (3x 8) (3x 8) (3x 8)2;
2) (4x 7)2 (4x 11)2 2 (4x 7) (11 4x).
716.•• Доведіть, що не має коренів рівняння:
1) x 2 14x 52 0; 2) 4x 2 2x 1 0.
717.•• Доведіть, що даний вираз набуває додатних значень при всіх значеннях x. Укажіть, якого найменшого значення набуває цей вираз і при якому значенні x:
1) x 2 6x 10; 2) 16x 2 +24x +25; 3) x 2 + x +1.
718.•• Чи може набувати від’ємних значень вираз:
1) x 2 24x 144; 2) 4x 2 +20x +28?
719.•• Доведіть, що даний вираз набуває від’ємних значень при всіх значеннях x. Укажіть, якого найбільшого значення набуває цей вираз і при якому значенні x:
1) x 2 4x 12; 2) 22x −121x 2 −2; 3) −56 −36x 2 −84x.
720.•• Чи може набувати додатних значень вираз:
1) x 2 20x 100; 2) −x 2 −10 −4x ?
721.•• Якого найбільшого значення та при якому значенні змінної набуває вираз:
1) x 2 16x 36; 2) 2 16x 2 24x ?
722.•• Якого найменшого значення та при якому значенні змінної набуває вираз:
1) x 2 28x 200; 2) 9x 2 30x 25?
723.•• Подайте многочлен ![]() x 4 y 8
x 4 y 8 ![]() x 2y 4 у вигляді добутку квадратів двох двочленів.
x 2y 4 у вигляді добутку квадратів двох двочленів.
724.•• Доведіть, що вираз (a – 3b) (a – 3b – 4) + 4 набуває невід’ємних значень при будь-яких значеннях змінних.
725.•• Подайте у вигляді суми квадратів двох виразів многочлен:
1) 2a 2 2a 1; 4) 10x 2 6xy y 2; 2) a 2 +b2 +2a +2b+2; 5) x 2 5y 2 4xy 4y 4; 3) x 2 6x y 2 2y 10; 6) 2a 2 +2b2.
726.•• Розкладіть на множники многочлен, попередньо подавши його у вигляді різниці квадратів двох виразів: 1) a4 + a2 + 1; 3) a2b2 + 2ab – c2 – 8c – 15; 2) x2 – y2 + 4x – 4y; 4) 8a2 – 12a + 2ab – b2 + 4.
727.•• Подайте многочлен у вигляді суми або різниці квадратів двох виразів:
1) a4 + 17a2 + 16; 3) 2x2 – 6xy + 9y2 – 6x + 9; 2) x2 + y2 – 10x + 14y + 74; 4) x2 – y2 – 4x – 2y + 3.
728.•• При яких значеннях x і y дорівнює нулю значення многочлена:
1) x2 + y2 + 8x – 10y + 41; 2) x2 + 37y2 + 12xy – 2y + 1?
729.•• Чи існують такі значення x і y, при яких дорівнює нулю значення многочлена:
1) x 2 4y 2 2x 4y 2; 2) 9x 2 y 2 12x 8y 21?
730.•• Значення змінних a і b є такими, що a + b = 7, ab = 2. Знайдіть значення виразу a2 + b2.
731.•• Додатні значення змінних a і b є такими, що a2 + b2 = 34, ab = 15. Знайдіть значення виразу a + b.
732.•• Від’ємні значення змінних a і b є такими, що a2 + b2 = 68, ab = 16. Знайдіть значення виразу a + b.
733.* Подайте число 24 у вигляді суми таких двох чисел, щоб їхній добуток був найбільшим.
734.* Знайдіть сторони прямокутника, що має найбільшу площу з усіх прямокутників, периметр кожного з яких дорівнює 20 см. 735.* Числа a і b такі, що b2 a2 1, ab = 3, a > 0, b > 0. Знайдіть
4
значення виразу a + 2b.
736.* Числа a, b і c такі, що a 2 b2 c2 ab ac bc 0. Чому дорівнює значення виразу a + b – 2c?
![]()
![]() ¿ 737. Для виробництва 1 т паперу потрібно використати 6,3 м3 деревини або 1400 кг макулатури. Учні та учениці школи зібрали 2100 кг макулатури. Скільки кубічних метрів деревини можна зекономити, використавши для виробництва паперу зібрану макулатуру?
¿ 737. Для виробництва 1 т паперу потрібно використати 6,3 м3 деревини або 1400 кг макулатури. Учні та учениці школи зібрали 2100 кг макулатури. Скільки кубічних метрів деревини можна зекономити, використавши для виробництва паперу зібрану макулатуру?
¿ 738. Для перевезення 30 т вантажу на відстань 80 км можна скористатися послугами однієї з трьох фірм-перевізників. Вартість перевезення та вантажопідйомність автомобілів кожної фірми наведено в таблиці.
|
Фірмаперевізник |
Вартість перевезення одним автомобілем на 10 км, грн |
Вантажопідйомність автомобіля, т |
|
А |
210 |
4 |
|
Б |
240 |
5,5 |
|
В |
360 |
10 |
Скільки гривень коштуватиме найдешевше перевезення вантажу?
739. Першого дня туристка проїхала 0,4 усього шляху, другого — ![]() решти, а третього — 20 км, що залишилися. Знайдіть дов-
решти, а третього — 20 км, що залишилися. Знайдіть дов-
жину шляху.
740. Загальна площа двох ділянок, засіяних кукурудзою, дорівнює 100 га. На першій ділянці зібрали по 90 т зеленої маси кукурудзи з 1 га, а на другій — по 80 т. Знайдіть площу кожної ділянки, якщо з першої ділянки зібрали на 2200 т більше, ніж із другої.
741. Розкладіть на множники:
1) 2ab−3ab2; 4) 2a 2b ac bc;
2) 8x 4 +2x 3; 5) m 2 mn 4m 4n;
3) 12a 2b2 +6a 2b3 +12ab3; 6) ax – ay + cy – cx – x + y.
завдання № 4 «Перевірте себе» в тестовій формі
![]()
742. При деякому значенні x значення виразу 3x 2 x 7 дорівнює 10. Якого значення набуває вираз 6x 2 2x 7 при цьому значенні x?
743. (Старовинна болгарська задача.) Сім рибалок ловили на озері рибу. Перший ловив рибу щодня, другий — через день, третій — через 2 дні й т. д., сьомий — через 6 днів. Сьогодні всі рибалки прийшли на озеро. Через яку найменшу кількість днів усі сім рибалок зберуться разом на озері?
![]() ГОТУЄМОСЯ ДО ВИВЧЕННЯ НОВОЇ ТЕМИ
ГОТУЄМОСЯ ДО ВИВЧЕННЯ НОВОЇ ТЕМИ
¿ 744. Запишіть у вигляді виразу:
1) куб суми чисел a і b; 3) різницю кубів чисел c і d; 2) суму кубів чисел a і b; 4) куб різниці чисел c і d.
745. Піднесіть до куба одночлен:
1) y 2; 3) 3a 2b4; 5) ![]() b6c7;
b6c7;
2) 2x 3; 4) 0,1mn 5; 6) ![]() p10k 15.
p10k 15.
746. Подайте у вигляді куба одночлена вираз:
1) a 3b6; 3) ![]() c9; 5) 0,216k 15 p24;
c9; 5) 0,216k 15 p24;
2) 8x 3y 9; 4) 125m12n 21; 6) 0,008a 9b18c27.
 УЧИМОСЯ РОБИТИ НЕСТАНДАРТНІ КРОКИ
УЧИМОСЯ РОБИТИ НЕСТАНДАРТНІ КРОКИ
747. Чи можна натуральні числа від 1 до 32 розбити на три групи так, щоби добутки чисел кожної групи були рівними?
ЗАВДАННЯ № 4 «ПЕРЕВІРТЕ СЕБЕ» В ТЕСТОВІЙ ФОРМІ
1. Виконайте множення: (3n + 1) (3n – 1).
А) 9n2 – 6n + 1; В) 9n2 – 1; Б) 9n2 + 6n + 1; Г) 9n2 + 1.
2. Якому многочлену дорівнює вираз (4x – 1)2?
А) 16x2 + 8x + 1; В) 16x2 + 1;
Б) 16x2 – 8x + 1; Г) 16x2 – 1.
3. Розкладіть на множники вираз 4a2 – 25.
А) (2a – 5)2; В) (2a – 5) (2a + 5);
Б) (2a + 5)2; Г) 2a (2a – 25).
4. Подайте у вигляді добутку вираз –0,09x4 + 81y16.
А) (0,03x2 – 9y4) (0,03x2 + 9y4); Б) (9y8 – 0,03x2) (9y8 + 0,03x2);
В) (9y8 – 0,3x2) (9y8 + 0,3x2);
Г) (9y4 – 0,3x2) (9y4 + 0,3x2).
5. Який із даних двочленів можна розкласти на множники, застосовуючи формулу різниці квадратів?
А) –a2 – 4b2; Б) 4a2 + b2; В) a2 – 4b2; Г) 4b2 + a2.
6. Подайте у вигляді квадрата двочлена вираз a2 – 8a + 16.
А) (a + 4)2; Б) (a – 4)2; В) (4a + 1)2; Г) (a – 1)2.
2
7. Відомо, що ![]() x 3y 2
x 3y 2 ![]() x 2 axy 2 9y 4. Чому дорівнює значення a?
x 2 axy 2 9y 4. Чому дорівнює значення a?
А) 3; Б) –3; В) 6; Г) –6.
8. Спростіть вираз (x + 8) (x – 8) – x (x – 6).
А) 6x – 16; Б) 6x + 16; В) –6x – 64; Г) 6x – 64.
9. Якому многочлену дорівнює вираз (7m – 2)2 – (7m – 1) (7m + 1)? А) –14m + 5; Б) –14m + 3; В) –28m + 5; Г) –28m + 3.
10. Спростіть вираз (c – 4)2 – (3 – c)2.
А) 2c – 7; Б) 7 – 2c; В) 7 + 2c; Г) –2c – 7.
11. Знайдіть значення виразу (x – 4)2 + 2 (4 + x) (4 – x) + (x + 4)2 при x = –1,2.
А) 64; Б) 32; В) 48; Г) 72.
12. Подайте у вигляді многочлена вираз (4 + a2) (a – 2) (a + 2). А) a2 – 16; Б) 16 – a2; В) 16 – a4; Г) a4 – 16.
![]() 18. Сума й різниця кубів двох виразів
18. Сума й різниця кубів двох виразів
Помножимо двочлен a +b на тричлен a2 ab b2. Отримаємо:
(a b) (a 2 ab b2) a 3 a 2b ab2 a 2b ab2 b3 a3 b3.
![]()
Тим самим ми довели тотожність
a 3 b3 (a b) (a 2 ab b2)
Цю тотожність називають формулою суми кубів двох виразів.
Многочлен a2 ab b2, який стоїть у правій частині, називають неповним квадратом різниці. Така назва пояснюється його зовнішньою схожістю з многочленом a 2 2ab b2, який дорівнює квадрату різниці a і b.
Тепер можна сформулювати правило.
Сума кубів двох виразів дорівнює добутку суми цих виразів і неповного квадрата їхньої різниці.
Розкладемо на множники вираз a3 −b3. Маємо:
a 3 b3 a 3 ( b)3 (a ( b)) (a 2 a ( b) ( b)2) (a b) (a 2 ab b2). Ми довели тотожність
|
a 3 |
b3 |
(a |
b) (a 2 |
ab |
b2) |
Цю тотожність називають формулою різниці кубів двох виразів.
Многочлен a2 + ab+b2 називають неповним квадратом суми.
Отже, сформулюємо правило.
Різниця кубів двох виразів дорівнює добутку різниці цих виразів і неповного квадрата їхньої суми.
Зауважимо, що цю формулу також можна довести, перемноживши многочлени, які стоять у правій частині.
![]() ПРИКЛАД 1 Розкладіть на множники:
ПРИКЛАД 1 Розкладіть на множники:
1) 8a3 + 27b3; 2) x6 – y9.
Розв’язання. 1) Подавши даний многочлен у вигляді суми кубів двох виразів, отримуємо:
8a3 + 27b3 = (2a)3 + (3b)3 = (2a + 3b) (4a2 – 6ab + 9b2).
2) Подавши даний многочлен у вигляді різниці кубів двох виразів, отримуємо:
![]() x6 – y9 = (x2)3 – (y3)3 = (x2 – y3) (x4 + x2y3 + y6). ¤
x6 – y9 = (x2)3 – (y3)3 = (x2 – y3) (x4 + x2y3 + y6). ¤
![]() ПРИКЛАД 2 Спростіть вираз (4y – 1) (16y2 + 4y + 1) і знайдіть його значення при y =
ПРИКЛАД 2 Спростіть вираз (4y – 1) (16y2 + 4y + 1) і знайдіть його значення при y = ![]() .
.
Розв’язання. Маємо: (4y – 1) (16y2 + 4y + 1) = (4y)3 – 1 = 64y3 – 1.
При y = ![]() отримуємо:
отримуємо:
3
![]() 64y 3 1 64æ
64y 3 1 64æ ![]() 1 64æ
1 64æ![]() 1 8 1 7. ¤
1 8 1 7. ¤
![]() ПРИКЛАД 3 Подайте у вигляді добутку вираз (m – 4)3 + 216.
ПРИКЛАД 3 Подайте у вигляді добутку вираз (m – 4)3 + 216.
Розв’язання. Застосувавши формулу суми кубів, отримуємо:
(m – 4)3 + 216 = (m – 4)3 + 63 =
= (m – 4 + 6) ((m – 4)2 – 6 (m – 4) + 36) =
![]() = (m + 2) (m2 – 8m + 16 – 6m + 24 + 36) = = (m + 2) (m2 – 14m + 76). ¤
= (m + 2) (m2 – 8m + 16 – 6m + 24 + 36) = = (m + 2) (m2 – 14m + 76). ¤
![]() ПРИКЛАД 4 Доведіть, що значення виразу 253 – 1 ділиться націло на 24.
ПРИКЛАД 4 Доведіть, що значення виразу 253 – 1 ділиться націло на 24.
Розв’язання. Застосувавши формулу різниці кубів, матимемо:
253 – 1 = (25 – 1) (252 + 25 + 1) = 24 (252 + 26).
Даний вираз подано у вигляді добутку, один із множників якого дорівнює 24, а другий є натуральним числом. Отже, значення цього виразу ділиться націло на 24. ¤
1. Яку тотожність називають формулою суми кубів?
2. Який многочлен називають неповним квадратом різниці?
3. Сформулюйте правило розкладання на множники суми кубів двох виразів.
4. Яку тотожність називають формулою різниці кубів?
5. Який многочлен називають неповним квадратом суми?
6. ![]() Сформулюйте правило розкладання на множники різниці кубів двох виразів.
Сформулюйте правило розкладання на множники різниці кубів двох виразів.
ВПРАВИ
748.° Який із даних виразів є неповним квадратом суми, а який — неповним квадратом різниці:
|
1) m2 + 2mn + n2; |
4) m2 – 4mn + n2; |
|
2) m2 + mn – n2; |
5) m2 – mn + n2; |
|
3) m2 + mn + n2; |
6) m2 – 2mn + n2? |
749.° Чи є тотожністю рівність:
1) x3 + y3 = (x + y) (x2 + xy + y2);
2) x3 – y3 = (x – y) (x2 + xy + y2);
3) x3 + y3 = (x + y) (x2 – 2xy + y2); 4) x3 – y3 = (x + y) (x2 – xy + y2)?
750.° Якому з даних виразів тотожно дорівнює многочлен a 3 −27:
1) (a 3) (a 2 6a 9); 3) (a 3) (a 2 3a 9); 2) (a −3) (a 2 −9); 4) (a 3) (a 2 3a 9)?
¿ 751.° Розкладіть на множники:
|
1) a 3 +8; |
5) a 3 +1000; |
9) m 3n 3 +0,001; |
|
2) c3 −64; |
6) 27a 3 −1; |
64 10) m3 − 125 n3. 343 216 |
|
3) 125 −b3; |
7) 1000c3 −216; |
|
|
4) 1 + x 3; |
8) a 3b3 −1; |
|
752.° Розкладіть на множники:
1) x 3 −1; 4) 1 a 3 +b3;
8
2) 27 + a 3; 5) 0,001m3 + 8n3; 3) 216 − y 3; 6) a b3 3 − c3.
753.° Яка з даних рівностей є тотожністю:
1) m 3 8n 6 (m 2n 2) (m 2 2mn 2 4n 4); 2) m 3 8n 6 (m 2n 2) (m 2 2mn 2 4n 4); 3) m 3 8n 6 (m 2n 2) (m 2 2mn 2 4n 4);
4) m 3 8n 6 (m 2n 2) (m 2 2mn 2 4n 4)?
754.° Закінчіть розкладання на множники:
1) 64x6 – 0,027y9 = (4x2)3 – (0,3y3)3 = ...; 2) b12 + 216c15 = (b4)3 + (6c5)3 = ...;
33
![]()
![]()
![]() 1 p18b21p6b7 ....
1 p18b21p6b7 ....
3)
8
755.° Розкладіть на множники:
1) a12 + b9; 4) a24b33 + 1; 7) 0,216 −8c27;
2) x18 – y27; 5) 8m 6 +27n 9; 8) 1000a12b3 +0,001c6d 15.
3) m 6n 3 − p12; 6) 0,027x 21 +0,125y 24;
756.° Подайте у вигляді добутку вираз:
1) a 6 −8; 3) a3 −b15c18; 5) 125c3d 3 +0,008b3;
2) m12 + 27; 4) 1 – a21b9; 6) 64 x 3 − 27 y 6.
729 1000
757.° Знайдіть, використовуючи формулу суми кубів або формулу різниці кубів, значення виразу:
1) 93 + 73 ; 2) 163 −103 .
32 24
758.° Подайте у вигляді многочлена вираз:
1) (x 2) (x 2 2x 4); 3) (a 2 1) (a 4 a 2 1); 2) (2a 1) (4a 2 2a 1); 4) (0,5xy 2) (0,25x 2y 2 xy 4).
759.° Виконайте множення:
1) (b 4) (b2 4b 16); 3) (x 3 6y 2) (x 6 6x 3y 2 36y 4); 2) (2a 3b) (4a 2 6ab 9b2); 4) ![]() a
a ![]() b
b ![]() a 2
a 2 ![]() ab
ab ![]() b2 .
b2 .
760.° Спростіть вираз і знайдіть його значення:
1) (9a 2 3a 1) (3a 1), якщо a = ![]() ;
;
2) (5y 2) (25y 2 10y 4) 8, якщо y ![]() .
.
761.° Знайдіть значення виразу:
1) (1 b2) (1 b2 b4), якщо b = –2; 2) 2x 3 7 (x 1) (x 2 x 1), якщо x = –1.
762.• Розкладіть на множники:
1) (a 6)3 27; 4) 1000 (y 10)3;
2) (2x 1)3 64; 5) (x y)3 (x y)3; 3) 8a 6 −(4a −3)3; 6) (a 2)3 (a 2)3.
763.• Подайте у вигляді добутку вираз:
1) (b 5)3 125; 3) (a b)3 (a b)3; 2) (4 −3x)3 −8x 3; 4) (c 3)3 (c 3)3.
764.• Спростіть вираз:
1) (x 1) (x 2 x 1) (2 x) (4 2x x 2);
2) (x 4) (x 2 4x 16) x (x 5) (x 5);
3) a (a 3)2 (a 3) (a 2 3a 9);
4) (a 1) (a 1) (a 2 a 1) (a 2 a 1) (a 6 1) (a12 1).
765.• Спростіть вираз:
1) (a 5) (a 2 5a 25) (a 1) (a 2 a 1); 2) (y 3) (y 2 3y 9) y (y 3) (y 3) (y 3)2; 3) (a b) (a b) (a 4 a2b2 b4).
766.• Поставте замість зірочок такі одночлени, щоби справджувалася тотожність:
1) (7k p) (* * *) 343k 3 p3;
2) (* *) (25a 4 * 36b2) 125a 6 216b3; 3) (mn *) (* * k 6) m 3n 3 k 9.
767.• Розв’яжіть рівняння:
1) (3x 1) (9x 2 3x 1) 9x (3x 2 4) 17;
2) (x 4) (x 2 4x 16) x (x 7) (x 7) 15; 3) (x 6) (x 2 6x 36) x (x 9)2 4x (4,5x 13,5).
768.• Розв’яжіть рівняння:
1) (7 2x) (49 14x 4x 2) 2x (2x 5) (2x 5) 43; 2) 100 (0,2x 1) (0,04x 2 0,2x 1) 5x (0,16x 2 4).
769.• Доведіть, що значення виразу:
1) 4563 −1563 ділиться націло на 300; 2) 2543 +2383 ділиться націло на 123; 3) 17 6 −1 ділиться націло на 36.
770.• Доведіть, що значення виразу: 1) 3413 +1093 ділиться націло на 90; 2) 215 +33 ділиться націло на 35.
771.•• Укажіть найменше натуральне значення n таке, щоб вираз x2n – y3n можна було розкласти на множники як за формулою різниці квадратів, так і за формулою різниці кубів. Розкладіть отриманий многочлен на множники за цими формулами.
772.•• Придумайте многочлен, який можна розкласти на множники як за формулою різниці квадратів, так і за формулою різниці кубів. Розкладіть придуманий многочлен на множники за цими формулами.
773.•• Чи можна стверджувати, що коли сума двох натуральних чисел ділиться націло на деяке натуральне число, то на це число ділиться націло:
1) різниця їхніх квадратів; 2) сума їхніх квадратів; 3) сума їхніх кубів?
774.•• Доведіть, що сума кубів двох послідовних непарних натуральних чисел ділиться націло на 4.
775.•• Доведіть, що сума кубів двох послідовних натуральних чисел, жодне з яких не кратне 3, ділиться націло на 9.
776.•• Відомо, що числа x і y такі, що х2 + y2 = 1. Знайдіть значення виразу x 6 +3x 2y 2 + y 6.
777.•• Відомо, що числа x і y такі, що х3 – y2 = 2. Знайдіть значення виразу x 9 −6x 3y 2 − y 6.
778.•• Доведіть, що коли 2a – b = 1, то 8a3 – b3 = 6ab + 1.
779.•• Доведіть, що коли a + 3b = 2, то a 3 27b3 8 18ab.
![]()
780. У двох магазинах проводять акції. У магазині «Модний одяг» будь-яка сорочка деякої фірми коштує 600 грн, а при покупці двох сорочок знижка на другу сорочку становить 60 %. У магазині «Сучасний одяг» сорочка тієї самої фірми коштує 550 грн, а при покупці двох сорочок знижка на другу сорочку становить 40 %. У якому магазині вигідніше придбати дві сорочки?
781. На круговій діаграмі (рис. 11) наведено розподіл коштів бю-джету сім’ї Федоренків. Визначте:
1) скільки відсотків бюджету йде на транспортні витрати;
2) на скільки відсотків витрати на оплату квартири та комунальні послуги менші, ніж витрати на відпочинок і розваги;
3) у скільки разів витрати на харчування перевищують витрати на покупку непродовольчих товарів.
²íø³ âèòðàòè Òðàíñïîðòí³ âèòðàòè
![]() Ïîêóïêà íåïðîäîâîëü÷èõÏëàòà çà êâàðòèðó òîâàð³âòà êîìóíàëüí³ ïîñëóãè
Ïîêóïêà íåïðîäîâîëü÷èõÏëàòà çà êâàðòèðó òîâàð³âòà êîìóíàëüí³ ïîñëóãè
24 %12 %
Âèòðàòè íà â³äïî÷èíîêÕàð÷óâàííÿ
³ ðîçâàãè32 %
18 %
Рис. 11
782. В одному ящику було на 12 кг яблук більше, ніж у другому. Коли з першого ящика переклали в другий 4 кг яблук, то виявилося, що маса яблук у другому ящику становить ![]() маси яблук у першому. Скільки кілограмів яблук було в кожному ящику спочатку?
маси яблук у першому. Скільки кілограмів яблук було в кожному ящику спочатку?
783. Якою є остання цифра значення виразу 316 +716 ?
784. Знайдіть значення кожного з даних виразів при a = 1 і a = –1:
1) a + a 2 + a 3 + a 4 +... + a 99 + a100; 3) aa 2a 3a 4...a 99a100; 2) a + a 2 + a 3 + a 4 +... + a 98 + a 99; 4) aa 2a 3a 4...a 98a 99.
![]() ГОТУЄМОСЯ ДО ВИВЧЕННЯ НОВОЇ ТЕМИ
ГОТУЄМОСЯ ДО ВИВЧЕННЯ НОВОЇ ТЕМИ
785. Розкладіть на множники:
1) 3x 2 +12xy; 5) 49b2 −c2;
2) 10m 5 −5m ; 6) p2 +12pk +36k 2;
3) ab – ac + 7b – 7c; 7) 100a 4 − 1 b2;
9
4) 6x xy 6y y 2; 8) 25a 2 −(a −3)2.
|
786. Розв’яжіть рівняння: |
|
|
1) (x – 4) (x + 3) = 0; |
4) 9x 2 6x 1 0; |
|
2) x 2 81 0; |
5) x (x + 7) (3x – 2) = 0; |
|
3) 7x 2 21x 0; |
6) 12x 3 2x 2 0. |
 УЧИМОСЯ РОБИТИ НЕСТАНДАРТНІ КРОКИ
УЧИМОСЯ РОБИТИ НЕСТАНДАРТНІ КРОКИ
787. Є 100 купок монет по 100 монет у кожній. Одна з купок складається з фальшивих монет, кожна з яких на 1 г легша від справжньої. Маса справжньої монети становить 10 г. Яку найменшу кількість зважувань на терезах з електронним табло треба зробити, щоб знайти купку з фальшивих монет?
![]() 19. Застосування різних способів
19. Застосування різних способів
розкладання многочлена на множники
У попередніх пунктах ми розглянули такі способи розкладання многочлена на множники:
• винесення спільного множника за дужки;
• метод групування;
• застосування формул скороченого множення.
Проте в математиці під час розв’язування багатьох задач часто доводиться використовувати кілька прийомів, застосовуючи їх у певній послідовності. Зокрема, є многочлени, для розкладання яких на множники треба застосувати одразу кілька способів.
Виникає природне запитання: які способи та у якій послідовності треба застосовувати при розкладанні многочлена на множники? Універсальних рекомендацій не існує, усе залежить від конкретного многочлена. І все ж дамо кілька загальних порад:
1) якщо це можливо, то розкладання треба починати з винесення спільного множника за дужки;
2) далі потрібно перевірити, чи можна застосувати формули скороченого множення;
3) якщо не вдається застосувати формули скороченого множення, то можна спробувати скористатися методом групування.
![]() ПРИКЛАД 1 Розкладіть на множники многочлен:
ПРИКЛАД 1 Розкладіть на множники многочлен:
1) 3a2b – 12b; 3) 24m4 + 3m;
2) –5x2 + 30xy – 45y2; 4) 3a3 + 21a2 – 6a2b – 42ab.
Розв’язання. 1) Застосувавши послідовно винесення спільного множника за дужки й формулу різниці квадратів, отримаємо:
3a2b – 12b = 3b (a2 – 4) = 3b (a – 2) (a + 2).
2) Застосувавши послідовно винесення спільного множника за дужки й формулу квадрата різниці, отримаємо:
–5x2 + 30xy – 45y2 = –5 (x2 – 6xy + 9y2) = –5 (x – 3y)2.
3) Винесемо спільний множник за дужки та застосуємо формулу суми кубів:
24m4 + 3m = 3m (8m3 + 1) = 3m (2m + 1) (4m2 – 2m + 1).
4) Комбінуючи метод винесення спільного множника за дужки та метод групування, матимемо:
3a3 + 21a2 – 6a2b – 42ab = 3a (a2 + 7a – 2ab – 14b) =
= 3a ((a2 + 7a) + (–2ab – 14b)) = 3a (a (a + 7) – 2b (a + 7)) =
![]() = 3a (a + 7) (a – 2b). ¤
= 3a (a + 7) (a – 2b). ¤
![]() ПРИКЛАД 2 Подайте у вигляді добутку многочленів:
ПРИКЛАД 2 Подайте у вигляді добутку многочленів:
1) x16 – 1; 2) a12 – b12.
Розв’язання. 1) x16 – 1 = (x8 – 1) (x8 + 1) =
= (x4 – 1) (x4 + 1) (x8 + 1) = (x2 – 1) (x2 + 1) (x4 + 1) (x8 + 1) = = (x – 1) (x + 1) (x2 + 1) (x4 + 1) (x8 + 1).
2) a12 – b12 = (a6 – b6) (a6 + b6) = (a3 – b3) (a3 + b3) (a6 + b6).
Ми отримали три множники, один з яких є різницею кубів, а два інших — сумою кубів. Використовуючи відповідні формули, отримуємо:
a12 – b12 = (a – b) (a2 + ab + b2) (a + b) (a2 – ab + b2) ×
![]() × (a2 + b2) (a4 – a2b2 + b4). ¤
× (a2 + b2) (a4 – a2b2 + b4). ¤
![]() ПРИКЛАД 3 Розкладіть на множники:
ПРИКЛАД 3 Розкладіть на множники:
1) m2 – 16n2 + 2m – 8n; 2) x2 + 4xy + 4y2 – 16.
Розв’язання. 1) m2 – 16n2 + 2m – 8n = (m2 – 16n2) + (2m – 8n) = = (m – 4n) (m + 4n) + 2 (m – 4n) = (m – 4n) (m + 4n + 2).
2) x2 + 4xy + 4y2 – 16 = (x2 + 4xy + 4y2) – 16 =
![]() = (x + 2y)2 – 42 = (x + 2y – 4) (x + 2y + 4). ¤
= (x + 2y)2 – 42 = (x + 2y – 4) (x + 2y + 4). ¤
![]() ПРИКЛАД 4 Розв’яжіть рівняння x3 + x2 – 4x – 4 = 0.
ПРИКЛАД 4 Розв’яжіть рівняння x3 + x2 – 4x – 4 = 0.
Розв’язання. Маємо:
x2 (x + 1) – 4 (x + 1) = 0;
(x + 1) (x2 – 4) = 0;
![]() (x + 1) (x – 2) (x + 2) = 0; x + 1 = 0, або x – 2 = 0, або x + 2 = 0; x = –1, або x = 2, або x = –2. Відповідь: –1; 2; –2. ¤
(x + 1) (x – 2) (x + 2) = 0; x + 1 = 0, або x – 2 = 0, або x + 2 = 0; x = –1, або x = 2, або x = –2. Відповідь: –1; 2; –2. ¤
![]() ПРИКЛАД 5 Розкладіть на множники тричлен x2 + 8x – 9, виділивши попередньо квадрат двочлена.
ПРИКЛАД 5 Розкладіть на множники тричлен x2 + 8x – 9, виділивши попередньо квадрат двочлена.
Розв’язання. Якщо до суми x2 + 8x додати число 16, то отриманий вираз x2 + 8x + 16 можна «згорнути» за формулою квадрата суми. Тому, додавши до даного тричлена число 16 і віднявши від нього 16, отримуємо:
![]() x2 + 8x – 9 = x2 + 8x + 16 – 16 – 9 = (x + 4)2 – 25 = = (x + 4 – 5) (x + 4 + 5) = (x – 1) (x + 9). ¤
x2 + 8x – 9 = x2 + 8x + 16 – 16 – 9 = (x + 4)2 – 25 = = (x + 4 – 5) (x + 4 + 5) = (x – 1) (x + 9). ¤
|
Розв’язання. Оскільки x4 = (x2)2, 4y4 = (2y2)2, то, додавши до даного многочлена 4x2y2 (подвоєний добуток одночленів x2 і 2y2) і віднявши від нього такий самий одночлен, отримуємо: x4 + 4y4 = x4 + 4x2y2 + 4y4 – 4x2y2 = (x2 + 2y2)2 – 4x2y2 =
|
![]()
788.° Закінчіть розкладання на множники:
1) 7a2 – 7b2 = 7 (a2 – b2) = ...;
2) 3y3 – 27y = 3y (y2 – 9) = ...;
3) m5 – m3 = m3 (m2 – 1) = ...;
![]() 49 x y z2 3 6 0 04, yz 8 yz 6x y2 2 0 04, z2 ... .
49 x y z2 3 6 0 04, yz 8 yz 6x y2 2 0 04, z2 ... .
4)
64
789.° Розкладіть на множники многочлен:
1) 2a 2 −2b2; 4) 3ab2 −27a; 7) x 4 −x 2;
2) cx 2 −cy 2; 5) x 3 −4x ; 8) 0,09t 4 −t 6; 3) 3x 2 −3; 6) 2y 3 −18y; 9) ![]() a 2b4c5 −b2c3.
a 2b4c5 −b2c3.
790.° Подайте у вигляді добутку многочлен:
1) 12b2 −12c2; 4) 3mn 2 −48m;
2) 2a2c −2b2c; 5) 7y 3 −7y; 3) 5a 2 −20; 6) a 3 −a 5.
791.° Закінчіть розкладання на множники:
1) 9a2b2 – 6ab2 + b2 = b2 (9a2 – 6a + 1) = ...;
2) 4b2c – 20abc + 25a2c = c (4b2 – 20ab + 25a2) = ...;
3) –3m3 + 6m2n – 3mn2 = –3m (m2 – 2mn + n2) = ... .
|
792.° Розкладіть на множники: |
|
|
1) 3a 2 +6ab+3b2; |
4) −7b2 −14bc −7c2; |
|
2) 5m 2 5n 2 10mn; |
5) x 2y +14xy 2 +49y 3; |
|
3) 3x 2 12x 12; 793.° Розкладіть на множники: |
6) 8a 3b 56a2b2 98ab3. |
|
1) 8x 2 +16xy +8y 2; |
3) −12b3 −12b2 −3b; |
|
2) 2a 2 24ab 72b2; |
4) 48m3n – 72m2n + 27mn. |
794.° Закінчіть розкладання на множники:
1) a4 – 10 000 = (a2)2 – 1002 = (a2 – 100) (a2 + 100) = ...; 2) m8 – n4 = (m4)2 – (n2)2 = (m4 – n2) (m4 + n2) = ... .
795.° Подайте у вигляді добутку многочлен:
1) a 4 −b4; 2) c4 −81.
796.° Розкладіть на множники:
1) x 4 −16; 2) y 8 −1.
797.° Закінчіть розкладання на множники:
1) 16x – 2x4 = 2x (8 – x3) = ...; 2) 3a5 + 375a2 = 3a2 (a3 + 125) = ... .
798.° Розкладіть на множники:
1) 4a 3 −4b3; 4) –x4 + 27x; 2) 2m 3 −16; 5) 2a 4 −250a; 3) 7 +7b3; 6) 9a 5 −9a 2.
799.° Подайте у вигляді добутку многочлен:
1) 3x3 + 3y3; 2) 5m 4 −320mn 3; 3) 6c5 −6c8.
800.• Розкладіть на множники:
1) a7 + ab6; 2) x 8 − y 8; 3) c6 −1.
801.• Розкладіть на множники:
1) c6 + c9; 2) m 9 −n 9; 3) a 8 −b4.
802.• Подайте у вигляді добутку многочлен:
|
1) 3ab + 15b – 3a – 15; |
5) a 3 |
a 2 a 1; |
|
|
2) 84 – 42y – 7xy + 14x; |
6) 2x 3 |
2xy 2 8x 2 |
8y 2; |
|
3) abc + 6ac + 8ab + 48a; |
7) 5a 2 |
5b2 15a 3b |
15ab3; |
|
4) m 3 m 2n m 2 mn; |
8) a2b2 |
1 b2 a 2. |
|
803.• Розкладіть на множники:
1) 15cx + 2cy – cxy – 30c;
2) 35a2 – 42ab + 10a2b – 12ab2;
3) x 3 + x 2y + x 2 + xy;
4) mn 4 n 4 mn 3 n 3.
804.• Розкладіть на множники:
1) (a 2 b2)2 4a 2b2; 5) 9a 2 c2 6ac 9; 2) 81 (x 2 6x)2; 6) a 2 −b2 −10b−25; 3) a 2 2ab b2 c2; 7) 49 y 2 x 2 14x ; 4) c2 4c 4 k 2; 8) mn 2 −m 3 −12m 2 −36m.
805.• Подайте у вигляді добутку вираз:
1) (m 2 −2m)2 −1; 4) 64x2 + 48xy + 9y2 – 144; 2) 16 (m 2 4m)2; 5) c2 a 2 22a 121;
3) x 2 18xy 81y 2 z 2; 6) 100 −25y 2 −60x 2y −36x 4.
806.• Розкладіть на множники:
1) a 2 −b2 −a −b; 6) a 2 10a 25 ab 5b;
2) x y x 2 y 2; 7) 8mp 8np m 2 2mn n 2;
3) 4m 2 9n 2 2m 3n; 8) a 3 b3 a 2b ab2;
4) c2 d 2 4c 4d; 9) m 3 8n 3 m 2 4mn 4n 2; 5) 5x 2y 5xy 2 x 2 y 2; 10) a 3 4a 2 4a 1.
807.• Розкладіть на множники:
1) m 2 n 2 m n; 5) 49c2 14c 1 21ac 3a;
2) c d c2 d 2; 6) ax 2 + ay 2 + x 4 +2x 2y 2 + y 4; 3) 16x 2 −25y 2 −4x −5y; 7) 27c3 d 3 9c2 3cd d 2; 4) 12a 2b3 3a 3b2 16b2 a 2; 8) b3 2b2 2b 1.
808.• Розкладіть на множники:
1) x 2 (x 2) 18x (x 2) 81 (x 2);
2) 4x (y 2 9) 4x 2 (y 2 9) 9 y 2;
3) b2 (a 1) a2 (b 1);
4) (a −b) (b2 −c2) −(b−c) (a2 −b2).
809.• Подайте у вигляді добутку вираз:
1) x 2 (x 4) 20x (x 4) 100 (x 4);
2) a 2 −36 −2a (36 −a 2) −a 2 (36 −a 2); 3) a 2 (b−1) −b2 (a −1);
4) (m −n) (n 3 − p3) −(n − p) (m 3 −n 3).
810.• Розв’яжіть рівняння:
1) x 3 4x 0; 5) x 3 10x 2 25x 0;
2) x 4 x 2 0; 6) x3 + 2x2 – 9x – 18 = 0;
3) x5 – 36x3 = 0; 7) x 3 5x 2 4x 20 0;
4) 9x 3 x 0; 8) x 5 x 4 x 1 0.
811.• Розв’яжіть рівняння:
1) x 3 x 0; 4) 49x 3 14x 2 x 0; 2) x 4 x 2 0; 5) x 3 x 2 x 1 0; 3) x 4 8x 3 0; 6) x 3 4x 2 25x 100 0.
812.• Чи є тотожністю рівність:
1) (a 1)3 9 (a 1) (a 1) (a 4) (a 2); 2) (x 2 1)2 4x 2 (x 1)2 (x 1)2 ?
813.• Доведіть тотожність:
1) (a 2)3 25 (a 2) (a 2) (a 7) (a 3);
2) a2 + 2ab + b2 – c2 + 2cd – d2 = (a + b + c – d) (a + b – c + d).
814.• Розкладіть вираз на множники двома способами:
а) застосуйте формулу різниці квадратів;
б) розкрийте дужки та застосуйте метод групування:
1) (ab 1)2 (a b)2; 2) (a 2b)2 (ab 2)2.
815.•• Подайте у вигляді куба двочлена вираз:
1) a 3 +3a 2 +3a +1; 2) b3 6b2 12b 8.
816.•• Доведіть тотожність:
1) (a b c)3 a 3 b3 c3 3 (a b) (b c) (a c); 2) (a b)3 (b c)3 (a c)3 3 (a b) (b c) (a c).
817.•• Розкладіть на множники вираз:
1) (x – y) (x + y) + 2 (x + 3y) – 8; 2) (2a – 3b) (2a + 3b) – 4 (a + 3b) – 3.
818.•• Подайте у вигляді добутку вираз:
1) (5x – y2) (5x + y2) – 2 (15x – 7y2) – 40;
2) (3m 2n) (12m 5n) 3m (3n 4) 2 (3n 2 20n 12).
819.•• Розкладіть на множники тричлен, виділивши попередньо квадрат двочлена:
1) x 2 10x 24; 4) 4a 2 12a 5; 2) a 2 4a 32; 5) 9x 2 24xy 7y 2; 3) b2 −3b −4; 6) 36m 2 60mn 21n 2.
820.•• Розкладіть на множники многочлен:
1) x 2 4x 3; 4) x 2 x 6;
2) a 2 2a 24; 5) c2 +8cd +15d 2; 3) y 2 +12y +35; 6) 9x 2 30xy 16y 2.
821.•• Значення змінних x1 і x2 є такими, що виконуються рівності x 1 x 2 8, x 1x 2 =5. Знайдіть значення виразу:
1) x 1x 22 −x 12x 2; 2) x 12 + x 22; 3) (x 1 + x 2)2; 4) x 13 −x 23.
822.•• Значення змінних x і y є такими, що виконуються рівності x + y = 6, xy = –3. Знайдіть значення виразу:
1) x 3y 2 + x 2y 3; 2) (x − y)2; 3) x 4 + y 4.
823.* Доведіть, що при будь-якому натуральному n значення виразу (2n 1)3 4n 2 2n 1 ділиться націло на 16.
824.* Розкладіть на множники:
1) x 4 5x 2 4; 3) 4x 4 12x 2 1; 5) x 4 +4; 2) x 4 + x 2 +1; 4) x 5 + x +1; 6) x 8 x 4 2.
825.* Подайте у вигляді добутку вираз:
1) x4 + 5x2 + 9; 2) x 4 8x 2 4.
826.* Доведіть, що при будь-якому натуральному значенні n, відмінному від 1, значення виразу n 4 +n 2 +1 є складеним числом.
![]()
827. У магазині є відділ книг і відділ канцтоварів. На діаграмі (рис. 12) наведено дані про виручку магазину за відділами за тиждень (у понеділок магазин не працює).
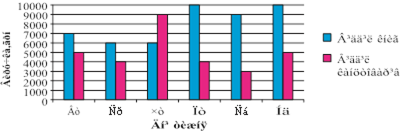
Рис. 12
1) У який день тижня виручка відділу книг була найбільшою?
2) У який день тижня виручка відділу канцтоварів була найменшою? На скільки гривень у цей день виручка відділу канцтоварів була меншою від виручки відділу книг?
3) Чи був такий день тижня, коли виручка відділу канцтоварів була більшою за виручку відділу книг? У разі ствердної відповіді знайдіть, на скільки відсотків у цей день виручка відділу канцтоварів була більшою за виручку відділу книг.
4) Скільки в середньому становила в день протягом цього тижня виручка:
а) відділу книг; б) усього магазину?
828. Під час оплати послуг через платіжний термінал стягується комісія в розмірі 3 %. Термінал приймає суми, кратні 10 грн. Івась хоче поповнити рахунок свого мобільного телефону не менше ніж на 200 грн. Яку найменшу суму грошей він має заплатити через цей термінал?
829. Дано три числа, з яких кожне наступне на 4 більше за попереднє. Знайдіть ці числа, якщо добуток меншого й більшого з них на 88 менший від добутку більшого й середнього.
830. Петро спочатку піднявся на гору зі швидкістю 2,5 км/год, а потім спустився іншою дорогою зі швидкістю 4 км/год. Знайдіть загальний шлях, пройдений Петром, якщо дорога на гору на 3 км коротша від дороги з гори, а час, витрачений на весь шлях, становить 4 год.
831. Розв’яжіть рівняння:
1) | 7x – 3 | = 4; 3) 4 (x – 2) + 5 | x | = 10; 2) | | x | – 10 | = 8; 4) | x | = 3x – 8.
832. Доведіть, що сума трицифрового числа та подвоєної суми його цифр ділиться націло на 3.
![]() ГОТУЄМОСЯ ДО ВИВЧЕННЯ НОВОЇ ТЕМИ
ГОТУЄМОСЯ ДО ВИВЧЕННЯ НОВОЇ ТЕМИ
833. Обчисліть значення y за формулою y = 0,2x – 3, якщо: 1) x = 4;
2) x = –3.
834. Знайдіть координати точок A, B, C, D, E, F, K, M, N, зображених на рисунку 13.

завдання № 5 «Перевірте себе» в тестовій формі
![]()
835. На координатній площині позначте точки: A (2; 3), B (4; 5), C (–3; 7), D (–2; 2), K (–2; –2), M (0; 2), N (–3; 0), P (1; –6), F (–4; –2).
836. Побудуйте відрізки AB і CD та знайдіть координати точки перетину цих відрізків, якщо A (–5; –2), B (1; 4), C (–3; 2), D (2; –3).
837. Як розміщена на координатній площині відносно осі x точка: 1) A (2; 6); 2) B (–3; 1); 3) C (–4; –5); 4) D (–3; 0)?
838. Знайдіть координати вершин квадрата зі стороною 4, якщо дві його сторони лежать на осях координат, а добуток координат однієї з вершин — додатне число. Скільки розв’язків має задача? Поновіть у пам’яті зміст пп. 26, 34 на с. 272, 274, 275.
 УЧИМОСЯ РОБИТИ НЕСТАНДАРТНІ КРОКИ
УЧИМОСЯ РОБИТИ НЕСТАНДАРТНІ КРОКИ
839. Нехай x1, x2, ..., x25 — деякий набір натуральних чисел, а набір y1, y2, ..., y25 отримано з нього в результаті перестановки деяких чисел. Доведіть, що значення виразу (x1 – y1) × × (x2 – y2) ... (x25 – y25) є парним числом.
ЗАВДАННЯ № 5 «ПЕРЕВІРТЕ СЕБЕ» В ТЕСТОВІЙ ФОРМІ
1. Подайте у вигляді многочлена вираз (x – 6) (x2 + 6x + 36).
А) x3 – 36; Б) x3 + 36; В) x3 – 216; Г) x3 + 216.
2. Знайдіть многочлен M, якщо y3 – 64 = (y – 4)æM.
А) y2 – 8y + 16; В) y2 – 4y + 16; Б) y2 + 8y + 16; Г) y2 + 4y + 16.
3. Спростіть вираз (a2 + 2b3) (a4 – 2a2b3 + 4b6).
А) a6 + 4b9; Б) a6 – 4b9; В) a6 – 8b9; Г) a6 + 8b9.
4. Розкладіть на множники многочлен 3c2 – 48.
А) 3 (c – 16); В) 3 (c – 4)2;
Б) 3 (c – 4) (c + 4); Г) 3c (c – 16).
5. Розкладіть на множники вираз 7a2 – 42a + 63.
А) 7 (a – 3) (a + 3); В) 7 (a + 3)2;
Б) 7 (a – 3)2; Г) 7 (a – 9)2.
6. Розкладіть на множники многочлен a8 – a6.
А) a6 (a – 1); В) a6 (a + 1)2;
Б) a6 (a – 1) (a + 1); Г) a6 (a – 1)2.
7. Розкладіть на множники вираз m2 – n2 + m + n.
А) (m + n) (m – n + 1); В) (m – n) (m + n + 1); Б) (m – n) (m – n + 1); Г) (m + n) (m + n + 1).
8. Подайте у вигляді добутку вираз x2 – y2 + 14y – 49.
А) (x – y + 7) (x + y + 7);
Б) (x – y – 7) (x + y + 7); В) (x – y + 7) (x + y – 7);
Г) (x – y – 7) (x + y – 7).
9. Розкладіть на множники многочлен 81a4 – 1.
А) (3a – 1) (3a + 1) (9a2 + 1);
Б) (3a2 – 1) (3a2 + 1) (9a2 + 1);
В) (3a – 1)2 (3a + 1)2;
Г) (3a – 1)4.
10. Розв’яжіть рівняння 49x – x2 = 0.
А) 0; 7; В) 0; 49;
Б) –7; 0; 7; Г) –7; 7.
11. Розв’яжіть рівняння x3 + 3x2 – x – 3 = 0.
А) –1; 1; В) 1; 3;
Б) –1; 3; Г) –3; –1; 1.
12. Подайте у вигляді добутку вираз (x2 – 2)2 – 4 (x2 – 2) + 4.
А) (x – 4)2; В) x4;
Б) (x – 2)2 (x + 2)2; Г) (x2 – 6)2.
![]()
Тут трьома східними мовами — арабською, китайською та івритом — записано добре відому вам властивість: від перестановки місць доданків сума не змінюється.

Проте людина, яка не володіє цими мовами, такого простого речення не зрозуміє. Тоді на допомогу приходить інтернаціональна математична мова. Переклад нею має такий вигляд: a + b = b + a.
Як і будь-яка інша мова, вона має свій алфавіт — математичні символи. Це цифри, букви, знаки математичних дій тощо. З них складають «слова» математичної мови, наприклад вирази. Зі слів складають «речення» математичної мови, наприклад формули й т. ін.
мова, зрозуміла всім
![]()
Здавалося б, що може бути простішим — використати математичну фразу «2x = 4» для запису лінійного рівняння. Однак навіть великий аль-Хорезмі[5] записував це речення громіздко: «Два корені дорівнюють 4 дирхемам[6]». Це пов’язано з тим, що за часів аль-Хорезмі математичної символіки ще не існувало.
Сказане зовсім не означає, що до ІХ ст. вчені не робили спроб створити математичну мову.
Ще в І ст. грецький математик Герон Александрійський почав позначати невідому величину буквою V («сигма»). Наступний крок у створенні символіки зробив у ІІІ ст. Діофант Александрійський. У своїй знаменитій праці «Арифметика» він запровадив позначення не лише для невідомої величини, але й для деяких її степенів: перший степінь — s;
другий степінь — Dn (від DunamiV — «дюнаміс», що означає
«сила», «степінь»);
третій степінь — Kn (від KuboV — «кубос», тобто «куб»).
Для рівності Діофант застосовував знак is — перші дві букви слова isoV — «ісос», тобто «рівний».
Навряд чи символіку Діофанта можна вважати зручною та наочною. Наприклад, він не запровадив ніяких спеціальних символів для позначення дій додавання та множення. Позначення всіх невідомих величин однією буквою V також значною мірою ускладнювало запис розв’язання задач, у яких фігурувало кілька змінних. Із занепадом епохи античності алгебраїчну символіку Діофанта практично було забуто.
![]() Відновлення процесу створення алгебраїчної символіки пов’язане з роботами талановитого німецького вченого ХІІІ ст. Йордана Неморарія, який відродив у європейській математиці ідею буквеної символіки.
Відновлення процесу створення алгебраїчної символіки пов’язане з роботами талановитого німецького вченого ХІІІ ст. Йордана Неморарія, який відродив у європейській математиці ідею буквеної символіки.
У ХV ст. широкого розповсюдження набули символи, які застосовував видатний італійський математик Лука Паччолі.
Чимало зробили для вдосконалення математичної мови німецькі математики ХVІ ст.
Ян Відман і Адам Різе.
Засновником буквеної символіки по праву вважають найвидатнішого французько- Франсуа Вієт го математика ХVІ ст. Франсуа Вієта. Він (1540–1603) перший позначив буквами не тільки невідомі, але й дані величини. Вієт запропонував: «Шукані величини будемо позначати буквою A або іншою голосною (E, I, O, U), а дані — буквами B, D, G та іншими приголосними». Такі позначення дали змогу Вієту не тільки розв’язувати окремі рівняння, але й досліджувати процес розв’язування цілого класу рівнянь. Наприклад, завдяки символіці Вієта всі лінійні рівняння можна записати у вигляді ax = b, а отже, побудувати процес розв’язування рівняння в загальному вигляді так, як ми це зробили в п. 2.
Мови багатьох народів продовжують розвиватися. Не є винятком і математична мова. Нові відкриття приносять у математику нові символи й терміни.
Великий внесок у розвиток і систематизацію української математичної термінології зробив професор фізико-математичного факультету Львівського університету Володимир Йосипович Левицький. Його науково-методичні праці значною мірою сприяли становленню й розвитку української математичної школи.
Фундатором української математичної культури по праву вважають ученого з європейським іменем, доктора філософії, професора Мирона Онуфрійовича Зарицького. Його наукові праці та педагогічні здобутки добре відомі в багатьох країнах світу.


|
В. Й. Левицький (1872–1956) |
М. О. Зарицький (1889–1961) |
Головне в параграфі 2
![]()
ГОЛОВНЕ В ПАРАГРАФІ 2
Тотожно рівні вирази
Вирази, відповідні значення яких є рівними при будь-яких значеннях змінних, що входять до них, називають тотожно рівними.
Тотожність
Рівність, яка є правильною при будь-яких значеннях змінних, що входять до неї, називають тотожністю. Прийоми доведення тотожностей
¤ Тотожно перетворюють одну із частин даної рівності, отримуючи іншу частину;
¤ ![]() тотожно перетворюють кожну із частин даної рівності, отримуючи один і той самий вираз;
тотожно перетворюють кожну із частин даної рівності, отримуючи один і той самий вираз;
¤ показують, що різниця лівої та правої частин даної рівності тотожно дорівнює нулю.
Степінь з натуральним показником
Степенем числа a з натуральним показником n, більшим за 1, називають добуток n множників, кожний з яких дорівнює a.
Степенем числа a з показником 1 називають саме це число.
Знак степеня
Підносячи невід’ємне число до степеня, отримуємо невід’ємне число.
Підносячи від’ємне число до степеня з парним показником, отримуємо додатне число, а підносячи від’ємне число до степеня з непарним показником, отримуємо від’ємне число.
Властивості степеня з натуральним показником aman = am + n (основна властивість степеня) am : an = am – n (am)n = amn
(ab)n = anbn
Одночлен
Вираз, який являє собою добуток чисел, змінних та їхніх степенів, називають одночленом.
Одночлен стандартного вигляду
Одночленом стандартного вигляду називають одночлен, що містить тільки один числовий множник, відмінний від нуля, який стоїть на першому місці; решта його множників є степенями з різними основами.
Коефіцієнт одночлена
Числовий множник одночлена, записаного в стандартному вигляді, називають коефіцієнтом одночлена.
Степінь одночлена
Степенем одночлена називають суму показників степенів усіх змінних, що входять до нього. Степінь одночлена, який є числом, відмінним від нуля, вважають рівним нулю.
Многочлен
Вираз, який є сумою кількох одночленів, називають многочленом.
Многочлен стандартного вигляду
Многочлен, складений з одночленів стандартного вигляду, серед яких немає подібних, називають многочленом стандартного вигляду.
Степінь многочлена
Степенем многочлена стандартного вигляду називають найбільший зі степенів одночленів, з яких цей многочлен складений.
Множення одночлена на многочлен
Щоби помножити одночлен на многочлен, потрібно помножити цей одночлен на кожний член многочлена й отримані добутки
додати.
Множення многочленів
Щоби помножити многочлен на многочлен, можна кожний член одного многочлена помножити на кожний член другого й отримані добутки додати.
Добуток різниці та суми двох виразів
(a – b) (a + b) = a2 – b2
Різниця квадратів двох виразів a2 – b2 = (a – b) (a + b)
Квадрат суми двох виразів
(a + b)2 = a2 + 2ab + b2
Квадрат різниці двох виразів
(a – b)2 = a2 – 2ab + b2
Сума кубів двох виразів a3 + b3 = (a + b) (a2 – ab + b2)
Різниця кубів двох виразів a3 – b3 = (a – b) (a2 + ab + b2)

Учитель пише на дошці. При цьому змінюється довжина сліду крейди, маса, об’єм і навіть температура шматочка крейди.
Працює шкільна їдальня. Протягом дня змінюються кількість учнів і учениць, що її відвідали, витрати електроенергії та води, грошова виручка тощо.
Узагалі, у процесах, що відбуваються навколо нас, багато величин змінюють свої значення. Деякі із цих величин пов’язані між собою, тобто зміна однієї величини спричиняє зміну другої.
Багато наук, такі як фізика, хімія, біологія та інші, досліджують залежності між величинами. Вивчає ці зв’язки й математика, будуючи математичні моделі реальних процесів. З поняттям математичної моделі ви вже ознайомилися в п. 3.
Розглянемо кілька прикладів.
![]() ПРИКЛАД 1 Змінюється сторона квадрата. Зрозуміло, що при цьому змінюватиметься також його периметр. Якщо довжину сторони квадрата позначити a, а периметр — P, то залежність значення змінної P від значення змінної a (коротко говорять: «залежність
ПРИКЛАД 1 Змінюється сторона квадрата. Зрозуміло, що при цьому змінюватиметься також його периметр. Якщо довжину сторони квадрата позначити a, а периметр — P, то залежність значення змінної P від значення змінної a (коротко говорять: «залежність
змінної Р від змінної а») можна задати формулою Р = 4а.
Ця формула є математичною моделлю зв’язку між такими величинами, як довжина сторони квадрата та його периметр.
За допомогою цієї формули можна, вибравши довільну довжину сторони, знайти відповідне значення периметра квадрата. Тому в цій моделі змінну a називають незалежною змінною, а змінну P — залежною змінною.
![]() Наголосимо, що ця формула задає правило, за допомогою якого за значенням незалежної змінної можна однозначно знайти значення залежної змінної.
Наголосимо, що ця формула задає правило, за допомогою якого за значенням незалежної змінної можна однозначно знайти значення залежної змінної. ¤
ФУНКЦІЇ
![]() ПРИКЛАД 2 ѳì’ÿ ïîêëàëà â áàíê 10 000 ãðí ï³ä 10 % ð³÷íèõ. Òîä³ ÷åðåç ð³ê âåëè÷èíà M — ñóìà ãðîøåé íà ðàõóíêó ñòàíîâèòèìå
ПРИКЛАД 2 ѳì’ÿ ïîêëàëà â áàíê 10 000 ãðí ï³ä 10 % ð³÷íèõ. Òîä³ ÷åðåç ð³ê âåëè÷èíà M — ñóìà ãðîøåé íà ðàõóíêó ñòàíîâèòèìå
M ![]() 10000
10000![]()
![]()
![]() 11000 (ãðí).
11000 (ãðí).
×åðåç äâà ðîêè öÿ ñóìà ñêëàäàòèìå
M ![]() 11000
11000![]()
![]()
![]() 12100 (ãðí).
12100 (ãðí).
Àíàëîã³÷íî ìîæíà âñòàíîâèòè, ùî ÷åðåç òðè ðîêè M = 13 310 ãðí, ÷åðåç ÷îòèðè ðîêè M = 14 641 ãðí, ÷åðåç ï’ÿòü ðîê³â M = 16 105,1 ãðí.
Ó òàáëèö³ ïîêàçàíî, ÿê çàëåæèòü ñóìà ãðîøåé íà ðàõóíêó â³ä ê³ëüêîñò³ ðîê³â, ÿê³ ìèíóëè ç ìîìåíòó â³äêðèòòÿ ðàõóíêó.
|
ʳëüê³ñòü ðîê³â n |
1 |
2 |
3 |
4 |
5 |
|
Ñóìà ãðîøåé íà ðàõóíêó M, ãðí |
11 000 |
12 100 |
13 310 |
14 641 |
16 105,1 |
Öÿ òàáëèöÿ º ìàòåìàòè÷íîþ ìîäåëëþ çàëåæíîñò³ âåëè÷èíè M â³ä âåëè÷èíè n. Òóò n âèñòóïຠâ ðîë³ íåçàëåæíî¿ çì³ííî¿, à M — çàëåæíî¿.
![]() Íàãîëîñèìî, ùî öÿ òàáëèöÿ çàäຠïðàâèëî, çà äîïîìîãîþ ÿêîãî çà çíà÷åííÿì íåçàëåæíî¿ çì³ííî¿ ìîæíà îäíîçíà÷íî çíàéòè çíà÷åííÿ çàëåæíî¿ çì³ííî¿.
Íàãîëîñèìî, ùî öÿ òàáëèöÿ çàäຠïðàâèëî, çà äîïîìîãîþ ÿêîãî çà çíà÷åííÿì íåçàëåæíî¿ çì³ííî¿ ìîæíà îäíîçíà÷íî çíàéòè çíà÷åííÿ çàëåæíî¿ çì³ííî¿. ¤
![]() ПРИКЛАД 3 Íà ðèñóíêó 14 çîáðàæåíî ãðàô³ê çàëåæíîñò³ òåìïåðàòóðè ïîâ³òðÿ â³ä ÷àñó äîáè.
ПРИКЛАД 3 Íà ðèñóíêó 14 çîáðàæåíî ãðàô³ê çàëåæíîñò³ òåìïåðàòóðè ïîâ³òðÿ â³ä ÷àñó äîáè.
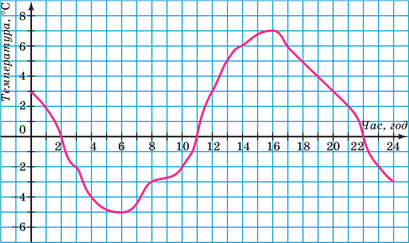
Ðèñ. 14
За цим графіком можна, вибравши довільний момент часу t, знайти відповідну температуру повітря T (у градусах Цельсія). Таким чином, величина t є незалежною змінною, а величина T — залежною.
Цей графік можна розглядати як математичну модель залежності величини T (температури) від величини t (часу).
![]() Наголосимо, що даний графік задає правило, за допомогою якого за значенням незалежної змінної можна однозначно знайти значення залежної змінної.
Наголосимо, що даний графік задає правило, за допомогою якого за значенням незалежної змінної можна однозначно знайти значення залежної змінної. ¤
Незважаючи на істотні відмінності моделей залежностей, описаних у цих трьох прикладах, їм усім притаманне таке: указано правило, за допомогою якого за кожним значенням незалежної змінної можна знайти єдине значення залежної змінної. Таке правило називають функцією, а відповідну залежність однієї змінної від другої — функціональною.
Отже, правила, описані в прикладах 1, 2 і 3, є функціями.
Не кожна залежність однієї змінної величини від другої є функціональною. Наприклад, нехай довжина маршруту автобуса дорівнює 15 км. Вартість проїзду визначається за такою таблицею:
|
Вартість проїзду, грн |
12 |
14 |
16 |
|
Довжина шляху, який проїжджає пасажир, км |
до 5 |
від 5 до 10 |
від 10 до 15 |
Зрозуміло, що змінні величини «вартість проїзду» й «довжина шляху, який проїжджає пасажир» пов’язані між собою. Проте якщо вважати вартість проїзду незалежною змінною, то описана залежність не є функціональною. Справді, якщо пасажир заплатив 12 грн, то не можна однозначно встановити довжину шляху, який він проїхав.
Якщо в прикладі 3 температуру T вважати незалежною змінною, то не завжди можна за значенням величини T однозначно знайти значення величини t. Тому наведена залежність часу t від температури T не є функціональною.
Зазвичай незалежну змінну позначають буквою x, залежну — буквою y, функцію (правило) — буквою f. Якщо змінна y функціонально залежить від змінної x, то цей факт позначають так: y = f (x) (читають: «ігрек дорівнює еф від ікс»).
Незалежну змінну ще називають аргументом функції.
Усі значення, яких набуває аргумент, утворюють область визначення функції. Так, у прикладі 1 областю визначення функції
є всі додатні числа; у прикладі 2 — натуральні числа 1, 2, 3, 4, 5; у прикладі 3 — усі невід’ємні числа, що не перевищують 24.
Для функції f кожному значенню аргументу x відповідає деяке значення залежної змінної y. Значення залежної змінної ще називають значенням функції. Значення функції f, яке відповідає значенню x0 аргументу x, позначають f (x0). Наприклад, f (7) — це значення функції при x =7.
Так, якщо кожне з правил, описаних у прикладах 1, 2 і 3, позначити буквою f, то в першому прикладі f (2) = 8, у другому f (2) = 12 100, у третьому f (2) = 0. Узагалі, запис f (a) = b означає, що значенню a аргументу відповідає значення b функції.
Усі значення, яких набуває залежна змінна, утворюють область значень функції.
У прикладі 1 область значень функції — це всі додатні числа; у прикладі 2 — числа, записані в другому рядку таблиці; у прикладі 3 — усі числа, не менші від −5 й не більші за 7.

840.° Чи пов’язані між собою периметр рівностороннього трикутника та його сторона? Якщо сторона трикутника дорівнює a, а периметр — P, то якою формулою можна задати залежність змінної P від змінної a? Чи є ця залежність функціональною?
841.° Чи пов’язані між собою площа квадрата та його сторона? Якщо сторона квадрата дорівнює a, а площа — S, то якою формулою можна задати залежність змінної S від змінної a? Чи є ця залежність функціональною?
842.° Автомобіль рухається зі швидкістю 60 км/год. Як залежить довжина пройденого ним шляху s від часу руху t? Задайте цю залежність формулою. Чи є ця залежність функціональною? У разі ствердної відповіді назвіть аргумент відповідної функції.
¿ 843.° У цистерні було 300 л води. Через відкритий кран щохвилини із цистерни виливається 2 л води. Задайте формулою залежність об’єму V води в цистерні від часу t, протягом якого з неї виливається вода. Чи є правило, за допомогою якого за значенням змінної t можна знайти значення змінної V, функцією? У разі ствердної відповіді вкажіть область визначення та область значень цієї функції.
844.° Нехай a — довжина ребра куба, V — його об’єм. Задайте формулою залежність змінної V від змінної a. Чи є ця залежність функціональною?
845.° Автомобіль проїхав 120 км зі швидкістю v. Якою формулою можна задати залежність часу t, витраченого на поїздку, від швидкості v автомобіля? Чи є ця залежність функціональною? У разі ствердної відповіді вкажіть, яка зі змінних є аргументом відповідної функції.
846.° Нехай градусні міри двох суміжних кутів дорівнюють a і b. Задайте формулою залежність b від a. Чи є ця залежність функціональною? У разі ствердної відповіді вкажіть, яка зі змінних є аргу ментом відповідної функції, її область визначення та область значень.
847.° У вашому класі було проведено контрольну роботу з математики.
1) Кожному учню поставили у відповідність оцінку, яку він отримав.
2) Кожній оцінці поставили у відповідність учня, який її отримав.
Яке із цих правил є функцією?
848.° Розглянемо правило, згідно з яким кожному натуральному числу відповідає протилежне йому число. Чи є таке правило функцією?
849.° Кожному невід’ємному числу поставили у відповідність саме це число, а кожному від’ємному числу — число, йому протилежне. Чи є таке правило функцією?
850.° Кожному раціональному числу, відмінному від нуля, відповідає обернене до нього число. Чи є таке правило функцією?
851.° Користуючись графіком залежності температури повітря від часу протягом доби (рис. 14), визначте:
1) якою була температура повітря о 4 год; о 6 год; о 10 год; о 18 год; о 22 год;
2) о котрій годині температура повітря була 5 °С; –2 °С;
3) о котрій годині температура повітря дорівнювала нулю;
4) якою була найнижча температура та о котрій годині;
5) якою була найвища температура та о котрій годині;
6) протягом якого проміжку часу температура повітря була нижчою від 0 °С; вищою за 0 °С;
7) протягом якого проміжку часу температура повітря підвищувалася; знижувалася.
Складіть за графіком таблицю зміни температури повітря протягом доби через кожні 2 год.
852.° На рисунку 15 зображено графік зміни температури розчину під час хімічного досліду.
1) Якою була початкова температура розчину?
2) Якою була температура розчину через 30 хв після початку досліду; через півтори години?
3) Якою була найвища температура розчину та через скільки хвилин після початку досліду?
4) Через скільки хвилин після початку досліду температура розчину була 35 °С?
Складіть за графіком таблицю зміни температури розчину через кожні 10 хв протягом перших двох годин після початку досліду.
853.° На рисунку 16 зображено графік зміни температури повітря протягом доби. Користуючись цим графіком, визначте:
1) якою була температура повітря о 2 год; о 8 год; о 12 год; о 16 год; о 22 год;
2) о котрій годині температура повітря була –3 °С; –4 °С; 0 °С;
3) якою була найнижча температура та о котрій годині;
4) якою була найвища температура та о котрій годині;
5) протягом якого проміжку часу температура повітря була нижчою від 0 °С; вищою за 0 °С;
6) протягом якого проміжку часу температура повітря підвищувалася; знижувалася.
Складіть за графіком таблицю зміни температури повітря протягом доби через кожні 2 год.
854.• Мотоцикліст виїхав із дому й через деякий час повернувся. На рисунку 17 зображено графік зміни відстані від мотоцикліста до дому залежно від часу (графік руху мотоцикліста). Користуючись графіком, визначте:
1) яку відстань проїхав мотоцикліст за першу годину руху;
2) на якій відстані від місця початку руху мотоцикліст зупинився відпочити першого разу; другого разу;
3) скільки часу тривала перша зупинка; друга зупинка;
4) на якій відстані від дому був мотоцикліст через 5 год після початку руху;
5) з якою швидкістю рухався мотоцикліст останні півгодини.
855.• Туристка вийшла з базового табору й через деякий час повернулася. На рисунку 18 зображено графік руху туристки.
1) На якій відстані від табору була туристка через 10 год після початку руху?
2) Скільки часу вона витратила на зупинку?
3) Через скільки годин після виходу туристка була на відстані 8 км від табору?
4) З якою швидкістю йшла туристка до зупинки?
5) З якою швидкістю йшла туристка останні 2 год?
856.• Кожному числу поставили у відповідність відстань від точки, що зображає це число на координатній прямій, до початку відліку. Поясніть, чому описане правило є функцією. Знайдіть її область визначення та область значень. Позначивши цю функцію буквою f, знайдіть f (2), f (–5), f (0).
857.• Розглянемо функцію g, задану таким правилом: кожному одноцифровому натуральному числу поставили у відповідність останню цифру його квадрата.
1) Запишіть, чому дорівнює g (7), g (3), g (1), g (9), g (4).
2) Знайдіть область визначення та область значень функції.
858.• Розглянемо правило, за яким числу 0 ставляться у відповідність усі парні числа, а числу 1 — усі непарні числа. Чи є це правило функцією?
859.• Придумайте функцію f, областю визначення якої є всі натуральні числа, а областю значень — три числа: 0, 1, 2. Знайдіть f (7), f (15), f (101).
860.• Розглянемо правило, за яким кожному натуральному числу поставили у відповідність остачу при діленні його на 7. Чи є це правило функцією? У разі ствердної відповіді знайдіть область визначення та область значень цієї функції.
861.• У таблиці наведено виміри температури повітря протягом доби через кожну годину[7]. Побудуйте за цими даними графік зміни температури.
|
Час доби, год |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
|
Температура, °C |
2 |
3 |
1 |
0 |
–2 |
–3 |
–5 |
–4 |
–2 |
0 |
1 |
4 |
7 |
|
|
Час доби, год |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
|
|
|
Температура, °C |
8 |
9 |
7 |
5 |
4 |
3 |
2 |
1 |
0 |
–2 |
–3 |
–6 |
Користуючись графіком, знайдіть, протягом якого часу температура повітря підвищувалася та протягом якого часу знижува- лася.
862.• Велосипедистка виїхала з дому на прогулянку. Перші 2 год вона їхала зі швидкістю 12 км/год, потім відпочивала годину й повернулася додому зі швидкістю 8 км/год. Побудуйте графік руху велосипедистки.
863.• У таблиці наведено дані про рівень води в річці порівняно з ординаром (середнім рівнем води) з 1 по 15 травня.
|
Дата |
Рівень води, см |
Дата |
Рівень води, см |
Дата |
Рівень води, см |
|
1 |
8 |
6 |
20 |
11 |
4 |
|
2 |
10 |
7 |
18 |
12 |
0 |
|
3 |
12 |
8 |
14 |
13 |
–3 |
|
4 |
15 |
9 |
10 |
14 |
–5 |
|
5 |
16 |
10 |
8 |
15 |
–6 |
Побудуйте графік зміни рівня води в річці за вказаний період.
864.• Початкова температура води була 6 °С. Під час нагрівання температура води підвищувалася щохвилини на 2 °С.
1) Запишіть формулу залежності температури T води від часу t її нагрівання.
2) Складіть таблицю значень температури T за час нагрівання від 0 хв до 10 хв із кроком 1 хв.
3) Побудуйте графік залежності температури води від часу нагрівання протягом перших 10 хв.
865.• Прямолінійна дорога проходить повз туристичний табір. Турист, перебуваючи на відстані 5 км від табору, почав рухатися цією дорогою зі швидкістю 4 км/год, віддаляючись від табору.
1) Знайдіть відстань s від табору, на якій перебуватиме турист через t год після початку руху. 2) Заповніть таблицю значень s:
|
t, год |
0 |
0,25 |
0,5 |
0,75 |
1 |
1,25 |
1,5 |
1,75 |
2 |
|
s, км |
|
|
|
|
|
|
|
|
|
3) Користуючись заповненою таблицею, побудуйте графік залежності відстані до табору від часу руху.
866.• В економічних дослідженнях часто використовують криву попиту. Крива попиту — це графік, який показує, як залежить попит на товар від його ціни. У таблиці наведено залежність попиту на картоплю в деякому регіоні (у тис. т) від ціни 1 кг картоплі.
|
Ціна 1 кг картоплі, грн |
8 |
9 |
10 |
11 |
12 |
13 |
|
Попит, тис. т |
15 |
12 |
10 |
6 |
4 |
1 |
Подайте дані, наведені в таблиці, графічно. Сполучивши отримані точки відрізками, побудуйте криву попиту на картоплю. 867.• У міській раді Сонячного міста представлено дві партії: партія Знайка й партія Незнайка. Усього в міській раді 20 місць. У таблиці наведено кількість депутатських місць, які отримала партія Знайка протягом 8 останніх виборів.
|
Вибори |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
Кількість депутатів від партії Знайка |
14 |
12 |
10 |
16 |
18 |
15 |
14 |
10 |
1) Складіть аналогічну таблицю для партії Незнайка.
2) Подайте дані кожної таблиці графічно в одній системі координат. Побудуйте «криві популярності» кожної партії, сполучивши отримані точки відрізками.
868.• У баку було 8 л гасу. Щохвилини в бак уливають 4 л.
1) Запишіть залежність кількості y літрів гасу в баку від часу x, протягом якого гас уливали в бак.
2) Накресліть графік зміни y, надаючи x значень від 0 до 10.
3) Користуючись графіком, визначте:
а) скільки літрів гасу буде в баку через 3 хв; через 5 хв;
б) через скільки хвилин у баку буде 40 л гасу.
4) Через скільки хвилин бак буде наповнено, якщо його місткість — 80 л?
869.• На складі було 100 т вугілля. Щодня на склад привозили 20 т вугілля.
1) Виразіть формулою залежність кількості m вугілля на складі від часу t.
2) Накресліть графік цієї залежності.
870.•• Який із наведених графіків (рис. 19) ілюструє залежність змінної y від змінної x, подану нижче:
1) вартість проїзду в автобусі зростає на 1 грн через кожні 10 км шляху (x км — довжина шляху, y грн — вартість проїзду);
2) металеву пружину розтягнули й відпустили (x с — час, y см — довжина пружини);
3) вартість полуниці на ринку протягом травня — червня (x днів — час, y грн — вартість)?
Рис. 19
 ВПРАВИ ДЛЯ ПОВТОРЕННЯ
ВПРАВИ ДЛЯ ПОВТОРЕННЯ
871. Розв’яжіть рівняння:
1) –1,2x + 7,2 = 0; 3) 3x + 1,5 = –2,5;
2) ![]() x 6 0; 4) 6 – 0,5x = 16.
x 6 0; 4) 6 – 0,5x = 16.
872. Розкладіть на множники вираз:
9 b6 −3mn 5 −16m 2n 4;
1) −
64
2) 20z 2 3xy 15xz 4yz;
3) 0,027a[8]2 +b9.
873. Доведіть, що при будь-якому натуральному значенні n значення виразу:
1) (n + 25) (n + 3) – (n + 6) (n + 4) – 6 ділиться націло на 9;
2) (13n – 24) (13n + 24) – (12n – 26) (12n + 26) ділиться націло на 25;
3) (9n + 2)2 – (3n – 2)2 ділиться націло на 24.
874. Відомо, що при деякому значенні x значення виразу 2x2 – 3x + + 1 дорівнює 2. Знайдіть значення виразу 10x2 – 15x – 20 при цьому значенні змінної x.
875. Знайдіть таке найменше натуральне значення a, при якому вираз x 2 4x 2a набуває додатних значень при будь-якому значенні x.
876. (Задача з «Теоретичного і практичного курсу чистої математики» Ю. Д. Войтяховського1.) Капітан на запитання, скільки має у своїй команді людей, відповів, що ![]() його команди в караулі,
його команди в караулі, ![]() — на роботі,
— на роботі, ![]() — у лазареті та 27 осіб у наявності. Запитання: скільки людей було в його команді?
— у лазареті та 27 осіб у наявності. Запитання: скільки людей було в його команді?
 УЧИМОСЯ РОБИТИ НЕСТАНДАРТНІ КРОКИ
УЧИМОСЯ РОБИТИ НЕСТАНДАРТНІ КРОКИ
877. Натуральні числа x і y такі, що 34x = 43y. Доведіть, що число x + y складене.

Приклади, розглянуті в попередньому пункті, показують, що функцію можна задавати різними способами.
Функцію вважають заданою, якщо вказано її область визначення та правило, за допомогою якого можна за кожним значенням незалежної змінної знайти значення залежної змінної.
Вам не раз доводилося формулювати різні правила. Оскільки функція — це правило, то його можна виразити словами. Такий спосіб задання функції називають заданням функції описом.
Наведемо кілька прикладів.
![]() ПРИКЛАД 1 Нехай незалежна змінна набуває будь-яких значень.
ПРИКЛАД 1 Нехай незалежна змінна набуває будь-яких значень.
Значення залежної змінної знаходимо за таким правилом: кожне значення незалежної змінної множимо на 2 і від отриманого добутку віднімаємо 1. Очевидно, що такий спосіб дає змогу однозначно знайти значення залежної змінної. Отже, ми задали деяку функцію f, областю визначення якої є всі числа. Наприклад, f (2) = 2æ2 – 1 = 3, f ![]() æ2 1 0, f (–13,4) = (–13,4)æ2 – 1 = –27,8
æ2 1 0, f (–13,4) = (–13,4)æ2 – 1 = –27,8
![]()
![]() ПРИКЛАД 2 Нехай незалежна змінна набуває будь-яких значень, крім 0. Відповідні значення залежної і незалежної змінних — взаємно обернені числа. Тут задано функцію f, область визначення якої — усі числа, крім 0. Наприклад, f (1) =1, f (3) =
ПРИКЛАД 2 Нехай незалежна змінна набуває будь-яких значень, крім 0. Відповідні значення залежної і незалежної змінних — взаємно обернені числа. Тут задано функцію f, область визначення якої — усі числа, крім 0. Наприклад, f (1) =1, f (3) = ![]() , f
, f ![]() 2 і т. п.
2 і т. п. ¤
Розглянемо найпоширеніший спосіб задання функції: задання функції за допомогою формули.
Якщо в прикладі 1 незалежну змінну позначити буквою x, а залежну — буквою y, указати область визначення — усі числа, то формула y 2x 1 задає вищеописану функцію.
Зрозуміло, що функцію з прикладу 2 задає формула y = 1 , де
x
x — будь-яке число, крім 0.
Якщо функцію задано формулою, права частина якої — цілий вираз, і при цьому не вказано область визначення, то вважатимемо, що областю визначення такої функції є всі числа. Наприклад, формули y = x 2, y x 3, y x2 x 2 задають функції, областю ви-
5
значення кожної з яких є всі числа.
Якщо, наприклад, функцію задано формулою y = x 3, то просто говорять, що задано функцію y = x 3.
Якщо хочуть наголосити, що, наприклад, формула y 5 x за-
3
дає деяку функцію f, то пишуть: f (x) 5 x .
3
Якщо хочуть наголосити, що, наприклад, формула s = 10t + 2 задає функцію з аргументом t і залежною змінною s, то пишуть: s (t) = 10t + 2.
Розглянемо функцію f (x) x 2x 2, область визначення якої складається із чисел −1, 0, ![]() , 1, 3. Маємо:
, 1, 3. Маємо:
|
f ( 1) 3, f (0) = 0, f Отримані результати занесемо до таблиці: |
15. |
|
||||
|
x |
–1 |
0 |
|
|
1 |
3 |
|
f (x) |
–3 |
0 |
0 |
|
–1 |
–15 |
Усі числа, записані в першому рядку цієї таблиці, складають область визначення даної функції f. Таблиця дає змогу за вказаним значенням аргументу однозначно знайти відповідне значення функції. Отже, ця таблиця — ще один спосіб задання функції f. Його називають табличним.
Цей спосіб зручно використовувати в тих випадках, коли область визначення функції складається з кількох чисел.
![]() ПРИКЛАД 3 Функцію задано формулою y = 5x + 2. Знайдіть значення аргументу, при якому значення функції дорівнює 12.
ПРИКЛАД 3 Функцію задано формулою y = 5x + 2. Знайдіть значення аргументу, при якому значення функції дорівнює 12.
![]() Розв’язання. Підставивши у формулу y = 5x + 2 замість y число 12, отримуємо рівняння 5x + 2 = 12, звідки x = 2. Відповідь: 2.
Розв’язання. Підставивши у формулу y = 5x + 2 замість y число 12, отримуємо рівняння 5x + 2 = 12, звідки x = 2. Відповідь: 2. ¤
ПРИКЛАД 4 Функцію f задано таким чином: f (x) = x + 7, якщо x m−1, і f (x) = 2, якщо x > –1. Знайдіть значення функції f, яке
відповідає аргументу: 1) –2; 2) –1; 3) 1.
Розв’язання. 1) Оскільки −2 m−1, то значення функції в точці x = –2 обчис люється за формулою f (x) = x + 7. Отже, f (–2) = = –2 + 7 = 5.
2) Оскільки −1 m−1, то f (–1) = –1 + 7 = 6.
3) Оскільки 1 > –1, то f (1) = 2.
Для задання даної функції використовують форму запису за допомогою фігурної дужки:
x 7, якщоx m 1, f (x)
![]() 2, якщо x 1.
2, якщо x 1. ¤
![]() ПРИКЛАД 5 Функції задано формулами y = 4x + 1 і y = 2x – 7. При якому значенні аргументу ці функції набувають рівних значень?
ПРИКЛАД 5 Функції задано формулами y = 4x + 1 і y = 2x – 7. При якому значенні аргументу ці функції набувають рівних значень?
Розв’язання. Щоб знайти шукане значення аргументу, розв’яжемо рівняння 4x + 1 = 2x – 7. Маємо: 4x – 2x = –7 – 1;

878.° Прочитайте запис, укажіть аргумент функції та залежну змінну:
1) s (t) = 70t; 3) V (a) = a 3;
2) y (x) = –2x + 4; 4) f (x) x 2 4.
879.° Функцію задано формулою y = 10x + 1. Знайдіть значення y, якщо:
1) x = –1; 2) x = 3; 3) x ![]() ; 4) x = 7.
; 4) x = 7.
880.° Функцію задано формулою f (x) = 3 – 4x. Чи є правильною рівність:
1) f (–2) = –5; 2) f ![]() 1; 3) f (0) = –1; 4) f (–1) = 7?
1; 3) f (0) = –1; 4) f (–1) = 7?
881.° Функцію задано формулою f (x) = 7x – 5. Знайдіть:
1) f (2); 2) f (0); 3) f (–3); 4) f (200).
882.° Функцію задано формулою f (x) = 2x2 – 1. Чи є правильною рівність:
|
1) f (1) = 1; |
4) f (0) = 0; |
|
2) f (4) = 15; |
5) f (–1) = 1; |
|
3) f (–2) = –9; |
6) f (–5) = 19? |
883.° Функцію задано формулою y x 2 3. Знайдіть значення y, якщо:
1) x = 5; 3) x = 0,1; 2) x = –4; 4) x = 0.
884.° Функцію задано формулою f (x) = 3 + 4x. Знайдіть значення x, при якому:
1) f (x) = 19; 3) f (x) = 0; 2) f (x) = –3; 4) f (x) = 323.
885.° Функцію задано формулою f (x) = –0,1x – 2. Знайдіть значення x, при якому:
1) f (x) = 1; 3) f (x) = –43,6.
2) f (x) = –100;
886.° Функцію задано формулою y ![]() x 2. Знайдіть:
x 2. Знайдіть:
1) значення функції для значень аргументу 12, 6, –6, 0, 1, 2, –4, –3;
2) значення аргументу, при якому значення функції дорівнює 4, 3, 0, –1.
887.° Функцію задано формулою f (x) = 2x – 1.
1) Знайдіть f (3), f (–4), f (0), f (–0,5), f (3,2).
2) Знайдіть значення x, при якому f (x) = 7, f (x) = –9, f (x) = 0, f (x) 2,4.
3) Чи є правильною рівність: f (5) = 9, f (0,3) = 0,4, f (–3) = –7? 888.° Функцію задано формулою y = x (x + 8). Заповніть таблицю:
![]()
889.° Функцію задано формулою y ![]() x . Заповніть таблицю:
x . Заповніть таблицю:
![]()
890.° Функцію задано формулою y = x2 + x + 1. Заповніть таблицю:
|
x |
–3 |
–2 |
–1 |
0 |
1 |
2 |
4 |
7 |
|
y |
|
|
|
|
|
|
|
|
891.° Кожному натуральному числу, яке більше за 10, але менше від 20, поставили у відповідність остачу при діленні цього числа на 6.
1) Яким способом задано цю функцію?
2) Яка область значень цієї функції?
3) Задайте цю функцію табличним способом.
892.° Область визначення деякої функції — усі двоцифрові натуральні числа, які кратні 10, а значення функції у 5 разів менші від відповідних значень аргументу. Задайте цю функцію формулою та табличним способом.
893.° Область визначення деякої функції — одноцифрові натуральні числа, а значення функції у 2 рази більші за відповідні значення аргументу.
1) Яким способом задано цю функцію?
2) Задайте цю функцію формулою та табличним способом.
894.• Задайте формулою функцію, якщо значення функції: 1) протилежні відповідним значенням аргументу;
2) дорівнюють потроєним відповідним значенням аргументу; 3) на 4 більші за квадрати відповідних значень аргументу.
895.• Задайте формулою функцію, якщо значення функції:
1) на 3 менші від відповідних значень аргументу;
2) на 5 більші за подвоєні відповідні значення аргументу.
896.• Складіть із кроком 0,5 таблицю значень функції, заданої формулою y = x2 + 2x, де –1 m х m 3.
897.• Складіть із кроком 1 таблицю значень функції, заданої формулою y = x3 – 1, де –3 m х m 2.
898.• Функцію задано формулою y = 0,2x – 5. Заповніть таблицю відповідних значень x і y:
|
x |
4 |
|
–1,5 |
|
–3 |
|
y |
|
2 |
|
–1,4 |
|
899.• Дано функцію y 8 ![]() x. Заповніть таблицю:
x. Заповніть таблицю:
|
x |
14 |
|
–1,4 |
|
|
y |
|
0 |
|
9 |
900.• Дано функції g (x) 20 3 і h (x) = 8 – 3x. Порівняйте:
x
1) g (1) і h (1); 2) g (5) і h (2); 3) g (–2) і h (6).
2x 1, якщо x m 2,
901.• Дано функцію f (x) x 2, якщо 2 x 3, 6, якщо x l3.
Знайдіть: 1) f (–3); 2) f (–2); 3) f (2); 4) f (3); 5) f (2,9); 6) f (8,1).
• 2x 4, якщо x 0,
902. Знайдіть значення функції y яке від0,1x 5, якщо x m0,
повідає аргументу:
1) 3; 2) 0,001; 3) 0; 4) –8.
903.• Функцію задано за допомогою таблиці:
|
x |
2 |
4 |
6 |
8 |
|
y |
5 |
7 |
9 |
11 |
1) Які числа складають область визначення цієї функції? 2) Задайте цю функцію описом і формулою. 904.• Функцію задано за допомогою таблиці:
|
x |
1 |
3 |
5 |
7 |
9 |
|
y |
0,5 |
1,5 |
2,5 |
3,5 |
4,5 |
1) Які числа складають область визначення цієї функції?
2) Задайте цю функцію описом і формулою.
905.• Функції задано формулами y x 2 8x і y = 4 – 8x. При яких значеннях аргументу ці функції набувають рівних значень?
906.• Функцію задано формулою f (x) = 3x + 5. При якому значенні x значення функції дорівнює значенню аргументу?
907.• Функцію задано формулою y x 2 2x 1. При яких значеннях x значення функції дорівнює подвоєному значенню аргументу?
908.* Функцію f задано описом: значення функції дорівнює найбільшому цілому числу, яке не більше за відповідне значення аргументу[9]. Знайдіть f (3,7), f (0,64), f (2), f (0), f (–0,35), f (–2,8).
![]()
909. Цього року фермер скоротив площу під капусту на 10 %. Урожайність капусти цього року підвищилася на 12 % порівняно з минулим роком. Збільшився чи зменшився врожай капусти порівняно з минулим роком і на скільки відсотків?
910. Яке з даних рівнянь: а) має один корінь; б) має два корені;
в) має безліч коренів; г) не має жодного кореня: 1) 3,4 (1 + 3x) – 1,2 = 2 (1,1 + 5,1x);
2) | 2x – 1 | = 17,3;
3) 3 (| x – 1 | – 6) + 21 = 0;
4) 0,2 (7 – 2x) = 2,3 – 0,3 (x – 6)?
911. Дано три числа, з яких кожне наступне на 10 більше за попереднє. Знайдіть ці числа, якщо добуток найбільшого та середнього з них на 320 більший за добуток найбільшого та найменшого із цих чисел.
912. Доведіть, що коли a + c = 2b, то a 2 8bc (2b c)2.
913. Відомо, що x y a2 , y + z = –a, x + z = 1. Доведіть, що вираз 4
x + y + z набуває тільки невід’ємних значень.
![]() ГОТУЄМОСЯ ДО ВИВЧЕННЯ НОВОЇ ТЕМИ
ГОТУЄМОСЯ ДО ВИВЧЕННЯ НОВОЇ ТЕМИ
914. Побудуйте пряму, яка проходить через точки A (–2; 3) і B (4; 3). Чому дорівнюють ординати точок цієї прямої?
915. Побудуйте пряму, яка проходить через точки C (3; 0) і D (3; –4). Чому дорівнюють абсциси точок цієї прямої?
Поновіть у пам’яті зміст п. 34 на с. 274, 275.
 УЧИМОСЯ РОБИТИ НЕСТАНДАРТНІ КРОКИ
УЧИМОСЯ РОБИТИ НЕСТАНДАРТНІ КРОКИ
916. Доведіть, що в будь-якому 60-цифровому числі, десятковий запис якого не містить нулів, можна закреслити кілька цифр таких, що отримане в результаті цього число буде ділитися націло на 1001.
Розглянемо функцію y = x2 – 4x, де −1 mx m4. Складемо таблицю значень цієї функції при цілих значеннях аргументу:
|
x |
–1 |
0 |
1 |
2 |
3 |
4 |
|
y |
5 |
0 |
–3 |
–4 |
–3 |
0 |
Розглянемо пари чисел, записаних у кожному стовпці цієї таблиці, як координати (x; y) точок координатної площини. При цьому значення аргументу є абсцисою точки, а відповідне значення функції — її ординатою.
Ці точки зображено на рисунку 20.
Очевидно, що, надаючи аргументу інших значень (відмінних від цілих) з області визначення та знаходячи відповідні значення функції, можна позначити все більше й більше точок на координатній площині (рис. 21, 22).
Усі точки координатної площини, які можна позначити, діючи в такий спосіб, утворюють графік функції.
Означення. Графіком функції f називають геометричну фігу ру, що складається з усіх тих і тільки тих точок координатної площини, абсциси яких дорівнюють значенням аргументу, а ординати — відповідним значенням функції f.
Очевидно, що реалізувати на практиці описаний метод побудови графіка функції y = x2 – 4x неможливо. Адже точок, які треба
![]() було б позначити, безліч. Проте, якщо позначити досить багато точок, а потім сполучити їх плавною лінією, то отримана крива (рис. 23) буде тим менше відрізнятися від шуканого графіка, чим більше точок ми позначимо.
було б позначити, безліч. Проте, якщо позначити досить багато точок, а потім сполучити їх плавною лінією, то отримана крива (рис. 23) буде тим менше відрізнятися від шуканого графіка, чим більше точок ми позначимо.
Оскільки описаний метод побудови графіка функції передбачає значну технічну роботу, то істотну її частину може взяти на себе комп’ютер. Сьогодні існує багато програм, призначених для побудови графіків. Так, на екрані монітора (рис. 24) зображено
графік функції y = x 3, де −2 mx m2. Рис. 23

Рис. 24
Наголосимо, що коли якась фігура є графіком функції f, то виконуються дві умови:
1) якщо x0 — деяке значення аргументу, а f (x0) — відповідне значення функції, то точка з координатами (x0; f (x0)) обов’язково належить графіку;
2) якщо (x0; y0) — координати довільної точки графіка, то x0 і y0 — відповідні значення незалежної і залежної змінних функції f, тобто y0 = f (x0).
Графіком функції не обов’язково є лінія. На рисунку 25 зображено графік функції, заданої таблицею:
|
x |
1 |
–2 |
|
y |
3 |
0 |
Він складається з двох точок.
Розглянемо приклад побудови графіка функції, заданої описом.
Нехай область визначення даної функції — усі числа. Для кожного додатного аргументу значення функції дорівнює 1; для кожного від’ємного аргументу значення функції дорівнює –1; якщо аргумент дорівнює нулю, то значення функції дорівнює нулю. Графік цієї функції зображено на рисунку 26. Він складається з трьох частин: точки O (0; 0) і двох променів, у кожного з яких «виколото» початок.
Не будь-яка фігура, зображена на координатній площині, може слугувати графіком функції. Наприклад, коло не може бути графіком функції, оскільки за заданим значенням змінної x не завжди однозначно знаходиться значення змінної y (рис. 27).
Фігура, зображена на координатній площині, може бути графіком функції, якщо будь-яка пряма, перпендикулярна до осі абсцис, має із цією фігурою не більше ніж одну спільну точку. Можна говорити, що ця фігура задає деяку функцію. Такий спосіб задання функції називають графічним. Абсциси й ординати всіх точок цієї фігури утворюють відповідно область визначення та область значень функції.
Якщо функцію задано графічно, то значення функції за заданим значенням x0 аргументу можна знайти за таким правилом: через точку (x0; 0) провести пряму, перпендикулярну до осі абсцис, а потім знайти ординату точки перетину цієї прямої з графіком. Знайдена ордината дорівнює f (x0) (рис. 28).
Рис. 28 Рис. 29
Рисунок, схема, фотографія якогось об’єкта або процесу дають про нього наочне уявлення. Ту саму роль відіграє для функції її графік. Так, вивчаючи графік, зображений на рисунку 29, можна, наприклад, знайти:
1) область визначення функції: усі x такі, що −3 mx m6;
2) область значень функції: усі y такі, що −2 my m4;
3) значення аргументу, при яких значення функції дорівнює нулю: x 3 або x =1;
4) значення аргументу, при яких функція набуває додатних значень: 1 < x m6;
5) значення аргументу, при яких функція набуває від’ємних значень: –3 < x < 1.
Після вивчення матеріалу цього пункту стає зрозуміло, чому в техніці, медицині, економіці та багатьох інших сферах людської діяльності так широко використовують комп’ютерні програми, які дозволяють будувати графіки різноманітних функціональних залежностей.
![]() ПРИКЛАД 1 Чи належить графіку функції, заданої формулою y = x – 6, точка: 1) A (8; 2); 2) B (2; 4)?
ПРИКЛАД 1 Чи належить графіку функції, заданої формулою y = x – 6, точка: 1) A (8; 2); 2) B (2; 4)?
Розв’язання. Щоб установити, чи належить точка графіку функції, знайдемо значення функції, коли значення аргументу дорівнює абсцисі даної точки. Якщо значення функції дорівнюватиме ординаті даної точки, то точка належить графіку, а якщо ні, то не належить.
1) При x = 8 маємо: y = 8 – 6 = 2. Отже, точка A належить графіку даної функції.
2) ![]() При x = 2 маємо: y = 2 – 6 = –4 ≠ 4. Отже, точка B не належить графіку функції y = x – 6.
При x = 2 маємо: y = 2 – 6 = –4 ≠ 4. Отже, точка B не належить графіку функції y = x – 6. ¤
![]() ПРИКЛАД 2 Не виконуючи побудови, знайдіть координати точок перетину графіка функції y = x2 – 4 з осями координат.
ПРИКЛАД 2 Не виконуючи побудови, знайдіть координати точок перетину графіка функції y = x2 – 4 з осями координат.
Розв’язання. Точка належить осі абсцис тоді й тільки тоді, коли її ордината дорівнює нулю. Тому, щоб знайти координати точки пере тину графіка даної функції з віссю абсцис, треба розв’язати рівняння x2 – 4 = 0. Маємо: x = 2 або x = –2. Отже, графік даної функції має з віссю абсцис дві спільні точки: A (2; 0) і B (–2; 0).
Точка належить осі ординат тоді й тільки тоді, коли її абсциса дорівнює нулю. Тому, щоб знайти координати точки перетину графіка функції з віссю ординат, треба знайти значення даної функції при x = 0. Маємо: y = –4. Отже, графік функції перетинає вісь ординат у точці C (0; –4). ¤
1. Що називають графіком функції?
2. ![]() Які дві умови мають виконуватися, щоб фігура була графіком функції f ?
Які дві умови мають виконуватися, щоб фігура була графіком функції f ?
3. Чи може графік функції складатися з однієї точки?
4. Чи будьяка фігура на координатній площині може слугувати графіком функції?
5. наведіть приклад фігури, яка не може бути графіком функції.
6. Скільки спільних точок може мати з графіком функції будьяка пряма, перпендикулярна до осі абсцис?
ВПРАВИ
917.° Користуючись графіком функції y = f (x), зображеним на рисунку 30, заповніть таблицю:
|
x |
–3 |
–2 |
0 |
2 |
6 |
7 |
|
y |
|
|
|
|
|
|
Рис. 30
918.° Користуючись графіком функції y = f (x), зображеним на рисунку 31, заповніть таблицю:
|
x |
–2 |
–1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
f (x) |
|
|
|
|
|
|
|
|
|
919.° Користуючись графіком функції y = f (x), зображеним на рисунку 30, знайдіть:
1) значення аргументу, при яких y = 3;
2) значення аргументу, при яких значення функції дорівнює нулю;
3) область визначення функції;
4) область значень функції;
5) значення аргументу, при яких функція набуває від’ємних значень;
6) значення аргументу, при яких функція набуває додатних значень.
920.° На рисунку 32 зображено графік функції y = f (x). Користуючись графіком, знайдіть:
1) значення y, якщо x = –3,5; –1,5; 2; 4;
2) значення x, яким відповідають значення y = –3; –1,5; 2;
3) значення аргументу, при яких значення функції дорівнюють нулю;
4) область визначення та область значень функції;5) значення аргументу, при яких значення функції додатні; 6) значення аргументу, при яких значення функції від’ємні.
921.° Користуючись графіком функції y = f (x), зображеним на рисунку 33, знайдіть: 1) область визначення функції;
2) область значень функції;
3) координати точок перетину графіка функції з віссю абсцис;
4) координати точки перетину графіка функції з віссю ординат;
5) значення аргументу, при яких функція набуває від’ємних значень;
6) значення аргументу, при яких функція набуває додатних значень.
Рис. 33
922.° На рисунку 34 зображено графік функції y = f (x). Користуючись графіком, знайдіть:
1) f (–4); f (–2,5); f (0,5); f (2);
2) значення x, при яких f (x) = 2,5; f (x) = 1; f (x) = 0;
3) область визначення та область значень функції; 4) значення аргументу, при яких значення функції додатні; 5) значення аргументу, при яких значення функції від’ємні.
923.° Чи належить графіку функції y x2 2 точка:
1) A (0; 2); 2) B (–1; 1); 3) C (–2; 6); 4) D (–3; –7)?
924.° Чи належить графіку функції y 2x2 1 точка:
1) A ![]() ; 1,5 ; 2) B (–3; 17)?
; 1,5 ; 2) B (–3; 17)?
925.° Назвіть координати кількох точок, які належать графіку функції:
1) y = 7x – 4; 2) y x 2 1; 3) y = 4 – | x |.
926.° Графікам яких із даних функцій належить точка A (1; 2):
1) y = 1 – 2x; 2) y = x2 + 1; 3) y = 2 ; 4) y = 0,3x + 0,7?
x
927.° Чи належить графіку функції y x точка:
3
1) A (9; –3); 2) B (6; 2); 3) C (–1; 3); 4) D (–12; 4)?
928.° Які з фігур, зображених на рисунку 35, можуть бути графіками функцій з аргументом х?
Рис. 35
929.° Яка з фігур, зображених на рисунку 36, може бути графіком функції з аргументом х?

а б
Рис. 36
930.• Графіком деякої функції є ламана ABCD з вершинами в точках A (–3; 6), B (–1; 2), C (3; –2), D (9; 0).
1) Побудуйте графік даної функції.
2) Знайдіть значення функції, якщо значення аргументу дорівнює: –2; 0; 2; 6.
3) Знайдіть значення аргументу, при якому значення функції дорівнює: 1; –1; 0.
931.• Чи може ламана ABC бути графіком деякої функції, якщо:
1) A (–4; –1), B (1; 2), C (2; 4); 2) A (–4; –1), B (1; 2), C (1; 3)?
932.• Графіком деякої функції є ламана MKE, де M (–4; 1), K (2; 4), E (5; –2).
1) Побудуйте графік даної функції.
2) Знайдіть значення функції, якщо значення аргументу дорівнює: –2; 0; 3.
3) Знайдіть значення x, при якому y = –2; 0; 2.
933.• Функцію задано формулою y x 2 1, де −2 mx m3.
1) Складіть таблицю значень функції з кроком 1.
2) Побудуйте графік функції, користуючись складеною таблицею.
3) Користуючись графіком, знайдіть значення аргументу, при яких значення функції менші від нуля, а при яких — більші за нуль.
4) Користуючись графіком функції, укажіть область значень функції.
934.• Функцію задано формулою y 4 x 2, де −3 mx m2.
1) Складіть таблицю значень функції з кроком 1.
2) Побудуйте графік функції, користуючись складеною таблицею.
3) Користуючись графіком, знайдіть значення аргументу, при яких значення функції менші від нуля, а при яких — більші за нуль.
4) Користуючись графіком функції, укажіть область значень функції.
935.• Значення функції y = f (x) дорівнюють 0 при значеннях аргументу, що дорівнюють –5 і 4. Яке з наведених тверджень є правильним:
1) графік функції має з віссю ординат дві спільні точки (0; –5) і (0; 4);
2) графік функції має з віссю абсцис дві спільні точки (–5; 0) і (4; 0)?
936.• Не виконуючи побудови, знайдіть координати точок перетину з осями координат графіка функції:
1) y x 2 16x ; 3) y x 3 9x ;
2) y = | x | – 2; 4) y = 0,8x.
937.• Не виконуючи побудови, знайдіть координати точок перетину з осями координат графіка функції:
1) y = 36 – 9x; 2) y x 2 x ; 3) y 49 x 2.
938.• Задано функцію y = 1 – x, областю визначення якої є всі одноцифрові натуральні числа. Побудуйте графік цієї функції.
939.• Побудуйте графік функції f (x) = 1,5x + 1, областю визначення якої є цілі числа, при яких виконується нерівність −4 mx m2.
940.* Побудуйте графік функції, областю визначення якої є всі натуральні числа та яка набуває значення 1 при парних значеннях аргументу та значення –1 при непарних значеннях аргументу.
941.* Функцію f задано описом: значення функції дорівнює найбільшому цілому числу, яке не більше за відповідне значення аргументу. Побудуйте графік цієї функції.
![]()
942. Трактористи Іван і Петро, працюючи разом, можуть зорати поле за 21 год, трактористи Петро й Остап — за 28 год, а Іван і Остап — за 20 год. За який час Іван, Петро й Остап можуть зорати це поле, працюючи втрьох?
943. Спростіть вираз:
1) (c + 2) (c – 3) – (c + 1) (c + 3); 3) 3 (x −5)2 −(8x 2 −10x);
2) (p 4) (p 11) (p 6)2; 4) 7 (2y −5)2 −2 (7y −1)2.
944. Доведіть тотожність:
1) (4a 2 3)2 (7 4a 2)2 2 (4a 2 3) (4a 2 7) 100; 2) (a 2 6ab 9b2) (a 2 6ab 9b2) (a 2 9b2)2 0.
945. Доведіть, що при будь-якому непарному значенні n значення виразу (4n 1)2 (n 4)2 кратне 120.
946. Знайдіть які-небудь три натуральних значення змінної x таких, щоб вираз a2 −2x можна було розкласти на множники за формулою різниці квадратів. Отримані вирази розкладіть на множники.
947. (Задача Бхаскари[10].) Є кадамба-квітка; на одну пелюстку бджілок п’ята частина сіла. Поряд росла вся у цвіту симендга, і на ній третя частина розмістилася. Різницю їхню ти знайди, тричі її ти додай, на кумай цих бджіл посади. Лише бджілка
одна не знайшла собі місця ніде, усе літала туди-сюди та скрізь пахощами квітів тішилася. Тепер скажи мені: скільки бджілок усього тут зібралося?
![]() ГОТУЄМОСЯ ДО ВИВЧЕННЯ НОВОЇ ТЕМИ
ГОТУЄМОСЯ ДО ВИВЧЕННЯ НОВОЇ ТЕМИ
948. У таблиці наведено відповідні значення величин x і y. Установіть, чи є ці величини прямо пропорційними.
|
x |
2 |
5 |
7 |
9 |
2) |
x |
0,4 |
1,8 |
2,3 |
3,1 |
|
y |
6 |
15 |
21 |
27 |
y |
0,8 |
3,8 |
4,6 |
6,2 |
1)
949. Заповніть таблицю, якщо величина y прямо пропорційна величині x.
|
x |
0,3 |
8 |
3,2 |
|
|
|
y |
|
|
9,6 |
2,7 |
42 |
Поновіть у пам’яті зміст п. 33 на с. 274.
 УЧИМОСЯ РОБИТИ НЕСТАНДАРТНІ КРОКИ
УЧИМОСЯ РОБИТИ НЕСТАНДАРТНІ КРОКИ
950. Із квадратного аркуша паперу в клітинку, який містить цілу кількість клітинок, вирізали по лініях квадрат, що містить цілу кількість клітинок, так, що залишилася 71 клітинка. Скільки клітинок було на початковому аркуші паперу?
![]() 23. Лінійна функція, її графік і властивості
23. Лінійна функція, її графік і властивості
Розглянемо два приклади.
![]() ПРИКЛАД 1 У басейні було 200 л води. Протягом t хв до басейну наливається щохвилини 80 л води. Тоді об’єм V води в басейні до
ПРИКЛАД 1 У басейні було 200 л води. Протягом t хв до басейну наливається щохвилини 80 л води. Тоді об’єм V води в басейні до
його заповнення можна обчислити за формулою V = 80t + 200, де t l0.
![]() Ця формула задає функціональну залежність змінної V від змінної t.
Ця формула задає функціональну залежність змінної V від змінної t. ¤
![]()
![]() ПРИКЛАД 2 Перша бригада зібрала 25 ящиків яблук; кожний робітник другої бригади зібрав по 2 ящики. Нехай у другій бригаді було x робітників. Позначимо кількість усіх ящиків, зібраних двома бригадами, буквою y. Тоді залежність змінної y від змінної x виражається формулою y 2x 25, де x — натуральне число.
ПРИКЛАД 2 Перша бригада зібрала 25 ящиків яблук; кожний робітник другої бригади зібрав по 2 ящики. Нехай у другій бригаді було x робітників. Позначимо кількість усіх ящиків, зібраних двома бригадами, буквою y. Тоді залежність змінної y від змінної x виражається формулою y 2x 25, де x — натуральне число. ¤
У наведених прикладах ми побудували функції, що описують дві різні реальні ситуації. Проте ці функції схожі в тому, що формули, які їх задають, мають вигляд y kx b.
Означення. Функцію, яку можна задати формулою виду y =kx + b, де k і b — деякі числа, x — незалежна змінна, називають лінійною.
Ось ще приклади лінійних функцій:
y 2x 1, y 1 x, y =5x, y =2.
Зауважимо, що областю визначення лінійної функції є всі числа.
Побудуємо графік функції y 2x 1.
Складемо таблицю значень цієї функції для деяких значень аргументу:
|
x |
–3 |
–2 |
–1 |
0 |
1 |
2 |
3 |
|
y |
7 |
5 |
3 |
1 |
–1 |
–3 |
–5 |
Точки A (−3;7), B (−2; 5), C (−1; 3), D (0;1), E (1; −1), F (2; −3), G (3; −5) належать шуканому графіку (рис. 37). Усі ці точки лежать на одній прямій, яка є графіком функції y 2x 1 (рис. 38).
Рис. 37 Рис. 38
У курсі геометрії 9 класу ви доведете, що графіком лінійної функції є пряма.
Зазначимо, що ця пряма не може бути вертикальною, тобто прямою, перпендикулярною до осі абсцис. Справді, вертикальна пряма не може слугувати графіком функції.
Оскільки пряму можна однозначно задати будь-якими двома її точками, то для побудови графіка лінійної функції достатньо вибрати два довільних значення аргументу й скласти таблицю значень функції, яка має лише два стовпці.
![]() ПРИКЛАД 3 Побудуйте графік функції y = –3x + 2.
ПРИКЛАД 3 Побудуйте графік функції y = –3x + 2.
Розв’язання. Складемо таблицю значень даної функції для двох довільних значень аргументу:
|
x |
0 |
1 |
|
y |
2 |
–1 |
![]() Позначимо на координатній площині точки (0; 2) і (1; –1) та проведемо через них пряму (рис. 39). Ця пряма є графіком лінійної функції y = –3x + 2.
Позначимо на координатній площині точки (0; 2) і (1; –1) та проведемо через них пряму (рис. 39). Ця пряма є графіком лінійної функції y = –3x + 2.
У формулі y kx b, яка задає лінійну функцію, припустимими є й випадки, коли k = 0 та/або b = 0.
Розглянемо випадок, коли b = 0 і k ≠ 0. Тоді формула набуває вигляду y = kx. Звідси для всіх значень аргументу, відмінних від нуля, можна записати, що Рис. 39 y
= k. Ця формула показує, що для функції y = kx при x ≠ 0 від-
x
ношення відповідних значень залежної та незалежної змінних залишається сталим і дорівнює k.
![]() Нагадаємо, що в курсі математики 6 класу ви вже ознайомилися з подіб ними залежностями між величинами. Таку залежність називають прямою пропорційністю. Тому лінійну функцію, яку задають формулою y = kx, де k ≠0, також називають прямою пропорційністю.
Нагадаємо, що в курсі математики 6 класу ви вже ознайомилися з подіб ними залежностями між величинами. Таку залежність називають прямою пропорційністю. Тому лінійну функцію, яку задають формулою y = kx, де k ≠0, також називають прямою пропорційністю.
Функції y = 2x , y = x, y x, y ![]() x — приклади прямих пропорційностей.
x — приклади прямих пропорційностей.
Оскільки пряма пропорційність є окремим випадком лінійної функції (це ілю-
Рис. 40 струє схема, зображена на рисунку 40), то
її графік — пряма. Особливість цієї прямої полягає в тому, що вона при будь-якому значенні k проходить через точку O (0; 0). Справді, якщо у формулі y = kx покласти x = 0, то отримаємо y = 0. Тому для побудови графіка прямої пропорційності достатньо знайти яку-небудь точку графіка, відмінну від початку координат, і провести пряму через цю точку й точку O (0; 0).
На рисунку 41 зображено графіки прямих пропорційностей, які наводилися вище як приклади.

Розглянемо ще один окремий випадок лінійної функції. У формулі y kx b покладемо k = 0. Отримаємо y = b. Зрозу-
![]() міло, що в цьому разі значення функції залишатимуться незмінними при будь-яких змінах значень аргументу.
міло, що в цьому разі значення функції залишатимуться незмінними при будь-яких змінах значень аргументу.
ПРИКЛАД 4 Побудуйте графік функції y = 2.
Розв’язання. Як і для побудови графіка будь-якої лінійної функції, треба зна-
Рис. 42 ти дві точки, які належать йому. Ці точки матимуть однакові ординати, які дорівню-
![]() ють 2. Їхні абсциси виберемо довільно, наприклад –2 і 0. Залишається провести пряму через точки A (–2; 2) і B (0; 2) (рис. 42). Ця пряма паралельна осі абсцис.
ють 2. Їхні абсциси виберемо довільно, наприклад –2 і 0. Залишається провести пряму через точки A (–2; 2) і B (0; 2) (рис. 42). Ця пряма паралельна осі абсцис. ¤
Зауважимо, що графіком функції y = 0 є вісь абсцис. Графіком функції y = b, де b ≠ 0, є пряма, паралельна осі абсцис.
|
Розв’язання. Графік даної функції перетинає вісь ординат у точці (0; 4). Підставивши координати цієї точки у формулу y = kx + b, отримуємо: 4 = kæ0 + b, звідки b = 4. Оскільки даний графік перетинає вісь абсцис у точці (3; 0), то, підставивши її координати Рис. 43 у формулу y = kx + 4, матимемо: 3k + 4 = 0; k = −
|

951.° Чи є лінійною функція, задана формулою:
|
1) y = 3x – 2; |
4) y |
3 x |
2; |
7) y = x ; 5 |
|
2) y = 8 – 7x; |
5) y |
2x 2 |
4; |
8) y = –4; |
![]() 3) y x 2; 6) y; 9) y = 0?
3) y x 2; 6) y; 9) y = 0?
3
У разі ствердної відповіді вкажіть значення коефіцієнтів k і b.
952.° Чи є прямою пропорційністю функція, задана формулою:
1) y = 4x; 4) y = 0;
2) y = 4 ; 5) y = –4x;
x
3) y = x ; 6) y x ?
4 4
У разі ствердної відповіді вкажіть значення коефіцієнта k.
953.° Лінійну функцію задано формулою y = 6x – 5. Заповніть таблицю:
|
x |
–3 |
–2 |
–1 |
0 |
1 |
2 |
3 |
|
y |
|
|
|
|
|
|
|
954.° Функцію задано формулою y = –2x + 5. Знайдіть:
1) значення функції, якщо значення аргументу дорівнює: –4; 3,5; 0;
2) значення аргументу, при якому значення функції дорівнює: 9; –5; 0.
955.° Функцію задано формулою y = 0,4x + 3. Заповніть таблицю:
|
x |
–2 |
|
0 |
|
5 |
|
|
y |
|
–2 |
|
0 |
|
–13 |
956.° Функцію задано формулою y = 0,3x – 2. Знайдіть:
1) значення функції, якщо значення аргументу дорівнює:
5; –2; 0;
2) значення аргументу, при якому значення функції дорівнює: 1; –11; 0,8.
957.° Заповніть таблицю та побудуйте графік функції:
1) y = x + 3; 2) y ![]() x 5.
x 5.
|
x |
0 |
1 |
|
x |
0 |
3 |
|
y |
|
|
y |
|
|
958.° Заповніть таблицю та побудуйте графік функції:
1) y = 3 – 0,5x; 2) y ![]() x 1.
x 1.
|
x |
0 |
2 |
|
x |
0 |
8 |
|
y |
|
|
y |
|
|
959.° Побудуйте графік функції:
1) y = x – 5; 3) y ![]() x 2;
x 2;
2) y = 3x + 1; 4) y = 0,4x + 3.
960.° Побудуйте графік функції:
1) y = 4 – x; 2) y = –4x + 5; 3) y = 0,2x – 3.
961.° Функцію задано формулою y = ![]() x. Знайдіть:
x. Знайдіть:
1) значення y, якщо x = 6; –3; –3,2;
2) значення x, при якому y = –2; ![]() ; 12.
; 12.
962.° Функцію задано формулою y = 0,6x. Заповніть таблицю:
|
x |
10 |
0,6 |
–5 |
–1,2 |
|
|
|
|
y |
|
|
|
|
4,8 |
–60 |
|
963.° Функцію задано формулою y = 1,2x. Знайдіть:
1) значення y, якщо x = 10; 0,6; –5; –4; 2) значення x, при якому y = 3,6; –2,4; 6.
964.° Побудуйте графік прямої пропорційності:
1) y = 3x; 3) y = –0,6x; 2) y = –2x; 4) y = ![]() x.
x.
965.° Побудуйте графік функції:
1) y = 5x; 2) y = 0,8x; 3) y ![]() x.
x.
966.° Функціональна залежність змінної y від змінної x є прямою пропорційністю.
1) Заповніть таблицю:
|
x |
8 |
6 |
2 |
1 |
|
0 |
–1 |
–2 |
–3 |
–4 |
|
y |
4 |
|
|
|
|
|
|
|
|
|
2) Задайте цю функцію формулою.3) Побудуйте графік цієї функції.
967.° Побудуйте в одній системі координат графіки лінійних функцій: y = 3; y = –5; y = 0.
968.° Побудуйте графік функції y = 2x – 3. Користуючись графіком, знайдіть:
1) значення функції, якщо значення аргументу дорівнює: 4; –1; 0,5; 2) значення аргументу, при якому значення функції дорівнює: 1; –1; 0;
3) значення аргументу, при яких функція набуває додатних значень.
969.° Побудуйте графік функції y = 2 – 4x. Користуючись графіком, знайдіть:
1) значення функції, якщо значення аргументу дорівнює: 1; 0; –2;
2) значення аргументу, при якому значення функції дорівнює: –4; –2; 2;
3) значення аргументу, при яких функція набуває від’ємних значень.
970.° Побудуйте графік функції y = 0,5x. Користуючись графіком, знайдіть:
1) значення функції, якщо значення аргументу дорівнює:
4; –6; 3;
2) значення аргументу, при якому значення функції дорівнює: 2,5; –2; 1;
3) значення аргументу, при яких функція набуває від’ємних значень.
971.° Побудуйте графік функції y = –4x. Користуючись графіком, знайдіть:
1) значення функції, якщо значення аргументу дорівнює: 2; –1; 0,5;
2) значення аргументу, при якому значення функції дорівнює: –4; 2;
3) значення аргументу, при яких функція набуває додатних значень.
972.° Не виконуючи побудови графіка функції y = 1,8x – 3, визначте, через які з даних точок проходить цей графік: A (–2; –6,6); B (1; 1,2); C (0; –3); D (5; 7).
973.° Не виконуючи побудови, визначте, чи належить графіку функції y = 8x – 14 точка: 1) A (–1; –6); 2) B (2; 2).
974.• Побудуйте в одній системі координат графіки функцій y x 1 і y ![]() x 2 та знайдіть координати точки їхнього перетину.
x 2 та знайдіть координати точки їхнього перетину.
975.• Побудуйте в одній системі координат графіки функцій y = = 5x – 6 і y = –2x + 1 та знайдіть координати точки їхнього перетину.
976.• Не виконуючи побудови, знайдіть координати точок перетину з осями координат графіка функції: 1) y = 2,5x + 10; 2) y = 6x – 4.
977.• Не виконуючи побудови, знайдіть координати точок перетину з осями координат графіка функції:
1) y ![]() x 4; 2) y = 7 – 3x.
x 4; 2) y = 7 – 3x.
978.• Не виконуючи побудови графіка функції y = 2x – 9, знайдіть точку цього графіка, у якої:
1) абсциса дорівнює ординаті; 2) ордината на 6 більша за абсцису.
979.• Не виконуючи побудови графіка функції y = –7x + 8, знайдіть точку цього графіка, абсциса та ордината якої — протилежні
числа.
980.• Не виконуючи побудови, знайдіть координати точок перетину графіків функцій:
1) y = 3,7x + 10 і y = 1,4x – 13;
2) y 4 ![]() x і y
x і y ![]() x 26.
x 26.
981.• Не виконуючи побудови, знайдіть координати точок перетину графіків функцій y = 4x – 7 і y = –2x + 11.
982.• При якому значенні змінної x функції f (x) = 4x – 3 і g (x) = = 3x – 2 набувають рівних значень? Побудуйте на одній координатній площині графіки функцій f і g. Визначте, при яких значеннях x:
1) f (x) > g (x); 2) f (x) < g (x).
983.• При якому значенні незалежної змінної функції f (x) = 5 – 2x і g (x) = 2x – 3 набувають рівних значень? Побудувавши на одній координатній площині графіки даних функцій, установіть, при яких значеннях x:
1) f (x) < g (x); 2) f (x) > g (x).
984.• Задайте формулою функцію, яка є прямою пропорційністю, якщо її графік проходить через точку M (2; –5).
985.• Знайдіть значення b, при якому графік функції y ![]() x b проходить через точку A (–27; 4).
x b проходить через точку A (–27; 4).
986.• При якому значенні k графік функції y = kx – 15 проходить через точку B (3; –6)?
987.• Графік функції y = kx + b перетинає осі координат у точках C (0; 4) і D (–8; 0). Знайдіть значення k і b.
988.• Графік функції y = kx + b перетинає осі координат у точках M (3; 0) і K (0; –1). Знайдіть значення k і b.
989.• Усі точки графіка функції y = kx + b мають однакову ординату, яка дорівнює –6. Знайдіть значення k і b.
990.• Графік функції y = kx + b паралельний осі абсцис і проходить через точку A (–2; 3). Знайдіть значення k і b.
991.• Один із графіків, наведених на рисунку 44, відображає процес наповнення водою першого бака, а другий — витікання води з другого бака.
1) Яким процесам відповідають графіки, наведені на рисунку 44?
2) Скільки води було спочатку в кожному баку?
3) Скільки води було в кожному баку через 2 хв після відкриття кранів? через 6 хв?
4) Через скільки хвилин після відкриття кранів у кожному баку було по 30 л води?
5) Скільки літрів води щохвилини наливається в перший бак і скільки виливається з другого?
6) Задайте формулою залежність кількості води в кожному баку від часу.
а б
Рис. 44
992. • Яка з прямих, зображених на рисунку 45, є графіком функції:
1) y = x; 3) y = ![]() x ;
x ;
2) y = 4x; 4) y ![]() x ?
x ?
993.• Яка з прямих, зображених на рисунку 46, є графіком функції:
1) y = –x; 3) y ![]() x ;
x ;
2) y = 3x; 4) y = –2x?
994.•• Задайте формулою які-небудь дві лінійні функції, графіки яких проходять через точку: 1) A (0; 4); 2) B (1; 3).
995.•• Графіки функцій y = 0,5x – 3, y = –4x + 6 і y = kx перетинаються в одній точці. Знайдіть значення k. Побудуйте в одній системі координат графіки цих функцій.
996.•• При якому значенні b графіки функцій y = 1,5x – 3, y = = 2,5x + 1 і y = 5x + b перетинаються в одній точці?
997.•• Точка C належить відрізку AB завдовжки 8. Довжина відрізка AC дорівнює x, довжина відрізка BC — y. Побудуйте графік залежності y від x, якщо 0 < x < 8. Позначте на цьому графіку точку, яка відповідає випадку, коли точка C — середина відрізка AB.
998.•• Периметр прямокутника ABCD дорівнює 12, AB = x, AD = y, 0 < x < 6. Побудуйте графік залежності y від x. Позначте на цьому графіку точку, яка відповідає випадку, коли прямокутник ABCD є квадратом.
999.•• Побудуйте графік функції:
x 4, якщо x l0, 2, якщо x 2,
1) y 3) y
2x 4, якщо x 0; 3, якщо x 2;
2x , якщо x 1,
3x 2, якщо x m1,
2) y 4) y 1, якщо x 1,
1, якщо x 1; x 3, якщо x 1.
1000.•• Побудуйте графік функції:
3x, якщо x m 1,
|
1) y 3, якщо 1 x 1, 2) y 2x 1, якщо x l1; 1001.•• Побудуйте графік функції: |
5 x , якщо x m3, x 1, якщо x 3. |
|
1) y = | x |; 2) y = | x | + x; 1002.•• Побудуйте графік функції: |
3) y = 4x – | x | + 2. |
|
1) y = –| x |; 2) y = x – | x |; |
3) y = 3x + 2 | x |. |
1003.* Задайте формулою лінійну функцію, графіком якої є зображена на рисунку 47: 1) пряма a; 2) пряма b.
1004.* Задайте формулою лінійну функцію, графіком якої є зображена на рисунку 48: 1) пряма m; 2) пряма n.
1005.* Функцію задано описом: значення функції дорівнює різниці між значенням аргументу й цілою частиною аргументу[11]. Побудуйте графік цієї функції.
Рис. 47 Рис. 48
![]()
1006. Троє друзів вирішили створити фірму з виробництва меблів і домовилися ділити прибуток пропорційно своїм внескам до статутного капіталу фірми. Один із них уніс 75 000 грн, другий — 125 000 грн, а третій — 175 000 грн. За підсумками першого року роботи прибуток склав 1 800 000 грн. Скільки грошей має отримати кожний з друзів?
1007. Знайдіть значення виразу:
1) (2 + 3a) (5 – a) – (2 – 3a) (5 + a) при a = –1,5;
2) (3a b)2 (3a b)2 при a 3![]() , b = 0,3.
, b = 0,3.
1008. Розв’яжіть рівняння:
1) (5x + 1) (2x – 3) = (10x – 9) (x + 2); 2) (7x – 1) (x + 5) = (3 + 7x) (x + 3).
1009. Доведіть, що сума кубів трьох послідовних натуральних чисел ділиться націло на 3.
1010. У двох діжках було порівну води. Об’єм води в першій діжці спочатку збільшили на 10 %, а потім зменшили на 10 %. Об’єм води в другій діжці, навпаки, спочатку зменшили на 10 %, а потім збільшили на 10 %. У якій діжці води стало більше?
1011. Відомо, що x2 + y2 = a, xy = b. Чому дорівнює значення виразу x4 + x2y2 + y4?
1012. Доведіть, що при будь-якому значенні x значення виразу | x | – x більше за відповідне значення виразу 2x – x2 – 2.
![]() ГОТУЄМОСЯ ДО ВИВЧЕННЯ НОВОЇ ТЕМИ
ГОТУЄМОСЯ ДО ВИВЧЕННЯ НОВОЇ ТЕМИ
1013. Знайдіть значення виразу:
1) 0,1x + 5y, якщо x = –4, y = 0,6;
2) x2 – 3y + 7, якщо x = 6, y = –2;
3) | x | + | y – 6 |, якщо x = –10, y = 2;
4) (2y – 3)2 – (x + 4)2, якщо x = –4, y = 1,5.
1014. Зобразіть на координатній площині всі точки (x; y) такі, що:
1) x = –3, y — довільне число; 2) y = 2, x — довільне число; 3) x = 0, y — довільне число.
 УЧИМОСЯ РОБИТИ НЕСТАНДАРТНІ КРОКИ
УЧИМОСЯ РОБИТИ НЕСТАНДАРТНІ КРОКИ
1015. Є два друкарських автомати. Перший, отримавши на вході картку із числами (a; b; c), видає на виході картку із числами a b; b c; a c , а другий за карткою із числами (a; b; c) —
2 2 2
картку із числами (2a – b; 2b – c; 2c – a). Чи можна за допомогою цих автоматів з картки із числами (2,8; –1,7; 16) отримати картку із числами (1,73; 2; 0,4)?
ЗАВДАННЯ № 6 «ПЕРЕВІРТЕ СЕБЕ» В ТЕСТОВІЙ ФОРМІ
1. При якому значенні аргументу значення функції y = –1,5x + 4 дорівнює –2?
А) 4; Б) –4; В) 2; Г) –2.
2. Серед наведених функцій укажіть пряму пропорційність:
А) y = 12 + x; В) y = 12;
x
Б) y = 12; Г) y = 12x.
3. Яка з даних функцій не є лінійною?
А) y = –2x + 9; В) y x 9;
2
Б) y 2 9; Г) y = 9 – 0,2x.
x
4. Через яку з даних точок проходить графік функції y = x2 – 3?
А) A (–3; 0); В) C (–3; 3); Б) B (–3; 6); Г) D (–3; –12).
5. Уранці учень пішов до школи, а після уроків повернувся додому. На рисунку 49 зображено графік залежності відстані між учнем та його домом від часу, який минув від моменту виходу з дому. Скільки годин учень перебував у школі?
А) 5 год; Б) 4,5 год; В) 4 год; Г) 3,5 год.
6. Графіком якої з даних функцій є пряма, що проходить через початок координат?
А) y = 20 + x; Б) y = 20x; В) y = 20 – x; Г) y = x – 20.
7. Графіком якої з даних функцій є горизонтальна пряма?
А) y = ![]() ; Б) y
; Б) y ![]() x ; В) y
x ; В) y ![]() x 1; Г) y =
x 1; Г) y = ![]() x .
x .
8. У якій точці графік функції y = x – 2 перетинає вісь ординат? А) A (0; –2); Б) B (0; 2); В) C (2; 0); Г) D (–2; 0).
9. Визначте абсцису точки перетину графіків функцій y = 8 – 4x і y = x + 14.
А) –2; Б) 2; В) –1,2; Г) 1,2.
завдання № 6 «Перевірте себе» в тестовій формі
![]()
10. На якому з рисунків зображено графік функції y = 0,2x (рис. 50)?
А) Б) В) Г)
11. ![]() Графік якої функції зображено на рисунку 51?
Графік якої функції зображено на рисунку 51?
А) y = 3x; В) y = x + 3;
Б) y = –x + 3; Г) y = ![]() x.
x.
12. При якому значенні m графік функції y = = mx + 2m – 5 перетинає вісь x у точці з абсцисою –1?
А) 5; Б) –5; В) –3; Г) 3.
ГОЛОВНЕ В ПАРАГРАФІ 3
Функція
Функцією називають правило, за допомогою якого за кожним значенням незалежної змінної можна знайти єдине значення залежної змінної.
Область визначення функції
Усі значення, яких набуває аргумент, утворюють область визначення функції.
Область значень функції
Усі значення, яких набуває залежна змінна, утворюють область значень функції.
Способи задання функції
За допомогою опису; за допомогою формули; табличний; графічний.
Графік функції
Графіком функції f називають геометричну фігуру, яка складається з усіх тих і тільки тих точок координатної площини, абсциси яких дорівнюють значенням аргументу, а ординати — відповідним значенням функції f.
Лінійна функція
Функцію, яку можна задати формулою виду y = kx + b, де k і b — деякі числа, x — незалежна змінна, називають лінійною.
Графік лінійної функції
Графіком лінійної функції є пряма.
Пряма пропорційність
Лінійну функцію, яку задають формулою y = kx, де k ≠ 0, називають прямою пропорційністю.
![]() § 4 СИСТЕМИ ЛІНІЙНИХ РІВНЯНЬ ІЗ ДВОМА ЗМІННИМИ
§ 4 СИСТЕМИ ЛІНІЙНИХ РІВНЯНЬ ІЗ ДВОМА ЗМІННИМИ
• У цьому параграфі ви ознайомитеся з рівняннями з двома змінними та їхніми системами. Вивчите деякі методи їхнього розв’язування.
• Ви дізнаєтеся, що рівняння з двома змінними може слугувати математичною моделлю реальної ситуації.
• оволодієте новим ефективним методом розв’язування текстових задач.
24. Рівняння з двома змінними
Розглянемо кілька прикладів реальних ситуацій.
ПРИКЛАД 1 Відстань між Києвом і Харковом дорівнює 450 км.
З Києва до Харкова зі швидкістю x км/год виїхав автомобіль. Через 1 год назустріч йому з Харкова зі швидкістю y км/год виїхав другий автомобіль. Вони зустрілися через 2 год після виїзду другого автомобіля.
Побудуємо математичну модель цієї ситуації.
Шлях, пройдений другим автомобілем до зустрічі, дорівнює 2y км. Оскільки перший автомобіль перебував у дорозі на 1 год більше, ніж другий, тобто 3 год, то до зустрічі він проїхав 3x км.
Разом автомобілі проїхали 450 км.
Звідси 3x 2y 450.
![]() Ця рівність із двома змінними є математичною моделлю описаної вище реальної ситуації.
Ця рівність із двома змінними є математичною моделлю описаної вище реальної ситуації. ¤
Розглянемо ще кілька прикладів ситуацій, математичними моделями яких є рівності з двома змінними.
![]() ПРИКЛАД 2 Площа квадрата, сторона якого — 10 см, дорівнює сумі площ двох інших квадратів.
ПРИКЛАД 2 Площа квадрата, сторона якого — 10 см, дорівнює сумі площ двох інших квадратів.
Площа квадрата зі стороною 10 см дорівнює 100 см2. Якщо довжини сторін двох інших квадратів позначити x см і y см, то отримаємо рівність
![]() x 2 y 2 100.
x 2 y 2 100. ¤
![]() ПРИКЛАД 3 Дано прямокутний трикутник.
ПРИКЛАД 3 Дано прямокутний трикутник.
Якщо градусні міри його гострих кутів позначити x і y, то можна записати:
![]() x y 90.
x y 90. ¤
![]()
![]() ПРИКЛАД 4 Дано прямокутник, площа якого дорівнює 12 см2. Позначимо довжини його сторін x см і y см. Тоді xy =12.
ПРИКЛАД 4 Дано прямокутник, площа якого дорівнює 12 см2. Позначимо довжини його сторін x см і y см. Тоді xy =12. ¤
![]() ПРИКЛАД 5 Купили 5 ручок і 7 зошитів. За всю покупку заплатили 19 грн.
ПРИКЛАД 5 Купили 5 ручок і 7 зошитів. За всю покупку заплатили 19 грн.
Якщо одна ручка коштує x грн, а один зошит — y грн, то можна записати:
![]() 5x + 7y = 19.
5x + 7y = 19. ¤
Як бачимо, кожна з отриманих у прикладах 1–5 рівностей
3x 2y 450, x 2 y 2 100, x y 90, xy =12,
5x + 7y = 19
містить по дві змінні x і y. Такі рівності називають рівняннями з двома змінними.
Якщо, наприклад, у рівняння xy =12 замість x і y підставити числа 2 і 6, то отримаємо правильну рівність 2æ6 =12. У такому разі говорять, що пара значень змінних x =2, y =6 задовольняє дане рівняння або що ця пара є розв’язком даного рівняння.
Означення. Пару значень змінних, яка перетворює рівняння в правильну рівність, називають розв’язком рівняння з двома змінними.
Так, для рівняння x 2 y 2 100 кожна з пар чисел x = 8, y =6;
x 6, y = 8;
x =10, y = 0
є його розв’язком, а, наприклад, пара x =5, y = 9 його розв’язком не є.
Звернемо увагу на те, що дане означення схоже на означення кореня рівняння з однією змінною. Через це виникає поширена помилка: кожне число пари або саму пару, що є розв’язком, називати коренем рівняння з двома змінними.
Той факт, що пара x = a, y = b є розв’язком рівняння, прийнято записувати так: (a; b) є розв’язком рівняння. У дужках на першому місці[12] пишуть значення змінної x, а на другому — значення змінної y.
Використовуючи таке позначення, можна, наприклад, записати, що кожна з пар чисел (5; 85), (40; 50), (50; 40) є розв’язком рівняння x + y = 90.
Три вказані пари чисел не вичерпують усі розв’язки цього рівняння. Якщо замість змінної y підставлятимемо в рівняння x + y = = 90 будь-які її значення, то матимемо лінійні рівняння з однією змінною, коренями яких є відповідні значення змінної x. Зрозуміло, що таким чином можна отримати безліч пар чисел, які є розв’яз- ками рівняння x y 90.
![]()
![]() Рівняння з двома змінними не обов’язково має безліч розв’язків. Наприклад, рівняння x y 0 має тільки один розв’язок — пару чисел (0; 0). Справді, оскільки x l0 і y l0, то при x ≠ 0 або y ≠ 0 ліва частина рівняння набуває тільки додатних значень. Рівняння x2 y2 2 взагалі не має розв’язків.
Рівняння з двома змінними не обов’язково має безліч розв’язків. Наприклад, рівняння x y 0 має тільки один розв’язок — пару чисел (0; 0). Справді, оскільки x l0 і y l0, то при x ≠ 0 або y ≠ 0 ліва частина рівняння набуває тільки додатних значень. Рівняння x2 y2 2 взагалі не має розв’язків.
Зауважимо, що ми розв’язали рівняння ![]() x 0 і x 2 y 2 2, але не розв’язали рівняння x + y = 90.
x 0 і x 2 y 2 2, але не розв’язали рівняння x + y = 90.
Означення. Розв’язати рівняння з двома змінними — це означає знайти всі його розв’язки або показати, що воно не має розв’язків.
Властивості рівнянь із двома змінними запам’ятати легко: вони аналогічні властивостям рівнянь з однією змінною, які ви вивчали в курсі математики 6 класу.
• Якщо до обох частин даного рівняння додати (або від обох частин відняти) одне й те саме число, то отримаємо рівняння, яке має ті самі розв’язки, що й дане.
• Якщо будь-який доданок перенести з однієї частини рівняння в другу, змінивши при цьому його знак на протилежний, то отримаємо рівняння, яке має ті самі розв’язки, що й дане.
• Якщо обидві частини рівняння помножити (поділити) на одне й те саме відмінне від нуля число, то отримаємо рівняння, яке має ті самі розв’язки, що й дане.
Розглянемо рівняння x 2 y 2 2 2x 2y. Перетворимо його, використовуючи властивості рівнянь. Маємо:
x 2 2x y 2 2y 2 0.
Далі запишемо: x2 – 2x + 1 + y2 + 2y + 1 = 0; (x – 1)2 + (y + 1)2 = 0.
Оскільки (x – 1)2 l 0 і (y + 1)2 l 0, то ліва частина рівняння перетворюється в нуль тільки при одночасному виконанні умов: x – 1 = 0 і y + 1 = 0. Звідси випливає, що пара чисел (1; –1) — єдиний розв’язок даного рівняння.
Вивчаючи якийсь об’єкт, ми прагнемо не тільки описати його властивості, а й скласти про нього наочне уявлення. Графік функції — характерний тому приклад. Оскільки розв’язком рівняння з двома змінними є пара чисел, наприклад (a; b), то цілком природно зобразити цей розв’язок у вигляді точки M (a; b) на координатній площині. Якщо зобразити всі розв’язки рівняння, то матимемо графік рівняння.
Означення. Графіком рівняння з двома змінними на-
зивають геометричну фігуру, що складається з усіх тих і тільки тих точок координатної площини, координати яких (пари чисел) є розв’язками даного рівняння.
Наприклад, розглянуте вище рівняння x2 + y2 + 2 = 2x – 2y має єдиний розв’язок (1; –1). Тому його графіком є єдина точка M (1; –1) (рис. 52).
На рисунку 53 зображено графік функції y = 2x – 1. Оскільки формула, яка задає лінійну функцію, є рівнянням із двома змінними, то також можна сказати, що на рисунку 53 зображено графік рівняння y = 2x – 1.
Наголосимо, що коли якась фігура є графіком рівняння, то виконуються дві умови:
1) усі розв’язки рівняння є координатами точок, які належать графіку;
2) координати будь-якої точки, що належить графіку, — це пара чисел, яка є розв’язком даного рівняння.

Рис. 52 Рис. 53
Рис. 54 Рис. 55
Графіки рівнянь є дуже різноманітними. З багатьма з них ви ознайомитеся в курсі алгебри пізніше. Наприклад, із курсу алгебри 8 класу ви дізнаєтеся, що графіком розглянутого на початку пункту рівняння xy =12 є фігура, зображена на рисунку 54. Її називають гіперболою. А в курсі геометрії 9 класу ви зможете довести, що графіком рівняння x 2 y 2 4 є коло (рис. 55).
![]() ПРИКЛАД 6 Побудуйте графік рівняння xy + 3y = 0.
ПРИКЛАД 6 Побудуйте графік рівняння xy + 3y = 0.
Розв’язання. Запишемо дане рівняння у вигляді y (x + 3) = 0. Звідси y = 0 або x + 3 = 0.
Отже, розв’язками даного рівняння є всі пари чисел виду (x; 0), де x — довільне число, і всі пари чисел виду (–3; y), де y — довільне число.
![]() Усі точки, координати яких мають вигляд (x; 0), де x — довільне число, утворюють вісь абсцис.
Усі точки, координати яких мають вигляд (x; 0), де x — довільне число, утворюють вісь абсцис.
Усі точки, координати яких мають вигляд (–3; y), де y — довільне число, утворюють пряму, яка проходить через точку (–3; 0) паралельно осі ординат.
Отже, графіком даного рівняння є пара
прямих, зображених на рисунку 56. ¤ Рис. 56
1. Що називають розв’язком рівняння з двома змінними?
2. Що означає розв’язати рівняння з двома змінними?
3. Сформулюйте властивості рівнянь із двома змінними.
4. Що називають графіком рівняння з двома змінними?
5. ![]() Чи може графік рівняння з двома змінними складатися тільки з однієї точки?
Чи може графік рівняння з двома змінними складатися тільки з однієї точки?
6. Яка фігура є графіком рівняння y = kx + b?
![]()
1016.° Які з даних рівнянь є рівняннями з двома змінними:
1) 2x + y = 8; 4) a 2 3b 8c; 7) x 3 8x 100;
2) x + y + z = 0; 5) xy + 1 = 2; 8) x 3 8y 100; 3) a 2 3b 8; 6) 5m – 3n = 6; 9) x 3 8xy 100?
1017.° Чи є пара чисел (–2; 3) розв’язком рівняння:
1) 4x + 3y = 1; 2) x2 + 5 = y2; 3) xy = 6?
1018.° Які з пар чисел (0; 1), (5; –4), (0; 1,2), (–1; 1), (1; –1) є розв’язками рівняння:
1) x2 + 5y – 6 = 0; 2) xy + x = 0?
1019.° Чи належить графіку рівняння 2x 2 y 1 0 точка:
1) A (–3; –17); 2) B (2; 9); 3) C (–2; 9); 4) D (–1; 4)?
1020.° Доведіть, що графік рівняння xy – 12 = 0 не проходить через точку:
1) A (3; –4); 2) B (–2; 6); 3) C (7; 2).
1021.° Чи проходить через початок координат графік рівняння:
1) 12x + 17y = 0; 2) x 2 xy 2 0; 3) x 3 4y y 2 3x ?
1022.° Укажіть які-небудь три розв’язки рівняння:
1) x – y = 10; 2) x = 4y; 3) 2x2 + y = 20.
1023.° Укажіть які-небудь три розв’язки рівняння:
1) x + y = 1; 2) 5x – y = 2.
1024.• Графік рівняння 4x + 3y = 30 проходить через точку A (6; b). Чому дорівнює значення b?
1025.• Графік рівняння 7x – 5y = 47 проходить через точку B (a; –1). Чому дорівнює значення a?
1026.• Не виконуючи побудови, знайдіть координати точок перетину з осями координат графіка рівняння:
1) x + y = 2; 2) x3 – y = 1; 3) x2 + y2 = 9; 4) | x | – y = 5.
1027.• Не виконуючи побудови, знайдіть координати точок перетину з осями координат графіка рівняння:
1) 2x – 3y = 6; 2) x2 + y = 4; 3) | x | + | y | = 7.
1028.• Складіть яке-небудь рівняння з двома змінними, розв’язком якого є пара чисел:
1) x = 1, y = 2; 2) x = –3, y = 5; 3) x = 10, y = 0.
1029.• Складіть яке-небудь рівняння з двома змінними, графік якого проходить через точку:
1) A (–2; 2); 2) B (4; –1); 3) C (0; 0).
1030.• Придумайте три рівняння, графіки яких проходять через точку M (6; –3).
1031.• Придумайте три рівняння, графіки яких проходять через точку K (0; 4).
1032.• Чи належать графіку рівняння x4 – y = –2 точки, що мають від’ємну ординату?
1033.• Чи проходить графік рівняння x + y2 = –4 через точки, що мають додатну абсцису?
1034.• Чи має розв’язки рівняння:
1) y 2 = x 2; 4) x 2 y 2 25; 7) | x | + | y | = 1; 2) y 2 x 2; 5) x 2 y 2 25; 8) | x | + | y | = 0;
3) xy = 0; 6) x 2 y 2 9; 9) | x | + | y | = –1?
У разі ствердної відповіді вкажіть які-небудь розв’язки.
1035.• Розв’яжіть рівняння:
1) x 2 y 2 0; 2) (x 2)2 (y 3)2 0; 3) x 4 y 6 4.
1036.• Скільки розв’язків має рівняння:
1) x 2 (y 2)2 0; 5) xy = 2;
2) (x + 3)2 + (y – 1)2 = 0; 6) | x + 1 | + | y | = 0;
3) ![]() 9x 2 16y 2 0; 7) x 2 y 100;
9x 2 16y 2 0; 7) x 2 y 100;
4) (x 2 y 2) y 0; 8) x + y = 2?
1037.• Наведіть приклад рівняння зі змінними x і y:
1) яке має один розв’язок;
2) яке не має розв’язків;
3) яке має безліч розв’язків;
4) розв’язком якого є будь-яка пара чисел.
1038.•• Що являє собою графік рівняння:
1) (x 1)2 (y 5)2 0; 3) 4x + y = y + 4x;
2) | x + 9 | + | y – 8 | = 0; 4) (x – 1) (y + 5) = 0?
1039.•• Побудуйте графік рівняння:
![]() 1) (x 2)2 y 2 0; 4) (x + 1) (y – 1) = 0; 2) x (y 3)2 0; 5) xy – 2y = 0.
1) (x 2)2 y 2 0; 4) (x + 1) (y – 1) = 0; 2) x (y 3)2 0; 5) xy – 2y = 0.
3) xy = 0;
1040.•• Побудуйте графік рівняння:
1) | x – 4 | + | y – 4 | = 0; 2) (x – 4) (y – 4) = 0; 3) xy + x = 0.
1041.•• Знайдіть усі пари (x; y) натуральних чисел, які є розв’язками рівняння:
1) 2x + 3y = 5; 2) x + 5y = 16.
1042.•• Знайдіть усі пари (x; y) цілих чисел, які є розв’язками рівняння | x | + | y | = 2.
1043.•• Знайдіть усі пари (x; y) цілих чисел, які є розв’язками рівняння x2 + y2 = 5.

Рис. 57 Рис. 58
1044.•• Катерині треба заплатити за математичний довідник 29 грн. У неї є купюри тільки по 2 грн і по 5 грн. Скількома способами вона може розрахуватися за покупку без здачі?
1045.•• Учням і ученицям 7 класу на конкурсі з математики було запропоновано задачі з алгебри та з геометрії. За кожну правильно розв’язану задачу з алгебри нараховували 2 бали, а за задачу з геометрії — 3 бали. Максимальна кількість набраних балів могла скласти 24. Скільки було запропоновано задач окремо з алгебри та з геометрії, якщо з кожного із цих предметів була хоча б одна задача? Знайдіть усі можливі відповіді.
1046.•• Розв’яжіть рівняння:
1) x 2 y 2 4 4y; 3) x 2 y 2 x y 0,5 0; 2) x 2 y 2 2x 6y 10 0; 4) 9x 2 y 2 2 6x .
1047.•• Розв’яжіть рівняння:
1) x2 + 10y + 30 = 10x – y2 – 20; 2) 4x2 + y2 + 4x = 2y – 3.
1048.•• Графіком рівняння (x2 + y2 + y)2 = x2 + y2 є крива, яку нази вають кардіоїдою (рис. 57). Знайдіть координати точок її перетину з осями координат.
1049.•• Графіком рівняння x 2 y2 1 є крива, яку називають еліп-
25 16
сом (рис. 58). Знайдіть координати точок її перетину з осями координат.
![]()
1050. У посудину, яка містить 150 мл 8 %-го розчину кислоти, додали 90 мл води. Чому дорівнює концентрація кислоти в одержаному розчині?
1051. У мішку 7 червоних, 10 зелених і 12 жовтих яблук. Яку найменшу кількість яблук треба вийняти, не заглядаючи в мішок, щоб із ймовірністю, яка дорівнює 1, серед вийнятих яблук хоча б одне було зеленим?
1052. Знайдіть корінь рівняння:
1) ![]() x 4; 2)
x 4; 2) ![]() x 9.
x 9.
1053. З міста A до міста B одночасно виїхали легковий і вантажний автомобілі. Через 3,5 год після виїзду легковий автомобіль прибув у місто B, а вантажному залишилося ще проїхати 77 км. Знайдіть відстань між містами, якщо швидкість вантажного автомобіля в 1,4 раза менша від швидкості легкового.
1054. Чи можна стверджувати, що при будь-якому натуральному парному значенні n значення виразу (5n + 10)2 – (2n + 4)2 ділиться націло на 84?
1055. Відомо, що при деяких значеннях m, n і k значення виразу 3m2n дорівнює 2, а значення виразу n2k4 дорівнює 3. Знайдіть при тих самих значеннях m, n і k значення виразу:
1) (3m2n2k2)2; 2) (–2m2nk2)3æ(0,5n2k)2.
![]() УЧИМОСЯ РОБИТИ НЕСТАНДАРТНІ КРОКИ
УЧИМОСЯ РОБИТИ НЕСТАНДАРТНІ КРОКИ
1056. Порівняйте значення виразів (1æ2æ3æ...æ999æ1000)2 і 10001000.
![]() 25. Лінійне рівняння з двома змінними та його графік
25. Лінійне рівняння з двома змінними та його графік
Означення. Лінійним рівнянням із двома змінними називають рівняння виду ax + by = c, де x і y — змінні, a, b, c — деякі числа.
Рівняння 3x + 2y = 450, x + y = 90, які розглядалися в попередньому пункті, є лінійними. Ось ще приклади лінійних рівнянь: x + y = 3; 0x + 5y = –1; –3x + 0y = 5; 0x + 0y = 0; 0x + 0y = 2.
З’ясуємо, яка фігура є графіком лінійного рівняння. Для цього розглянемо три випадки.
Випадок 1. Нехай задано лінійне рівняння ax + by = c, у якому b ≠ 0. Це рівняння можна перетворити так: by = –ax + c.
Оскільки b ≠ 0, то, поділивши обидві частини останнього рівняння на b, отримаємо:
y a x c. b b
a ![]() k, c = p. ТеВведемо позначення:
k, c = p. ТеВведемо позначення:
b b
пер можна записати:
y kx p.
Ми отримали формулу, яка задає лінійну функцію. Графіком лінійної функції є невертикальна пряма. Отже, графіком
Рис. 59 рівняння ax by c, де b ≠ 0, є невертикальна пряма.
![]() ПРИКЛАД 1 Побудуйте графік рівняння x 3y 2.
ПРИКЛАД 1 Побудуйте графік рівняння x 3y 2.
![]() Розв’язання. Ми вже знаємо, що графіком цього рівняння є пряма. Тому для побудови достатньо визначити координати двох будь-яких її точок. Маємо: якщо x =1, то y =1; якщо x 2, то y = 0. Тепер через точки M (1;1) і N (−2; 0) проведемо пряму (рис. 59). Ця пряма і є шуканим графіком.
Розв’язання. Ми вже знаємо, що графіком цього рівняння є пряма. Тому для побудови достатньо визначити координати двох будь-яких її точок. Маємо: якщо x =1, то y =1; якщо x 2, то y = 0. Тепер через точки M (1;1) і N (−2; 0) проведемо пряму (рис. 59). Ця пряма і є шуканим графіком. ¤
Випадок 2. Нехай задано лінійне рівняння ax by c, де a ≠ 0, b = 0. Отримуємо ax 0y c. Побудову графіка рівняння такого
виду розглянемо в прикладі 2.
![]() ПРИКЛАД 2 Побудуйте графік рівняння 3x 0y 6.
ПРИКЛАД 2 Побудуйте графік рівняння 3x 0y 6.
Розв’язання. Легко знайти кілька розв’язків цього рівняння. Ось, наприклад, чотири його розв’язки: (2; –1); (2; 0); 2; ![]() ;
;
![]() (2; –100). Зрозуміло, що будь-яка пара виду (2; t), де t — довільне число, є розв’язком рівняння 3x 0y 6. Отже, шуканий графік містить усі точки, абсциса кожної з яких дорівнює 2, а ордината — будь-яке число. Усі ці точки належать прямій, яка перпендикулярна до осі абсцис і проходить через точку (2; 0) (рис. 60). При цьому координати будь-якої точки цієї прямої — пара чисел, що є розв’язком даного рівняння. Отже, зазначена вертикальна пряма є шуканим графіком.
(2; –100). Зрозуміло, що будь-яка пара виду (2; t), де t — довільне число, є розв’язком рівняння 3x 0y 6. Отже, шуканий графік містить усі точки, абсциса кожної з яких дорівнює 2, а ордината — будь-яке число. Усі ці точки належать прямій, яка перпендикулярна до осі абсцис і проходить через точку (2; 0) (рис. 60). При цьому координати будь-якої точки цієї прямої — пара чисел, що є розв’язком даного рівняння. Отже, зазначена вертикальна пряма є шуканим графіком. ¤
![]() Міркуючи аналогічно, можна показати, що графіком рівняння ax + 0y = c, де a ≠ 0, є вертикальна пряма.
Міркуючи аналогічно, можна показати, що графіком рівняння ax + 0y = c, де a ≠ 0, є вертикальна пряма.
Тепер можна зробити такий висновок: у кожному з двох випадків: 1) b ≠ 0; 2) b = 0 і a ≠ 0 —графіком рівняння ax + by =c є пряма.
Часто, наприклад, замість речення «дано рів- няння y = 2x» говорять: «дано пряму y = 2x». Рис. 60 Випадок 3. Нехай дано лінійне рівняння ax + by = c, у якому a = b = 0. Маємо: 0x 0y c.
Якщо c ≠ 0, то це рівняння не має розв’язків, а отже, на координатній площині не існує точок, які могли б слугувати графіком рівняння.
Якщо c = 0, то рівняння набуває вигляду
0x 0y 0.
Будь-яка пара чисел є його розв’язком. Отже, у цьому випадку графіком рівняння є вся координатна площина.
У таблиці підсумовано матеріал, розглянутий у цьому пункті.
|
Рівняння |
Значення a, b, c |
Графік |
|
ax + by = c |
b ≠ 0, a і c — будь-які |
Невертикальна пряма |
|
ax + by = c |
b = 0, a ≠ 0, c — будь-яке |
Вертикальна пряма |
|
ax + by = c |
a = b = c = 0 |
Уся координатна площина |
|
ax + by = c |
a = b = 0, c ≠ 0 |
— |
![]() ПРИКЛАД 3 Виразіть із рівняння 3x – 2y = 6 змінну x через змінну y та знайдіть будь-які два розв’язки цього рівняння. Розв’язання. Маємо: 3x = 2y + 6;
ПРИКЛАД 3 Виразіть із рівняння 3x – 2y = 6 змінну x через змінну y та знайдіть будь-які два розв’язки цього рівняння. Розв’язання. Маємо: 3x = 2y + 6;
x ![]() ;
;
x ![]() y 2.
y 2.
Надаючи змінній y довільних значень та обчислюючи за отриманою формулою x ![]() y 2 відповідні значення змінної x, можемо знайти безліч розв’язків даного рівняння 3x – 2y = 6. Наприклад, якщо y = 6, то x
y 2 відповідні значення змінної x, можемо знайти безліч розв’язків даного рівняння 3x – 2y = 6. Наприклад, якщо y = 6, то x ![]() æ6 2 6; якщо y = –2, то x
æ6 2 6; якщо y = –2, то x ![]() æ( 2) 2
æ( 2) 2 ![]() .
.
![]() Пари чисел (6; 6) і
Пари чисел (6; 6) і ![]() ; 2 є розв’язками даного рівняння.
; 2 є розв’язками даного рівняння. ¤
![]() ПРИКЛАД 4 Складіть лінійне рівняння з двома змінними, графіком якого є пряма, що проходить через початок координат і точ- ку A (3; –12). Побудуйте графік цього рівняння.
ПРИКЛАД 4 Складіть лінійне рівняння з двома змінними, графіком якого є пряма, що проходить через початок координат і точ- ку A (3; –12). Побудуйте графік цього рівняння.
![]() Розв’язання. Оскільки графік шуканого рівняння проходить через точки O (0; 0) та A (3; –12), що мають різні абсциси, то він є невертикальною прямою. Тоді рівняння цієї прямої можна записати у вигляді y = kx + b, де k і b — деякі числа.
Розв’язання. Оскільки графік шуканого рівняння проходить через точки O (0; 0) та A (3; –12), що мають різні абсциси, то він є невертикальною прямою. Тоді рівняння цієї прямої можна записати у вигляді y = kx + b, де k і b — деякі числа.
З того, що графік проходить через початок координат, випливає, що b = 0. Оскільки графік проходить через точку A (3; –12), то –12 = kæ3, звідки k = –4.
Отже, шукане рівняння має вигляд y = –4x
Рис. 61 або 4x + y = 0. Графік цього рівняння зображено на рисунку 61. Відповідь: 4x + y = 0. ¤
1. Яке рівняння називають лінійним рівнянням із двома змінними?
2. ![]() Що є графіком рівняння ax+ by = c, коли b ≠ 0 або коли b = 0 і a ≠ 0?
Що є графіком рівняння ax+ by = c, коли b ≠ 0 або коли b = 0 і a ≠ 0?
3. Що є графіком рівняння ax + by = c при a = b = c = 0?
4. При яких значеннях a, b і c рівняння ax + by = c не має розв’язків?
ВПРАВИ
1057.° Чи є лінійним рівняння з двома змінними:
1) 7x + 11y = 36; 3) 12x – 17y = 0; 2) x2 + 4y = 6; 4) –3x + xy = 10?
1058.° Чи є лінійним рівняння з двома змінними:
1) 8x 0 9, y ![]() ; 3) 6x + 2xy = 9;
; 3) 6x + 2xy = 9;
2) x – 4y2 = 5; 4) 3x + 4y = 0?
1059.° Які з пар чисел (7; 1), (0; –2), (8; 2), (–7; –5), (10; 3) є розв’язками рівняння 3x – 7y = 14?
1060.° Розв’язком якого з рівнянь є пара чисел (3; –2):
1) 4x + 5y = 2; 2) 3x – 2y = 5; 3) 0,2x – 0,5y = 1,6? 1061.°Чи є розв’язком рівняння 2x – 9y = 13 пара чисел:
1) (2,5; 2); 2) (10,5; 2); 3) 5; ![]() ; 4) (–7; –3)?
; 4) (–7; –3)?
1062.° Відомо, що пара чисел (–5; y) є розв’язком рівняння 2x + 9y = 17. Знайдіть значення y.
1063.° Відомо, що пара чисел (–8; y) є розв’язком рівняння 2x – 3y = = 4. Знайдіть значення y.
1064.° Відомо, що пара чисел x; ![]() є розв’язком рівняння
є розв’язком рівняння ![]() x 6y 1.
x 6y 1.
Знайдіть значення x.
1065.° Відомо, що пара чисел (x; 6) є розв’язком рівняння 8x – 3y = 22. Знайдіть значення x.
1066.° Графіку якого з рівнянь належить точка M (1; 4):
1) 4y – 2x = –4; 2) 6x + 11y = 50?
1067.° Чи проходить графік рівняння 3x + y = –1 через точку:
1) M (–3; 10); 2) N (4; –13); 3) K (0; –1)?
1068.° Виразіть із даного рівняння змінну x через змінну y і знайдіть які-небудь три розв’язки цього рівняння:
1) x + y = 12; 3) x + 6y = 10; 5) –6x + 5y = 18; 2) x – 7y = 5; 4) 2x + 8y = 16; 6) 3x – 7y = 1.
1069.° Виразіть із даного рівняння змінну y через змінну x і знайдіть які-небудь два розв’язки цього рівняння:
1) 4x – y = 7; 2) –2x + y = 11; 3) 5x – 3y = 15.
1070.° Знайдіть які-небудь три розв’язки рівняння:
1) x – y = 10; 2) 2y – 5x = 11.
1071.° Знайдіть які-небудь три розв’язки рівняння:
1) 6x + y = 7; 2) 2x – 3y = –4.
1072.° Побудуйте графік рівняння:
1) x – y = 4; 3) x – 5y = 5; 5) 7x – 3y = 21; 2) 4x + y = 3; 4) 3x + 2y = 6; 6) 0 2, x ![]() y 1.
y 1.
|
1073.° Побудуйте графік рівняння: |
|
|
1) x + y = –3; 2) 6x + y = 0; |
3) 2x – 3y = 9. |
1074.° Які пари чисел є розв’язками рівняння:
1) 0x + 4y = 20; 2) –3x + 0y = 27?
1075.° Побудуйте графік рівняння:
1) 4y = –8; 2) 1,2x = 3,6.
1076.° Побудуйте графік рівняння:
1) –0,2x = 1; 2) 0,5y = 2.
1077.° У якій точці пряма 7y – 3x = 21 перетинає: 1) вісь x; 2) вісь y?
1078.° Знайдіть координати точок перетину прямої 0,3x + 0,2y = 6 з осями координат.
1079.° Складіть яке-небудь лінійне рівняння з двома змінними, розв’язком якого є пара чисел (–2; 1).
1080.° Складіть яке-небудь лінійне рівняння з двома змінними, розв’язком якого є пара чисел (3; 5).
1081.• Знайдіть розв’язок рівняння 7x + 8y = 30, який складається з двох рівних чисел.
1082.• Знайдіть розв’язок рівняння –12x + 17y = –87, який складається з двох протилежних чисел.
1083.• При якому значенні a пара чисел (a; 2a) є розв’язком рівняння 2x + 7y = 16?
1084.• При якому значенні a пара чисел (–4; 2) є розв’язком рівняння:
1) 3x + 5y = a; 2) ax + 5y = 18?
1085.• При якому значенні a графік рівняння 11x – 13y = a + 4 проходить через початок координат?
1086.• При якому значенні a через точку A (5; –3) проходить графік рівняння:
1) 4x – 9y = a; 2) 6x – ay = 15?
1087.• При якому значенні a графік рівняння ax + 4y = 0 проходить через точку:
1) A (12; –4); 2) B (0; 2); 3) O (0; 0)?
1088.• При якому значенні b графік рівняння 5x + by = 0 проходить через точку:
1) M (–4; –10); 2) N (0; 1); 3) K (–2; 0)?
1089.• Графіком яких з даних рівнянь є та сама пряма, що й графік рівняння 2x – 5y = 3:
1) 4x – 10y = 6; 3) 2x – 5y = 6; 5) x – 2,5y = 1,5; 2) 4x – 10y = 3; 4) 5y – 2x = –3; 6) –0,4x – y = 0,6?
1090.• Складіть рівняння з двома змінними за такою умовою:
1) довжина прямокутника дорівнює x м, ширина — y м, периметр — 18 м;
2) автобус їхав 4 год зі швидкістю x км/год і 3 год зі швидкістю y км/год, проїхавши всього 250 км;
3) зошит коштує x грн, а ручка — y грн, 2 ручки дорожчі за 5 зошитів на 1,2 грн;
4) кусок сплаву масою x кг, який містив 12 % міді, та кусок сплаву масою y кг, який містив 20 % міді, сплавили разом і отримали новий сплав, що містить 9 кг міді;
5) в одному ящику було x кг цукерок, а в другому — y кг; після того як із першого ящика переклали в другий 8 кг цукерок, в обох ящиках цукерок стало порівну.
1091.• Складіть рівняння з двома змінними за такою умовою:
1) бічна сторона рівнобедреного трикутника дорівнює a см, основа — b см, периметр — 32 см;
2) один автомобіль проїхав зі швидкістю x км/год за 6 год на 32 км менше, ніж другий автомобіль зі швидкістю y км/год за 7 год;
3) в одному магазині було x ц яблук, а в другому — y ц; за день у першому магазині продали 14 % яблук, а в другому — 18 % яблук, причому в другому магазині продали на 1,2 ц яблук менше, ніж у першому.
1092.• Доведіть, що прямі 5y – x = 6 і 3x – 7y = 6 перетинаються в точці A (9; 3).
1093.• Доведіть, що прямі 4x – 3y = 12 і 3x + 4y = –66 перетинаються в точці B (–6; –12).
1094.• Складіть лінійне рівняння з двома змінними, графіком якого є пряма, що проходить через початок координат і точку:
1) A (2; 8); 2) B (–6; 15).
1095.• Складіть лінійне рівняння з двома змінними, графіком якого є пряма, що проходить через початок координат і точку C (8; –12).
1096.• Доведіть, що не існує такого значення a, при якому пряма ax – 3y = 12 проходить через початок координат.
1097.• При якому значенні a точка перетину прямих 2x – 3y = –6 і 4x + y = a належить осі абсцис?
1098.• При якому значенні b точка перетину прямих 9x + 7y = 35 і x + by = –20 належить осі ординат?
1099.• При яких значеннях a і b пряма ax + by = 24 перетинає осі координат у точках A (–6; 0) і B (0; 12)?
1100.• На якому з рисунків 62, а–г зображено графік рівняння x + y = 3?
1101.• На якому з рисунків 63, а–г зображено графік рівняння x – y = –5?
Рис. 63
![]() 1102.• Яка з прямих, зображених на рисунку 64, є графіком рівняння: 1) 0x + y = –3; 3) 3x + 0y = 6; 2) 2x – y = 1; 4) x + 2y = 0?
1102.• Яка з прямих, зображених на рисунку 64, є графіком рівняння: 1) 0x + y = –3; 3) 3x + 0y = 6; 2) 2x – y = 1; 4) x + 2y = 0?
1103.• Чи належить графіку рівняння
13x + 17y = –40
хоча б одна точка, обидві координати якої — додатні числа?
1104.• Чи належить графіку рівняння
4x – 8y = 7
хоча б одна точка, обидві координати Рис. 64 якої — цілі числа?
1105.•• Складіть лінійне рівняння з двома змінними, графік якого перетинає осі координат у точках:
1) A (–4; 0) і B (0; 2); 2) C (0; –3) і D (5; 0).
1106.•• Складіть лінійне рівняння з двома змінними, графік якого проходить через точки M (6; 0) і K (0; 6).
1107.•• Складіть рівняння, графіки яких зображено на рисунку 65.
Рис. 65 Рис. 66
1108.•• Складіть рівняння, графіки яких зображено на рисунку 66.
1109.* Скільки існує пар простих чисел (x; y), які є розв’язками рівняння 5x – 6y = 3?
![]()
¿ 1110. Петру Івановичу треба купити 2 буханці хліба, 800 г ковбаси та 0,5 кг шинки. У таблиці наведено ціни на ці продукти в трьох магазинах, найближчих до дому Петра Івановича.
|
Магазин |
Ціна, грн |
|
|
|
Хліб (за буханець) |
Ковбаса (за 1 кг) |
Шинка (за 1 кг) |
|
|
«Смачно» |
13 |
140 |
200 |
|
«Апетит» |
12 |
135 |
180 |
|
«Свіжі продукти» |
14 |
155 |
240 |
У магазині «Смачно» у Петра Івановича є дисконтна картка зі знижкою в розмірі 5 % на всі продукти. У магазині «Свіжі продукти» цього дня діє знижка в розмірі 10 % на всі ковбасні та м’ясні вироби. У якому магазині Петру Івановичу найвигідніше зробити покупку?
1111. Дві бригади виготовили 840 деталей, причому одна бригада виготовила на 80 % більше деталей, ніж друга. Скільки деталей виготовила кожна бригада?
1112. Відомо, що 4 однакових екскаватори можуть вирити котлован за 12 год. За який час 6 таких самих екскаваторів вириють 3 таких котловани?
1113. Доведіть, що значення виразу 236 + 4100 – 232 – 498 кратне числу: 1) 15; 2) 240.
1114. Розв’яжіть рівняння:
1) (x 8)2 (x 4) (x 4) 0; 2) (4x 5) (4x 5) (4x 1)2 9 2x.
1115. Розкладіть на множники:
1) 6x 3 8x 2 3xy 4y; 3) 125x 3 − m 6n 9 ;
27 64
2) x4 – 6x2y + 9y2 – 16; 4) c2 – 2c – b2 – 4b – 3.
![]() ГОТУЄМОСЯ ДО ВИВЧЕННЯ НОВОЇ ТЕМИ
ГОТУЄМОСЯ ДО ВИВЧЕННЯ НОВОЇ ТЕМИ
1116. Яка з пар чисел (3; 3), (–3; 3), (–3, –3) є розв’язком кожного з рівнянь x2 + y2 = 18 і x + y = 0?
1117. ![]() На рисунку 67 зображено графіки рівнянь y = x2 і x – y + 2 = 0. Користуючись цим рисунком, знайдіть усі пари чисел, які є розв’язками кожного з даних рівнянь.
На рисунку 67 зображено графіки рівнянь y = x2 і x – y + 2 = 0. Користуючись цим рисунком, знайдіть усі пари чисел, які є розв’язками кожного з даних рівнянь.
УЧИМОСЯ РОБИТИ НЕСТАНДАРТНІ КРОКИ Рис. 67
1118. Сума 100 різних натуральних чисел дорівнює 5051. Знайдіть ці числа.
 Як будували міст між геометрією та алгеброю
Як будували міст між геометрією та алгеброю
Ідея координат зародилася дуже давно. Адже ще в давнину люди вивчали Землю, спостерігали зорі, а за результатами своїх досліджень складали карти, схеми.
У ІІ ст. до н. е. давньогрецький учений Гіппарх уперше використав ідею координат для визначення місця розташування об’єктів на поверхні Землі.
Лише в ХІV ст. французький учений Ніколя Орем (бл. 1323– 1392) уперше застосував у математиці ідею Гіппарха: він розбив площину на клітинки (подібно до того, як на клітинки поділено аркуш вашого зошита) і став задавати положення точок широтою та довготою.
Однак величезні можливості застосування цієї ідеї розкрили лише в ХVІІ ст. видатні французькі математики П’єр Ферма та Рене Декарт. У своїх працях ці вчені показали, як завдяки системі координат можна переходити від точок до чисел, від ліній — до рівнянь, від геометрії — до алгебри.

П’єр Ферма Рене Декарт
(1601–1665) (1596–1650)
Незважаючи на те що П. Ферма опублікував свою працю на рік раніше, ніж Р. Декарт, ту систему координат, якою дотепер користуються математики, назвали декартовою. Це пов’язано з тим, що Р. Декарт у праці «Міркування про метод» винайшов нову зручну буквену символіку, яку з невеликими змінами ми використовуємо й сьогодні. Слідом за ним ми позначаємо змінні останніми буквами латинського алфавіту x, y, z, а коефіцієнти — першими: a, b, c, ... . Звичні для нас позначення степенів x2, x3, y5 і т. ін. також увів Р. Декарт.
![]() 26. Системи рівнянь із двома змінними. Графічний метод розв’язування системи двох лінійних рівнянь із двома змінними
26. Системи рівнянь із двома змінними. Графічний метод розв’язування системи двох лінійних рівнянь із двома змінними
Легко перевірити, що пара чисел (–2; 0) є розв’язком як рівняння x2 + y2 = 4, так і рівняння y = x2 – 4. У таких випадках говорять, що пара чисел (–2; 0) — спільний розв’язок зазначених рівнянь.
На рисунку 68 зображено графіки рівнянь –6x + 5y = 9 і 4x + 3y = 13. Вони перетинаються в точці M (1; 3). Ця точка належить кожному з графіків. Отже, пара чисел (1; 3) є спільним розв’язком даних рівнянь.
Якщо поставлено завдання знайти сторони прямокутника, площа якого дорівнює 12 cм2, а периметр — 14 см, то треба знайти спільний розв’язок рівнянь xy =12 і 2x 2y 14, де x см і y см — довжини сусідніх сторін прямокутника.
Якщо треба знайти всі спільні розв’язки кількох рівнянь, то говорять, що треба розв’язати систему рівнянь.
Систему рівнянь записують за допомогою фігурної дужки. Так, запис
xy 12, 2x 2y 14
![]() є математичною моделлю задачі про знаходження сторін прямокутника, площа якого дорівнює 12 cм2, а периметр — 14 см. Система
є математичною моделлю задачі про знаходження сторін прямокутника, площа якого дорівнює 12 cм2, а периметр — 14 см. Система
6x 5y 9,
4x 3y 13
є математичною моделлю задачі про знаходження координат спільних точок двох прямих (рис. 68).
Обидва рівняння даної системи є лінійними. Тому цю систему називають системою двох лінійних рівнянь із двома
змінними. Рис. 68
Означення. Розв’язком системи рівнянь із двома змінними називають пару значень змінних, яка перетворює кожне рівняння системи в правильну рівність.
Із прикладу, наведеного на початку пункту, випливає, що пара чисел (–2; 0) є розв’язком системи рівнянь
x 2 y 2 4, y x 2 4.
Проте це зовсім не означає, що дану систему розв’язано.
Означення. Розв’язати систему рівнянь — це означає знайти всі її розв’язки або довести, що розв’язків немає.
Пара чисел (–2; 0) не вичерпує всіх розв’язків останньої системи. Наприклад, пара чисел (2; 0) — також її розв’язок. Цю систему, як і систему, отриману в задачі про прямокутник, ви навчитеся розв’язувати в курсі алгебри 9 класу.
А от систему рівнянь x 2 y 2 4,
y x 2 4
ми можемо розв’язати вже зараз. Очевидно, що перше рівняння цієї системи розв’язків не має, а отже, не існує і спільних розв’язків рівнянь, що входять до системи. Звідси можна зробити висновок:
дана система розв’язків не має.
Так само можна вважати розв’язаною систему рівнянь
6x 5y 9,
4x 3y 13.
Справді, графіки рівнянь системи перетинаються в точці M (1; 3) (рис. 68). Її координати є розв’язком кожного рівняння системи, а отже, і самої системи. Інших спільних точок графіки рівнянь не мають, таким чином, не має інших розв’язків і сама система. Висновок: пара чисел (1; 3) — єдиний розв’язок даної системи.
Описаний метод розв’язування системи рівнянь називають графічним. Його суть полягає в такому:
• побудувати на одній координатній площині графіки рівнянь, що входять до системи;
• знайти координати всіх точок перетину побудованих графіків;
• отримані пари чисел і будуть шуканими розв’язками.
Не будь-яку систему рівнянь доцільно розв’язувати графічно. Наприклад, якщо пара чисел ![]() ;
; ![]() є розв’язком якоїсь системи, то зрозуміло, що графічно встановити цей факт украй складно. А тому графічний метод зазвичай застосовують тоді, коли розв’язок достатньо знайти наближено. Те, що пара чисел (1; 3) є розв’язком
є розв’язком якоїсь системи, то зрозуміло, що графічно встановити цей факт украй складно. А тому графічний метод зазвичай застосовують тоді, коли розв’язок достатньо знайти наближено. Те, що пара чисел (1; 3) є розв’язком
6x 5y 9, системи підтверджує безпосередня підстановка цієї 4x 3y 13,
пари в кожне з рівнянь системи, тобто перевірка.
![]() Графічний метод є ефективним і тоді, коли треба визначити кількість розв’язків системи. Наприклад, на рисунку 69 зображено графіки деяких функцій y = f (x) і y = g (x). Ці графіки мають три спільні точки. Це дозволяє нам стверджувати, що y f (x),
Графічний метод є ефективним і тоді, коли треба визначити кількість розв’язків системи. Наприклад, на рисунку 69 зображено графіки деяких функцій y = f (x) і y = g (x). Ці графіки мають три спільні точки. Це дозволяє нам стверджувати, що y f (x),
система має три розв’язки.
y g (x)
З’ясуємо, скільки розв’язків може мати система двох лінійних рівнянь із двома Рис. 69 змінними.
Якщо одне з рівнянь системи не має розв’язків, то очевидно, що вся система розв’язків не має.
0x 0y 7,
Наприклад, система розв’язків не має.
2x 3y 15
Розглянемо випадок, коли кожне з рівнянь системи має розв’язки.
Якщо графіком одного з рівнянь системи є площина, то очевидно, що система має безліч розв’язків. Справді, площина та проведена на ній пряма мають безліч спільних точок.
0x 0y 0,
Наприклад, система має безліч розв’язків.
2x 3y 15
Якщо графіками рівнянь, що входять до системи лінійних рівнянь, є прямі, то кількість розв’язків цієї системи залежить від взаємного розміщення двох прямих на площині:
1) якщо прямі перетинаються, то система має єдиний розв’язок;
2) якщо прямі збігаються, то система має безліч розв’язків; 3) якщо прямі паралельні, то система розв’язків не має.
Приклад, який відповідає випадку, коли система має єдиний
6x 5y 9,
розв’язок, ми вже розглянули вище. Це система
4x 3y 13.
Тепер звернемося до прикладів, що ілюструють випадки 2 і 3. Так, якщо в системі
x y 1,
2
x 2y 2
обидві частини першого рівняння помножити на 2, то розв’язки цього рівняння, а отже, і всієї системи не зміняться. Маємо:
x 2y 2, x 2y 2.
Очевидно, що розв’язки цієї системи збігаються з розв’язками рівняння x – 2y = 2. Проте це рівняння має безліч розв’язків, отже, і розглядувана система також має безліч розв’язків. Наведемо приклад системи, яка не має розв’язків:
![]() x y 2,
x y 2,
2x 3y 7.
Справді, помножимо обидві частини першого рівняння системи на 3. Отримаємо:
2x 3y 6, 2x 3y 7.
Зрозуміло, що не існує такої пари значень x і y, при яких вираз 2x + 3y одночасно набуває значення і 6, і 7.
На закінчення зазначимо, що саме графічний метод нам підказав, що не існує системи лінійних рівнянь, яка мала б, наприклад, рівно два, або рівно три, або рівно 100 й т. п. розв’язків.
1. У якому випадку говорять, що треба розв’язати систему рівнянь?
2. Що є розв’язком системи рівнянь із двома змінними?
3. Що означає розв’язати систему рівнянь?
4. ![]() У чому суть графічного методу розв’язування систем рівнянь із двома змінними?
У чому суть графічного методу розв’язування систем рівнянь із двома змінними?
5. Скільки розв’язків може мати система двох лінійних рівнянь із двома змінними?
6. Яким є взаємне розміщення прямих, що є графіками двох лінійних рівнянь із двома змінними, які складають систему рівнянь, якщо:
1) система має єдиний розв’язок; 2) система не має розв’язків; 3) система має безліч розв’язків?
ВПРАВИ
1119.° Яка з пар чисел (–2; 1), (2; –1), (6; 4), (8; –4) є розв’язком
3x 8y 14,
системи рівнянь
4x y 28?
1120.° Чи є правильним твердження:
y x 5,
1) пара чисел (0; 0) не є розв’язком системи рівнянь
3x 2y 4;
x y 1,
2) пара чисел (–1; 2) є розв’язком системи рівнянь
3x 2y 1;
2y x 4,
3) пара чисел (2; –1) є розв’язком системи рівнянь
2x 3y 1;
x y 8,
4) пара чисел (9; –1) не є розв’язком системи рівнянь
x y 10;
4x 5y 6,
5) система рівнянь не має розв’язків?
5y 4x 7
1121.° Розв’язком яких систем є пара чисел (–5; 2):
7x 2y 31, 3y 2x 16, x 2y 9,
1) 2) 3)
4x 5y 30; 6x 7y 16; 10y x 15?
1122.° Визначте координати точки перетину прямих, зображених на рисунку 70. Запишіть відповідну систему рівнянь, перевірте знайдений розв’язок системи, підставивши координати точки перетину прямих у рівняння системи.
а б
Рис. 70
1123.° Розв’яжіть графічно систему рівнянь:
x y 1, x y 5, 2x y 8,
1) 3) 5) x 2y 7; 4x y 5; 2x y 0;
x y 0, 2x 3y 6, 7x 3y 26,
2) 4) 6) 3x y 4; 3x y 9; y 2x 8.
1124.° Розв’яжіть графічно систему рівнянь:
x 2y 0, 2x 5y 10, x 2y 1, x y 3, 1) 2) 3) 4)
5x y 18; 4x y 2; y x 2; x y 1.
1125.• Складіть яку-небудь систему двох лінійних рівнянь із двома змінними, розв’язком якої є пара значень змінних: 1) x = 3, y = 2; 2) x = –4, y = 1; 3) x = 5, y = 0.
1126.• Складіть яку-небудь систему двох лінійних рівнянь із двома змінними, розв’язком якої є пара чисел (2; –2).
1127.• Пара чисел (6; 4) є розв’язком системи рівнянь: ax 2y 26, 5x by 6,
1) 2)
4x by 14; ax by 0.
Знайдіть значення a і b.
1128.• При яких значеннях a і b пара чисел (–2; 3) є розв’язком
ax 3y 13,
системи рівнянь
7x by 1?
1129.• Чи має розв’язок система рівнянь:
2x 7y 6, 2x y 2, x 2y 0,5,
1) 2) 3)
8x 28y 24; 6x 3y 9; 2x 4y 2?
1130.• Чи має розв’язок система рівнянь:
x y 4, x 1,5y 4, 9x 9y 18,
1) 2) 3)
3x 3y 6; 3y 2x 8; x y 2?
1131.•• До рівняння 2x – 3y = 6 доберіть друге лінійне рівняння таке, щоб отримати систему рівнянь, яка: 1) має єдиний розв’язок; 3) не має розв’язків.
2) має безліч розв’язків;
1132.•• До рівняння x – y = 2 доберіть друге лінійне рівняння таке, щоб отримати систему рівнянь, яка:
1) має єдиний розв’язок; 3) не має розв’язків.
2) має безліч розв’язків;
1133.•• При яких значеннях a не має розв’язків система рівнянь
8x 9y 7,
8x 9y a?
1134.•• При якому значенні a має безліч розв’язків система рівнянь: x 5y 4, 3x ay 12,
1) 2)
4x 20y a; 9x 15y 36?
1135.•• При яких значеннях a система рівнянь:
7x 12y 14,
1) не має розв’язків;
7x 12y a
6x ay 4,
2) має безліч розв’язків?
3x 5y 2
1136.•• Підберіть такі значення a і b, при яких система рівнянь x 2y 3, ax 4y b:
1) має безліч розв’язків; 3) не має розв’язків.
2) має єдиний розв’язок;
1137.•• Підберіть такі значення m і n, при яких система рівнянь x y 5,
3x my n:
1) має безліч розв’язків; 3) не має розв’язків.
2) має єдиний розв’язок;
1138.* Розв’яжіть графічно систему рівнянь:
|x | y 0, |x | y 0, y |x | 0, x |y | 0,
1) 2) 3) 4) x y 4; x 3y 4; x y 2; 2x y 3.
1139.* Розв’яжіть графічно систему рівнянь:
x 2 y 2 0, |y 2x | 3, x 2 2xy y 2 4,
1) 2) 3) x 2y 3; x 2y 0; |x y | 2.
![]()
1140. Математичний гурток відвідують 30 учнів і учениць 5–8 класів. На діаграмі (рис. 71) показано розподіл їх за класами.
![]() Ï’ÿòèêëàñíèêè
Ï’ÿòèêëàñíèêè
Øåñòèêëàñíèêè
Ñåìèêëàñíèêè Âîñüìèêëàñíèêè
Чи є правильним твердження:
1) шестикласників більше, ніж семикласників;
2) восьмикласників більше, ніж разом п’ятикласників і шестикласників;
3) восьмикласників менше, ніж семикласників;
4) семикласники становлять понад 25 % членів гуртка;
5) восьмикласники становлять понад 50 % членів гуртка;
6) шестикласників і семикласників разом 15 осіб;
7) семикласників і восьмикласників разом менше ніж 20 осіб?
1141. Зливок сплаву міді й олова масою 5,5 кг містить міді на 20 % більше, ніж олова. Знайдіть масу міді в цьому зливку.
1142. З Києва до Лубен, відстань між якими дорівнює 200 км, виїхав автобус. Через 32 хв після виїзду автобуса назустріч йому з Лубен виїхав автомобіль зі швидкістю, на 20 км/год більшою за швидкість автобуса. З якою швидкістю рухався автобус, якщо вони зустрілися через 1,2 год після виїзду автомобіля?
1143. Знайдіть чотири послідовних непарних натуральних числа, сума квадратів яких дорівнює 164.
1144. Доведіть, що коли x + y = a – 1, то ax + x + ay + y + 1 = a2.
1145. Остача при діленні числа a на 5 дорівнює 4, а остача при діленні на 5 числа b дорівнює 3. Доведіть, що значення виразу a2 + b2 кратне 5.
![]() ГОТУЄМОСЯ ДО ВИВЧЕННЯ НОВОЇ ТЕМИ
ГОТУЄМОСЯ ДО ВИВЧЕННЯ НОВОЇ ТЕМИ
1146. Виразіть y через x і x через y з рівняння:
1) x + y = 10; 3) y – x = –4; 5) 5y – 4x = 0; 2) 2x + y = 7; 4) x – 6y = 1; 6) 4x + 3y = –12.
 УЧИМОСЯ РОБИТИ НЕСТАНДАРТНІ КРОКИ
УЧИМОСЯ РОБИТИ НЕСТАНДАРТНІ КРОКИ
1147. Десятковий запис одного п’ятицифрового числа складається тільки із цифр 2 і 3, а другого п’ятицифрового числа — тільки із цифр 3 і 4. Чи може запис добутку цих чисел складатися тільки із цифр 2 і 4?
![]() 27. Розв’язування систем лінійних рівнянь
27. Розв’язування систем лінійних рівнянь
методом підстановки
Якщо математикам трапляється нова задача, то зазвичай вони намагаються звести її розв’язування до розв’язування вже знайомої задачі.
Покажемо, як розв’язування системи лінійних рівнянь із двома змінними можна звести до розв’язування лінійного рівняння з однією змінною. А з останньою задачею ви вже знайомі.
27. озв’язування систем лінійних рівнянь методом підстановки
![]()
Розв’яжемо систему рівнянь
2x y 8,
3x 2y 5.
З першого рівняння виразимо змінну y через змінну x:
y 2x 8.
Підставимо в друге рівняння системи замість змінної y вираз
2x – 8. Отримаємо систему
2x y 8,
3x 2 (2x 8) 5.
Ця система та вихідна мають одні й ті самі розв’язки. Приймемо тут цей факт без обґрунтувань. Ви можете розглянути доведення цього факту на заняттях математичного гуртка.
Друге рівняння останньої системи є рівнянням з однією змінною. Розв’яжемо його:
3x 2 (2x 8) 5;
3x 4x 16 5;
7x = 21; x = 3.
Підставимо знайдене значення змінної x у рівняння y = 2x – 8. Отримаємо: y = 2æ3 – 8; y = –2.
Пара чисел (3; –2) — шуканий розв’язок.
Описаний тут спосіб розв’язування системи називають методом підстановки.
Отже, щоб розв’язати систему двох лінійних рівнянь методом підстановки, треба:
1) виразити з будь-якого рівняння системи одну змінну через другу;
2) підставити в інше рівняння системи замість цієї змінної вираз, отриманий на першому кроці;
3) розв’язати рівняння з однією змінною, отримане на другому кроці;
4) підставити знайдене значення змінної у вираз, отриманий на першому кроці;
5) обчислити значення другої змінної; 6) записати відповідь.
Цю послідовність дій можна назвати алгоритмом розв’язування системи двох лінійних рівнянь із двома змінними методом підстановки.
![]()
1148.° Розв’яжіть систему рівнянь:
y 3x 1, 2x y 10, 15 x 2y,
1) 4) 7)
2x y 9; 4x 7y 2; 4x 3y 27;
x 2y 8, 5y x 8, 5x y 6,2,
2) 5) 8)
x 4y 4; 5x 4y 23; 0,8x 3y 13.
x 6y, 3x 4y 0,
3) 6)
x 5y 88; 2x 5y 46;
1149.° Знайдіть розв’язок системи рівнянь:
4x y 12, 4y x 11, x y 7,
1) 3) 5)
7x 2y 20; 5x 2y 17; 9y 2x 25;
x 2y 5, 6x y 1, 5x 3y 0,
2) 4) 6)
3x 8y 1; 2x 3y 11; 15x 2y 55.
1150.• Розв’яжіть систему рівнянь:
4x 3y 15, 4x 5y 1,
1) 4)
3x 4y 6; 8x 2y 38;
2x 3y 2, 5a 4b 3,
2) 5)
5x 2y 24; 2a 3b 11;
5y 6x 4, 8m 2n 11,
3) 6)
7x 4y 1; 9m 4n 8.
1151.• Розв’яжіть систему рівнянь:
5x 2y 15, 8p 5q 11,
1) 3)
8x 3y 20; 5p 4q 6;
7x 4y 5, 6u 5v 38,
2) 4)
3x 2y 3; 2u 7v 22.
1152.• Знайдіть розв’язок системи рівнянь:
6 5 (x y) 7x 4y, 6y 5x 1,
![]() 1) 3 (x 1) (6x 8y) 69 3y; 3) x 1 3y x 4
1) 3 (x 1) (6x 8y) 69 3y; 3) x 1 3y x 4 ![]() ;
;
![]()
x2 3y 2, 4) 3 8 y 3,
2)
5x y 34; ![]() x 0,5.
x 0,5.
27. озв’язування систем лінійних рівнянь методом підстановки
![]()
1153.• Розв’яжіть систему рівнянь:
x y x y
6x 3 5x 4 (5y 4), 8 6 4,
1) 3)
3 (2x 3y) 6x 8 y; 3x y 2x 5y 5.
4 3
x 3 y 4 1,
2) 2 7
6y x 5;
![]()
1154. Під час роботи ліхтарика батарейка розряджається, і напруга в електричному колі ліхтарика зменшується. На рисунку 72 зображено графік зміни напруги в колі під час роботи ліхтарика. Користуючись цим графіком, визначте:
1) якою була напруга в колі: а) в момент включення ліхтарика;
б) через 6 год після початку роботи ліхтарика;
2) через скільки годин після включення ліхтарика напруга дорівнювала 1 В;
3) за скільки годин роботи напруга зменшилася від 1,6 В до 1,2 В.
Рис. 72 1155. Знайдіть значення виразу:
1) m (m – 3) (m + 3) – (m – 2) (m2 + 2m + 4) при m ![]() ;
;
2) (6m – n) (6m + n) – (12m – 5n) (3m + n) при m ![]() , n =
, n = ![]() .
.
1156. (Задача з болгарського фольклору.) Троє чоловіків прийшли до перукаря. Той поголив першого й сказав: «Подивись, скільки грошей у шухляді стола, поклади ще стільки ж і візьми 8 левів[13] решти». Те саме перукар сказав і другому, і третьому. Після того як усі троє пішли, виявилося, що в касі немає грошей. Скільки грошей було в касі перед тим, як заплатив перший чоловік?
1157. Функцію задано формулою y = 6 – kx. При якому значенні k графік функції проходить через точку A (4; –2)?
1158. Доведіть, що значення виразу 24n – 1 ділиться націло на 5 при будь-якому натуральному значенні n.
1159. Знайдіть три останні цифри значення виразу 23763 + 16243.
1160. Остачі при діленні на 6 чисел a і b дорівнюють 2 і 3 відповідно. Доведіть, що значення добутку ab кратне 6.
 УЧИМОСЯ РОБИТИ НЕСТАНДАРТНІ КРОКИ
УЧИМОСЯ РОБИТИ НЕСТАНДАРТНІ КРОКИ
1161. Знайдіть усі цілі числа x і y, при яких виконується рівність x + y = xy.
![]() 28. Розв’язування систем лінійних рівнянь
28. Розв’язування систем лінійних рівнянь
методом додавання
Розглянемо ще один спосіб, який дає змогу звести розв’язування системи двох лінійних рівнянь із двома змінними до розв’язування лінійного рівняння з однією змінною.
Розв’яжемо систему рівнянь
2x 5y 7, 4x 5y 5.
Оскільки в цій системі коефіцієнти при змінній y є протилежними числами, то рівняння з однією змінною можна отримати, додавши почленно ліві й праві частини рівнянь системи. Запишемо: 2x – 5y + 4x + 5y = 7 + 5; 6x = 12.
x = 2.
Підставити знайдене значення змінної x можна в будь-яке з рівнянь системи. Підставимо, наприклад, у перше. Отримаємо:
2æ2 – 5y = 7;
–5y = 3; y = –0,6.
Отже, розв’язком системи є пара чисел (2; –0,6).
Описаний спосіб розв’язування системи називають методом додавання.
Цей метод заснований на такому твердженні: якщо одне з рівнянь системи замінити на рівняння, отримане шляхом додавання лівих і правих частин рівнянь системи, то отримана система буде мати такі самі розв’язки, що й початкова (приймемо цей факт без доведення).
2x 5y 7,
Так, розв’язуючи систему ми замінили її на систе-
4x 5y 5,
2x 5y 4x 5y 7 5, му
2x 5y 7.
Розв’яжемо ще одну систему:
2x 3y 11,
6x 5y 19.
Якщо додати почленно ліві й праві частини рівнянь системи, то знову отримаємо рівняння з двома змінними. Дана система ще «не готова» до застосування методу додавання.
Помножимо обидві частини першого рівняння на –3. Отримає-
6x 9y 33,
мо систему розв’язки якої збігаються з розв’язками 6x 5y 19,
вихідної системи.
Для такої системи метод додавання вже буде ефективним. Маємо:
–6x + 9y + 6x + 5y = –33 + 19;
14y = –14; y = –1.
Підставимо знайдене значення y в перше рівняння вихідної системи. Отримаємо:
2x – 3æ(–1) = 11;
2x = 8; x = 4.
Пара чисел (4; –1) — шуканий розв’язок.
Розглянемо систему, у якій одразу два рівняння треба підготувати до застосування методу додавання:
7x 8y 9, 3x 5y 7.
Щоб виключити змінну y, помножимо обидві частини першого рівняння на число 5, а другого — на число –8 і застосуємо метод додавання:
35x 40y 45,
24x 40y 56;
35x + 40y – 24x – 40y = 45 – 56;
11x = –11; x = –1.
Підставивши знайдене значення x у перше рівняння даної системи, отримаємо:
–7 + 8y = 9; y = 2.
Отже, пара чисел (–1; 2) — розв’язок даної системи.
Щоб розв’язати систему двох лінійних рівнянь методом додавання, треба:
1) дібравши «вигідні» множники, перетворити одне чи обидва рівняння системи так, щоб коефіцієнти при одній зі змінних стали протилежними числами;
2) додати почленно ліві й праві частини рівнянь, отриманих на першому кроці;
3) розв’язати рівняння з однією змінною, отримане на другому кроці;
4) підставити знайдене на третьому кроці значення змінної в будь-яке з рівнянь вихідної системи; 5) обчислити значення другої змінної; 6) записати відповідь.
![]()
1162.° Запишіть рівняння, яке отримаємо, додавши почленно ліві й праві частини рівнянь системи:
2x y 6, 4x 7y 8,
1) 2)
3x y 4; 6y 4x 1.
1163.° На яке число треба помножити обидві частини першого рівняння системи, щоб у рівняннях коефіцієнти при змінній y стали протилежними числами:
4x y 7, 2x 4y 9,
1) 2)
5x 6y 30; 3x 20y 40?
1164.° На яке число треба помножити обидві частини першого рівняння системи, щоб у рівняннях коефіцієнти при змінній x стали протилежними числами:
3x 7y 21, 7x 3y 8,
1) 2)
3x 9y 2; 28x 5y 12?
1165.° На яке число треба помножити обидві частини першого рівняння системи, а на яке — обидві частини другого рівняння, щоб у рівняннях коефіцієнти при змінній y стали протилежними числами:
2x 6y 7, 7x 6y 22,
1) 2)
5x 4y 3; 35x 9y 34?
1166.° Розв’яжіть систему рівнянь методом додавання:
x y 6, 2x 9y 11, 8x y 8,
1) 3) 5)
x y 8; 7x 9y 25; 12x y 4;
3x y 14, 6x y 16, 7x 5y 29,
2) 4) 6)
5x y 10; 6x 4y 34; 7x 8y 10.
1167.° Розв’яжіть систему рівнянь методом додавання:
4x y 20, 5x 7y 2,
1) 3)
4x y 12; 8x 7y 15;
9x 17y 52, 9x 6y 24,
2) 4)
26x 17y 18; 9x 8y 10.
1168.• Розв’яжіть систему рівнянь методом додавання: x 3y 5, 3x 4y 16,
1) 5)
4x 9y 41; 5x 6y 14;
10x 2y 12, 2x 3y 6,
2) 6)
5x 4y 6; 3x 5y 8;
3x 2y 1, 5u 7v 24,
3) 7)
12x 7y 26; 7u 6v 2;
3x 8y 13, 0,2x 1,5y 10,
4) 8)
2x 3y 17; 0,4x 0,3y 0,2.
1169.• Розв’яжіть систему рівнянь методом додавання:
5x y 7, 5x 2y 16, 4a 6b 9,
1) 3) 5)
7x 4y 1; 8x 3y 38; 3a 5b 2;
6x 5y 23, 5x 4y 10, 9m 13n 22,
2) 4) 6)
2x 7y 13; 2x 3y 3; 2m 3n 1.
1170.• Розв’яжіть систему рівнянь:
2 (4x 5) 3 (3 4y) 5, x2 3y 3,
1) 3)
7 (6y 1) (4 3x) 21y 86; 3x 5y 4;
4 6
2 (2x 1) 2,5 3 (y 2) 8x , x 6 2 y153 1,
2) 4)
8 5 (4 x) 6y (5 x); x 2,5 y 3 1.
9 6 3
1171.• Розв’яжіть систему рівнянь:
15x 3y 3x 2y
0,2x 0,3 (2y 1) 1,5, 4 6 3,
1) 2)
3 (x 1) 3y 2y 2; 3x y x 3y 6.
3 2
1172.• Знайдіть розв’язок системи рівнянь:
(x 3)2 4y (x 2) (x 1) 6,
1)
(x 4) (y 6) (x 3) (y 7) 3;
(x y) (x y) x (x 10) y (5 y) 15, 2) (x 1)2 (y 1)2 (x 4)2 (y 2)2 18.
1173.• Розв’яжіть систему рівнянь:
(2x 1)2 (2x y) (2x y) (y 8) (y 10),
1)
4x (x 5) (2x 3) (2x 9) 6y 104;
(x 2) (x 2 2x 4) x (x 4) (x 4) 20 20y,
2)
(3x 2) (4y 5) 2y (6x 1) 58.
1174.• Знайдіть, не виконуючи побудови, координати точки перетину прямих:
1) y = 2 – 3x і 2x + 3y = 7; 2) 5x + 6y = –20 і 2x + 9y = 25.
1175.• Знайдіть, не виконуючи побудови, координати точки перетину прямих:
1) 2x – 3y = 8 і 7x – 5y = –5; 2) 9x + y = 3 і 8x + 3y = –10.
1176.• При яких значеннях a і b графік рівняння ax + by = 8 проходить через точки A (1; 3) і B (2; –4)?
1177.• При яких значеннях m і n графік рівняння mx – ny = 6 проходить через точки C (2; –1) і D (–6; 5)?
1178.• Запишіть рівняння прямої y = kx + b, яка проходить через точки:
1) M (2; 1) і K (–3; 2); 2) P (–4; 5) і Q (4; –3).
1179.• Запишіть рівняння прямої y = kx + b, яка проходить через точки:
1) A (3; 2) і B (–1; 4); 2) C (–2; –3) і D (1; 6).
1180.• Чи має розв’язок система рівнянь:
2x y 5, 2x 3y 1,
1) 3x 4y 24, 2) 3x 5y 1, x 2y 9; 5x 9y 5?
1181.• Розв’яжіть систему рівнянь:
6x 5y 10, x 2y 1,
1) 8x 5y 32, 2) 2x y 7,
3x 10y 7; 4x y 14.
1182.• Запишіть систему лінійних рівнянь із двома змінними, графіки яких зображено на рисунку 73.
б г
Рис. 73
а б
Рис. 74
1183.• Запишіть систему лінійних рівнянь із двома змінними, графіки яких зображено на рисунку 74.
1184.•• При якому значенні k пряма y = kx + 2 проходить через точку перетину прямих 3x + 5y = 5 і 7x – 4y = 43?
1185.•• При якому значенні a має розв’язок система рівнянь
8x 7y 21, 5x 3y 20, ax 2y 24?
1186.•• Розв’яжіть рівняння:
1) (x + y)2 + (x – 3)2 = 0;
2) (x + 2y – 3)2 + x2 – 4xy + 4y2 = 0;
3) | x – 3y – 6 | + (9x + 6y – 32)2 = 0;
4) x2 + y2 + 10x – 12y + 61 = 0; 5) 25x2 + 10y2 – 30xy + 8y + 16 = 0. 1187.•• Розв’яжіть рівняння:
1) (x – 2y)2 + (y – 5)2 = 0;
2) (4x + 2y – 5)2 + | 4x – 6y + 7 | = 0; 3) 50x2 + 4y2 – 28xy + 16x + 64 = 0.
1188.* Розв’яжіть систему рівнянь:
![]() 2 5 15, 5 10 3, x y
2 5 15, 5 10 3, x y
1) 2)
3 8 23;1. x y 3x 2y 2x 3y
1189.* Розв’яжіть систему рівнянь:
![]() 1 7 6, 9 6 2, x y
1 7 6, 9 6 2, x y
1) 2)
2 3 46;1.
x y x 4y 5x y
![]()
1190. Після того як вода в чайнику закипіла, його вимкнули. На рисунку 75 зображено графік зміни температури води в чайнику. Користуючись графіком, визначте:
1) якою була температура води через 10 хв після вимкнення чайника;
2) через скільки хвилин після вимкнення температура води становила 30 °С;
3) за скільки хвилин температура води знизилася від 60 °С до 40 °С.
Рис. 75
1191. Оптова ціна коробки цукерок — 130 грн. Роздрібна ціна в магазині на 30 % вища за оптову. Яку найбільшу кількість таких коробок можна купити в магазині, маючи 2500 грн?
1192. Знайдіть значення виразу:
1) (a2 + 1)2 + (a – 1) (a2 + 1) – a2, якщо a = –2;
2) (a – 1) (a2 + 1) (a + 1) – (a2 + 1)2, якщо a = ![]() .
.
1193. На математичній олімпіаді учасникам було запропоновано розв’язати 12 задач. За кожну правильно розв’язану задачу нараховували 5 балів, а за нерозв’язану — знімали 3 бали. Скільки задач розв’язав правильно учень, який отримав у підсумку 36 балів?
1194. (Задача з німецького фольклору.) За який час лев, вовк і собака можуть з’їсти трьох овець, якщо лев один може з’їсти вівцю за 1 год, вовк — за 3 год, а собака — за 6 год?
1195. Доведіть, що різниця квадратів двох довільних натуральних чисел, кожне з яких не ділиться націло на 3, є кратною 3.
1196. У саду дерев більше за 90, але менше від 100. Третина всіх дерев — яблуні, а чверть усіх дерев — сливи. Скільки дерев у саду?
1197. Який із виразів набуває тільки від’ємних значень при будьякому значенні x:
1) –x2 – 4x + 6; 2) –x2 + 16x – 64; 3) –x2 + 8x – 18?
 УЧИМОСЯ РОБИТИ НЕСТАНДАРТНІ КРОКИ
УЧИМОСЯ РОБИТИ НЕСТАНДАРТНІ КРОКИ
1198. Клітинки таблиці розміром 101 × 101 заповнено числами так, що добуток чисел у кожному стовпці є від’ємним. Чи може виявитися, що кількість рядків, добуток чисел у яких додатний, дорівнює 51?
![]() 29. Розв’язування задач за допомогою систем лінійних рівнянь
29. Розв’язування задач за допомогою систем лінійних рівнянь
Розглянемо задачі, у яких системи двох лінійних рівнянь із двома змінними використовують як математичні моделі реальних ситуацій.
![]() ПРИКЛАД 1 На пошиття одного плаття та чотирьох спідниць витратили 9 м тканини, а на пошиття трьох таких самих платтів та восьми таких самих спідниць — 21 м тканини. Скільки метрів тканини треба для пошиття одного плаття та однієї спідниці окремо?
ПРИКЛАД 1 На пошиття одного плаття та чотирьох спідниць витратили 9 м тканини, а на пошиття трьох таких самих платтів та восьми таких самих спідниць — 21 м тканини. Скільки метрів тканини треба для пошиття одного плаття та однієї спідниці окремо?
Розв’язання. Нехай на одне плаття витрачають x м тканини, а на одну спідницю — y м. Тоді на одне плаття та 4 спідниці треба (x + 4y) м тканини, що за умовою становить 9 м. Отже, x + 4y = 9.
На 3 плаття та 8 спідниць потрібно (3x + 8y) м тканини, або 21 м. Отже, 3x + 8y = 21. Маємо систему рівнянь
x 4y 9,
3x 8y 21.
Розв’язавши цю систему, отримуємо: x = 3, y = 1,5. Отже, на пошиття одного плаття треба 3 м тканини, а однієї спідниці — 1,5 м.
![]() Відповідь: 3 м, 1,5 м.
Відповідь: 3 м, 1,5 м. ¤
![]() ПРИКЛАД 2 З міста A до міста B, відстань між якими 264 км, виїхав мотоцикліст. Через 2 год після цього назустріч йому з міста B виїхав велосипедист, який зустрівся з мотоциклістом через 1 год після свого виїзду. Знайдіть швидкість кожного з них, якщо за 2 год мотоцикліст проїжджає на 40 км більше, ніж велосипедист за 5 год.
ПРИКЛАД 2 З міста A до міста B, відстань між якими 264 км, виїхав мотоцикліст. Через 2 год після цього назустріч йому з міста B виїхав велосипедист, який зустрівся з мотоциклістом через 1 год після свого виїзду. Знайдіть швидкість кожного з них, якщо за 2 год мотоцикліст проїжджає на 40 км більше, ніж велосипедист за 5 год.
Розв’язання. Нехай швидкість мотоцикліста дорівнює x км/год, а велосипедиста — y км/год. До зустрічі мотоцикліст рухався 3 год і проїхав 3x км, а велосипедист відповідно — 1 год та y км. Разом вони проїхали 264 км. Тоді 3x + y = 264.
Велосипедист за 5 год проїжджає 5y км, а мотоцикліст за 2 год — 2x км, що на 40 км більше за 5y км. Тоді 2x – 5y = 40.
Отримали систему рівнянь
3x y 264,
2x 5y 40,
розв’язком якої є пара чисел x = 80, y = 24.
Отже, швидкість мотоцикліста дорівнює 80 км/год, а велосипедиста — 24 км/год.
![]() Відповідь: 80 км/год, 24 км/год.
Відповідь: 80 км/год, 24 км/год. ¤
![]() ПРИКЛАД 3 Стіл і стілець коштували разом 680 грн. Після того як стіл подешевшав на 20 %, а стілець подорожчав на 10 %, вони стали коштувати разом 580 грн. Знайдіть початкову ціну стола та початкову ціну стільця.
ПРИКЛАД 3 Стіл і стілець коштували разом 680 грн. Після того як стіл подешевшав на 20 %, а стілець подорожчав на 10 %, вони стали коштувати разом 580 грн. Знайдіть початкову ціну стола та початкову ціну стільця.
Розв’язання. Нехай початкова ціна стола становила x грн, а стільця — y грн. Тоді за умовою x + y = 680.
Нова ціна стола становить 80 % початкової та дорівнює 0,8x грн. Нова ціна стільця становить 110 % початкової та дорівнює 1,1y грн.
Тоді 0,8x + 1,1y = 580. Отримали систему рівнянь
x y 680,
0,8x 1,1y 580.
Розв’язком цієї системи є пара x = 560, y = 120.
![]() Отже, початкова ціна стола була 560 грн, а стільця — 120 грн. Відповідь: 560 грн, 120 грн.
Отже, початкова ціна стола була 560 грн, а стільця — 120 грн. Відповідь: 560 грн, 120 грн. ¤
![]() ПРИКЛАД 4 Скільки грамів 3 %-го та скільки грамів 8 %-го розчинів солі треба взяти, щоб отримати 500 г 4 %-го розчину?
ПРИКЛАД 4 Скільки грамів 3 %-го та скільки грамів 8 %-го розчинів солі треба взяти, щоб отримати 500 г 4 %-го розчину?
Розв’язання. Нехай першого розчину треба взяти x г, а другого — y г. Тоді за умовою x + y = 500.
У 3 %-му розчині міститься 0,03x г солі, а у 8 %-му — 0,08y г солі. У 500 г 4 %-го розчину міститься 500æ0,04 = 20 (г) солі. Отже, 0,03x + 0,08y = 20.
Складаємо систему рівнянь
x y 500,
0,03x 0,08y 20, x 400,
розв’язавши яку матимемо:
y 100.
![]() Отже, треба взяти 400 г 3 %-го розчину та 100 г 8 %-го розчину. Відповідь: 400 г, 100 г.
Отже, треба взяти 400 г 3 %-го розчину та 100 г 8 %-го розчину. Відповідь: 400 г, 100 г. ¤
![]() ПРИКЛАД 5 У Петра були купюри по 5 грн і по 20 грн. Він каже, що купив футбольний м’яч за 255 грн, віддавши за нього 20 купюр, а Ніна стверджує, що такого бути не може. Хто з них має рацію?
ПРИКЛАД 5 У Петра були купюри по 5 грн і по 20 грн. Він каже, що купив футбольний м’яч за 255 грн, віддавши за нього 20 купюр, а Ніна стверджує, що такого бути не може. Хто з них має рацію?
Розв’язання. Нехай було x купюр по 5 грн та y купюр по
20 грн. Тоді
x y 20,
5x 20y 255.
Розв’язком цієї системи є пара 9![]() ;10
;10 ![]() . Проте цей розв’язок не відповідає змісту задачі, оскільки кількість купюр може бути тільки натуральним числом.
. Проте цей розв’язок не відповідає змісту задачі, оскільки кількість купюр може бути тільки натуральним числом.
 Відповідь: має рацію Ніна.
Відповідь: має рацію Ніна.
1199.° Знайдіть два числа, якщо їхня сума дорівнює 63, а різниця дорівнює 19.
1200.° Знайдіть два числа, якщо їхня різниця дорівнює 23, а сума подвоєного більшого із цих чисел і другого числа дорівнює 22.
1201.° (Задача з оповідання «Репетитор» А. П. Чехова[14].) Купець купив 138 аршинів[15] чорного та синього сукна за 540 рублів. Запитання: скільки аршинів він купив того й другого, якщо синє коштувало 5 рублів за аршин, а чорне — 3 рублі?
1202.° Група із 46 туристів і туристок вирушила в похід на 10 човнах, частина з яких були чотиримісними, а решта — шестимісними. Скільки було човнів кожного виду?
1203.° Щоб нагодувати 4 коней і 12 корів, потрібно 120 кг сіна на день, а щоб нагодувати 3 коней і 20 корів — 167 кг сіна. Знайдіть денну норму сіна для коня та для корови.
1204.° За перший день 2 гусеничних трактори й один колісний зорали 22 га, а за другий день 3 гусеничних і 8 колісних — 72 га. Знайдіть, скільки гектарів землі може зорювати щодня один гусеничний трактор і скільки — один колісний.
1205.° Двоє робітників виготовили 135 деталей. Перший робітник працював 7 днів, а другий — 12 днів. Скільки деталей виготовляв щодня кожний робітник, якщо перший за 3 дні зробив на 3 деталі більше, ніж другий — за 4 дні?
1206.° Дві бригади працювали на збиранні яблук. Першого дня одна бригада працювала 5 год, а друга — 4 год, причому разом вони зібрали 40 ц яблук. Наступного дня бригади працювали з тією самою продуктивністю праці, при цьому перша бригада зібрала за 3 год на 2 ц більше, ніж друга — за 2 год. Скільки центнерів яблук збирала кожна бригада за 1 год?
1207.° За 6 наборів олівців і 5 циркулів заплатили 144 грн. Скільки коштує набір олівців і скільки — циркуль, якщо 3 набори олівців дорожчі за один циркуль на 30 грн?
1208.° За 11 зошитів і 8 ручок заплатили 49 грн. Скільки коштує 1 зошит і скільки — 1 ручка, якщо 5 зошитів дорожчі за 4 ручки на 7 грн?
1209.° Із Києва й Вінниці, відстань між якими 256 км, виїхали одночасно назустріч один одному автобус і автомобіль, які зустрілися через 2 год після початку руху. Знайдіть швидкість кожного з них, якщо автобус за 2 год проїжджає на 46 км більше, ніж автомобіль за 1 год.
1210.° Із двох станцій, відстань між якими 300 км, одночасно назустріч один одному вирушили пасажирський і товарний поїзди, які зустрілися через 3 год після початку руху. Якби пасажирський поїзд вирушив на 1 год раніше від товарного, то вони зустрілися б через 2,4 год після виходу товарного поїзда. Знайдіть швидкість кожного поїзда.
1211.• Із села до станції вийшов пішохід. Через 30 хв із цього села до станції виїхав велосипедист, який наздогнав пішохода через 10 хв після виїзду. Знайдіть швидкість кожного з них, якщо за 3 год пішохід проходить на 4 км більше, ніж велосипедист проїжджає за півгодини.
1212.• Із Житомира до Одеси, відстань між якими 536 км, виїхав перший автомобіль. Через 2,5 год після початку руху першого автомобіля назустріч йому з Одеси виїхав другий автомобіль, який зустрівся з першим через 2 год після свого виїзду. Знай діть швидкість кожного автомобіля, якщо перший за 2 год проїжджає на 69 км менше, ніж другий за 3 год.
1213.• У двох бідонах було молоко. Якщо з першого бідона перелити в другий 10 л молока, то в обох бідонах молока стане порівну. Якщо з другого бідона перелити в перший 20 л молока, то в першому стане у 2,5 раза більше молока, ніж у другому.
Скільки літрів молока було в кожному бідоні?
1214.• Коли до першого вагона електропотяга ввійшли 4 пасажири, а з другого вагона вийшли 4 пасажири, то в обох вагонах пасажирів стало порівну. Якби до першого вагона ввійшли 2 пасажири, а до другого — 24 пасажири, то в першому вагоні стало б у 2 рази менше пасажирів, ніж у другому. Скільки пасажирів було спочатку в кожному вагоні?
1215.• Моторний човен за 3 год руху проти течії річки та 2,5 год за течією проходить 98 км. Знайдіть власну швидкість човна та швидкість течії, якщо за 5 год руху за течією він проходить на 36 км більше, ніж за 4 год проти течії річки.
1216.• Катер за 5 год руху за течією річки проходить на 70 км більше, ніж за 3 год руху проти течії. Знайдіть швидкість катера в стоячій воді та швидкість течії, якщо за 9 год руху озером він проходить стільки ж кілометрів, скільки за 10 год руху проти течії річки.
1217.• (Задача з грецького фольклору.) Віслюк і мул ідуть поруч з вантажем на спині. Віслюк скаржиться на непосильну ношу, а мул відповідає: «Чого ти скаржишся? Адже якщо я візьму один твій мішок, то моя ноша стане вдвоє важча за твою. А якщо ти візьмеш один мій мішок, то твоя поклажа зрівняється з моєю». Скажіть же, мудрі математики, скільки мішків ніс віслюк і скільки ніс мул?
1218.• (Задача з індійського фольклору.) Один каже другому: «Дай мені 100 рупій, і я буду вдвоє багатший за тебе». Другий відповідає: «А якщо ти даси мені 10 рупій, то я стану в 6 разів багатший за тебе». Скільки грошей було в кожного?
1219.• Син 6 років тому був у 4 рази молодший від батька, а через 12 років він буде молодшим від батька у 2 рази. Скільки років батькові та скільки — синові?
1220.• Бабуся 6 років тому була в 9 разів старша за онуку, а 4 роки тому — у 7 разів старша. Скільки років бабусі та скільки —
онуці?
1221.• Дві майстерні мали пошити 75 костюмів. Коли перша майстерня виконала 60 % замовлення, а друга — 50 %, то виявилося, що перша майстерня пошила на 12 костюмів більше, ніж друга. Скільки костюмів мала пошити кожна майстерня?
1222.• Михайло та Галина мали разом 60 грн. Коли Михайло витратив ![]() своїх грошей на придбання довідника з математики, а Галина —
своїх грошей на придбання довідника з математики, а Галина — ![]() своїх грошей на придбання довідника з української мови, то виявилося, що Михайло витратив на 1 грн менше, ніж Галина. Скільки грошей було в кожного з них спочатку?
своїх грошей на придбання довідника з української мови, то виявилося, що Михайло витратив на 1 грн менше, ніж Галина. Скільки грошей було в кожного з них спочатку?
1223.• Відомо, що 4 кг огірків і 3 кг помідорів коштували 24 грн. Після того як огірки подорожчали на 50 %, а помідори подешевшали на 20 %, за 2 кг огірків і 5 кг помідорів заплатили 25 грн. Знайдіть початкову ціну 1 кг огірків і 1 кг помідорів.
1224.• Відомо, що 2 банки фарби та 3 банки оліфи коштували 64 грн. Після того як фарба подешевшала на 50 %, а оліфа подорожчала на 40 %, за 6 банок фарби та 5 банок оліфи заплатили 116 грн. Знайдіть початкову ціну однієї банки фарби та однієї банки оліфи.
1225.• Вкладник поклав у банк 1400 грн на два різних рахунки. За першим із них банк виплачує 4 % річних, а за другим — 6 % річних. Через рік вкладник одержав 68 грн відсоткових грошей. Скільки гривень він поклав на кожний рахунок?
1226.• Вкладниця поклала в банк 1200 грн на два різних рахунки. За першим із них банк виплачує 5 % річних, а за другим — 7 % річних. Через рік вкладниця отримала за 5 %-м вкладом на 24 грн відсоткових грошей більше, ніж за другим. Скільки гривень вона поклала на кожний рахунок?
1227.• Відомо, що 60 % числа a на 2 більші за 70 % числа b, а 50 % числа b на 10 більші за ![]() числа a. Знайдіть числа a і b.
числа a. Знайдіть числа a і b.
1228.• Відомо, що 25 % одного числа дорівнюють 20 % другого числа, а ![]() першого числа на 4 менша від 40 % другого. Знайдіть дані числа.
першого числа на 4 менша від 40 % другого. Знайдіть дані числа.
1229.• Маємо два сплави міді й цинку. Перший сплав містить 9 %, а другий — 30 % цинку. Скільки кілограмів кожного сплаву треба взяти, щоб одержати 300 кг сплаву, який містить 23 % цинку?
1230.• Маємо два водно-сольових розчини. Перший розчин містить 25 %, а другий — 40 % солі. Скільки кілограмів кожного розчину треба взяти, щоб одержати 50 кг розчину, який містить 34 % солі?
1231.• Сума цифр двоцифрового числа дорівнює 15. Якщо поміняти його цифри місцями, то отримаємо число, яке менше від даного на 9. Знайдіть дане число.
1232.• Периметр прямокутника дорівнює 28 см. Якщо дві протилежні його сторони збільшити на 6 см, а дві інші зменшити на 2 см, то його площа збільшиться на 24 см2. Знайдіть сторони даного прямокутника.
1233.• Якщо кожну сторону прямокутника збільшити на 3 см, то його площа збільшиться на 45 см2. Якщо дві протилежні сторони збільшити на 4 см, а дві інші зменшити на 5 см, то його площа зменшиться на 17 см2. Знайдіть сторони даного прямокутника.
1234.• Із двох селищ, відстань між якими дорівнює 45 км, одночасно назустріч одне одному вирушили велосипедистка й пішохід, які зустрілися через 3 год після початку руху. Якби велосипедистка виїхала на 1 год 15 хв раніше, ніж вийшов пішохід, то вони зустрілися б через 2 год після виходу пішохода. З якими швидкостями рухалися велосипедистка й пішохід?
1235.• З пунктів A і B, відстань між якими дорівнює 24 км, одночасно назустріч одна одній вирушили дві туристки. Через 2 год після початку руху вони ще не зустрілися, а відстань між ними становила 6 км. Ще через 2 год одній з них залишилося пройти до пункту B на 4 км менше, ніж другій — до пункту A. Знайдіть швидкість кожної туристки.
1236.•• Велосипедист проїхав з пункту A до пункту B за запланований час, рухаючись із певною швидкістю. Якби він збільшив швидкість на 3 км/год, то прибув би до пункту B на 1 год раніше, а якби він проїжджав за годину на 2 км менше, то прибув би на 1 год пізніше. Знайдіть швидкість велосипедиста.
1237.•• Вантаж було перевезено певною кількістю машин з однаковою вантажопідйомністю. Якби на кожній машині вантажу було на 1 т більше, то вантажівок треба було б на 3 менше, а якби вантажу було на 2 т більше, то вантажівок треба було б на 5 мен- ше. Знайдіть масу вантажу, який перевезли.
1238.•• Відстань між двома станціями пасажирський поїзд проходить на 3 год швидше за товарний, а поїзд-експрес — на 1 год швидше за пасажирський. Швидкість товарного поїзда на 25 км/год менша від швидкості пасажирського, а швидкість експреса на 15 км/год більша за швидкість пасажирського. Знайдіть швидкість кожного поїзда та відстань між станціями.
1239.•• Автобус і маршрутне таксі виїжджають щодня назустріч одне одному за розкладом о 8 год з міст Вишневе та Яблуневе й зустрічаються о 8 год 10 хв. Відстань між містами — 18 км.
Одного дня автобус виїхав за розкладом, а таксі — із запізненням — о 8 год 9 хв. Тому зустрілися вони того дня о 8 год 15 хв. Знай діть швидкості автобуса та маршрутного таксі.
1240.•• З міста Сонячне до села Веселе о 9 год 5 хв і 9 год 45 хв виїхали з однаковою швидкістю два автобуси. З Веселого до Сонячного о 9 год 30 хв виїхав велосипедист, який зустрівся з першим автобусом о 9 год 45 хв, а з другим — о 10 год 15 хв. Знайдіть швидкості автобусів і велосипедиста, якщо відстань між Сонячним і Веселим становить 36 км.
1241.•• Маса суміші, яка складається з двох речовин, становила 800 г. Після того як з неї виділили ![]() маси однієї речовини та 60 % маси другої, першої речовини в ній залишилося на 72 г менше, ніж другої. Скільки грамів кожної речовини було в суміші спочатку?
маси однієї речовини та 60 % маси другої, першої речовини в ній залишилося на 72 г менше, ніж другої. Скільки грамів кожної речовини було в суміші спочатку?
1242.•• У зливку сплаву міді та цинку останнього було на 48 кг менше, ніж міді. Після того як зі сплаву виділили ![]() маси міді, що містилася в ньому, і 80 % маси цинку, маса зливку сплаву стала дорівнювати 10 кг. Скільки кілограмів кожної речовини було у зливку сплаву спочатку?
маси міді, що містилася в ньому, і 80 % маси цинку, маса зливку сплаву стала дорівнювати 10 кг. Скільки кілограмів кожної речовини було у зливку сплаву спочатку?
1243.•• Сума цифр двоцифрового числа дорівнює 9, причому цифра в розряді десятків більша за цифру в розряді одиниць. При діленні даного числа на різницю його цифр отримують неповну частку 14 і остачу 2. Знайдіть дане число.
1244.•• Різниця цифр двоцифрового числа дорівнює 6, причому цифра в розряді десятків менша від цифри в розряді одиниць. Якщо ж поділити дане число на суму його цифр, то отримаємо неповну частку 3 й остачу 3. Знайдіть дане число.
1245.* В одному баку було 12 л води, а в другому — 32 л. Якщо перший бак долити доверху водою з другого бака, то другий бак залишиться наповненим на половину свого об’єму. Якщо другий бак долити доверху водою з першого, то перший бак залишиться наповненим на шосту частину свого об’єму. Знайдіть об’єм кожного бака.
1246.* У двох посудинах місткістю 40 л і 60 л була деяка кількість води. Якщо в меншу посудину долити доверху води з більшої, то в більшій залишиться ![]() тієї кількості води, що була в ній спочатку. Якщо ж у більшу посудину долити доверху води з меншої, то в меншій залишиться
тієї кількості води, що була в ній спочатку. Якщо ж у більшу посудину долити доверху води з меншої, то в меншій залишиться ![]() тієї кількості води, що була в ній спочатку. Скільки літрів води було в кожній посудині спочатку?
тієї кількості води, що була в ній спочатку. Скільки літрів води було в кожній посудині спочатку?
1247.* Чи існує двоцифрове число, яке задовольняє такі умови: цифра в розряді десятків цього числа на 2 більша за цифру в розряді його одиниць, а різниця між цим числом і числом, записаним тими самими цифрами, але у зворотному порядку, дорівнює: 1) 20; 2) 18? Якщо таке число існує, знайдіть його.
1248.* (Задача Л. М. Толстого[16].) Вийшла в поле артіль косарів. Вона мала викосити дві сіножаті, з яких одна вдвоє більша за другу. Зранку вся артіль косила більшу сіножать, а після полудня артіль розділилася навпіл, і одна половина закінчувала косити більшу сіножать, а друга почала косити меншу. До вечора більшу сіножать було викошено, а від малої залишила ся ділянка. Її викосив другого дня один косар, який працював цілий день. Скільки косарів було в артілі?
![]()
1249. У рівності 4 (0,5x – 3) = 3x + * замініть зірочку таким виразом, щоб утворилося рівняння, яке:
1) не має коренів;
2) має безліч коренів;3) має один корінь.
1250. На рисунку 76 зображено графік руху туристки від заліз-ничної станції до туристичного табору. Користуючись графіком, визначте:
1) скільки кілометрів становить відстань від станції до табору та за скільки годин туристка подолала цю відстань;
2) на якій відстані від станції була туристка через 4 год після початку руху;
3) через скільки годин після виходу зі станції туристка зробила першу зупинку та скільки вона тривала;
4) з якою швидкістю туристка рухалася від станції до першої зупинки;
5) з якою швидкістю туристка рухалася від першої зупинки до другої.
1251. Побудуйте графік функції:
1) y = (2x – 1) (4x2 + 2x + 1) – 8x3;
2) y = (x + 1) (x + 4) – (x + 3)2;
3) y = (0,5x + 2)2 – (0,5x – 1) (0,5x + 1).
Рис. 76
2x 7, якщо x 2,
1252. Побудуйте графік функції y = 1 5, x,якщо 2 m mx 2, x 5, якщо x 2.
Використовуючи побудований графік, визначте, при яких значеннях a пряма y = a має із цим графіком рівно дві спільні точки.
1253. Подайте вираз 12ab у вигляді різниці квадратів двох многочленів. Скільки розв’язків має задача?
1254. Доведіть, що при будь-якому цілому значенні a значення виразу (a – 3) (a2 – a + 2) – a (a – 2)2 + 2a ділиться націло на 3.
1255. Доведіть тотожність (a – bc)2 – 2 (b2c2 – a2) + (bc + a)2 = 4a2.
1256. Розкладіть на множники вираз:
1) 4kn + 6ak + 6an + 9a2; 3) y4 (x2 + 8x + 16) – a8; 2) b6 – 4b4 + 12b2 – 9; 4) 9x2 – 6x – 35.
1257. Відомо, що x + y = a, xy = b, x2 + y2 = c. Знайдіть залежність між a, b і c.
1258. Точки A (2; 3) і B (5; a) належать прямій y = kx. Знайдіть значення a.
1259. Знайдіть такі значення x, при яких вираз (a – 1)2 + 4 (a – 1) – x можна було б розкласти на множники за формулою квадрата суми.
1260. Графіки функцій y = ax + 12 і y = (3 – a) x + a перетинаються в точці з абсцисою 2. Знайдіть ординату точки їхнього перетину.
 УЧИМОСЯ РОБИТИ НЕСТАНДАРТНІ КРОКИ
УЧИМОСЯ РОБИТИ НЕСТАНДАРТНІ КРОКИ
1261. Доведіть, що квадрат натурального числа має непарну кількість дільників.
ЗАВДАННЯ № 7 «ПЕРЕВІРТЕ СЕБЕ» В ТЕСТОВІЙ ФОРМІ
1. Яка з наведених пар чисел є розв’язком рівняння 5x + 3y = 4? А) (2; 1); Б) (1; 0); В) (2; –2); Г) (–1; 2).
2. Які координати точки перетину графіка рівняння 2x – 5y = 10 з віссю абсцис?
А) (0; –2); Б) (–2; 0); В) (0; 5); Г) (5; 0).
5x 4y 11,
3. Розв’яжіть систему рівнянь
2x 4y 10.
А) (3; 1); Б) (1; 3); В) (1; 2); Г) (2; 1).
15x 2y 7,
4. Розв’яжіть систему рівнянь
2x y 6.
А) (3; –19); Б) (1; –4); В) (–5; 41); Г) (–1; 11).
x y 1,
5. Нехай пара чисел (a; b) є розв’язком системи рівнянь
2 2 3x y 7.
Знайдіть значення виразу a – b .
А) 5; Б) –5; В) 3; Г) –3.
3x y 4,
6. При якому значенні a система рівнянь не має
x ay 6
розв’язків?
А) 3; Б) –3; В) ![]() ; Г) −
; Г) −![]() .
.
4x by 10, 7. При якому значенні b система рівнянь має безліч розв’язків? 2x 3y 5
А) –6; Б) 6; В) 3; Г) такого значення не існує.
8. Графік лінійної функції проходить через точки A (1; 4) і B (–2; 13). Задайте цю функцію формулою.
А) y = 3x + 1; В) y = –3x + 1;
Б) y = –3x + 7; Г) y = 3x + 7.
9. Мати й донька зліпили разом 208 вареників, причому донька працювала 2 год, а мати — 3 год. За 1 год мати робить на 16 вареників більше за доньку.
Нехай донька за 1 год робить x вареників, а мати — y вареників. Яка з наведених систем рівнянь є математичною моделлю ситуації, описаної в умові?
2x 3y 208, 2x 3y 208,
А) В) x y 16; y x 16;
3x 2y 208, 3x 2y 208,
Б) Г)
x y 16; y x 16.
завдання № 7 «Перевірте себе» в тестовій формі
![]()
10. Із двох міст, відстань між якими 60 км, виїхали одночасно вантажний і легковий автомобілі. Якщо вони рухатимуться назустріч один одному, то зустрінуться через 30 хв. Якщо вони рухатимуться в одному напрямі, то легковий автомобіль наздожене вантажний через 3 год після початку руху.
Нехай швидкість вантажного автомобіля дорівнює x км/год, а легкового — y км/год. Яка з наведених систем рівнянь відповідає умові задачі?
|
0,5x А) 3y |
0,5y 60,
3x 60; |
30x В) 3x |
30y 60, 3y 60; |
|
30x Б) 3y |
30y 60,
3x 60; |
0,5x Г) 3x |
0,5y 60, 3y 60. |
11. Люстра та настільна лампа коштували разом 2000 грн. Після того як люстра подорожчала на 10 %, а настільна лампа подешевшала на 10 %, вони стали коштувати разом 2020 грн.
Нехай люстра коштувала спочатку x грн, а настільна лампа — y грн. Яка з наведених систем рівнянь є математичною моделлю ситуації, описаної в умові задачі?
x y 2000, x y 2000,
А) В)
110x 90y 2020; 0,1x 0,1y 2020; x y 2000, x y 2000,
Б) Г)
1,1x 0,9y 2020; 0,9x 1,1y 2020.
12. Розв’яжіть рівняння x2 + y2 + 12x – 2y + 37 = 0.
А) (6; 1); В) (–6; –1);
Б) (–6; 1); Г) рівняння не має розв’язків.
ГОЛОВНЕ В ПАРАГРАФІ 4
Розв’язок рівняння з двома змінними
Пару значень змінних, яка перетворює рівняння в правильну рівність, називають розв’язком рівняння з двома змінними.
Розв’язати рівняння з двома змінними
Розв’язати рівняння з двома змінними — це означає знайти всі його розв’язки або показати, що воно не має розв’язків. Властивості рівнянь із двома змінними
¤ ![]() Якщо до обох частин даного рівняння додати (або від обох частин відняти) одне й те саме число, то отримаємо рівняння, яке має ті самі розв’язки, що й дане.
Якщо до обох частин даного рівняння додати (або від обох частин відняти) одне й те саме число, то отримаємо рівняння, яке має ті самі розв’язки, що й дане.
¤ ![]() Якщо будь-який доданок перенести з однієї частини рівняння в другу, змінивши при цьому його знак на протилежний, то отримаємо рівняння, яке має ті самі розв’язки, що й дане.
Якщо будь-який доданок перенести з однієї частини рівняння в другу, змінивши при цьому його знак на протилежний, то отримаємо рівняння, яке має ті самі розв’язки, що й дане.
¤ ![]() Якщо обидві частини рівняння помножити (поділити) на одне й те саме відмінне від нуля число, то отримаємо рівняння, яке має ті самі розв’язки, що й дане.
Якщо обидві частини рівняння помножити (поділити) на одне й те саме відмінне від нуля число, то отримаємо рівняння, яке має ті самі розв’язки, що й дане.
Графік рівняння з двома змінними
Графіком рівняння з двома змінними називають геометричну фігуру, що складається з усіх тих і тільки тих точок координатної площини, координати яких (пари чисел) є розв’язками даного рівняння.
Лінійне рівняння з двома змінними
Рівняння виду ax + by = c, де x і y — змінні, a, b, c — деякі числа, називають лінійним рівнянням із двома змінними.
Графік лінійного рівняння з двома змінними
У кожному з двох випадків: 1) b ≠ 0; 2) b = 0 і a ≠ 0 — графіком рівняння ax + by = c є пряма.
Графіком рівняння 0x + 0y = 0 є вся координатна площина.
Розв’язок системи рівнянь із двома змінними
Розв’язком системи рівнянь із двома змінними називають пару значень змінних, яка перетворює кожне рівняння системи в правильну рівність.
Розв’язування системи лінійних рівнянь методом підстановки
1) Виразити з будь-якого рівняння системи одну змінну через другу;
2) підставити в інше рівняння системи замість цієї змінної вираз, отриманий на першому кроці;
Головне в параграфі 4
3) розв’язати рівняння з однією змінною, отримане на другому кроці;
4) підставити знайдене значення змінної у вираз, отриманий на першому кроці;
5) обчислити значення другої змінної; 6) записати відповідь.
Розв’язування системи лінійних рівнянь методом додавання
1) Дібравши «вигідні» множники, перетворити одне чи обидва рівняння системи так, щоб коефіцієнти при одній зі змінних стали протилежними числами;
2) додати почленно ліві й праві частини рівнянь, отриманих на першому кроці;
3) розв’язати рівняння з однією змінною, отримане на другому кроці;
4) підставити знайдене на третьому кроці значення змінної в будь-яке з рівнянь вихідної системи; 5) обчислити значення другої змінної; 6) записати відповідь.
ВПРАВИ ДЛЯ ПОВТОРЕННЯ КУРСУ АЛГЕБРИ 7 КЛАСУ
1262. Заповніть таблицю:
|
|
a |
–2 |
–1 |
–0,5 |
0 |
0,5 |
1 |
2 |
||
|
|
a3 – a2 |
|
|
|
|
|
|
|
||
|
|
a4 + a2 |
|
|
|
|
|
|
|
||
|
1263. Подайте у вигляді степеня вираз: |
|
|
||||||||
|
1) (a8)4; 4) (a5)5; 7) a6a6a6; |
10) (a4)5 : a7; |
|
||||||||
|
2) a8a4; 5) a2a3a4; 8) (a6a6)6; |
11) (a2)9 : (a6)3; |
|
||||||||
|
3) a5a5; 6) (a2)3 a4; 9) (a6)6 a6; |
12) (a8a7) : a14. |
|
||||||||
1264. При якому значенні x є правильною рівність:
1) 5xæ56 = 524; 2) (3m)x = 35m; 3) 2xæ2m = 26m; 4) (4x)3m = 46m2, де m — натуральне число?
1265. Чи є тотожно рівними вирази:
1) –a2 і (–a)2; 4) 9aæa2 і (3a)2æa;
2) –a3 і (–a)3; 5) (a4)3 і (a2)6;
3) (a3)2 і a5; 6) (2a)3æ(0,5a)2 і 2a4a?
1266. Подайте у вигляді степеня вираз та обчисліть його значення:
1) 81æ32; 2) 43æ82; 3) 1002æ10003.
1267. Порівняйте значення виразів:
1) 155æ26 і 25æ156; 2) 25æ33æ54 і 24æ35æ53. 1268. Порівняйте значення виразів:
|
1) 1020 і 10110; 1269. Спростіть вираз: |
2) 1015 і 99905. |
1) 4aæ(−3ab); 5) −14b2c8d 9æ1![]() b6d 3;
b6d 3;
2) −2m 2æ0,1m 4næ(−5n 3); 6) ![]() a 4cæ(−12a 2c3)æ1,8a 4b5;
a 4cæ(−12a 2c3)æ1,8a 4b5;
|
3) 0,3a2b4æ1,2a4b; |
7) 3x6æ(–4x2y)2; |
|
4) –6x3y6æ1,5xy; |
8) (–xy)3æ(–2x2y2)4. |
1270. Подайте даний одночлен A у вигляді Bn, де B — деякий одночлен, якщо:
1) A = a6b9, n = 3; 3) A = 81a2b4c8, n = 2;
2) A = 32a10, n = 5; 4) A = –8a12b18, n = 3.
1271. Спростіть вираз:
1) 4a3ab – 6a2b3b3 – 5abæ3a + 7a3bæ0,2b4;
2) 11m2æ2mn – 9mnæ6mn3 + 10mnm;
3) 8xx 4xæ ![]() xy 18xyæ
xy 18xyæ![]() yx 5;
yx 5;
4) 9x3xy2 – 8xy2y8 + 12x2yæ4y – 0,4xy3æ6x3y2.
1272. Знайдіть суму та різницю многочленів:
1) ![]()
![]()
![]() 2,8b −0,75b2 і 1 b2 −1b; 2) 12 x 2 +2y і 2 3 x 2 −1y.
2,8b −0,75b2 і 1 b2 −1b; 2) 12 x 2 +2y і 2 3 x 2 −1y.
4714
1273. Доведіть, що значення виразу 3x 2 −9x −(8 −5x 2 −(9x −8x 2)) не залежить від значення змінної.
1274. Який многочлен треба додати до многочлена a4 – b4 + a3 – – b3 – 3ab, щоб їхня сума тотожно дорівнювала многочлену b4 + 2ab?
1275. Який многочлен треба відняти від многочлена 3c5 – 2c4 + + 14c3 – 4c2 + c, щоб їхня різниця тотожно дорівнювала многочлену 5c3 + c2 – 7c?
1276. Який многочлен треба додати до многочлена m3 – m2n + mn2 – n4, щоб їхня сума тотожно дорівнювала 5?
1277. Чи існують такі значення x і y, при яких многочлени –4x2 – – 12xy + 7y2 і 6x2 + 12xy – 5y2 одночасно набувають від’ємних значень?
1278. Знайдіть значення виразу:
1) 2a (3a – 5) – 4a (4a – 5), якщо a = –0,2;
2) 7ab (2a – 3b) + 2a (3ab + 10b2), якщо a = –3, b = 5; 3) 2a4 (3a2 + a – 8) – 6a6, якщо a = –1.
1279. Розв’яжіть рівняння:
3x 1 x 5 2x ; 4) 2x 2x 1 3x 9;
1)
6 3 9 3 6 4
2) 3x 1 5x 3 2x ; 5) 9x 7 9x 13 3 x ;
2 4 3 4 8 2
3) x 5 1 x 2x 1; 6) 6x 7 5x 8 3.
8 2 3 6 9
1280. Розв’яжіть рівняння:
1) 3x (4x – 1) – 6x (1,5 + 2x) = 4,8;
2) 0,2x (5x – 8) + 3,6 = x (x – 0,7);
3) x (9x – 4) – 3x (3x – 1) = 8 – x; 4) 18x2 – 6x (3x + 2) = –12x.
1281. Доведіть тотожність:
1) 0,2x 3 (2,5x 4) (6 x 2) 0,5x 6 0,8x 5 3x 4 4,8x 3; 2) (a 2) (a 2 3a 18) (a 3) (a 2 4a 12).
1282. Яке число можна підставити замість a, щоб рівність
(5x + a) (x – 2) = 5x2 – 7x – 2a
була тотожністю?
1283. Яке число можна підставити замість b, щоб рівність
(3x + b) (x + 3) = 3x2 + 5x + 3b
була тотожністю?
1284. Розкладіть на множники:
1) 1 a 6 − 1 a 2b; 3) x3y2z5 – 2xy5z3 + 3x2y3z;
2 4
2) 5m2n3k4 + 35m4n3k2; 4) a2nb3n – anb4n, де n — натуральне число. 1285. Обчисліть, використовуючи винесення спільного множника за дужки, значення многочлена:
1) a2 + 4,72a – 32,8, якщо a = 5,28;
2) 12,3x – 12,3y + 4,7, якщо x = 8,14, y = 8,04.
1286. Обчисліть, використовуючи винесення спільного множника за дужки:
1) 2,49æ1,35 1,35æ1,84 1,352;
2) 0,252æ1,6 0,25æ1,62 0,25æ1,6æ0,85; 3) 3,24æ18,7 3,24æ16,4 2,3æ6,76; 4) 5,12æ9,76 5,12æ5,36 5,122.
1287. Доведіть, що значення виразу:
1) 173 + 172 – 17 кратне 61;
2) 254 – 1252 кратне 40;
3) 66 – 183 кратне 42;
4) 5æ2962 3æ2961 2960 кратне 60. 1288. Доведіть, що число:
1) abba ділиться націло на 11;
2) ![]() aaabbb ділиться націло на 37;
aaabbb ділиться націло на 37;
3) ababab ділиться націло на 7;
4) abab−baba ділиться націло на 9 і на 101.
1289. При якому значенні a рівняння
(x + 2) (x – 4) – (x – 2) (x + 4) = ax
має безліч коренів?
1290. При якому значенні a рівняння
(3x – 1) (x + a) = (3x – 2) (x + 1)
не має коренів?
1291. Розкладіть на множники:
1) xm – xn + ym – yn; 5) 6ab2 – 3b2 + 2a2b – ab;
2) 3a – 3b + ac – bc; 6) 2c3 – 5c2d – 4c + 10d;
3) 9a – ab – 9 + b; 7) x3y2 – x + x2y3 – y;
4) a5 + a3 + 2a2 + 2; 8) ax2 – ay – cy + bx2 + cx2 – by. 1292. Обчисліть значення виразу:
1) 1,662 +1,66æ4,68 +2,342; 2) 1,042 1,04æ1,28 0,642.
![]()
1293.* При яких значеннях a, b, c і d виконується рівність abæcd =
![]()
= adæcb?
1294. Спростіть вираз:
1) 6x2 + (2y – 3x) (2y + 3x);
2) (a + 2) (a – 3) – (4 – a) (a + 4);
3) (5 – 2x) (5 + 2x) – (3 – 2x) (4 – 2x);
4) (2ab + 1) (2ab – 1) (16a4b4 + 1) (4a2b2 + 1).
1295. Обчисліть значення добутку, використовуючи формулу (a b) (a b) a 2 b2:
1) 19æ21; 2) 98æ102; 3) 2![]() æ3
æ3![]() ; 4) 7,9æ8,1.
; 4) 7,9æ8,1.
1296. Розв’яжіть рівняння:
1) 4x (7 + 9x) – (6x + 5) (6x – 5) = 39;
2) (x – 8) (x + 10) – (x + 7) (x – 7) = 5x – 31.
1297. Доведіть, що значення виразу
(a + b – c) (a – b) + (b + c – a) (b – c) + (c + a – b) (c – a) тотожно дорівнює нулю.
1298. Знайдіть значення виразу:
1) 432 −232; 2) 2562 −2442; 3) 7,22 −2,82.
1299. Обчисліть:
1) 329422 −−132322 ; 2) ![]() 2,56,5322 −−10,,78252 .
2,56,5322 −−10,,78252 .
1300. Розв’яжіть рівняння:
1) 36x2 – (3x – 27)2 = 0; 2) (4x – 7)2 – (2x + 17)2 = 0.
1301. Доведіть, що при будь-якому натуральному значенні n значення виразу:
1) (4n + 19)2 – (3n – 5)2 ділиться націло на 7; 2) (2n + 5)2 – (2n – 3)2 ділиться націло на 16.
1302. Доведіть, що при будь-якому натуральному значенні n значення виразу (n 2 3n 1)2 n 4 8n 2 3n 5 кратне 6.
1303. Доведіть, що при будь-якому натуральному значенні n значення виразу 16n 4 (4n 2 2n 1)2 8n 1 кратне 4.
1304. При якому значенні a рівняння (a – 3) (a + 5) x = a2 – 9:
1) має безліч коренів; 2) не має коренів; 3) має один корінь?
1305. Використовуючи формулу квадрата суми або формулу квадрата різниці, обчисліть:
|
1) 692; |
3) 522; |
5) 2992; |
|
2) 912; |
4) 97 2; |
6) 10,22. |
1306. На скільки значення виразу (3a2 – 2)2 – (3a2 –1) (3a2 + 1) + 12a2 більше за число 2?
1307. Доведіть, що не існує натурального значення n, при якому значення виразу (8n + 5) (2n + 1) – (4n + 1)2 ділилося бл націло на 5.
1308. Чи існує таке натуральне значення n, при якому значення виразу (2n – 3) (2n + 3) – (n + 3)2 не ділилося б націло на 3?
1309. Розв’яжіть рівняння:
1) 3 (x 7)2 2 (x 7) (x 2) (x 11) (x 4) 101; 2) 2x (x 3)2 3x (x 1) (x 8) x 2 ( x 9) 21; 3) y (2y 5) (2y 5) 4y (y 6)2 13 48y 2.
1310. Подайте у вигляді квадрата двочлена вираз:
1) (a + 4)2 – 2 (a + 4) + 1; 3) (3y + 8)2 + (4y + 6)2 + 4y; 2) (3b + 2)2 + 4 (3b + 2) + 4; 4) (x – 5y)2 + (x + 12y)2 – x (x – 12y).
1311. Суму якого одночлена та тричлена 4a2 – 6ab + 9b2 можна розкласти на множники за формулою квадрата двочлена? Знайдіть ще три таких одночлени.
1312. Доведіть, що не має коренів рівняння:
1) x2 – 8x + 18 = 0; 2) x2 + x + 1 = 0. 1313. Розкладіть на множники:
1 a 8 −b6; 3) x21y24 – m12n15;
1)
64
2) a3b6c9 + 8; 4) a6b6 + 1.
1314. На скільки значення виразу 27a3 + 4 – (9a2 – 3a + 1) (3a + 1) менше від числа 10?
1315. Розв’яжіть рівняння:
1) (x – 2) (x2 + 2x + 4) = x3 + 24x;
2) (3 – 2x) (9 + 6x + 4x2) – 2x (5 – 2x) (5 + 2x) = 7.
1316. Чи ділиться значення виразу 373 + 233 націло на 60?
1317. Чи ділиться значення виразу 6543 – 5543 націло на 200?
1318. Розкладіть на множники:
1) (a – b) (a + b) – c (c – 2b); 2) (b – c) (b + c) – a (a + 2c).
1319. З поданих чотирьох виразів лише три можна розкласти на множники. Знайдіть ці вирази та розкладіть їх на множники:
1) 9mx – 6nx + 6my – 4ny; 3) x2 – 4x + y2 + 2y + 5; 2) 36x2 – 24x + 4 – y2; 4) 4a + 3 + a2 + 2b – b2.
1320. Подайте у вигляді добутку чотирьох множників вираз: 1) a5 – a4 – 16a + 16;
2) a2nb2n – b2n – a2n + 1, де n — натуральне число.
1321. Знайдіть значення виразу:
1) 1,87 2 1,132 6æ1,13; 3) 0,793 +3æ0,79æ0,21 +0,213.
2) 1,6283 −1,2æ1,628æ1,228 −1,2283;
1322. Доведіть, що значення виразу 1710 3æ7 24 3æ7 25 17 9 ділиться націло: 1) на 18; 2) на 36.
1323. Доведіть, що різниця куба натурального числа та самого цього числа ділиться націло на 6.
1324. Доведіть, що сума добутку трьох послідовних натуральних чисел і середнього із цих чисел дорівнює кубу середнього числа.
1325. Нехай x + y = a, xy = b. Доведіть, що:
1) x2 + y2 = a2 – 2b;
2) x3 + y3 = a3 – 3ab;
3) x4 + y4 = a4 – 4a2b + 2b2.
1326.* Доведіть, що при будь-якому натуральному значенні n значення виразу n (n + 1) (n + 2) (n + 3) + 1 дорівнює квадрату деякого натурального числа.
1327.* Доведіть, що при будь-якому натуральному значенні n значення виразу n (n + 2) (n + 4) (n + 6) + 16 дорівнює квадрату деякого натурального числа.
1328.* Доведіть, що різниця між квадратом натурального числа, яке не кратне 3, і числом 1 кратна 3.
1329.* Доведіть, що при будь-якому натуральному значенні n, яке не кратне 5, значення виразу n4 – 1 ділиться націло на 5.
1330.* Чи можна стверджувати, що значення виразу n3 + 2n ділиться націло на 3 при будь-якому натуральному значенні n?
1331.* Доведіть, що при будь-якому натуральному значенні n значення виразу n7 −n кратне 42.
1332. Дано функції f (x) = x2 – 2x і g (x) x 2 . Порівняйте:
x
1) f (2) і g (–1); 2) f (0) і g (2); 3) f (1) і g (1).
1333. Функцію задано таблично:
|
x |
5 |
3 |
1 |
–1 |
–3 |
|
y |
3 |
1 |
–1 |
–3 |
–5 |
Задайте цю функцію описом і формулою.
1334. При всіх додатних значеннях аргументу значення функ-ції f дорівнює –1, при всіх від’ємних — дорівнює 1, а f (0) = 0.
Побудуйте графік функції f.
1335. Знайдіть координати точки графіка функції y = 6x – 5: 1) абсциса й ордината якої рівні між собою; 2) сума координат якої дорівнює 30.
1336. При якому значенні a через точку M (3; –2) проходить графік функції:
1) y = ax – 8; 2) y ![]() x a?
x a?
1337. Чи є лінійною функція:
1) f (x) = (x – 1) (x + 1) – x (x – 3);
2) f (x) (2x 3)2 (x 4) (x 2); 3) f (x) (x 3)2 x (x 6)?
У разі ствердної відповіді побудуйте її графік.
1338. Графіки функцій y = (5 – a) x + a і y = ax + 2 перетинаються в точці, абсциса якої дорівнює –3. Знайдіть ординату цієї точки.
1339. Побудуйте графік функції y = 2x + 3. Користуючись графіком, знайдіть значення аргументу, при яких значення функції:
1) дорівнюють 5; 3) менші від 5;
2) більші за 5; 4) більші за –3, але менші від 7.
1340. Не виконуючи побудови графіка функції y = 12x – 6, знайдіть координати:
1) точок перетину графіка з осями координат;
2) точки перетину графіка даної функції з графіком функції y = 6x + 24.
1341. Побудуйте графік функції:
1) y = | x | – 3; 2) y = | x – 3 |.
1342. При якому значенні a пара чисел (a; –a) є розв’язком рівняння:
1) 6x + 5y = 7; 3) x2 – 3y = 0; 2) 8x – 2y = 4; 4) x + | y | = –2?
1343. Побудуйте графік рівняння y + 1,5x = c, якщо він проходить через точку A (–2; 1).
1344. Складіть систему двох лінійних рівнянь із двома змінними, розв’язком якої є пара чисел: 1) (1; 1); 2) (–3; 5).
1345. Розв’яжіть систему рівнянь:
3x 7y 1, 3 (2a 1) 6 (7 b) 51,
1) 3)
6y 5x 16; 2 (a 6) 7 (1 6b) 49;
3x 5y 19, 3x 4 2y 4x3 5 5,
2) 4)
2x 3y 0; 6x 5y 2x y 9.
2 5
1346.* При якому значенні a сума x + y набуває найменшого значення, якщо
2x 3y 2a2 12a 8,
3x 2y 3a 2 8a 12?
1347.* При якому значенні a різниця x – y набуває найменшого значення, якщо:
x 5y a 2 10a 1, 4x y 4a 2 2a 4?
1348. Учні та учениці 7 класу зібралися на екскурсію. Якщо кожен з них здасть на екскурсію 12 грн 50 к., то для її оплати не вистачить 100 грн; якщо кожен внесе 16 грн, то утвориться надлишок у розмірі 12 грн. Скільки учнів та учениць у цьому класі?
1349. По колу, довжина якого дорівнює 100 м, рухаються два тіла. Коли вони рухаються в одному напрямі, то зустрічаються кожні 20 с. Коли вони рухаються в протилежних напрямах, то зустрічаються кожні 4 с. З якою швидкістю рухаються тіла?
1350. Сплавили два злитки. Маса одного з них становила 105 г, і він містив 40 % міді. Маса другого злитка становила 75 г. Знай- діть відсотковий вміст міді в другому злитку, якщо отриманий сплав містить 50 % міді.
1351. Скільки грамів 4 %-го та скільки грамів 10 %-го розчинів солі треба взяти, щоб одержати 180 г 6 %-го розчину?
1352. У першому бідоні було молоко жирністю 3 %, а в другому — вершки жирністю 18 %. Скільки літрів молока та скільки літрів вершків треба взяти, щоб одержати 10 л молока жирністю 6 %?
1353. З одного поля зібрали по 40 ц ячменю з гектара, а з другого — по 35 ц з гектара. Усього було зібрано 2600 ц. Наступного року врожайність першого поля збільшилася на 10 %, другого — на 20 %. У результаті з двох полів разом було зібрано ячменю на 400 ц більше, ніж попереднього року. Знайдіть площу кожного поля.
1354. З одного поля зібрали по 45 ц пшениці з гектара, а з другого — по 40 ц з гектара. Усього було зібрано 1900 ц. Наступного року внаслідок посухи врожайність першого поля зменшилася на 20 %, другого — на 15 %. У результаті з двох полів разом було зібрано пшениці на 330 ц менше, ніж попереднього року. Знайдіть площу кожного поля.
1355. Половину цукерок розфасували в мішечки по 500 г у кожний, а другу половину — у менші мішечки по 300 г у кожний. Усього вийшло 32 мішечки. Якою є маса всіх цукерок?
1356. Сума цифр двоцифрового числа дорівнює 11. Якщо до цього числа додати 63, то отримаємо число, записане тими самими цифрами у зворотному порядку. Знайдіть дане число.
1357. До деякого двоцифрового числа ліворуч і праворуч дописали цифру 1. У результаті отримали число, яке у 21 раз більше за дане. Знайдіть дане двоцифрове число.
1358. Сума двох чисел дорівнює 28, а різниця їхніх квадратів становить 112. Знайдіть ці числа.
5. Функція пряма ... .
6. Третій степінь числа.
9. Усі значення, яких набуває аргумент функції, утворюють область ... .
14. Правило, за допомогою якого за кожним значенням незалежної змінної можна знайти єдине значення залежної змінної.
15. Рівність, правильна при будь-яких значеннях змінних.
18. Вираз, який є сумою кількох одночленів.
20. Числовий множник одночлена, записаного в стандартному вигляді.
21. Французький математик, на честь якого названо сучасну систему координат.
23. Речення, яке розкриває сутність нового терміна.
24. Мухаммед ібн Муса аль-... . По вертикалі:
1. Розв’язок рівняння.
2. Незалежна змінна.
3. Розкладання многочлена на множники методом ... .
4. Добуток рівних множників.
7. Другий степінь числа.
8. Графік лінійної функції.
10. Геометрична фігура, яка складається з усіх тих і тільки тих точок координатної площини, абсциси яких дорівнюють значенням аргументу функції, а ординати — відповідним значенням функції.
11. Одна з координат точки на площині.
12. Вісь ... .
13. Увиразі 74 число 7 — ... степеня.
16. Вираз, який є добутком чисел, змінних та їхніх степенів.
17. Термін, яким позначають процес, що дозволяє за скінченну кількість кроків отримати розв’язок задачі.
19. У виразі an змінна n — ... степеня.
22. Геометрична фігура, яка є графіком рівняння x 2 (y 1)2 0.
ДРУЖИМО З КОМП’ЮТЕРОМ
Пропонуємо вашій увазі завдання з елементами інформатики, які ви зможете виконувати за допомогою комп’ютера в міру вивчення відповідних тем. Деякі з них — продовження та розвиток вправ цього підручника (такі вправи в тексті підручника помічено значком «¿», а тут указано номер відповідної вправи).
На уроках інформатики ви вивчатимете елементи програмування. Головне в програмуванні — це придумати алгоритм, тобто послідовність дій, за допомогою якої можна із вхідних даних отримати вихідні дані. Нижче наведено багато завдань на складання алгоритмів. Ці завдання не є обов’язковими для виконання, їх насамперед адресовано тим, хто цікавиться інформатикою. Якщо ви вже опановуєте якусь мову програмування, то зможете не лише придумати алгоритм, а й написати програму для його реалізації. Якщо ж ви захоплюєтеся програмуванням, то постарайтеся зробити це для всіх наведених тут завдань, хоча серед них є і досить складні. Найскладніші завдання, які потребують багато часу, позначено зірочкою. Їх можна виконати на канікулах.
До п. 1 «Вступ до алгебри»
Як використовують змінні в програмуванні? Чому використання змінних дає змогу розв’язати не одну-єдину задачу, а низку схожих задач?
Дізнайтеся, яку мову програмування ви вивчатимете на уроках інформатики. Як у цій мові використовують змінні? Як складають числові вирази?
Якщо вираз містить ділення на змінну, то чи завжди він має зміст? Як треба це враховувати під час написання програм?
До п. 2 «Лінійне рівняння з однією змінною»
Запишіть алгоритм, для якого вхідними даними є значення чисел a і b, а вихідними — розв’язок лінійного рівняння ax = b. Які випадки треба передбачити, щоб цей алгоритм видавав правильну відповідь для будь-яких значень a і b?
До п. 3 «Розв’язування текстових задач»
Деякі задачі цього пункту схожі. Це означає, що їхня математична модель однакова.
Знайдіть такі задачі. Побудуйте для них математичну модель і напишіть алгоритм для їхнього розв’язування. Які величини будуть для цього алгоритму вхідними даними, а які — вихідними?
До п. 4 «Тотожно рівні вирази. Тотожності»
Чи можна за допомогою комп’ютера довести тотожність, перебравши всі можливі значення змінних, що до неї входять, та обчисливши при цих значеннях змінних значення лівої та правої частин тотожності?
154. Знайдіть в Інтернеті інформацію про те, які загальновідомі фізичні явища А. Цельсій і Г. Фаренгейт поклали в основу своїх температурних шкал.
До п. 5 «Степінь з натуральним показником»
Запишіть алгоритм, вхідними даними для якого є основа степеня a і показник степеня n, а вихідними — степінь числа a з показником n. Для якого значення показника треба розглянути окремий випадок?
До п. 6 «Властивості степеня з натуральним показником»
Напишіть програму, яка ілюструє одну з властивостей степеня з натуральним показником.
До п. 7 «Одночлени»
Як у мові програмування, яку ви вивчаєте, записати одночлен? Що для цього потрібно, крім чисел і змінних? Яка принципова відмінність існує між записами одночлена в математиці та в програмуванні?
Придумайте який-небудь одночлен. Напишіть програму для обчислення його значення. Які величини будуть вхідними даними для цієї програми, а які — вихідними?
До п. 8 «Многочлени»
Як у мові програмування, яку ви вивчаєте, записати многочлен?
Придумайте який-небудь многочлен. Напишіть програму для обчислення його значення.
Многочлен являє собою вираз. У якому порядку виконуються операції під час обчислення його значення в математиці? А в мові програмування, яку ви вибрали?
До п. 9 «Додавання і віднімання многочленів»
Як використовують дужки у вибраній вами мові програмування? Як вони впливають на порядок обчислення виразів?
![]()
377. У цій задачі використано форму запису числа abc. Напишіть програму, для якої вхідними даними є значення змінних a, b, c,
![]()
а вихідними — значення числа abc. Чи можете ви написати програму, для якої кількість цифр у цьому записі буде змінною? До п. 10 «Множення одночлена на многочлен»
Як записати вибраною вами мовою програмування добуток одночлена та многочлена?
До п. 11 «Множення многочлена на многочлен»
Як записати вибраною вами мовою програмування добуток двох многочленів?
дружимо з комп’ютером
468. Сформулюйте цю задачу в загальному вигляді. Які дані для цієї задачі є вхідними, а які — вихідними? Побудуйте математичну модель задачі. Запишіть алгоритм її розв’язування в загальному вигляді.
До п. 12 «Розкладання многочлена на множники.
Винесення спільного множника за дужки»
508. Спростіть вираз, наведений у цій вправі. Виберіть які-небудь значення змінних. Обчисліть за допомогою калькулятора спочатку значення початкового виразу, потім — значення спрощеного виразу. На скільки операцій спрощення виразу полегшило роботу з обчислення його значення?
517. Запишіть алгоритм для розв’язування цієї задачі перебором усіх двоцифрових чисел. Скільки часу знадобилося б для розв’язування цієї задачі перебором без комп’ютера та калькулятора?
523. Запишіть алгоритм для розв’язування цієї задачі перебором усіх двоцифрових чисел.
До п. 13 «Розкладання многочлена на множники.
Метод групування»
550. Сформулюйте цю задачу в загальному вигляді. Які дані для цієї задачі є вхідними, а які — вихідними? Створіть математичну модель задачі. Запишіть алгоритм розв’язування цієї задачі в загальному вигляді.
553. Запишіть мовою програмування, яку ви вивчаєте, наведені в задачі вирази.
До п. 14 «Добуток різниці та суми двох виразів»
577. Напишіть програму для обчислення значення виразу, наведеного в цій задачі. Чи можна за допомогою цієї програми довести твердження задачі?
До п. 15 «Різниця квадратів двох виразів»
595. Чи можете ви сформулювати алгоритм, яким користувалися під час розв’язування цієї задачі?
606. Запишіть алгоритм для розв’язування цієї задачі.
607. Запишіть алгоритм для розв’язування цієї задачі. Яким чином ви задасте число p?
До п. 16 «Квадрат суми та квадрат різниці двох виразів»
656, 657. Чи можна для задач 588 і 589 побудувати спільну математичну модель? Запишіть спільний алгоритм для розв’язування цих задач.
До оповідання «Трикутник Паскаля»
Напишіть програму для формування трикутника Паскаля, вхідними даними для якої є кількість рядків у трикутнику. Зверніть увагу на розташування результатів у формі рівнобедреного трикутника.
До п. 17 «Перетворення многочлена у квадрат суми або різниці двох виразів»
697.° Чи можете ви сформулювати алгоритм, яким користувалися під час розв’язування цієї задачі?
737. Знайдіть в Інтернеті інформацію про те, скільки кілограмів макулатури (у середньому) заміняють одне дерево під час виробництва паперу. Виберіть який-небудь вид дерев і знайдіть кількість кисню, яку виробляє дерево такого виду за рік. За умовою задачі 737 визначте, скільки дерев такого виду врятували учениці й учні цієї школи та який об’єм кисню вироблять ці дерева за рік.
738. За допомогою табличного редактора автоматизуйте обчислення вартості перевезення вантажу за заданими масою вантажу, відстанню його перевезення, вантажопідйомністю автомобіля та вартістю перевезення одним автомобілем на 10 км. Знайдіть засоби табличного редактора, які зведуть відповідь до кількості автомобілів, вираженої цілим числом.
744. Запишіть мовою програмування, яку ви вивчаєте, наведені в задачі вирази.
До п. 18 «Сума й різниця кубів двох виразів»
751.° Запишіть алгоритм, за допомогою якого можна розкласти на множники суму або різницю двох одночленів за формулами суми або різниці кубів двох виразів. Які вхідні дані треба передбачити, щоб цей алгоритм працював для якомога різноманітніших одночленів?
До п. 20 «Зв’язки між величинами. Функція»
Напишіть програму, що ілюструє розв’язування прикладу 2 цього пункту. Які вхідні дані треба передбачити, щоб написана вами програма була якомога гнучкішою (тобто щоб її можна було застосовувати для якомога більшого числа випадків)?
У вправах цього пункту описано різноманітні функціональні залежності між величинами. Виберіть кілька залежностей; для кожної з них визначте незалежну змінну й запишіть алгоритм, для якого вхідними даними буде значення незалежної змінної, а вихідними — значення залежної змінної.
дружимо з комп’ютером
Яким чином можна зобразити координатну площину на екрані комп’ютера? Знайдіть засоби в графічному редакторі, якими ви для цього скористаєтесь. Які засоби використовують у мові програмування, що ви її вивчаєте, для розміщення яких-небудь зображень у певному місці екрана комп’ютера?
843.° Запишіть алгоритм для обчислення залежності об’єму V води в цистерні від часу t, протягом якого з неї виливається вода. Не забудьте, що рано чи пізно вода в цистерні закінчиться. Яку відповідь має видавати цей алгоритм, коли вся вода із цистерни виллється? Зробіть висновок, як потрібно в програмуванні враховувати область визначення функції.
До п. 21 «Способи задання функції»
Створіть у текстовому та/або табличному редакторі таблицю, яка задає деяку функцію.
Вивчіть інструменти цього редактора, які дають змогу заповнити таблицю за допомогою формули, що задає функцію. Виконайте за допомогою цих інструментів які-небудь завдання цього пункту.
До п. 22 «Графік функції»
Освойте інструменти текстового та/або табличного редактора для побудови графіка функції, заданої таблично. Які елементи оформлення дають змогу зробити графік наочним?
Чи знаєте ви які-небудь комп’ютерні програми, що дають змогу побудувати графік довільної функції?
* Ви можете написати свою програму, яка зображує графік довільної функції на екрані комп’ютера. Які інструменти програмування вам потрібно для цього опанувати? Що необхідно знати про цю функцію, щоб графік адекватно зображував її та був красиво розташований на екрані?
До п. 23 «Лінійна функція, її графік і властивості»
Запишіть алгоритм, що за вхідними даними k і b визначить, яка пряма є графіком функції y = kx + b: горизонтальна чи негоризонтальна; проходить ця пряма через початок координат чи ні.
Створіть у текстовому та/або табличному редакторі таблицю, що задає яку-небудь лінійну функцію. За допомогою засобів цього редактора побудуйте графік вибраної функції.
До п. 24 «Рівняння з двома змінними»
Припустимо, що ви маєте підпрограму, вхідними даними для якої є пара чисел, а вихідними — відповідь, чи є ця пара чисел розв’язком деякого рівняння з двома змінними. Як, використовуючи дану підпрограму, написати програму для зображення графіка цього рівняння на екрані комп’ютера? Що ще треба знати, щоб отриманий графік був інформативним?
* Напишіть таку програму.
До п. 25 «Лінійне рівняння з двома змінними та його графік»
Запишіть алгоритм, що за вхідними даними a, b і c визначить, яка фігура є графіком рівняння ax + by + c = 0.
* Напишіть програму, яка за вхідними даними a, b і c рисує на екрані комп’ютера графік рівняння ax + by + c = 0.
1110. Автоматизуйте обчислення за допомогою табличного редактора. Зробіть інформацію про ціну продуктів і наявність знижок змінними величинами (вхідними даними).
До п. 26 «Системи рівнянь із двома змінними. Графічний метод розв’язування системи двох лінійних рівнянь із двома змінними»
Опануйте засоби графічного редактора, які дають змогу зобразити на екрані точку із заданими координатами. Навчіться проводити пряму через дві точки. Виберіть яку-небудь систему рівнянь з даного пункту та проілюструйте її розв’язання графічним методом за допомогою цього інструментарію.
До п. 27 «Розв’язування систем лінійних рівнянь методом підстановки»
* За алгоритмом, описаним у цьому пункті, напишіть програму розв’язування системи з двох лінійних рівнянь із двома змінними методом підстановки. Як у цій програмі потрібно передбачити ситуації, коли система не має розв’язків? має безліч розв’язків?
До п. 28 «Розв’язування систем лінійних рівнянь методом додавання»
* За алгоритмом, описаним у цьому пункті, напишіть програму розв’язування системи з двох лінійних рівнянь із двома змінними методом додавання. Як у цій програмі потрібно передбачити ситуації, коли система не має розв’язків? має безліч розв’язків?
До п. 29 «Розв’язування задач за допомогою систем лінійних рівнянь»
* Припустимо, що задано координати деяких двох точок A і B на координатній площині та через ці точки проведено пряму. Задають абсцису деякої точки C, яка лежить на цій самій прямій. Напишіть алгоритм, що знаходить ординату точки C. Чи завжди цей алгоритм «працюватиме»? Яку ситуацію треба розглянути окремо та яку перевірку для цього потрібно виконати? Які вихідні дані для цієї ситуації має видати алгоритм?
ПРОЄКТНА РОБОТА
Ця рубрика адресована передусім тим, хто бажає навчитися самостійно набувати знань, творчо мислити, формувати, висловлювати та відстоювати свою точку зору, висувати гіпотези, знаходити найбільш раціональні та нестандартні рішення.
Першим кроком, який може допомогти в досягненні цих цілей, є участь у проєктній роботі.
Проєкт — це самостійне дослідження за вибраною темою, яке можна виконувати як індивідуально, так і в групі.
Дамо кілька порад щодо організації роботи над проєктом та оформлення результатів дослідження.
1. Під час вибору теми потрібно враховувати її актуальність, наявність джерел інформації в літературі та інтернет-ресурсів. При цьому дуже важливе ваше бажання проявити себе дослідником у роботі саме над вибраною темою.
2. Роботу починають зі складання попереднього плану, у якому викладають задум та етапи реалізації задуманого. Після ознайомлення з основними джерелами інформації складають остаточний план за допомогою керівника проєкту.
3. Важливо чітко сформулювати цілі дослідження. Їх можна записати, наприклад, у такий спосіб: вивчити, описати, проаналізувати, довести, порівняти тощо.
4. Роботу завершують підбиттям підсумків дослідження, роблять висновки, накреслюють перспективи подальшого вивчення теми.
5. Приблизний обсяг роботи — 10–15 сторінок. Додатково можна додати ілюстративний матеріал.
6. Робота може бути оформлена у вигляді реферату, доповіді, комп’ютерної презентації.
Нижче наведено рекомендований список тем, які можна вибрати для проєктної роботи.
1. Арифметика й алгебра в Стародавньому світі
2. Ігри та стратегії
3. Математичні софізми
4. Математичні фокуси
5. Аліквотні дроби
6. Системи числення
Проєктна робота
7. Порівняння за модулем
8. Ознаки подільності
9. Таємниці простих чисел
10. Що сьогодні вивчає алгебра? Новітні галузі алгебри
11. Здобутки українських учених ХХ століття в новітніх галузях алгебри
12. Математичні основи обчислювальної техніки
13. Що таке обчислювальна математика
14. Роль математики в розвитку авіації та космонавтики
15. Українські вчені — засновники вітчизняної кібернетики
ВІДОМОСТІ З КУРСУ МАТЕМАТИКИ 5–6 КЛАСІВ
ЧИСЛА ТА ДІЇ З НИМИ
1. Основна властивість дробу
Якщо чисельник і знаменник даного дробу помножити на одне й те саме натуральне число, то отримаємо дріб, що дорівнює даному: a = ![]() aæn. b bæn
aæn. b bæn
Якщо чисельник і знаменник даного дробу поділити на їхній спільний дільник, то отримаємо дріб, що дорівнює даному: ![]() aæn = a. bæn b
aæn = a. bæn b
2. Скорочення дробів
Ділення чисельника й знаменника дробу на їхній спільний дільник, відмінний від 1, називають скороченням дробу.
Дріб, чисельник і знаменник якого — взаємно прості числа, називають нескоротним.
Якщо скоротити дріб на найбільший спільний дільник чисельника й знаменника, то отримаємо нескоротний дріб.
3. Зведення дробів до найменшого спільного знаменника
Щоб звести дроби до найменшого спільного знаменника, треба:
1) знайти найменший спільний знаменник даних дробів;
2) знайти додаткові множники для кожного з дробів, поділивши спільний знаменник на знаменники даних дробів;
3) помножити чисельник і знаменник кожного дробу на його додатковий множник.
4. Цілі числа. Раціональні числа
Усі натуральні числа, протилежні їм числа та число 0 називають цілими числами.
Натуральні числа називають цілими додатними числами. Числа –1, –2, –3, ... називають цілими від’ємними числами.
Об’єднавши натуральні числа із цілими від’ємними та нулем, отримаємо цілі числа:
|
|
Цілі числа |
|
|
Цілі від’ємні числа |
0 |
Натуральні числа |
Об’єднавши цілі числа з дробовими, отримаємо раціональні числа:
|
|
Раціональні числа |
|
|
Цілі числа |
|
Дробові числа |
5. Модуль числа
Модулем числа a називають відстань від початку відліку до точки, яка зображує це число на координатній прямій.
Модуль числа a позначають так: | a | (читають: «модуль a»).
Модуль додатного числа дорівнює цьому числу; модуль від’ємного числа дорівнює числу, яке протилежне даному; | 0 | = 0. a, якщо a l0;
![]() a a, якщо a 0.
a a, якщо a 0.
Модуль числа набуває тільки невід’ємних значень. Модулі протилежних чисел рівні: | a | = | –a |.
6. Додавання. Властивості додавання
Числа, які додаються, називають доданками, а результат додавання — сумою.
Від перестановки доданків сума не змінюється:
a b b a — переставна властивість додавання.
Щоб до суми двох чисел додати третє число, можна до першого числа додати суму другого та третього чисел:
(a b) c a (b c) — сполучна властивість додавання.
7. Віднімання. Властивості віднімання
Відняти від числа a число b означає знайти таке число, яке в сумі із числом b дає число a.
Рівність a b c правильна, якщо правильна рівність b c a.
У рівності a b c число a називають зменшуваним, b — від’ємником, c — різницею.
Різниця a −b показує, на скільки число a більше за число b або на скільки число b менше від числа a. Для будь-якого числа a правильні рівності: a 0 a, оскільки 0 a a; a a 0, оскільки a 0 a.
8. Додавання і віднімання дробів
Щоб додати два дроби з однаковими знаменниками, треба додати їхні чисельники, а знаменник залишити той самий.
Щоб відняти два дроби з однаковими знаменниками, треба від чисельника зменшуваного відняти чисельник від’ємника, а знаменник залишити той самий.
Щоб додати (відняти) два дроби з різними знаменниками, треба звести їх до спільного знаменника, а потім застосувати правило додавання (віднімання) дробів з однаковими знаменниками.
9. Додавання раціональних чисел
Щоб додати два числа з різними знаками, треба: 1) знайти модулі доданків;
2) від більшого модуля відняти менший модуль;
3) перед отриманим числом поставити знак доданка з більшим модулем.
Щоб додати два від’ємних числа, треба:
1) знайти модулі доданків;
2) додати модулі доданків;
3) перед отриманим числом поставити знак «–».
Сума двох протилежних чисел дорівнює нулю. Для будь-якого раціонального числа a:
a 0 0 a a.
10. Віднімання раціональних чисел
Щоб знайти різницю двох чисел, можна до зменшуваного додати число, протилежне від’ємнику.
11. Множення. Властивості множення
Добутком числа a на натуральне число b, яке не дорівнює 1, називають суму, що складається з b доданків, кожний з яких дорівнює a: aæb a a a ... a.
b доданк ів
Якщо один із двох множників дорівнює 1, то добуток дорівнює другому множнику:
mæ1 =1æm = m .
Якщо один із множників дорівнює нулю, то добуток дорівнює нулю: mæ0 = 0æm = 0.
Якщо добуток дорівнює нулю, то хоча б один із множників дорівнює нулю.
Від перестановки множників добуток не змінюється:
ab = ba — переставна властивість множення.
Щоб добуток двох чисел помножити на третє число, можна перше число помножити на добуток другого та третього чисел:
(ab) c = a (bc) — сполучна властивість множення.
Щоб число помножити на суму двох чисел, можна це число помножити на кожний доданок і отримані добутки додати:
a (b + c) = ab + ac — розподільна властивість множення відносно додавання.
12. Множення звичайних дробів
Щоби помножити дріб на натуральне число, треба його чисельник помножити на це число, а знаменник залишити без зміни: aæn = ![]() aæn. b b a 0 = 0, 0æa = 0. Вважають, що æ
aæn. b b a 0 = 0, 0æa = 0. Вважають, що æ
b b
Добутком двох дробів є дріб, чисельник якого дорівнює добутку чисельників, а знаменник — добутку знаменників: aæc = ![]() aæc. b d bæd
aæc. b d bæd
Щоби помножити мішані числа, треба спочатку записати їх у вигляді неправильних дробів, а потім скористатися правилом множення дробів.
13. Множення раціональних чисел
Щоби помножити два числа з різними знаками, треба помножити їхні модулі та перед отриманим добутком поставити знак «–».
Щоби помножити два від’ємних числа, треба помножити їхні модулі.
Для будь-якого раціонального числа a: aæ(–1) = –a, (–1)æa = –a.
Якщо добуток ab додатний, то числа a і b мають однакові знаки; якщо добуток ab від’ємний, то числа a і b мають різні знаки.
14. Ділення. Властивості ділення
Поділити число a на число b означає знайти таке число, добуток якого із числом b дорівнює числу a.
Отже, рівність a : b = c правильна, якщо правильна рівність bæc = a.
У рівності a : b = c число a називають діленим, число b — дільником, число c — часткою.
При будь-яких значеннях a правильна рівність a : 1 = a.
Якщо a не дорівнює 0, то справедливі такі рівності:
0 : a = 0; a : a = 1.
На нуль ділити не можна!
15. Подільність натуральних чисел
Якщо натуральне число a ділиться націло на натуральне число b, то число a називають кратним числа b, число b — дільником числа а.
Для будь-якого натурального числа a кожне із чисел aæ1, aæ2, aæ3, aæ4, ... є кратним числа a.
Найменшим дільником будь-якого натурального числа a є число 1, а найбільшим — саме число a.
Серед чисел, кратних a, найбільшого немає, а найменше є — це саме число a.
Якщо кожне із чисел a і b ділиться націло на число k, то й сума a + b також ділиться націло на число k.
Якщо число a ділиться націло на число k, а число b не ділиться націло на число k, то сума a + b також не ділиться націло на число k.
Натуральне число називають простим, якщо воно має тільки два різних дільники: одиницю та саме це число.
Натуральне число, яке має більше ніж два дільники, називають складеним.
Будь-яке складене число можна подати у вигляді добутку простих чисел, тобто розкласти на прості множники.
Якщо найбільший спільний дільник двох натуральних чисел дорівнює 1, то їх називають взаємно простими.
16. Ознаки подільності натуральних чисел
Якщо запис натурального числа закінчується цифрою 0, то це число ділиться націло на 10.
Якщо запис натурального числа закінчується будь-якою цифрою, яка відмінна від 0, то це число не ділиться націло на 10.
Якщо натуральне число поділити на 10, то остача дорівнюватиме числу, яке записане останньою цифрою цього числа.
Якщо запис натурального числа закінчується парною цифрою, то це число ділиться націло на 2.
Якщо запис натурального числа закінчується непарною цифрою, то це число не ділиться націло на 2.
Якщо запис натурального числа закінчується цифрою 0 або цифрою 5, то це число ділиться націло на 5.
Якщо запис натурального числа закінчується будь-якою цифрою, відмінною від цифр 0 і 5, то це число не ділиться націло на 5.
Якщо сума цифр натурального числа ділиться націло на 9, то й саме число ділиться націло на 9.
Якщо сума цифр натурального числа не ділиться націло на 9, то й саме число не ділиться націло на 9.
Якщо сума цифр натурального числа ділиться націло на 3, то й саме число ділиться націло на 3.
Якщо сума цифр натурального числа не ділиться націло на 3, то й саме число не ділиться націло на 3.
17. Ділення з остачею
Остача завжди менша від дільника.
Щоб знайти ділене, треба дільник помножити на неповну частку й додати остачу.
У буквеному вигляді це записують так: a = bq + r,
де a — ділене, b — дільник, q — неповна частка, r — остача, r < b.
18. Ділення звичайних дробів
Щоби поділити один дріб на другий, треба ділене помножити на число, обернене до дільника:
a : c = aæd . b d b c
19. Ділення раціональних чисел
Щоб знайти частку двох чисел з різними знаками, треба модуль діленого поділити на модуль дільника й перед отриманим числом поставити знак «–».
Щоб знайти частку двох від’ємних чисел, треба модуль діленого поділити на модуль дільника.
20. Знаходження дробу від числа
Щоб знайти дріб від числа, можна число помножити на цей дріб.
Щоб знайти відсотки від числа, можна подати відсотки у вигляді дробу й помножити число на цей дріб.
21. Знаходження числа за його дробом
Щоб знайти число за значенням його дробу, можна це значення поділити на цей дріб.
Щоб знайти число за його відсотками, можна подати відсотки у вигляді дробу та поділити значення відсотків на цей дріб.
22. Степінь числа
Степенем числа a з натуральним показником n, більшим за 1, називають добуток n множників, кожний з яких дорівнює a: an = aæaæaæ...æa.
n множ ник ів
Число a при цьому називають основою степеня.
Степенем числа a з показником 1 називають саме число a: a1 = a.
Другий степінь числа називають також квадратом числа. Наприклад, запис a2 читають: «a у квадраті». Третій степінь називають кубом числа, а запис a3 читають: «a в кубі».
Якщо в числовий вираз входить степінь, то спочатку виконують піднесення до степеня, а потім інші дії.
ВИРАЗИ. ФОРМУЛИ. РІВНЯННЯ
23. Числові та буквені вирази
Запис, складений із чисел, знаків арифметичних дій і дужок, називають числовим виразом.
Запис, складений із чисел, букв, знаків арифметичних дій і дужок, називають буквеним виразом.
24. Розкриття дужок
Якщо перед дужками стоїть знак «–», то при розкритті дужок треба опустити цей знак, а всі знаки, які стоять перед доданками в дужках, змінити на протилежні.
Якщо перед дужками стоїть знак «+», то при розкритті дужок треба опустити цей знак, а всі знаки, які стоять перед доданками в дужках, залишити без змін.
25. Зведення подібних доданків
Щоб звести подібні доданки, треба додати їхні коефіцієнти й отриманий результат помножити на спільну буквену частину.
26. Формули
Рівності виду y = 3x, P = 2 (a + b), S = a2 називають формулами.
Рівність s = vt, де s — пройдений шлях, v — швидкість руху, а t — час, за який пройдено шлях s, називають формулою шляху.
27. Рівняння
Коренем рівняння називають значення змінної, при якому рівняння стає правильною числовою рівністю.
Розв’язати рівняння — це означає знайти всі його корені або переконатися, що їх узагалі немає. Тому корінь часто називають розв’язком рівняння.
Щоб знайти невідомий доданок, треба від суми відняти відомий доданок.
Щоб знайти невідоме зменшуване, треба до різниці додати від’ємник.
Щоб знайти невідомий від’ємник, треба від зменшуваного відняти різницю.
Щоб знайти невідомий множник, треба добуток поділити на відомий множник.
Щоб знайти невідоме ділене, треба дільник помножити на частку.
Щоб знайти невідомий дільник, треба ділене поділити на частку.
28. Властивості рівнянь
Якщо до обох частин даного рівняння додати (або від обох частин відняти) одне й те саме число, то отримаємо рівняння, яке має ті самі корені, що й дане.
Якщо дане рівняння не має коренів, то, додавши до обох його частин одне й те саме число, отримаємо рівняння, яке теж не має коренів.
Якщо який-небудь доданок перенести з однієї частини рівняння в другу, змінивши при цьому його знак на протилежний, то отримаємо рівняння, яке має ті самі корені, що й дане.
Якщо обидві частини рівняння помножити (поділити) на одне й те саме відмінне від нуля число, то отримаємо рівняння, яке має ті самі корені, що й дане.
ВІДНОШЕННЯ ТА ПРОПОРЦІЇ
29. Відношення
Частку двох чисел a і b, які не дорівнюють нулю, ще називають відношенням чисел a і b, або відношенням числа a до числа b.
Числа a і b називають членами відношення, число a — попереднім членом відношення, а число b — наступним.
Відношення додатних чисел a і b показує, у скільки разів число a більше за число b, або яку частину число a становить від числа b.
Відношення не зміниться, якщо його члени помножити або поділити на одне й те саме число, яке не дорівнює нулю.
30. Пропорції
Якщо відношення а : b дорівнює відношенню c : d, то рівність а : b = c : d називають пропорцією.
Пропорцію можна записати також у вигляді a = c. b d
Числа a і d називають крайніми членами пропорції, а числа b і c — середніми членами пропорції.
31. Основна властивість пропорції
Добуток крайніх членів пропорції дорівнює добутку її середніх членів:
a c, то ad = bc.
якщо =
b d
Якщо a, b, c і d — числа, які не дорівнюють нулю, і ad = bc, то a c a c. відношення і рівні й можуть утворити пропорцію = b d b d
32. Відсоткове відношення двох чисел
Відсоткове відношення двох чисел — це їхнє відношення, виражене у відсотках. Воно показує, скільки відсотків одне число становить від другого.
Щоб знайти відсоткове відношення двох чисел, треба їхнє відношення помножити на 100 та до результату дописати знак відсотка.
33. Пряма пропорційна залежність
Дві величини називають прямо пропорційними, якщо при збільшенні (зменшенні) однієї з них у кілька разів друга збільшується (зменшується) у стільки ж разів.
Якщо дві величини прямо пропорційні, то відношення відповідних значень цих величин дорівнює одному й тому самому для цих величин числу.
Якщо величини y і x прямо пропорційні, то їхні відповідні знаy чення задовольняють рівність = k, де k — число, стале для даних
x
величин.
КООРДИНАТНА ПЛОЩИНА
![]() 34. Прямокутна система координат
34. Прямокутна система координат
Проведемо на площині дві перпендикулярні координатні прямі так, щоб їхні початки відліку збігалися (рис. 77). Ці прямі називають осями координат, точку O їхнього перетину — початком координат. Горизонтальну вісь називають віссю абсцис і позначають буквою x, вертикальну вісь називають віссю ординат Рис. 77 і позначають буквою y.
Вісь абсцис називають також віссю x, а вісь ординат — віссю y, разом вони утворюють прямокутну систему координат. Площину, на якій задано прямокутну систему координат, називають координатною площиною.
Координатні осі розбивають площину на чотири частини, які називають координатними чвертями та нумерують так, як показано на рисунку 78.
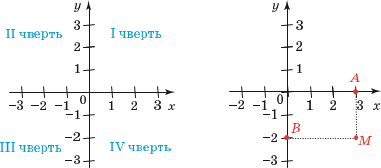
Рис. 78 Рис. 79
На координатній площині позначимо точку M (рис. 79). Пряма, що проходить через точку M перпендикулярно до осі абсцис, перетинає цю вісь у точці A, а пряма, яка перпендикулярна до осі ординат, перетинає цю вісь у точці B. Точка A на осі x має координату 3, а точка B на осі y — координату –2.
Число 3 називають абсцисою точки M, число –2 — ординатою точки M. Числа 3 і –2 однозначно визначають положення точки M на координатній площині. Їх називають координатами точки M і записують: M (3; –2).
Записуючи координати точки, абсцису завжди ставлять на перше місце, а ординату — на друге.
Якщо точка лежить на осі абсцис, то її ордината дорівнює нулю, а якщо точка лежить на осі ординат, то нулю дорівнює її абсциса.
ВІДПОВІДІ ТА ВКАЗІВКИ ДО ВПРАВ
4. 1) 17 ![]() ; 2) 1
; 2) 1![]() ; 3) –0,3; 4) −1
; 3) –0,3; 4) −1![]() ; 5) 1. 5. 1) 11
; 5) 1. 5. 1) 11![]() ; 2) 1
; 2) 1![]() ; 3) 4,4;
; 3) 4,4;
4) −![]() . 23. 110 пудів. 41. 1) 3; 2)
. 23. 110 пудів. 41. 1) 3; 2) ![]() ; 3) коренів немає; 4) коренем рівняння є будь-яке число. 42. 1) 5; 2) 0,8; 3) коренем рівняння є будь-яке число; 4) коренів немає. 43. 1) 0,6; 2)
; 3) коренів немає; 4) коренем рівняння є будь-яке число. 42. 1) 5; 2) 0,8; 3) коренем рівняння є будь-яке число; 4) коренів немає. 43. 1) 0,6; 2) ![]() ; 3) –10; 4) –0,9.
; 3) –10; 4) –0,9.
44. 1) 44; 2) ![]() ; 3) –5,2. 45. 1) −
; 3) –5,2. 45. 1) −![]() ; 2) коренем рівняння є будь-яке число. 46. 1) −
; 2) коренем рівняння є будь-яке число. 46. 1) −![]() ; 2) коренів немає. 47. 1) 0,4; –8; 2) 0; 25; 3)
; 2) коренів немає. 47. 1) 0,4; –8; 2) 0; 25; 3) ![]() ;
;
–12; 4) –0,6; –1; 0,3. 48. 1) 6; –4,5; 2) –0,8; 3. 49. 1) 10; 2) –3.
50. 1) 1; 2) –1,4. 51. 1) 12; 2) 4 ![]() ; 3) 2.
; 3) 2. ![]() ; 2) 2; 3) 4,8. 53. 1) –10; 2) 3; 3) 1; 4) 0,5. 54. 1) –12; 2) –0,2.
; 2) 2; 3) 4,8. 53. 1) –10; 2) 3; 3) 1; 4) 0,5. 54. 1) –12; 2) –0,2. ![]() ; –2; 8) 0; –1. 56. 4) –20; 100; 5) 2,3; –0,9; 6) 0; 4; –4. 57. 2) 55.
; –2; 8) 0; –1. 56. 4) –20; 100; 5) 2,3; –0,9; 6) 0; 4; –4. 57. 2) 55. ![]() .
.
61. 2) –53; –11; –5; –3; 3; 45. 62. 2) 7; 11; 31. 63. 1) 14; 2) ![]() .
.
64. 1) –17; 2) 3,5. 65. 2) 3; 3) 2. 66. 2) 2; 3) –5. 67. 1) a ≠ 5; 2) a ≠ –7.
68. 1) Якщо b ≠ –1, то x 9 ; якщо b = –1, то коренів немає;
b 1
2) x ![]() b24 1. 69. Якщо m ≠ –8, то x = 1; якщо m = –8, то x — будьяке число. 72. 1) 3; 2) –1,8; 3) –1; 2. 73. 1) −
b24 1. 69. Якщо m ≠ –8, то x = 1; якщо m = –8, то x — будьяке число. 72. 1) 3; 2) –1,8; 3) –1; 2. 73. 1) −![]() ; 2) коренів немає.
; 2) коренів немає.
74. 1) a — парне число; 2) a — непарне число; 3) число a кратне 4; 4) таких значень не існує. 75. 1) Число b кратне 3; 2) число b при діленні на 3 дає остачу 1; 3) таких значень не існує. 76. 1) При b > 0; 2) при b < 0. 77. 1) При d < 0; 2) при d > 0. 79. 1) 18 год; перший виконає ![]() завдання, а другий —
завдання, а другий — ![]() завдання. 80. 240 сторінок. 81. 1) Парним; 2) непарним; 3) парним. 82. 1) Ні, 2a < a при a < 0 і 2a = a при a = 0; 2) ні, 2 | a | = | a | при a = 0. 88. 2061 м, 2032 м, 2020 м. 89. 500 м, 400 м, 374 м. 92. 20 робітниць. 93. 90 км.
завдання. 80. 240 сторінок. 81. 1) Парним; 2) непарним; 3) парним. 82. 1) Ні, 2a < a при a < 0 і 2a = a при a = 0; 2) ні, 2 | a | = | a | при a = 0. 88. 2061 м, 2032 м, 2020 м. 89. 500 м, 400 м, 374 м. 92. 20 робітниць. 93. 90 км.
94. 20 кг, 14 кг. 95. 264 місця, 270 місць. 96. 12 км/год, 60 км/год. 97. 28 грн, 16 грн. 98. 7,2 грн. 101. 4 роки. 102. 7 років. 103. 30 словників, 10 словників. 104. 1800 грн, 1200 грн. 105. 11 купюр, 8 купюр. 106. 800 т. 107. 60 грн. 108. 40 кг, 8 кг. 109. 600 кг, 200 кг. 110. 5 днів. 111. 40 л, 80 л. 112. 4,5 год, 0,5 год. 113. 24 хв. 114. 50 км/год, 20 км/год. 115. 30,5 км/год. 116. 2 км/год. 117. 71 турист. 118. 109 апельсинів. 119. 45 кг, 10 кг. 120. 14 кг, 10 кг. 121. 60 книжок. 122. 160 л. 123. 8 днів. 124. 100 задач. 125. 93. 126. 24. 122. 55 км/год, 65 км/год або 70 км/год, 80 км/год. 128. 1) Так; 2) ні. 129. 100 кг, 200 кг. 130. 20 кг, 30 кг. 131. 1) Ні. Вказівка. Нарисуйте два чотирикутники разом з діагоналями. 2) Так. Вказівка. Припустимо, що з міста А неможливо проїхати в місто В. Кожне з них сполучене з чотирма іншими містами. Серед цих двох четвірок міст немає спільних. Отже, у регіоні не менше ніж десять міст. 132. 1) 4,04; 2) –35,16; 3) 1![]() ; 4) −6
; 4) −6 ![]() . 135. 4.
. 135. 4.
136. 3) x — будь-яке невід’ємне число; 4) x — будь-яке недодатне число. 153. 24 год. 155. 1) b < 0; 2) | a | < | b |. 156. Зменшилася на 25 %. 172. 3) 16; 4) 115. 173. 3) 75. 196. 2; 3; 4. 197. 1; 2. 202. 2) x = 1 і y = –2. 204. 1) x = 0; 2) x = 1. 205. 1) x = 0; 2) x = –3. 206. 2) Вказівка. Доведіть, що остання цифра значення виразу дорівнює 0; 3) Вказівка. Значення виразу — це число, остання цифра якого дорівнює 3, а решта — 9. 207. 1) Вказівка. Доведіть, що сума цифр значення виразу дорівнює 9; 2) Вказівка. Доведіть, що остання цифра значення виразу дорівнює 5. 208. 3. 210. 20 %. 211. 60 кг, 20 кг. 212. 1) 3,8; 2) коренів немає. 213. a — від’ємне число, b — додатне число, c = 0. 239. 2) 25; 3) 22n; 4) 2n + 1. 256. 1) 36; 2) 125; –125. 259. 597. 260. 1) 6; 2) 1; 3) 4 або 6; 4) 1, або 3, або 7, або 9. 261. 1) 1; 2) 1; 3) 1 або 9. 262. 1) Вказівка. Останньою цифрою степеня 17 8 є 1; 2) Вказівка. Останньою цифрою степеня 6464 є 6; 3) Вказівка. Останньою цифрою степеня 34n = 81n є 1. 263. 1) Вказівка. Останньою цифрою степеня 440 є 6; 2) Вказівка. Останньою цифрою степеня 2004171 є 4, а степеня 1712004 — 1. 264. 4825 < 4925 =
= 750 < 751 = (73)17 = 34317 < 34417. 266. 12 качок. 267. 3,6 год. 268. 9,6 км. 269. 1) 2; 2) коренем рівняння є будь-яке число. 270. Вказівка. Дане число можна подати у вигляді 1000а + а =
= 1001а. 301. 3) –43,2. 302. 3) −![]() . 303. 2) 24,5; 3) 30. 304. 2) 1350;
. 303. 2) 24,5; 3) 30. 304. 2) 1350;
3) –486. 305. 600 грн. 307. 36 гусей. 327. 600 г, 400 г. 345. 2) 5; 3) коренів немає. 346. 1) 6; 2) коренем рівняння є будь-яке число. 349. 1) –45; 2) 24. 350. 1) 11; 2) ![]() . 365. 5. 373. –9 при x = 0.
. 365. 5. 373. –9 при x = 0.
![]()
374. 4 при y = 0. 378. 1) abc bca cab 100a 10b c 100b 10c a 100c 10a b 111a 111b 111c 111(a b c). 379. Вказівка.
Розгляньте суму даних многочленів. 382. У листопаді. 383. 3990 грн. 384. 4 год. 385. 144 дерева. 386. 10 км. 399. 1) –2; 2) –5; 3) –0,5; 4) коренем рівняння є будь-яке число; 5) коренів немає; 6) 4. 400. 1) 2; 2) 0; 3) 6. 412. 1) 7b2; 2) 0. 413. 1) 45; 2) 0; 3) ![]() ; 4) 2,1;
; 4) 2,1;
5) 3; 6) ![]() ; 7)
; 7) ![]() ; 8)
; 8) ![]() . 414. 1) –1; 2) −
. 414. 1) –1; 2) −![]() ; 3) –4; 4) 10. 415. −
; 3) –4; 4) 10. 415. −![]() .
.
416. 8 см. 417. 64 см. 418. 36 км, 42 км, 30 км. 419. 22 деталі,
34 деталі, 24 деталі. 420. 1) xn + 5 – xn + 1; 2) xn + 4 – x2n + 2 + xn. 421. 1) 5xn + 1; 2) x2n + 2 – 7x. 422. Вказівка. З умови випливає, що a = 3n + 1, b = 9m + 7, де m і n — натуральні числа. 424. 33 коробки. 426. 800 км2, 360 км2, 204,8 км2. 427. 210 сторінок. 429. 90 км. 430. 8 днів. 438. 1) –7; 2) –2; 3) 1; 4) –1; 5) коренів немає. 439. 1) 2; 2) −![]() ; 3) 6; 4) коренем рівняння є будь-яке число. 445. 6; 7; 12; 14.
; 3) 6; 4) коренем рівняння є будь-яке число. 445. 6; 7; 12; 14.
446. 8; 12; 18. 447. 7; 8; 9; 10. 448. 16; 17; 18. 449. 15 см. 450. 18 см, 12 см. 451. 14 см, 12 см. 465. 12 000 грн. 466. 2300 грн. 467. 15 деталей, 11 деталей. 468. 9 %. 469. 1) 3; 2) 9. 471. 60 років. 495. 1) –a (a + b) (2a + 3b); 2) 3m (m – 8) (3m – 16); 3) (a + 5) (3a + 2);
4) (4y – 1) (x – 3); 5) (5m – n)2 (m + 8n)2 (4m – 9n). 496. 1) (x – 6) ×
× (x + 4); 2) (x2 – 2) (2y – 7); 3) (4a – 3b) (3a + 7b); 4) (p – 9)3 ×
× (2p + 1)3 (3p – 8). 497. 1) –7; 2) 2; 2![]() ; 3) 5; –40; 4) 7; 14.
; 3) 5; –40; 4) 7; 14.
498. 1) –6; 9; 2) 10; –6; 3) −![]() ;
; ![]() ; 4) 1
; 4) 1![]() ; 1. 499. 7) 49a2 (1 + 2b)2;
; 1. 499. 7) 49a2 (1 + 2b)2;
8) 81c12 (c – 2)4. 500. 5) 64x2y2 (2x + 5y)2; 6) 32x10 (11x2 – 14y3)5.
505. 1) 0; ![]() ; 2) 0; 0,4; 3) 0; –0,2; 4) 0; 3,6. 506. 1) 0; 6; 2) 0;
; 2) 0; 0,4; 3) 0; –0,2; 4) 0; 3,6. 506. 1) 0; 6; 2) 0; ![]() .
.
507. 1) 2a + 4; 2) 6ab – 4b; 3) 8ab2 −14b3. 508. 1) 2a 2b2; 2) 2ab+2b2.
511. 1) an (a + 1); 2) bn – 3 (b3 – 1); 3) cn – 4 (c6 + 1); 4) dn (dn – 1); 5) 2n +1æ5;
6) 3n + 2 (3n + 1). 512. 1) an (a2 – 1); 2) bn (3b2 – 2b + 1); 3) 25n (1 + + 23n + 4). 513. 2) 24; 3) 20. 514. 2) –4; 3) –12. 515. 1) 1; 2) 0,8; 3) 5.
![]() 516. 1) a = 3; 2) a
516. 1) a = 3; 2) a ![]() . 517. 18. Вказівка. Нехай дане число ab. Тоді
. 517. 18. Вказівка. Нехай дане число ab. Тоді
![]()
ab 10a b (a 1) (b 1), звідси 9a = ab + 1, a (9 – b) = 1. Звідси a = 1, b = 8. 520. 20 кг. 521. 28 банок. 523. Ні. 536. 1) 15; 2) 72; 3) 25. 537. 1) 250; 2) –1. 540. 1) (an + 1) (a + 1); 2) (b + 1) (bn + 1 – 1); 3) (yn + 1 – 1) (3y2 + 5). 541. 1) (x + 6) (x + 2); 2) (x – 4) (x – 1);
3) (x – 1) (x + 8); 4) (x + 1) (x – 5). 542. 1) (x + 1) (x + 3); 2) (x – 2) ×
× (x – 8); 3) (x + 6) (x – 3); 4) (x – 8) (x + 4). 543. Вказівка. n 3 3n 2 2n n n( 2 3n 2) n n( 2 n 2n 2) n n n( ( 1) 2 (n 1))
n n( 1 ) (n 2 ). 544. (a + b + c)2. Вказівка. Подайте кожний із чле-
нів 2ab, 2bc і 2ac даного многочлена у вигляді суми ab + ab, bc + bc, ac + ac відповідно та застосуйте метод групування. 545. Вказівка. 3n 2 2n 2 3n 2n 3n (32 1) 2n (22 1) 3næ10 2næ5 3næ10 2n 1
2 5æ 3næ10 2n 1æ10 10 3( n 2n 1 ). 546. 2. Вказівка. 2x 4 + 3x y2 2 + y 4 y2 2x4 2x y2 2 x y2 2 y 4 y2 2x2 (x 2 y 2) y2 (x 2 y 2 ) y2.
547. Знизилася на 4 %. 548. Знизилася на 23 %. 549. 4 вівці. 550. 6 год. 551. 40 л, 10 л. 569. 5) 16a4 – 1; 6) c12 – 625. 570. 4) a8 – 1. 571. 3) y2n + 4 – x8n; 4) a2n + 2 – b2n –2. 572. 3) 4x2 + 3x + 93; 4) b2c5. 573. 1) x2 – 4x + 19; 2) b12. 574. 1) –1; 2) коренів немає; 3) коренем рівняння є будь-яке число; 4) –25,6. 575. 1) –40; 2) –3. 580. 1) 4; 2) 25; 3) 9; 4) –1; 5) –1. 581. 1) 1; 2) 256. 583. Вказівка. 253æ259 =
= (256 – 3) (256 + 3), 252æ260 = (256 – 4) (256 + 4). 585. 14 км/год, 42 км. 586. 20 кг, 80 кг. 587. 4 год. ![]() 16 807 жмень, 1,34 т.
16 807 жмень, 1,34 т.
![]() ; 2)
; 2) ![]() 1) –150; 2) 12,8. 605. –40. 609. 1) (a – b) ×
1) –150; 2) 12,8. 605. –40. 609. 1) (a – b) ×
× (a + b) (a2 + b2) (a4 + b4); 2) (a2 – 2) (a2 + 2) (a4 + 4) (a8 + 16). 610. 1) 4;
![]() ; 2) –1; –7; 3) –10;
; 2) –1; –7; 3) –10; ![]() ; 2) –16;
; 2) –16; ![]() .
.
615. 1) (2n + 2)2 – (2n)2 – (2n + 2 – 2n) (2n + 2 + 2n) = 2 (4n + 2). 617. 43 і 34. 619. 1) b = 2; 2) b = –2; 3) b ≠ 2 і b ≠ –2. 622. 8 км/год. 623. 45 кг. 624. a = –3. ![]() ; 2) коренем рівняння є будь-яке число. 626. 1) a > 0; 2) a ≠ 0; 3) a — будь-яке число. 653. 5. 654. 1) 9;
; 2) коренем рівняння є будь-яке число. 626. 1) a > 0; 2) a ≠ 0; 3) a — будь-яке число. 653. 5. 654. 1) 9;
2) –0,6; 3) –5. ![]() ; 2) 7. 656. 7 см. 657. 26 см. 658. 12; 13;
; 2) 7. 656. 7 см. 657. 26 см. 658. 12; 13;
14. 659. 19; 20; 21; 22. 670. 1. 671. 0 або 1. 675. 7. 676. 3. 679. a = 1. 680. a ![]() . 683. Нехай n — третє з даних чисел, тоді дані числа дорівнюють відповідно n – 2, n – 1, n, n + 1, n + 2, де n > 2. Доведіть, що сума квадратів цих чисел дорівнює 5 (n 2 +2). Щоб здобутий результат міг бути квадратом деякого натурального числа, значення виразу n2 + 2 має бути кратним 5, тобто його останньою цифрою має бути цифра 0 або цифра 5. Оскільки останньою цифрою значення виразу n2 може бути одна із цифр 0, 1, 4, 5, 6, 9, то значення виразу n2 + 2 не може закінчуватися цифрою 0 або цифрою 5. 684. 5000 т. 686. 500 кг. 687. Однакова. 690. 2) Таких значень немає; 3) x = –1. 705. 1) (4a −b)2; 2) (6x +5y)2. 706. 1) (2m + 2n)2; 2) (7x +4y)2. 707. 1) 0,0016; 2) 10 000. 708. 1) 10 000; 2) 9. 711. 2) −
. 683. Нехай n — третє з даних чисел, тоді дані числа дорівнюють відповідно n – 2, n – 1, n, n + 1, n + 2, де n > 2. Доведіть, що сума квадратів цих чисел дорівнює 5 (n 2 +2). Щоб здобутий результат міг бути квадратом деякого натурального числа, значення виразу n2 + 2 має бути кратним 5, тобто його останньою цифрою має бути цифра 0 або цифра 5. Оскільки останньою цифрою значення виразу n2 може бути одна із цифр 0, 1, 4, 5, 6, 9, то значення виразу n2 + 2 не може закінчуватися цифрою 0 або цифрою 5. 684. 5000 т. 686. 500 кг. 687. Однакова. 690. 2) Таких значень немає; 3) x = –1. 705. 1) (4a −b)2; 2) (6x +5y)2. 706. 1) (2m + 2n)2; 2) (7x +4y)2. 707. 1) 0,0016; 2) 10 000. 708. 1) 10 000; 2) 9. 711. 2) −![]() .
.
712. 2) ![]() . 716. Вказівка. x2 – 14x + 52 = x2 – 14x + 49 + 3 = (x – 7)2 + 3.
. 716. Вказівка. x2 – 14x + 52 = x2 – 14x + 49 + 3 = (x – 7)2 + 3.
717. 1) 1 при x = 3; 2) 16 при x ![]() ; 3)
; 3) ![]() при x
при x ![]() . 719. 1) –8 при x = 2; 2) –1 при x =
. 719. 1) –8 при x = 2; 2) –1 при x = ![]() ; 3) –7 при x
; 3) –7 при x ![]() . 721. 1) 100 при x = –8;
. 721. 1) 100 при x = –8;
2) 11 при x = ![]() . 722. 1) 4 при x = 14; 2) –50 при x
. 722. 1) 4 при x = 14; 2) –50 при x ![]() . 724. (a – 3b) ×
. 724. (a – 3b) ×
× (a – 3b – 4) + 4 = (a – 3b)2 – 4 (a – 3b) + 4 = (a – 3b + 2)2. 725. 6) Вка-
зівка. 2a 2 2b2 (a 2 2ab b2) (a2 2ab b2). 726. 1) (a2 + 1 – a) ×
× (a2 + 1 + a); 2) (x – y) (x + y + 4); 3) (ab – c – 3) (ab + c + 5);
4) (2a + b – 2) (4a – b – 2). 727. 1) (a2 + 4)2 + (3a)2; 2) (x – 5)2 + (y + 7)2; 3) (x – 3y)2 + (x – 3)2; 4) (x – 2)2 – (y + 1)2. 728. 1) x = –4, y = 5; 2) x = –6, y = 1. 729. 1) x = –1, y = 0,5; 2) таких значень не існує. 730. 45. 731. 8. 732. –10. 733. 24 = 12 + 12. Вказівка. Нехай один із доданків дорівнює x, тоді другий дорівнює 24 – x, а їхній добуток: x (24 x) 24x x 2 122 122 2æ12x x 2 144 (12 x)2. 734. 5 см,
5 см. 735. 4. Вказівка. b2 a2 b2 a2 ab ab b a 2 ab. 736. 0.
4 4 2
Вказівка. Обидві частини даної в умові рівності помножте на 2, а потім подайте у вигляді (a – b)2 + (b – c)2 + (a – c)2 = 0. 739. 100 км. 740. 60 га, 40 га. 742. 13. 743. 420 днів. Вказівка. Щоб дізнатися, через скільки днів рибалки знову зберуться на озері разом, треба знайти НСК (1, 2, 3, 4, 5, 6, 7). 764. 1) 9; 2) 25x – 64; 3) –6a2 + 9a – 27; 4) a24 – 1. 765. 1) –124; 2) –y2 + 3y – 36; 3) a6 – b2. 767. 1) 0,5; 2) –1; 3) 8. 768. 1) 6; 2) –5. 774. Вказівка. Нехай дані числа дорівнюють 2n – 1 і 2n + 1. 775. Вказівка. Ці числа можна подати у вигляді 3n + 1 і 3n + 2, де n — довільне натуральне число. 776. 1. Вказівка. x6 + 3x2y2 + y6 = (x2 + y2) (x4 – x2y2 + y4) + 3x2y2.
777. 8. 780. «Модний одяг». 782. 18 кг, 6 кг. 783. 2. 786. 4) ![]() ;
;
6) 0; ![]() . 810. 6) –2; –3; 3; 7) 5; 8) –1; 1. 811. 5) –1; 1; 6) –5;
. 810. 6) –2; –3; 3; 7) 5; 8) –1; 1. 811. 5) –1; 1; 6) –5;
5; 4. 817. 1) (x – y + 4) (x + y – 2); 2) (2a – 3b – 3) (2a + 3b + 1). 818. 1) (5x y 2 4) (5x y 2 10); 2) 4 (3m – 2n + 3) (3m + 2n – 2).
819. 4) (2a – 5) (2a – 1); 5) (3x – 7y) (3x – y); 6) 3 (2m – n) (6m – 7n). 820. 4) (x + 3) (x – 2); 5) (c + 3d) (c + 5d); 6) (3x – 8y) (3x – 2y). 821. 1) –40; 2) 74; 3) 84; 4) 632. 822. 1) 54; 2) 48; 3) 1746. 824. 1) (x – 1) (x + 1) (x – 2) (x + 2); 2) (x2 + x + 1) (x2 – x + 1); 3) (2x2 – 4x + 1) (2x2 + 4x + 1). Вказівка. 4x 4 12x 2 1 (4x 4 4x 2 1) 16x 2;
4) (x2 + x + 1) (x3 – x2 + 1). Вказівка. x 5 x 1 (x 5 x 2) (x 2 x 1);
5) (x2 – 2x + 2) (x2 + 2x + 2); 6) (x – 1) (x + 1) (x2 + 1) (x4 + 2). 825. 1) (x2 – x + 3) (x2 + x + 3); 2) (x2 – 2x – 2) (x2 + 2x – 2). 828. 210 грн. 829. 14, 18, 22. 830. 13 км. 831. 2) –2; 2; –18; 18; 3) –18; 2; 4) 4. 875. a = 3. 876. 420 осіб. 909. Збільшився на 0,8 %.

Рис. 80 Рис. 81
911. 12, 22, 32. 913. Вказівка. Додайте ліві й праві частини даних рівностей. 940. Рис. 80. 941. Рис. 81. 942. 15 год. 947. 15 бджілок. 979. A ![]() ;
; ![]() . 980. 1) (–10; –27); 2) (–14; 8). 981. (3; 5). 985. 1. 986. 3.
. 980. 1) (–10; –27); 2) (–14; 8). 981. (3; 5). 985. 1. 986. 3.
987. k = 0,5, b = 4. 988. k = ![]() , b = –1. 993. 1) n; 2) k; 3) m; 4) p.
, b = –1. 993. 1) n; 2) k; 3) m; 4) p.
995. k = –1. 996. b = 11. 1003. 1) y = x + 3; 2) y = –0,5x – 1. 1004. 1) y ![]() x; 2) y = 2x – 4. 1005. Рис. 82. 1006. Перший —
x; 2) y = 2x – 4. 1005. Рис. 82. 1006. Перший —
![]()
![]()
![]() 360 000 грн, другий — 600 000 грн, третій — 840 000 грн. 1007. 1) –39; 2) –12. 1008. 1)
360 000 грн, другий — 600 000 грн, третій — 840 000 грн. 1007. 1) –39; 2) –12. 1008. 1) ![]() ; 2) 1,4. 1009. Вказівка. Нехай друге із цих чисел дорівнює n, тоді перше число дорівнюватиме n – 1, а третє — n + 1. Розкладіть на множники суму кубів першого та третього чисел. 1011. a2 – b2. Вказівка. x4 + x2y2 + y4 = x4 + + 2x2y2 + y4 – x2y2 = (x2 + y2)2 – x2y2. 1012. З означення модуля випливає, що x lx, тому x −x l0. Разом з тим 2x – x2 – 2 = –x2 + + 2x – 1 – 1 = –(x – 1)2 – 1 < 0. 1024. 2. 1025. 6. 1026. 3) (–3; 0); (3; 0); (0; –3); (0; 3); 4) (5; 0); (–5; 0); (0; –5). 1041. 1) (1; 1); 2) (1; 3); (6; 2); (11; 1). 1044. 3 способи. 1045. 9 задач з алгебри та 2 з геометрії, або 6 задач з алгебри та 4 з геометрії, або 3 задачі з алгебри та 6 з геометрії. 1046. 1) (0; 2); 2) (–1; 3); 3) (–0,5; –0,5); 4) розв’язків немає. 1047. 1) (5; –5); 2) розв’язків немає. 1048. (0; 0); (–1; 0); (1; 0); (0; –2). 1049. (0; 4); (0; –4); (5; 0); (–5; 0). 1050. 5 %.
; 2) 1,4. 1009. Вказівка. Нехай друге із цих чисел дорівнює n, тоді перше число дорівнюватиме n – 1, а третє — n + 1. Розкладіть на множники суму кубів першого та третього чисел. 1011. a2 – b2. Вказівка. x4 + x2y2 + y4 = x4 + + 2x2y2 + y4 – x2y2 = (x2 + y2)2 – x2y2. 1012. З означення модуля випливає, що x lx, тому x −x l0. Разом з тим 2x – x2 – 2 = –x2 + + 2x – 1 – 1 = –(x – 1)2 – 1 < 0. 1024. 2. 1025. 6. 1026. 3) (–3; 0); (3; 0); (0; –3); (0; 3); 4) (5; 0); (–5; 0); (0; –5). 1041. 1) (1; 1); 2) (1; 3); (6; 2); (11; 1). 1044. 3 способи. 1045. 9 задач з алгебри та 2 з геометрії, або 6 задач з алгебри та 4 з геометрії, або 3 задачі з алгебри та 6 з геометрії. 1046. 1) (0; 2); 2) (–1; 3); 3) (–0,5; –0,5); 4) розв’язків немає. 1047. 1) (5; –5); 2) розв’язків немає. 1048. (0; 0); (–1; 0); (1; 0); (0; –2). 1049. (0; 4); (0; –4); (5; 0); (–5; 0). 1050. 5 %.
1051. 20 яблук. 1052. 1) 6; 2) –5.
Рис. 82
1053. 269,5 км. 1055. 1) 12; 2) −![]() . 1097. –12. 1098. –4. 1099. a = –4, b = 2. 1102. 1) d; 2) c; 3) b; 4) a. 1105. 1) y = 0,5x + 2; 2) y = 0,6x – 3. 1106. x + y = 6. 1109. 1 пара (3; 2). 1110. «Апетит». 1112. 24 год.
. 1097. –12. 1098. –4. 1099. a = –4, b = 2. 1102. 1) d; 2) c; 3) b; 4) a. 1105. 1) y = 0,5x + 2; 2) y = 0,6x – 3. 1106. x + y = 6. 1109. 1 пара (3; 2). 1110. «Апетит». 1112. 24 год.
1114. 1) 5; 2) 3,5. 1115. 2) (x – 3y – 4) (x – 3y + 4); 4) (c – b – 3) × × (c + b + 1). 1127. 1) a = 3, b = –2,5; 2) a = 4, b = –6. 1128. a = 2, b = 5. 1133. При a ≠ 7. 1134. 1) 16; 2) –5. 1135. 1) При a ≠ 14; 2) при a = –10. 1138. 1) (–2; 2); 2) (–2; 2); (1; 1); 3) розв’язків немає; 4) (1; –1); (3; 3). 1139. 1) (1; 1); (–3; 3); 2) (2; 1); (–2; –1); 3) (2; 0); (–2; 0); (0; 2); (0; –2). 1141. 3 кг. 1142. 60 км/год. 1143. 3; 5; 7; 9. Вказівка. Позначте найменше із цих чисел 2k – 3, де k — довільне натуральне число, більше за 1. 1150. 1) (6; 3); 2) (4; 2); 3) (1; 2); 4) (4; –3); 5) (–5; –7); 6) (1,2; –0,7). 1151. 1) (–5; 20); 2) (–1; 3); 3) (–2; –1); 4) (–3; 4). 1152. 1) (0; –6); 2) (8; 6); 3) (–5; –4); 4) (4; –3). 1153. 1) (1; –1); 2) (–2; 0,5); 3) (14; 2). 1155. 1) 14; 2) 0,25. 1156. 7 левів. 1158. 24n – 1 = (24)n – 1 = 16n – 1. Останньою цифрою степеня 16n є 6. Тоді останньою цифрою даного виразу є 5.
1168. 1) (8; 1); 2) (1,2; 0); 3) (–1; –2); 4) (7; –1); 5) (4; –1); 6) (6; –2); 7) (2; –2); 8) (5; 6). 1169. 1) (1; 2); 2) (3; –1); 3) (4; 2); 4) (6; 5); 5) (1,5; 0,5); 6) (1; –1). 1170. 1) (–3; –4); 2) (1; –0,5); 3) 5![]() ;
; ![]() ; 4) (2; –2). 1171. 1) (–0,6; –3,2); 2) (1; 3). 1172. 1) (1; 1); 2) (–3; 3). 1173. 1) (–20; –0,5); 2) (–2; 3). 1174. 1)
; 4) (2; –2). 1171. 1) (–0,6; –3,2); 2) (1; 3). 1172. 1) (1; 1); 2) (–3; 3). 1173. 1) (–20; –0,5); 2) (–2; 3). 1174. 1) ![]() ; 2
; 2![]() ; 2) (–10; 5).
; 2) (–10; 5).
1175. 1) (–5; –6); 2) (1; –6). 1176. a = 5,6, b = 0,8. 1177. m = 9, n = –12. 1178. 1) y = –0,2x + 1,4; 2) y = –x + 1. 1179. 1) y = –0,5x + + 3,5; 2) y = 3x + 3. 1181. 1) (3; –1,6); 2) розв’язків немає.
1184. –0,8. 1185. 2. 1186. 1) (3; –3); 2) (1,5; 0,75); 3) 4; ![]() ; 4) (–5; 6); 5) (–2,4; –4). 1187. 1) (10; 5); 2) (0,5; 1,5); 3) (–8; –28). 1188. 1) (0,2; 1); 2) (1; –1). 1189. 1)
; 4) (–5; 6); 5) (–2,4; –4). 1187. 1) (10; 5); 2) (0,5; 1,5); 3) (–8; –28). 1188. 1) (0,2; 1); 2) (1; –1). 1189. 1) ![]() ;
; ![]() ; 2) (2; –2). 1191. 14 коробок. 1192. 1) 6; 2) –2,5. 1193. 9 задач. 1194. 2 год. 1196. 96 дерев. 1201. 63 аршини синього сукна та 75 аршинів чорного. 1202. 7 чотиримісних човнів і 3 шестимісних. 1203. 9 кг, 7 кг. 1204. 8 га, 6 га. 1205. 9 деталей, 6 деталей. 1206. 4 ц, 5 ц. 1207. 14 грн, 12 грн. 1208. 3 грн, 2 грн. 1209. 58 км/год, 70 км/год. 1210. 60 км/год, 40 км/год. 1211. 4 км/год, 16 км/год. 1212. 84 км/год, 79 км/год. 1213. 80 л, 60 л. 1214. 28 пасажирів, 36 пасажирів. 1215. 18 км/год, 2 км/год. 1216. 25 км/год, 2,5 км/год. 1217. 5 мішків, 7 мішків. 1218. 40 рупій, 170 рупій. 1219. 42 роки, 15 років. 1220. 60 років, 12 років. 1221. 45 костюмів, 30 костюмів. 1222. 18 грн, 42 грн. 1223. 3 грн, 4 грн. 1224. 20 грн, 8 грн. 1225. 800 грн, 600 грн. 1226. 900 грн, 300 грн. 1227. a = 120, b = 100. 1228. 12; 15. 1229. 100 кг, 200 кг. 1230. 20 кг, 30 кг. 1231. 87. 1232. 6 см, 8 см. 1233. 5 см, 7 см. 1234. 3 км/год, 12 км/год. 1235. 5 км/год, 4 км/год. 1236. 12 км/год. 1237. 60 т. 1238. 50 км/год, 75 км/год, 90 км/год, 450 км. 1239. 48 км/год, 60 км/год. 1240. 48 км/год, 16 км/год. 1241. 320 г, 480 г. 1242. 63 кг, 15 кг. 1243. 72. 1244. 39. 1245. 24 л, 40 л. 1246. 28 л, 42 л. 1247. 1) Такого числа не існує; 2) будь-яке двоцифрове число, у якого цифра десятків на 2 більша за цифру одиниць, на 18 більше за число, записане тими самими цифрами, але у зворотному порядку. 1248. 8 косарів. 1256. 2) (b3 – 2b2 + 3)× × (b3 + 2b2 – 3); 4) (3x – 7) (3x + 5). 1257. a2 = c + 2b. 1258. 7,5. 1260. 8. 1277. Не існують. Вказівка. Знайдіть суму даних многочленів. 1279. 1) 1
; 2) (2; –2). 1191. 14 коробок. 1192. 1) 6; 2) –2,5. 1193. 9 задач. 1194. 2 год. 1196. 96 дерев. 1201. 63 аршини синього сукна та 75 аршинів чорного. 1202. 7 чотиримісних човнів і 3 шестимісних. 1203. 9 кг, 7 кг. 1204. 8 га, 6 га. 1205. 9 деталей, 6 деталей. 1206. 4 ц, 5 ц. 1207. 14 грн, 12 грн. 1208. 3 грн, 2 грн. 1209. 58 км/год, 70 км/год. 1210. 60 км/год, 40 км/год. 1211. 4 км/год, 16 км/год. 1212. 84 км/год, 79 км/год. 1213. 80 л, 60 л. 1214. 28 пасажирів, 36 пасажирів. 1215. 18 км/год, 2 км/год. 1216. 25 км/год, 2,5 км/год. 1217. 5 мішків, 7 мішків. 1218. 40 рупій, 170 рупій. 1219. 42 роки, 15 років. 1220. 60 років, 12 років. 1221. 45 костюмів, 30 костюмів. 1222. 18 грн, 42 грн. 1223. 3 грн, 4 грн. 1224. 20 грн, 8 грн. 1225. 800 грн, 600 грн. 1226. 900 грн, 300 грн. 1227. a = 120, b = 100. 1228. 12; 15. 1229. 100 кг, 200 кг. 1230. 20 кг, 30 кг. 1231. 87. 1232. 6 см, 8 см. 1233. 5 см, 7 см. 1234. 3 км/год, 12 км/год. 1235. 5 км/год, 4 км/год. 1236. 12 км/год. 1237. 60 т. 1238. 50 км/год, 75 км/год, 90 км/год, 450 км. 1239. 48 км/год, 60 км/год. 1240. 48 км/год, 16 км/год. 1241. 320 г, 480 г. 1242. 63 кг, 15 кг. 1243. 72. 1244. 39. 1245. 24 л, 40 л. 1246. 28 л, 42 л. 1247. 1) Такого числа не існує; 2) будь-яке двоцифрове число, у якого цифра десятків на 2 більша за цифру одиниць, на 18 більше за число, записане тими самими цифрами, але у зворотному порядку. 1248. 8 косарів. 1256. 2) (b3 – 2b2 + 3)× × (b3 + 2b2 – 3); 4) (3x – 7) (3x + 5). 1257. a2 = c + 2b. 1258. 7,5. 1260. 8. 1277. Не існують. Вказівка. Знайдіть суму даних многочленів. 1279. 1) 1![]() ; 2)
; 2) ![]() ; 3) –0,2; 4) 5; 5) 3; 6)
; 3) –0,2; 4) 5; 5) 3; 6) ![]() . 1280. 1) –0,4;
. 1280. 1) –0,4;
2) 4; 3) розв’язків немає; 4) коренем рівняння є будь-яке число. 1282. 3. 1283. –4. 1285. 1) 20; 2) 5,93. 1286. 1) 2,7; 2) 0,4; 3) 23; 4) 51,2. 1289. –4. 1290. ![]() . 1292. 1) 16. Вказівка. Подайте другий доданок у вигляді суми двох доданків: 1 66 4 68, æ , =1 66 2 34 2, æ , æ =
. 1292. 1) 16. Вказівка. Подайте другий доданок у вигляді суми двох доданків: 1 66 4 68, æ , =1 66 2 34 2, æ , æ =
1 66 2 34, æ , 1 66 2 34, æ , ; 2) 0,16. 1293. При a = c або b = d. 1296. 1) 0,5; 2) 0. 1299. 1) 1; 2) 4. 1309. 1) 2; 2) 0,5; 3) −![]() . 1315. 1) −
. 1315. 1) −![]() ; 2)
; 2) ![]() .
.
1321. 1) 9; 2) 0,064; 3) 1. 1327. Вказівка. n (n + 2) (n + 4) (n + 6) + 16 =
= (n2 + 6n) (n2 + 6n + 8) + 16 = (n2 + 6n + 4 – 4) (n2 + 6n + 4 + 4) + 16 =
(n 2 6n 4)2 42 16 (n 2 6n 4) .2 1328. Вказівка. Нехай n — дане натуральне число. Треба розглянути два випадки: n = 3k + 1 або n = 3k + 2, де k — ціле невід’ємне число. 1329. Вказівка. Розгляньте чотири можливих випадки: 1) n = 5k + 1; 2) n = 5k + 2; 3) n = = 5k + 3; 4) n = 5k + 4, де k — ціле невід’ємне число. 1330. Можна. Вказівка. Розгляньте випадки, коли n = 3k, n = 3k + 1 і n = 3k + 2, де k — ціле невід’ємне число. 1338. −![]() . 1345. 1) (–2; 1); 2) (3; –2);
. 1345. 1) (–2; 1); 2) (3; –2);
3) (1; –1); 4) (4; 2). 1346. 2. 1347. –1. 1348. 32 учні та учениці. 1349. 15 м/с, 10 м/с. 1350. 64 %. 1351. 120 г, 60 г. 1352. 8 л, 2 л. 1353. 30 га, 40 га. 1354. 20 га, 25 га. 1355. 12 кг. 1356. 29. 1357. 91. Вказівка. Якщо дане число дорівнює x, то отримане число дорівнює 10x + 1000 + 1 = 10x + 1001 або 21x. 1358. 16; 12.
Відповіді до завдань «Перевірте себе» в тестовій формі
ВІДПОВІДІ ДО ЗАВДАНЬ «ПЕРЕВІРТЕ СЕБЕ» В ТЕСТОВІЙ ФОРМІ
|
Номер |
Номер задачі |
|||||||||||
|
завдання |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
1 |
В |
А |
Б |
В |
В |
А |
Б |
В |
Б |
В |
Б |
Г |
|
2 |
Г |
В |
Г |
Г |
В |
В |
Б |
В |
Б |
А |
Г |
А |
|
3 |
Г |
Г |
А |
Б |
Б |
В |
А |
Б |
В |
А |
А |
В |
|
4 |
В |
Б |
В |
В |
В |
Б |
Б |
Г |
В |
Б |
А |
Г |
|
5 |
В |
Г |
Г |
Б |
Б |
Б |
А |
В |
А |
В |
Г |
Б |
|
6 |
А |
Г |
Б |
Б |
В |
Б |
А |
А |
В |
В |
Б |
А |
|
7 |
В |
Г |
А |
Б |
В |
Г |
А |
Б |
В |
А |
Б |
Б |
ПРЕДМЕТНИЙ ПОКАЖЧИК
Аргумент 153
Винесення спільного множника 88
Вираз алгебраїчний 5
— зі змінними 5
— цілий 6
— числовий 5
Віднімання многочленів 66
Властивості рівнянь 199
— степеня 45–47
Графік лінійного рівняння з двома змінними 206
— лінійної функції 182
— прямої пропорційності 184
— рівняння з двома змінними 200
— функції 170
Двочлен 61
Добуток різниці та суми двох виразів 101 — степенів 45
Додавання многочленів 66
Зведення подібних членів 62
Змінна 5
— залежна 151
— незалежна 151
Значення виразу 5
— — зі змінною 5
— — числового 5
— функції 154
Квадрат різниці двох виразів 112
— неповний різниці двох виразів 130
— неповний суми двох виразів 131
— суми двох виразів 112
— числа 37
Коефіцієнт одночлена 54
Корінь рівняння 14, 198
Куб числа 37
Метод групування 95
— додавання 227
— підстановки 223
Многочлен 61
Множення многочлена на многочлен 81
Область визначення функції 153
Одночлен 53
— стандартного вигляду 54
Означення 13
Основа степеня 37
Основна властивість степеня 46
Піднесення до степеня 37
— — — добутку 47
— — — степеня 47 Подібні члени 62
Показник степеня 37
Рівняння з двома змінними 198
— лінійне з двома змінними 205
— — — однією змінною 13
Різниця квадратів 106
— кубів 131
— многочленів 66
Розв’язок рівняння 14
— — з двома змінними 198
— системи рівнянь 215
Розкладання на множники многочлена 87
— — — різниці квадратів 106
— — — різниці кубів 131
— — — суми кубів 131
Стандартний вигляд одночлена 54
Степінь 37
— одночлена 55
— многочлена 62
— числа 37
Тотожність 32
Тотожно рівні вирази 32
Тричлен 61
Формула квадрата різниці 112
— — суми 112
— різниці квадратів 106
— — кубів 131
— скороченого множення 101
— суми кубів 130
Функція 153
— лінійна 183
— пряма пропорційність 183
Член многочлена 61
![]()
ЗМІСТ
Від авторів .........................................................................3
Умовні позначення ..............................................................4
![]() 1. Вступ до алгебри .......................................................5 l Книга про відновлення та протиставлення ............ 11
1. Вступ до алгебри .......................................................5 l Книга про відновлення та протиставлення ............ 11
§ 1. Лінійне рівняння з однією змінною .................................. 13
2. Лінійне рівняння з однією змінною ........................... 13 3. Розв’язування текстових задач ..................................20
Завдання № 1 «Перевірте себе» в тестовій формі .............. 29
Головне в параграфі 1 ........................................................ 30
§ 2. Цілі вирази .................................................................. 31
4. Тотожно рівні вирази. Тотожності ............................. 31
5. Степінь з натуральним показником ........................... 37
6. Властивості степеня з натуральним показником ..........45
7. Одночлени .............................................................. 53
8. Многочлени ............................................................ 61 9. Додавання і віднімання многочленів .......................... 66
Завдання № 2 «Перевірте себе» в тестовій формі .............. 73
10. Множення одночлена на многочлен ..........................74 11. Множення многочлена на многочлен.........................81
12. Розкладання многочлена на множники.
Винесення спільного множника за дужки ................87 13. Розкладання многочлена на множники.
Метод групування ................................................. 95
Завдання № 3 «Перевірте себе» в тестовій формі .............100
14. Добуток різниці та суми двох виразів .....................101
15. Різниця квадратів двох виразів ..............................106
16. Квадрат суми та квадрат різниці двох виразів .........112
l ![]() Трикутник Паскаля ...........................................121
Трикутник Паскаля ...........................................121
17. Перетворення многочлена у квадрат суми
або різниці двох виразів .......................................122
Завдання № 4 «Перевірте себе» в тестовій формі .............129
18. Сума й різниця кубів двох виразів ..........................130
19. Застосування різних способів розкладання многочлена на множники ...................137
зміст
Завдання № 5 «Перевірте себе» в тестовій формі .............145
l![]() Мова, зрозуміла всім .........................................146
Мова, зрозуміла всім .........................................146
Головне в параграфі 2 .......................................................149
§ 3. Функції ......................................................................151
20. Зв’язки між величинами. Функція .........................151
21. Способи задання функції .......................................163
22. Графік функції .....................................................170 23. Лінійна функція, її графік і властивості .................181
Завдання № 6 «Перевірте себе» в тестовій формі .............194
Головне в параграфі 3 .......................................................196
§ 4. Системи лінійних рівнянь із двома змінними .....................197
24. Рівняння з двома змінними ...................................197
25. Лінійне рівняння з двома змінними та його графік .....205
![]() l Як будували міст між геометрією та алгеброю .....214
l Як будували міст між геометрією та алгеброю .....214
26. Системи рівнянь із двома змінними. Графічний метод розв’язування системи
двох лінійних рівнянь із двома змінними ...............215
27. Розв’язування систем лінійних рівнянь
методом підстановки .............................................222
28. Розв’язування систем лінійних рівнянь
методом додавання ...............................................226
29. Розв’язування задач за допомогою систем лінійних рівнянь ...................234 Завдання № 7 «Перевірте себе» в тестовій формі .............244
Головне в параграфі 4 .......................................................246
Вправи для повторення курсу алгебри 7 класу .....................248
Дружимо з комп’ютером ...................................................258
Проєктна робота ...............................................................264
Відомості з курсу математики 5–6 класів ............................266
Відповіді та вказівки до вправ ..........................................276
Відповіді до завдань «Перевірте себе» в тестовій формі .....284
Предметний покажчик .....................................................285
Âèäàíî çà ðàõóíîê äåðæàâíèõ êîøò³â.
Ïðîäàæ çàáîðîíåíî
Íàâ÷àëüíå âèäàííÿ
ÌÅÐÇËßÊ Àðêàä³é Ãðèãîðîâè÷
ÏÎËÎÍÑÜÊÈÉ Â³òàë³é Áîðèñîâè÷ ßʲРÌèõàéëî Ñåìåíîâè÷
ÀËÃÅÁÐÀ
ϳäðó÷íèê äëÿ 7 êëàñó çàêëàä³â çàãàëüíî¿ ñåðåäíüî¿ îñâ³òè
2-ãå âèäàííÿ, ïåðåðîáëåíå
Ðåêîìåíäîâàíî
̳í³ñòåðñòâîì îñâ³òè ³ íàóêè Óêðà¿íè
Ãîëîâíèé ðåäàêòîð Ã. Ô. Âèñîöüêà
³äïîâ³äàëüíèé çà âèïóñê Ì. Â. Ìîñêàëåíêî
˳òåðàòóðíèé ðåäàêòîð Ò. ª. Öåíòà
Õóäîæíº îôîðìëåííÿ òà äèçàéí Ä. Â. Âèñîöüêîãî
Òåõí³÷íèé ðåäàêòîð Î. Â. Ãóëüêåâè÷ Êîðåêòîð Ò. ª. Öåíòà
Êîìï’þòåðíå âåðñòàííÿ C. ². Ñåâåðèí
Ôîðìàò 60×90/16. Ïàï³ð îôñåòíèé. Ãàðí³òóðà øê³ëüíà.
Äðóê îôñåòíèé. Óì. äðóê. àðê. 18,00. Îáë.-âèä. àðê. 16,42.
Òèðàæ 99 566 ïðèì. Çàìîâëåííÿ ¹ 21
ÒΠÒÎ «Ã³ìíàç³ÿ»,
âóë. Âîñüìîãî Áåðåçíÿ, 31, ì. Õàðê³â 61052
Òåë.: (057) 719-17-26, (057) 719-46-80, ôàêñ: (057) 758-83-93
E-mail: contàct@gymnasia.com.ua www.gymnasia.com.ua
Ñâ³äîöòâî ñóá’ºêòà âèäàâíè÷î¿ ñïðàâè ÄÊ ¹ 644 â³ä 25.10.2001
Íàäðóêîâàíî ç ä³àïîçèòèâ³â, âèãîòîâëåíèõ ÒΠÒÎ «Ã³ìíàç³ÿ», ó äðóêàðí³ ÏÏ «Ìîäåì»,
âóë. Âîñüìîãî Áåðåçíÿ, 31, ì. Õàðê³â 61052
Òåë. (057) 758-15-80
Ñâ³äîöòâî ñóá’ºêòà âèäàâíè÷î¿ ñïðàâè ÕÊ ¹ 91 â³ä 25.12.2003
[1] Цельсій Андерс (1701–1744) — шведський астроном і фізик. У 1742 р. розробив температурну шкалу, названу на його честь.
[2] Фаренгейт Габріель Даніель (1686–1736) — німецький фізик.
У 1724 р. розробив температурну шкалу, названу на його честь.
[3] Демохар (IV–III ст. до н. е.) — давньогрецький політик, оратор та історик.
[4] Лагранж Жозеф Луї (1736–1813) — французький математик і механік.
[5] Ми розповідали про нього на с. 11, 12.
[6] Дирхем — старовинна арабська срібна монета.
[7] У наведеній таблиці значення аргументу в кожному наступному стовпці на 1 більше за значення аргументу в попередньому стовпці. У такому випадку говорять, що таблицю складено з кроком 1.
[8] Войтяховський Юхим Дмитрович (1750–1812) — російський математик-педагог. Його «Теоретичний і практичний курс чистої математики» (1787–1790) витримав багато видань і протягом 40 років був одним із найпоширеніших посібників для шкіл того часу.
[9] Для даної функції існує спеціальне позначення y = [x] (читають: «y дорівнює цілій частині числа x»).
[10] Бхаскара ІІ (1114–1185) — індійський математик і астроном, автор трактату «Вінець системи» (бл. 1150 р.), у якому викладено методи розв’язування ряду алгебраїчних задач.
[11] Дану функцію називають дробовою частиною числа, і для неї існує спеціальне позначення: y = {x}. За означенням {x} = x – [x], де [x] — ціла частина x. Наприклад, {3,2} = 0,2; {–3,2} = 0,8; {–0,16} = 0,84; {2} = 0.
[12] Якщо змінні в рівнянні позначено буквами, відмінними від x і y, то, записуючи розв’язок у вигляді пари, потрібно домовитися, значення якої змінної треба ставити на перше місце в парі, а якої — на друге. Зазвичай беруть до уваги порядок букв латинського алфавіту.
[13] Лев — грошова одиниця Болгарії.
[14] А. П. Чехов (1860–1904) — видатний російський письменник.
[15] Аршин — старовинна міра довжини, що дорівнює 71,12 см.
[16] Л. М. Толстой (1828–1910) — видатний російський письменник.


про публікацію авторської розробки
Додати розробку


 B
B