Конспект уроку "Числові вирази. Буквені вирази та формули"
Урок на тему: «Числові вирази. Буквені вирази та формули»
Тема. Числові вирази. Буквені вирази та формули
Мета: сформувати уявлення учнів про поняття «числові вирази» та «буквені вирази»; навчити розпізнавати числові і буквені вирази, читати їх; виробити вміння знаходити значення виразів за умови різних значень змінної; виховувати математичну цікавість до відомих математиків та їх формул.
Тип уроку: засвоєння нових знань.
Хід уроку
І. Актуалізація опорних знань
Усні вправи
- Обчисліть: 1) 12 + 16; 2) 39 – 24; 3) 18 · 2; 4) 39 : 3; 5) 75 + (25 + 13);
6) ![]() ; 7) (20 : 5) – 4; 8) 125000 : 1000.
; 7) (20 : 5) – 4; 8) 125000 : 1000.
2. У першому ящику було 16 кг апельсин, що на 3 кг менше, ніж у третьому, а у другому на 2 кг більше, ніж у першому. Скільки апельсин було в трьох ящиках?
II. Формування нових знань
- Поняття числового виразу
Розглянувши розв'язання задач в п. 2 , усних вправ, учитель наголошує, що для розв'язання цієї задачі можна було скласти один запис:
( 16 – 3 ) + ( 16 + 2 ) + 16 = 45.
Такий запис, що складається з чисел, знаків дій та дужок називається числовим виразом.
Приклади числових виразів див. у № 1 до усних вправ.
Якщо в числовому виразі виконати всі дії (в тому порядку, який відомий учням з початкової школи), то отримане число називається значенням числового виразу.
Приклад. Значенням виразу ( 16 – 3 ) + ( 16 + 2 ) + 16 є число 45 кг.
- Читання числових виразів
Уже з п'ятого класу слід привчати учнів читати вирази, використовуючи назви дій. Тому після введення поняття числового і буквеного виразу, тому вчитель повинен звертати увагу учнів на те, що вирази, які містять знаки арифметичних дій, можна читати, використовуючи назви цих дій.
Приклад
Сума 9 і а : 9 + а;
різниця 13 і в : 13 – в;
добуток 10 і суми 13 і х : 10 · (13 + х);
частка від ділення різниці 17 і 3 на а : (17 – 3) : а.
- Поняття буквеного виразу
Після введення поняття числового виразу та його значення учням запропонувати розглянути розв’язання задач у підручнику ( ст.. 54 – 55).
Питання до класу
- Чим схожі способи розв’язання задач з підручника із задачею з усної вправи?
- Що спільного будуть мати вирази для розв'язання 1) і 2)? А чим будуть відрізнятися ці записи?
Приклад 2. (Записати на дошці)
Знайти значення виразу: 475 + х, якщо х = 208.
Розв'язання. Якщо х = 208, то 475 + х = 475 + 208 = 683.
Отже:
- числовими виразами називається ...;
- значення числового виразу називається...;
- буквеним виразом називається ...
4. Розглядаємо поняття формули за підручником ( ст. 55 – 56).
III. Закріплення знань, засвоєння вмінь
Усні вправи
- Назви числові, буквені вирази і формули серед таких виразів (ст.. 56 № 336).
- Назвіть доданки в сумі:
1) (18 – 7) + 14; 2) (х – 75) + 16; 3) (а – 13) + (b – 86).
3. Складіть вираз до задачі № 337.
Вправи для письмового виконання
№ 339. Чим задача схожа до задачі № 337.
№ 340 і № 341. Завдання на закріплення правил читання буквених виразів і відпрацювання навичок знаходження їх значень.
№ 343. Повторюються властивості додавання і віднімання натуральних чисел (для спрощення буквених виразів) та відпрацьовуються обчислювальні навички. За відомими значення змінних обчислити вирази та заповнити таблицю значень.
IV. Підсумок уроку
Щоб зацікавити учнів до вивчення математики та відомих вчених, пропоную за відомою формулою вченого-математика (фізиків) знайти про нього інформацію в книгах чи Інтернеті, та скласти невелику розповідь про нього та його здобутки на наступний урок.
1. ![]() ; (формула Герона)
; (формула Герона)
2. ![]() ; (теорема Піфагора)
; (теорема Піфагора)
3. ![]() ; (закон Архімеда)
; (закон Архімеда)
4. ![]() ; (закон Паскаля)
; (закон Паскаля)
5. ![]() (формула Ньютона-Лейбніца)
(формула Ньютона-Лейбніца)
6. ![]() ; (формула Ейлера)
; (формула Ейлера)
7. ![]() (формула Колмагорова)
(формула Колмагорова)
8. ![]() ; (закон Бернуллі (закон збереження енергії))
; (закон Бернуллі (закон збереження енергії))
9. 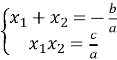 (теорема Вієта)
(теорема Вієта)
10. ![]() . (теорема відносності Ейнштейна)
. (теорема відносності Ейнштейна)
V. Домашнє завдання
1. Прочитати & 10 ( ст. 54 – 56); вивчити означення.
2. Виконати вправи: № 338; 342; 345.
3. Підготувати доповідь про вченого.
Додатки до уроку
………………………………………………………………………………………

……………………………………………………………………………………………….

……………………………………………………………………………………..
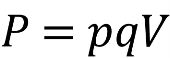
………………………………………………………………………………………..

…………………………………………………………………………………..
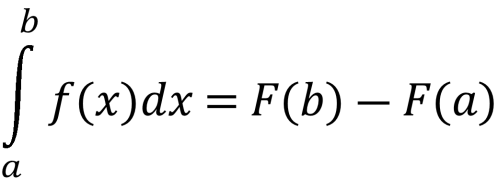
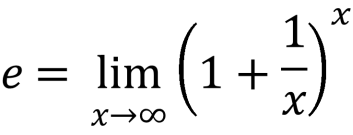
………………………………………….……………………………………
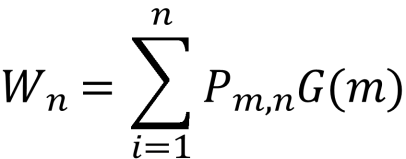
………………………………………………………………………………..
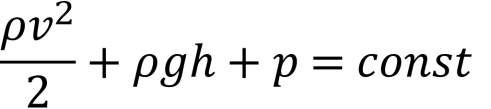
………………………………………………………………………………….
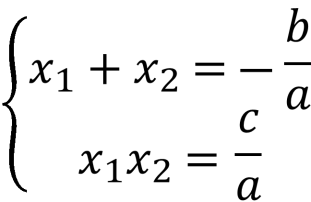
………………………………………………………………………………….
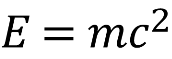
5


про публікацію авторської розробки
Додати розробку
