Конспект уроку: Властивості арифметичного квадратного кореня

Тема уроку: Властивості арифметичного квадратного кореня

Мета:

сформувати в учнів знання про властивості арифметичного квадратного кореня, сформульовані у вигляді теорем; формувати вміння застосовувати вивчені властивості для обчислення значень виразів, спрощення та перетворення виразів; формувати культуру усних та письмових обчислень;

формувати вміння відбирати й застосовувати потрібні знання та способи діяльності для досягнення цієї мети; знаходити зв’язок з раніше вивченим: переносити набуті знання в нові ситуації;

сприяти умінню висловлювати власну думку, слухати і чути інших.

Тип уроку: засвоєння нових знань.

Обладнання: конспект уроку, підручник А.Г. Мерзляк, ПК (телефон)  з інтернетом,  «Сlassroom», «Google Meet» .

Хід уроку

І. Етап орієнтації

3. Повідомлення теми, мети та завдань уроку.

На минулому уроці ми вивчили поняття арифметичного квадратного кореня. Сьогодні ми познайомимося з властивостями арифметичного квадратного кореня, навчимося використовувати їх при обчисленні виразів, що містять квадратні корені. Отже, пишемо число, класна робота та тему уроку «Властивості арифметичного квадратного кореня».

II етап. Актуалізація опорних знань.

А зараз пропоную вам невеличку розминку для нашого розуму, щоб налаштувати його на серйозну роботу.

1. Завершіть речення:

2. Подумайте, обчисліть усно:

III етап. Вивчення нової теми. Метод проблемного навчання

Зараз вам потрібно самостійно вирішити два приклади різними способами і з них вибрати оптимальний варіант рішень, обґрунтувати свій вибір

1) Обчислити:

Вибір оптимального варіанту

    1 варіант обчислення:

2 варіант обчислення:

- Який спосіб зручніше і швидше?

- Таким чином, ми з вами вивели і довели 1 властивість квадратних коренів, який називається властивість квадратного кореня з добутку

В конспект

- Для розуміння, засвоєння і закріплення даного властивості усно виконаємо наступну вправу.

Первинне закріплення. Обчисліть:

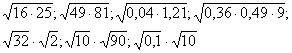
- Зверніть увагу, що ця властивість можна застосовувати як зліва направо, так і справа наліво.

2) Обчисліть

1 варіант обчислення:

2 варіант обчислення:

В конспект

Первинне закріплення. Обчисліть

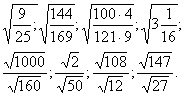
3.                   Розглянемо рівності: 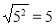, 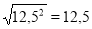. Чи згодні ви, що для будь-якого значення а виконується рівність 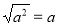? Чи правильною буде рівність 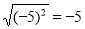. Звичайно, ця рівність є неправильною, так як 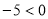. Насправді, , 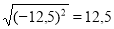. Отже, справедливою є така теорема:

Теорема 15.1. Для будь-якого дійсного числа а виконується рівність .

Доведення.

Для того щоб довести рівність , треба показати, що і .

Маємо: при будь-якому а. Також з означення модуля випливає, що Отже, теорему доведено.

Наприклад, ; .

Розглянемо приклад.

Приклад. Спростіть вираз , якщо .

Розв’язання. .

4. Наступна теорема узагальнює доведений факт.

Теорема 15.2 (арифметичний квадратний корінь зі степеня). Для будь-якого дійсного числа а та будь-якого натурального числа n виконується рівність .

Наприклад, ; .

Первинне закріплення знань.

;

;

;

.

ІV. Застосування нових знань і умінь

1. Працюємо з підручником

Параграф 15, ст 118. Розв’язати номери

2. Індивідуальна робота

 V. Домашнє завдання.

Опрацювати §15, № 474( 1, 2, 6, 7, 12), 476 (1-3), 484, 478(1-3)

IV. Підбиття підсумків уроку.

Знайдіть і виправте помилки в записі:

а) ;

б) ;

в)  ;

г)  .

Ми розглянули одну з тем математики «Арифметичний квадратний корінь», але об’єм математичних знань безкінечний, самі математичні знання неоцінені, а області застосувань математики  безмежні.

 Тож, я впевнена, що вам математика завжди буде в нагоді.