Конспект уроку з алгебри для 10 класу на тему "Арифметичний корінь п-го степеня і його властивості"

Тема: Арифметичний корінь п-го сте­пеня і його властивості.

Мета уроку:

• повторити й систематизувати знання учнів про поняття кореня  n – го степеня й арифметичного кореня n – го степеня;
• сформувати знання про властивості кореня  n – го степеня;
• формувати вміння застосовувати ці знання під час перетворення виразів;
• формувати інформаційну та полікультурну  компетентність;
• сприяти формуванню та розвитку інтелектуальних та творчих здібностей учнів;
• розвивати логічне мислення, математичну мову, пізнавальний інтерес учнів, вміння шукати цікаву інформацію;
• виховувати відповідальність, прагнення до самовдосконалення, патріотизм, любов до рідного краю.

Компетенції: Спілкування державною мовою: розуміти, пояснювати і перетворювати тексти математичних задач (усно і письмово), грамотно висловлюватися рідною мовою; доречно та коректно вживати в мовленні математичну термінологію, чітко, лаконічно та зрозуміло формулювати думку, аргументувати, доводити правильність тверджень; поповнювати свій словниковий запас.

Тип уроку:   засвоєння нових знань

Обладнання: робочий зошит, підручник, комп’ютерна презентація; інтерактивні завдання, розроблені в додатку Learning Apps

Хід уроку.

1. Організаційний етап.

Вчитель пропонує учням записати своє прізвище у чаті конференції

2. Перевірка домашнього завдання: Дякую вам за надіслане розв’язання  ДЗ на клас – рум, я переглянула і оцінюю роботи 4 – х учнів.
3. Мотивація навчальної діяльності:

Я хочу розпочати наш урок із слів поета Миколи  Дорізо: «Життя – як розв’язування задачі. З невдачі зумій ти добути корінь удачі». Отже, сьогодні ми будемо не тільки знаходити корінь n-го степеня, але й «добувати корінь удачі».

І удача  сьогодні  буде на стороні тих учнів , які використавши  свої  знання та вміння з вивченої теми отримають правильний результат.

В попередніх класах ви вивчили властивості квадратного кореня, застосовували ці властивості до перетворення виразів з коренями. Та якщо існує дія піднесення до степеня ( квадрат, куб,  четверта степінь числа ), то і існує обернена дія – добування  кореня п – го степеня . Тому на сьогоднішньому уроці ми з вами розширимо поняття кореня n–го степеня і вивчимо його властивості.

4. Актуалізація опорних знань

Вправа із додатку Learning Apps. Вчитель призначає 4 – х учнів, які виконують по одному стовпчику. Правильність виконання контролює один учень (відмінник). Які властивості квадратного кореня ви застосували при розв’язуванні цих вправ? Запишіть їх у зошиті (вчитель подає їх на слайді 2).

https://learningapps.org/view5264787  (5 хв)

5. Вивчення нового матеріалу і первинне засвоєння знань:  розглянемо основні властивості кореня n–го степеня. Якщо корінь парного степеня, то підкореневий вираз має бути невід’ємним. Якщо ж корінь непарного степеня, то підкореневий вираз може бути як додатним, так і від’ємним, або дорівнювати нулю (слайд 4). Звернемося до підручника і ознайомимося з теоремами про властивості кореня п – го степеня (с. 28), слайд 4 – 6.

• Теорема 5.1: 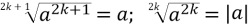– перша теорема про корінь із степеня
• Теорема 5.2: 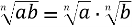– корінь із добутку
• Теорема 5.3: 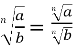– корінь із частки
• Теорема 5.4: 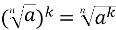– корінь степеня
• Теорема 5.5: 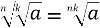– корінь із кореня
• Теорема 5.6: 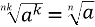– друга теорема про корінь із степеня. 

https://learningapps.org/view4146619

Необхідно визначитись, яка властивість буде застосована при спрощенні виразів.

Обговорення правильності виконання кожного завдання.

6. Підсумки уроку

Фронтальне опитування по вивченому матеріалу.

Вчитель: приємно повідомити, що протягом уроку ми створювали умови для мотивації до самостійної роботи і останнє: на цьому уроці ми лише описали, але не довели жодної властивості, тому я рекомендую розглянути доведення властивостей самостійно за підручником, а на наступному уроці ми розглянемо їх в класі

7. Домашнє завдання:

п. 5 вивчити формули

№№ 5.2, 5.4