Презентація "Аркфункції та найпростіші тригонометричні рівняння"
Про матеріал
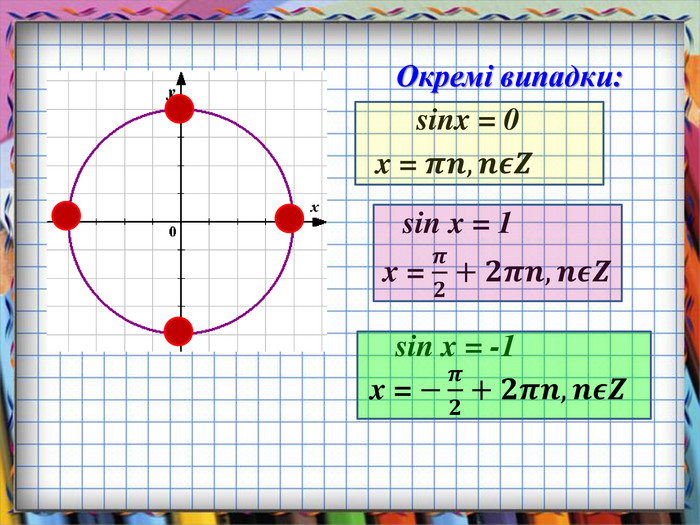
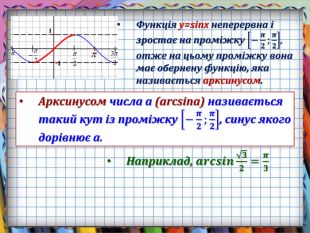
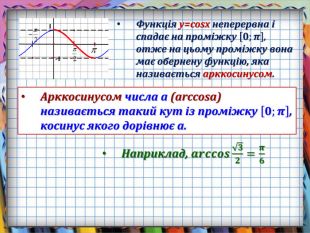
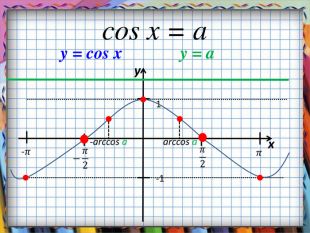
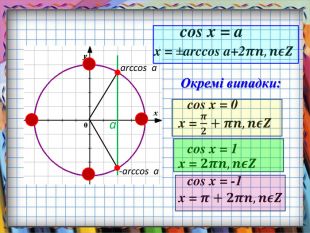
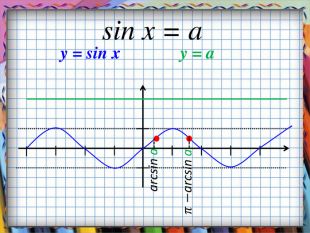
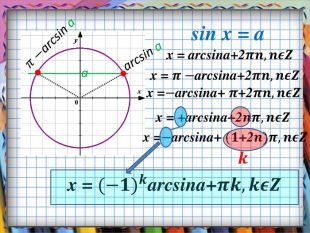
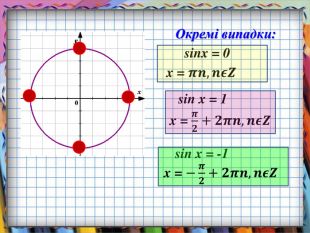
Презентація призначена для вивчення математики на рівні стандарту. Зручно використовувати, коли потрібно компактно подати необхідний теоретичний матеріал, щоб залишився час для практичних вправ. Анімація допомагає учням усвідомити формули коренів найпростіших тригонометричних рівнянь, включаючи окремі випадки. Містить також актуалізацію опорних знань. Може бути використано і з метою повторення, узагальнення та систематизації знань.
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку























-

Модягина Наталія
18.02.2023 в 15:16
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Милка Наталія Василівна
12.02.2023 в 12:48
Дякую!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Petrivska Oksana
26.01.2022 в 16:56
Дякую!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Руденко Валентина Олександрівна
16.01.2022 в 12:59
Дякую!
Загальна:
4.7
Структурованість
4.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Коваленко Валентина Олексіївна
20.11.2021 в 19:32
Презентація чудова, наглядно і доступно. Дякую.
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Василюк Оксана Миколаївна
16.11.2021 в 23:38
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Зубик Оля
11.11.2021 в 10:56
Дякую за гарну презентацію. Змістовно і наглядно. Чудова робота!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Нижборська Наталія
12.04.2021 в 21:30
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Новомлинська Дар'я Сергіївна
05.04.2021 в 12:10
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Асламова Любов Володимирівна
20.01.2021 в 23:37
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Гордієць Тамара Степанівна
17.01.2021 в 15:22
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Поплавська Оксана Гнатівна
12.01.2021 в 20:25
Чудова презентація! Спасибі!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Мисік Марина Олександрівна
12.01.2021 в 10:49
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Крутько Валентина Петрівна
09.12.2020 в 16:01
Доступно
Конкретно
Дякую
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Кучурян Діана Іванівна
19.05.2020 в 23:12
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Норкіна Олена
02.04.2020 в 15:21
Презентація дуже добра!!!!!!!!!!!! Спасибі
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Букарева Анастасія Анатоліївна
14.01.2020 в 08:47
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Теплова Оксана Анатоліївна
09.12.2018 в 16:54
Дуже доступно, стисло. Дякую!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Корчинська Ольга Василівна
06.11.2018 в 09:45
Дякую! Чудова презентація!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Загородня Вікторія Микитівна
21.03.2018 в 22:29
Дякую!
Чітко і лаконічно.
Загальна:
4.7
Структурованість
5.0
Оригінальність викладу
4.0
Відповідність темі
5.0
-

Наконечний Сергій Павлович
20.02.2018 в 20:35
Загальна:
4.3
Структурованість
4.0
Оригінальність викладу
5.0
Відповідність темі
4.0
-

Сальник Ольга Іванівна
20.02.2018 в 20:14
Загальна:
4.7
Структурованість
4.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 19 відгуків