Конспект уроку з геометрії для 11 класу рівня стандарту на тему:"Площа сфери і об'єм кулі"

Тема: Площа сфери. Об’єм кулі

Мета: Узагальнити і закріпити знання студентів про тіла

 обертання. Вивчити формули для обчислення площі сфери

 та об’єму кулі. Вчити застосовувати дані формули для

 розв’язування практичних задач.

Розвивати уяву, кмітливість, логічне мислення,

обчислювальні навички.

Виховувати наполегливість, самостійність, взаємоповагу,

 прагнення до найкращого результату.

 

Вид заняття: засвоєння нових знань

 

Обладнання: модель кулі, презентація, набори матеріалів для роботи в групах.

 

Література:

• Математика : 11 кл. : підруч. для загальноосвіт. навч. закл. : рівень стандарту / Г. П. Бевз, В. Г. Бевз. – К. : Генеза, 2011. – 320 с. : іл. – Бібліогр. : с. 294
• Роганін О.М. / Геометрія. 11 клас: Плани-конспекти уроків. – Х. : Веста : Видавництво «Ранок», 2006. – 2-ге вид., випр.. – 256 с. – (Сучасний урок математики)
• Мерзляк А.Г., Полонський В.Б., Якір М.С. / Збірник задач і завдань для тематичного оцінювання з геометрії для 11 класу. – Харків, Гімназія, 2001. – 128 с. : іл.

 

ХІД ЗАНЯТТЯ

 

І. Організація навчальної діяльності.

 

ІІ. Постановка навчальних завдань.

1. Продовжити вивчати тіла обертання.
2. Повторити раніше вивчений матеріал.
3. Вивчити нові формули і навчитися їх застосовувати до розв’язування задач.
4. Узагальнити одержані знання.

 

 

 

ІІІ. Перевірка домашнього завдання.

 

За готовими малюнками на слайді, студенти пояснюють розв’язання домашніх задач.

 

 

 

 

 

 

 

 

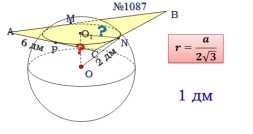
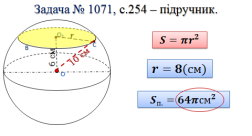
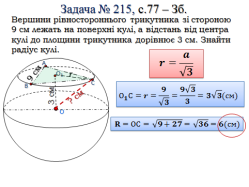
Усне бліц-опитування

 

 

 

 

 

 

 

 

 

 

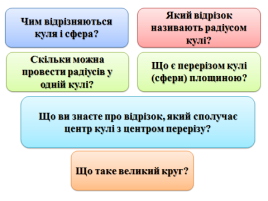
ІІІ. Вивчення нового матеріалу.

1. Актуалізація опорних знань.

- Що є у конуса, але немає в циліндра? (Вершина)

- Чого у циліндра дві, а у конуса одна? (Основа)

- Чого у циліндра безліч, а у конуса єдине? (Відрізок, що є висотою)

- Що є і у конуса, і у циліндра? (Твірні, основа – круг, бічна поверхня)

- Які основні формули ми вивчали для цих тіл обертання? (Площа бічної і повної поверхні, об’єм)

- Як ви думаєте, для кулі і сфери теж є такі формули?

- Отже, ми сьогодні з вами вивчимо формули для обчислення площі сфери і об’єму кулі.

2. Пояснення.

- Давайте пригадаємо що ми вже з вами знаємо про об’єм. Знаємо, що він вимірюється в кубічних одиницях. Для призми, наприклад, обчислити об’єм – це порахувати скільки кубиків зі стороною в одиницю вимірювання довжини поміститься всередині призми. Ми з вами це розглядали на прямокутному паралелепіпеді і з’ясували, що безпосередньо рахувати всі кубики не потрібно, а щоб дізнатися скільки їх, треба площу основи помножити на висоту. Узагальнили це правило для довільної призми.

Для піраміди, ви вже знаєте, що її об’єм становить третину об’єму призми з такою ж основою і висотою. Аналогічна ситуація з циліндром і конусом.

Виявляється, що подібне співвідношення існує і для кулі. Ви вже знаєте, що діаметральна площина ділить кулю на дві рівних частини – півкулі. Так от об’єм однієї півкулі вдвічі більший, ніж об’єм конуса з висотою і радіусом основи, що дорівнюють R, тобто радіусу півкулі і кулі. Об’єм такого конуса становитиме  . А скільки таких частинок буде в півкулі? (2) А в цілій кулі? (4). Отже, маємо формулу об’єму кулі   .

Тепер розглянемо сферу. Сфера – це поверхня кулі, її межа. Найбільший за площею переріз кулі – великий круг. Як визначити його площу? ( ). А площа сфери у 4 рази більша за площу великого круга: . Отже, запишіть у конспекти:

 

 

 

 

 

3. Первинне закріплення.

А тепер потренуємося застосовувати вивчені формули до розв’язування задач. Спочатку усно.

 

 

 

 

ІV. Розвиток математичних знань.

1. Математичний диктант.

- А зараз вам потрібно напівусно, тобто тільки з допомогою чернетки для деяких обчислень, виконати завдання і записати в зошити тільки відповідь. Завдань буде 6. Тому розмістіть їх у два стовпчики.

 

 

 

 

2. Робота в групах.

- Поділ на групи.

- Як ви думаєте, це всі тіла обертання, які існують?

- Навіть обертаючи той самий трикутник, але по-іншому, може утворитися інше тіло обертання.

- А тепер вам треба розв’язати таку задачу:

 

 

• Подумайте, уявіть яке тіло утвориться. Обговоріть в групі. Побудуйте малюнок, нанесіть на нього дані умови задачі і виконайте обчислення. По закінченню роботи представник із групи виходить до дошки продемонструвати результат, тому записи і малюнки робіть компактними, але максимально великими.
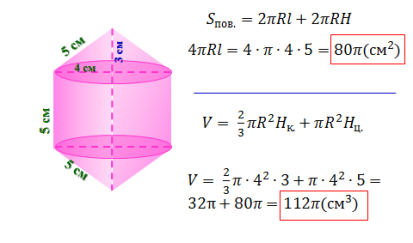• Звіримо результати:

 

 

 

 

 

 

 

V. Підсумок заняття.