КУРСОВИЙ ПРОЕКТ З навчальної дисципліни ФІЗКОЛОЇДНА ХІМІЯ ПЕРШИЙ ТА ДРУГИЙ ЗАКОНИ ТЕРМОДИНАМІКИ

                      Міністерство освіти і науки України

 Житомирський державний  університет ім. Івана Франка

                                                Кафедра хімії

 

 

 

КУРСОВИЙ ПРОЕКТ

 З навчальної дисципліни

ФІЗКОЛОЇДНА  ХІМІЯ

 

 

 

ПЕРШИЙ ТА ДРУГИЙ ЗАКОНИ ТЕРМОДИНАМІКИ

 

 

 

 

Студентки  V курсу 51 групи

напряму підготовки  Біологія^*

 

Нейкалюк Ганни Олександрівни

 

Керівник :

Гвоздієвський Є.Є.

 

Національна шкала ________________

Кількість балів: __________Оцінка: ECTS _____

Члени комісії ________________ ___________________________

(підпис) (прізвище та ініціали)

________________ ___________________________

(підпис) (прізвище та ініціали)

________________ ___________________________

(підпис) (прізвище та ініціали

 

 

 

                                    Житомир 2015

Зміст

 

 

Вступ………………………………………………………………….. 3

Розділ 1. Перший закон термодинаміки 

1.1 Формулювання першого закону термодинаміки……………..  5

1.2 Приклади розв’язання задач……   ……………………………  6

1.3 Задачі для розв’язування ………………………………………. 7

Розділ 2. Другий закон термодинаміки

1.2 Формулювання другого закону термодинаміки………………. 9

2.2 Приклади розв’язування задач…………………………………..10

2.3 Задачі для розв’язування ……………………………………….. 13

 

 

 

 

 

Вступ

 

Актуальність питання

 

Фізична  хімія – наука вивчає загальні закономірності  фізичних процесів тає теоретичною основою  всієї хімічної науки і технології хімічного виробництва. Важливим розділом фізхімії є хімічна термодинаміка. Термодинаміка – це наука про закони , перетворення енергії із одного виду в інший. Існування живого організму і всі процеси життєдіяльності в ньому нерозривно зв’язані з перетворенням  енергії , зі зміною енергетичного балансу в системі організм – оточуюче середовище. Живі системи поглинають енергію у різних формах , використовують її в метаболічних процесах , які забезпечують ріст , розвиток , розмноження.

     Відомо , що перебіг багатьох захворювань і дія на організм лікарських препаратів супроводжується зміною енергетичного метаболізму і температури тіла.

     Термодинаміка не дає відповіді на питання , яка природа чи механізм того чи іншого явища. Вона досліджує виключно енергетичну сторону процесів і здатна відповісти на питання , чи можливе протікання даного процесу з точки зору енергетики.

     Термодинаміка базується на першому і другому законах термодинаміки.

В цій курсовій роботі я розглянула та показала приклади розв’язку задач з  хімічної термодинаміки. Ці задачі мають комплексний характер та дозволять учням підготуватись до конкурсних олімпіад з хімії.

Розв’язок задач дає можливість застосувати теоретичні знання на практиці , розширити , поглибити та систематизувати  їх , стимулюють мислення учнів  розвивають послідовність в діях , логічне мислення.

 

 

 

Мета:

 розглянути основні положення першого та другого закону термодинаміки, підібрати відповідні завдання з хімічної термодинаміки , розробити методику їх розв’язку з урахуванням між предметних зв’язків з математикою та фізикою.

Завдання:

• З’ясувати основні теоретичні моменти першого та другого законів термодинаміки;
• Розглянути та розробити методику розв’язування задач , які розглядають закони термодинаміки;
• Навести умови задач для розв’язку задач, необхідних для кращого засвоєння першого та другого законів термодинаміки.

Об’єкт дослідження:

• Перший та другий закони термодинаміки.

Предмет дослідження :

• Методика розв’язування задач з даної теми.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Розділ1. Перший закон термодинаміки.

1.1 Формулювання першого закону термодинаміки

 

Пе́рший зако́н термодина́міки — одне з основних положень термодинаміки , є , по суті, законом збереження енергії у застосуванні до термодинамічних процесів. Перший закон термодинаміки сформульований в середині 19 століття в результаті робіт Саді Карно, Юліуса фон Маєра , Джеймса Прескотта Джоуля і Германа фон Гельмгольца. Перший початок термодинаміки часто формулюють як неможливість існування вічного двигуна 1-го роду ,  який здійснював би роботу , не черпаючи енергію з якого-небудь джерела.

Перший закон термодинаміки

Зміна внутрішньої енергії закритої системи , яка відбувається в рівноважному процесі переходу системи із стану 1 в стан 2 , дорівнює сумі роботи , зробленої над системою зовнішніми силами , і кількості теплоти , наданої системі: ΔU = A' + Q. Робота здійснена системою над зовнішніми тілами в процесі 1->2 (Назвемо її просто А) A=-A' , тоді закон приймає вигляд:

Q= ΔU+A

 

Кількість теплоти , що надається системі , витрачається на зміну внутрішньої енергії системи і на здійснення системою роботи проти зовнішніх сил.

 

Для елементарної кількості теплоти δQ; елементарної роботи δA і малої зміни dU внутрішньої енергії перший закон термодинаміки має вигляд:

 

δQ= δU+δA

[4,5,6]

 

1.2 Приклади розв’язування задач.

1-1

Газ разширюючись від10 до 16 л. при постійному тиску101,310³ н/м², поглинає 126 Дж теплоти. Визначити зміну внутрішньої енергії газу.

Розв’язування :

p₁ = p₂ = 101,310³ Па, V₁ = 10 л = 1*10^-2 м³ ,

V₂ =16 л = 1610^-3 м³,

Q_{p =} 126 Дж.

Згідно першого закону термодинаміки

U = Q_p – W.

Работа, зроблена газом при ізобарному розширенні може розраховуватись за таким рівнянням:

W= p (V₂–V₁);

Звідси:

U = Q_p - p (V₂–V₁);

U = 126 - 101,310³ (1* 10^-2 – 1610^-3) = 481,8Дж

Відповідь: 481,8Дж

 1-2

Розрахуйте роботу ізотермічного (27С) розширення 1 моль вуглекислого газу від 2,24 до 22,4 л.

Розв’язок:

n = 1 моль, V₁ = 2,24л = 2,2410^-3 м³ , V₂ = 22,410^-3 м³ ,

Т = 27С = 300 K.

Работа ізотермічного розширення системи може бути визначена за рівнянням:

W = nRT 2,3 lg(V₂ /V₁);

W = 18,3143002,3 lg (22,410^-3 / 2,2410^-3) = 5736,66 Дж

Відповідь: 5736,66 Дж [1,2,3]

 

1.3 Задачі для розв’язування

 

1.     Шляхом нагрівання при постійному тиску 1,01310⁵ Па газу поглинуто 2093, 4 Дж теплоти. Визначити роботу, виконану газом , та зміну внутрішньої енергії цього газу ,  якщо він при цьому розширився  від 1 до 2 л.
2.     Один моль дифлуорметана (ідеальный газ) , взятій при 0С і 1 атм, нагрівають при постійному тиску до збільшення об’єму в три рази. Розрахуйте зміну ентальпії та внутрішньої енергії в цьому процесі , якщо залежність теплоємності дифлуорметану від температури меє такий вигляд: С_р = 20,26 + 7,5910^-2Т(Дж моль^-1К^-1)

(∆H = 33,7 кДж; ∆U = 29,1 кДж)

3.     Визначити зміну внутрішньої енергії при ізобарному (1,01310⁵ н/м²) випаровуванні 100 г води при 150С , якщо об’ємом рідкої води знехтувати. Теплота випаровуваня води при 150С дорівнює 2112,66 Дж/г.
4.     Азот (5 моль)  при 100С займає об’єм 0,025 м³. При нагріванні газу до 200С  було затрачено 14650 Дж. Визначити  С_р і кінцевий об’єм , якщо тиск газу при цьому не змінився. Визначити  роботу , зроблену азотом при ізотермічному (20С) його росширенні від 0, 015 до 0,1 м³, якщо початковий тиск становить 3,03910⁵ Па. Визначити кінцевий тиск?

(W = 657 Дж, р₂ = 45600 н/м²)

5.     При 298 К одноатомний газ в ідеальному стані ізотермічно та зворотно розширюється від 1,510³м³  до 1010³ м³, при цьому поглинається 96610³ Дж теплоти. Скільки моль газу приймало участь у цьому процесі.(205,51)
6.     Один моль ідеального газу, взятого при 25С і 100 атм, розширюється зворотно та ізометрично до 5 атм. Розрахуйте роботу, поглинену теплоту, зміни внутрішньої енергії та ентальпії в цьому процесі.
7.     Скільки необхідно затратити теплоти , щоб ізохорично нагріти  25г кисню від 0 до 50С? (811,85 Дж)
8.     Яку кількість теплоти необхідно для ізохоричного нагрівання 50 г вуглекислого агзу в інтервалі температур від 300 до 400С, якщо C_v = 40,2 Дж/моль? (4,56 кДж)
9.     В резервуарі місткістю 510^-2 м³ при 200 К і 0,510⁵ Па є азот. Визначити теплоту ,  що необхідно передати газу  , щоб його тиск дорівнював 210⁵ Па.В цих умовах вважати азот ідеальним газом. (18,7498 кДж)
10.     Один моль ксенона , при температурі 25С і 2 атм, расширюється адіабатично: а) зворотньо до 1 атм, б) проти тиску 1 атм. Якою буде температура в кожному випадку? ( а)225 К, б)238 К)
11.     Визначити роботу адіабатичного зворотнього розширення 3 моль аргону  від0,05 до 0,50 м³.  Початкова температура газу 298 К. (8,74510⁵Дж)
12.     При 298 К 110^-2 кг кисню стискається адіабатично від 810^-3 до 510^-3 м³.  Визначити кінцеву температуру ,  роботу процесу стискання , зміну внутрішньої енергії та зміну ентальпії , якщо С_v = 5/2R. (359, 637 К; -400,37 Дж; 400,34 Дж; 1,335 кДж)[ 5,6,2,3]

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Розділ 2.Формулювання  другого закону термодинаміки

 

Другий закон термодинаміки був сформульваний у середині 19-го століття , в ті часи , коли створювалася теоретична основа для конструювання і побудови теплових машин. Досліди Маєра й Джоуля встановили еквівалентність між тепловою й механічною енергіями (перший закон термодинаміки). Виникло питання про ефективність теплових машин. Експериментальні дослідження свідчили про те, що частина тепла обов'язково втрачається при роботі будь-якої машини.

У 1850-х , 1860-х роках  Клаузіус у низці публікацій розробив поняття ентропії. В 1865 році він нарешті обрав для нового поняття ім'я. Ці публікації довели також , що тепло неможливо повністю перетворити в корисну роботу , сформулювавши таким чином другий закон термодинаміки.

Статистичну інтерпретацію другому закону термодинаміки дав Больцман , запровадивши нове визначення для ентропії , яке базувалося на мікроскопічних атомістичних уявленнях.

Дру́гий закон термодина́міки — один із основних законів фізики , закон про неспадання ентропії в ізольованій системі. Він накладає обмеження на кількість корисної роботи , яку може здійснити тепловий двигун. На засадничому рівні другий закон термодинаміки визначає напрямок протікання процесів у фізичній системі - від порядку до безпорядку. Існує багато різних формулювань другого закону термодинаміки , загалом еквівалентних між собою.

Для системи із сталою температурою існує певна функція стану S — ентропія , яка визначається таким чином, що

Адіабатичний перехід із рівноважного стану A в рівноважний стан B можливий лише тоді, коли

S(B) ≥ S(A)

 Приріст ентропії у квазістаціонарному процесі дорівню

dS= δQ÷T         ,           де T — температура.[4,5,]

2.2 Приклади

2-1

Розрахуйте зміну ентропії при нагріванні 0,4 моль хлориду натрію від 20 до 850С. Мольна теплоємність хлориду натрію дорівнює:

С_р(NaCl_(тв)) = 45,94 +16,3210^-3Т ДжК^-1моль^-1,

С_р(NaCl_(ж)) = 66,53 ДжК^-1моль^-1. Температура плавлення хлориду натрію 800С, теплота плавлення 31,0 кДжмоль^-1.

 

Розв’язок

Загальна зміна ентропії складається із трьох складових

1. нагрівання твердого хлорида натрія від 20 до 800С,
2. плавлення,
3. нагрівання рідкого хлорида натрія від 800 до 850С.

S₁  =

S₂ =

S₃ =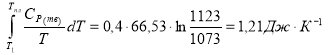

S = S₁ + S₂ + S₃, S = (28,94 + 11,6 + 1,21) ДжК^-1 = 41,75 ДжК^-1

Відповідь: 41,75 ДжК^-1

 2-2

Знайдіть зміни ентропії газу та навколишнього середовища, якщо n моль ідеального газу розшириться від об’єму V₁ до об’єму  V₂:

А) зворотньо,

Б) проти зовнішнього тиску р.

 

 

 

Розв’язок :

А) Зміну ентропії газу при зворотньому ізотермічному розширенні можна знайти за допомогою термодинамічного визначення ентропії з розрахунком теплоти розширення за першим законом:

S_r = Q_обр/T = nRlnV₂/V₁.

Так як розширення зворотнє , то загальна зміна ентропії Всесвіту дорівнює 0, тоді зміна ентропії зовнішнього середовища дорівнює зміні ентропії газу з протилежним знаком:

S_окр = -S_r = -n RlnV₂/V₁.

Б) зміна ентропії газу при незворотному розширенні проти зовнішнього тиску буде таким же,як і при зворотньому розширенні. Ентропія навколишнього середовища , яку можна знайти , розрахувавши за допомогою першого закону теплоту , що передалась системі:

S_окр = Q_окр/T = - W/Т = р(V₁ – V₂)/Т.

У даному висновку використано той факт , що U = 0 (так як температура постійна). Робота , що виконується системою проти постійного тиску, дорівнює:

W = р(V₂ – V₁),

а теплота , яку поглинуло зовнішнє середовище , дорівнює роботі , що зроблена системою ,з протилежним знаком. Загальна зміна ентропії газу і зовнішнього середовища більше 0 :

S = n RlnV₂/V₂ + р(V₁ – V₂)/Т  0

Що і є необхідним для незворотного процесу

2-3

Розрахуйте зміну ентропії 1000 г метанолу в результаті  його  замерзання при -105С. Теплота плавления твердого метанолу при -98С дорівнює 3160 Джмоль^-1. Теплоємність твердого і рідкого метанолу дорівнюють 55,6 і 81,6 ДжК^-1моль^-1,відповідно.

Розв’язок:

Незворотній процес кристалізації метанолу при температурі -105С можна представити у вигляді послідовнихзворотніх процесів:

А) нагрівання метанолу від –105С до температури кристаллізації (-98С),

Б) кристалізація метанолу при -98С,

Вохолодження метанолу від -98С до -105С:

 

175 К ж 2 тв

 1 3

168 К ж ? тв

Зміна ентропії в першому  і в третьому процесах (при зміні температури)розраховуємо за формулою:

S₁ = nC_р(Ж)lnT₂/Т₁, где n = m/М,

S₁ = (1000/32)81,6ln175/168 ДжК^-1 = 104,10 ДжК^-1,

S₃ = (m/М)C_р(тв)lnT₂/Т₁,

S₃ = (1000/32)55,6 ln168/175 ДжК^-1 = -70,93 ДжК^-1.

 

Зміна ентропії у другому процесі розраховується як для звичайного фазового переходу , враховуючи, що теплота при кристалізації виділяється:

S₂ = _крН/Т_кр,

S₂ = -(1000/32)3160/175 ДжК^-1 = -564,29 ДжК^-1.

Общее изменение энтропии равно сумме по этим трем процессам:

S = S₁ + S₂ + S₃, S = (104,10 - 564,29 – 70,93) ДжК^-1 =

= -531,12 ДжК^-1.

Відповідь: -531,12 ДжК^-1.

[ 5,3,6]

 

 

 

 

3.3 Задачі для роз’вязувння

 

3-1. Розрахуйте зміни ентропії при нагріванні 0,7 моль моноклінної сірки від  25 до 200С при тиску 1 атм. Мольна теплоемністьсірки дорівнює: С_р(S_(тв)) = 23,64 ДжК^-1моль^-1, С_р(S_(ж)) = (35,73 + 1,1710^-3Т) ДжК^-1моль^-1. Температура плавлення моноклінної сірки 119С, теплота плавлення 45,2 Джг^-1. (11,88 ДжК^-1)

3-2. Один кілограм води, при 0С, приведений у стан перегрітої пари з температурою 200С та тиском 1,01310⁵Па. Обчисліть зміну ентропії цього переходу , якщо теплота  води при випаровуванні при 100С становить 2257 Дж/г, питома теплоємність при тиску в 1,01310⁵Па дорівнює 1,968 ДжК^-1моль^-1. (7824,8 Дж)

3-3. Під тиском 19,610⁴ Па нагрівають 210^-3 м³ аргону до збільшення його об’єму до 1210^-3 м³. Яка зміна ентропії якщо початкова температура 373 К. (2,44 ДжК^-1моль^-1)

3-4. Обчисліть зміну ентропії при нагріванні 16 кг О₂ від  273 до 373 К при постійному об’ємі .Кисень вважати ідеальним газом .(3242,46 ДжК^-1)

3-5. 3,00 моль газоподібного СО₂ росширюється ізотермічно (в  тепловому контакті із зовнішнім середовищем, що має температуру 15,0С) проти постійного зовнішнього тиску 1,00 бар. Початковий і кінцевий об’єми газу становлять  10,0 л і 30,0 л,відповідно.Розрахуйте зміни ентропії:

а)системи, вважаючи  СО₂ ідеальним газом,

б)навколишнього середовища,

в)Всесвіту.

(S_сист=27,4ДжК^-1_,S_окр = -6,94ДжК^-1, S_всел=20,46ДжК^-1)

3-6. Знайдіть зміну ентропії газу та навколишнього середовища, якщо n молей ідеального газу розширюється ізотермічно від тиску р₁ до тиску р₂: а)зворотньо ; б) проти зовнішнього тиску р  р₂.

 

(а) S_газ = nRln(p₁/p₂), S_окр = -nRln(p₁/p₂),

б) S_газ = nRln(p₁/p₂), S_окр = nRр(1/p₁ - 1/p₂))

 

3-7.Розрахуйте зміни ентропії 1000 г води в результаті її замерзання при -5С. Теплота плавлення  льоду при 0С дорівнює 6008 Джмоль^-1. Теплоємність льоду та води  становлять 34,7 і 75,3 ДжК^-1моль^-1, відповідно. Поясніть, чому ентропія при замерзанні зменшується , хоча процес відбувається довільно .. (-1181Дж/К)

3-8. Обчисліть зміну ентропії під час процесу тверднення 1 моль

Переохолодження бензолу при бензолу  при 268 К, якщо при 278 К Н_{пл (бензолу)}=9956Джмоль^-1,С_{р бензолу(ж)}=127,3ДжК^-1моль^-1,

С_{р бензолу(тв)} = 123,6 ДжК^-1моль^-1, Р = cоnst = 1,0110⁵ Па. (35,61 ДжК^-1моль^-1)

3-9. Визначити зміну ентропії , якщо 10010^-3 кг води, взятої  при 273 К, перетворюється в пар при390 К. Питома вага води  при 373 К  дорівнює 2263,810^-3 Джкг^-1;  питома теплоємність рідкої води 4,2 Джкг^-1К^-1;  питома теплоємність пари при  постійному тиску 2,010^-3 Джкг^-1К^-1. (142 ДжК^-1моль^-1)

3-10. Азот (0,001 м³)  змішали з 0,002 м³  кисню при 27С  і тиску 1,01310⁵ Па.  Обчислити загальну зміну ентропії системи . (0,645 Дж)

[ 1,2,3]

 

 

 

 

 

 

 

Висновок

 

У розв'язанні тих чи інших питань термодинаміка використовує свій особливий –термодинамічний (феноменологічний) метод. Сутність цього методу  полягає  в узагальненні дослідних даних з подальшим використанням одержаних висновків (у вигляді законів) без урахування детальної будови розглядаємих систем. Особливістю термодинамічного методу є придатність його лише до систем, що складаються з дуже великої кількості окремих частинок (тобто метод має статистичний характер), а також можливість визначення лише імовірності розглядаємих процесів. Питання швидкості процесу термодинамічним методом визначити неможливо. Не зважаючи на свою обмеженість, термодинамічний метод більш точний, ніж статистичний та квантово-механічний методи дослідження, бо при його застосуванні не треба уводити спрощуючі припущення, які необхідні через складність реальних систем, вивчаємих методами статистичної чи квантової механіки.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Литература

 

1.Г.С. Каретников, И.В. Кудряшов. Сборник примеров и задач по физической химии. - М: Высшая школа, 1991 г.

2. И.И. Климов, А.И. Филько. Сборник примеров и задач по физической и коллоидной химии. – М: Просвещение, 1975 г.

3. В.В. Еремин, С.И. Каргов, И.А. Успенская, Н.Е. Кузьменко, В.В. Лунин. Основы физической химии. Теории и задачи. – М: Экзамен, 2005.

Лебідь В. І. Фізична хімія. Харків: Фоліо, 2005. – 478 с

4. Стромберг А.Г., Семченко Д.П. Физическая химия.– М.: Высш. Шко-ла, 1999.

5. Глазов В.М. Основы физической химии. – М.: Высш. Школа, 1981.

6. Краткий справочник физико-химических величин. / Под ред. А.А.Равделя, А.М.Понамарёвой. Л.: химия, 1999.

7. Кудряшов И.В. Сборник примеров и задач по физической химии.– М.: Высш. Школа, 1993.

8. Практикум по физической химии. / Под ред. И.В. Кудряшова. М.: Высш. Школа, 1986.