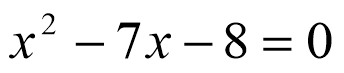Квадратні рівняння. Способи їх розв’язування.

Тема: Квадратні рівняння. Спо­соби їх розв’язування .

 

Мета: Узагальнити, систематизувати та поглибити знання учнів  про види квадратних рівнянь, його елементи та спо­соби їх розв’язування. Розвивати навички ус­ної лічби, обчислювальні навички, вміння засто­совувати набуті знання при розв’язуванні практичних завдань; сприяти активізації ро­зумової діяльності учнів. По­казати алгебраїчні способи розв’язування квадратних рівнянь на множині дійсних і комплексних чисел та мовою програму­вання Turbo Pascal.

Виховувати  інтерес до математики, ба­жання постійно поглиблювати свої математичні знання ,  вміння працювати з комп’ютером.

 

Тип: Бінарний урок з комп’ютерною підтримкою.

         Узагальнення й систематизація знань.

 

Засоби навчанням: Опорний конспект «Квадратні рівняння», настінна таблиця «Квадратні рівняння», персональний комп’ютер, електронна наочність  «Алгебра 7-9».

 

Девіз: «Алгебра – це, власне кажучи, аналіз рівнянь»

                                     Ж. Серре.

             «Рівняння – це золотий ключ, що відчиняє усі математичні сезами»

                                      С. Коваль .

 

 

 

І . Організаційний момент.

 

       Перевірити готовність класу до заняття. Учні 8 класу займають  місце за ком’ютерами, учні 11 класу – за партами.

Згодом вони поміняються  місцями . На дошці на­писані тема заняття, девіз, намальовано ребус, за­писані завдання для усного рахунку. У класі розміщені настінна таблиця «Квадратні рівняння», комп’ютери,  для кожного учня передбачено опорний конспект «Квадратні рівняння».

 

  II.  Мотивація навчальної діяльності.

 Узагальнити , систематизувати та поглибити знання учнів про види квадратних рівнянь, їх елементи, способи їх розв’язування на множині дійсних і комплексних чисел та мовою програму­вання Turbo Pascal.

    Проблемне завдання  –  це виконання випереджальної домашньої роботи,  що передбачає знайти шляхи розв’язання квадратних рівнянь з ве­ликими коефіцієнтами.

 

III.  «Математика – гімнастика розуму» .  О.В. Суворов.

 

    Усний рахунок. Обчислення раціональним способом за допомогою відомих алгоритмів.

 

1. Множення на 11:

72·11=792;

34·11= 374;

56·11= 616;

78·11= 858;

81·11= 891.

 

2. Множення на 101:

47·101= 47·100+47·1= 4747;

58·101= 5858;

92·101= 9292;

31·101=3131;

76·101= 7676.

 

 

 

 

 

 

3. Множення на число Шахразади. Воно ці­каве тим, що є добутком простих чисел 7·11·13.

 

347·1001=347347;

528·1001= 528528;

985·1001= 985985;

115·1001= 115115;

479·1001=479479.

 

4. Квадрати чисел, що закінчуються цифрою 5.

 

75²= 7·8·100+25= 5600+25=5625;

95²= 9025;

65²= 4225;

35²= 1225.

 

5. Розв’язати квадратні рівняння усно будь-яким способом:

 

x²+10x+25=0;

(x-3)²=16;

3y²-4y+1=0;

5x²-4x-1=0;

2x²+6x-8=0.

 

 

IV.  Трохи історії та теорії.

 

Рівняння ІІ  степеня  вавилонські матема­тики вміли розв’язувати ще 4 тис. років тому. Зго­дом їх також розв’язували у Китаї та Греції. 

 

 

 

1. Математики давньої Греції розв’язували квадратні рівняння геометрично. Наприклад, Евклід – при допомозі ділення відрізка в середньому і крайньому відношеннях. Особливу увагу квадратним рівнянням приді­ляв Мухамед аль- Хорезмі (ІХст.).

Формули коренів квадратного рівняння вивів Франсуа Вієт(1540 – 1603). Теорему тепер на­зи­вають його ім’ям, але від’ємних коренів він не розглядав.

            Сучасні способи розв’язування квадратних рівнянь поширилися завдяки працям Рене Декарта (1596 – 1650) та Ісаака Ньютона(1643- 1727).

 

2. «Алгебра – це, власне кажучи, аналіз рівнянь» Ж. Серре.

 

З допомогою персональних комп’ютерів та електронної програми «Алгебра 7 – 9», таблиць та опорних конспектів повторити теоретичний мате­ріал про види квадратних рівнянь, його елементи та способи їх розв’язування.

3. З метою узагальнення та систематизації знань розгадати кросворд та ребуси.

 

 

 

 

 

 

 

 

 

		9
	2			3				5
1
							8
						7
							6
		10
			4

 

 

 

 

1. Рівняння

виду

називається…

2. Як називаються числа a,b,c…

3. Що опреділяє корені квадратного рівняння…

4. Скільки коренів має квадратне рівняння, якщо D<0…

5. Квадратне рівняння,у якого b=0, або c=0 називається…

6. Квадратне рівняння,у якого є всі коефіцієнти,називається…

 

 

 

 

 

 

 

 

 

 

7. Рівняння,у якого a=1,називається…

8. Скільки коренів має рівняння,у якого D=0…

9. Скільки коренів має рівняння,у якого D>0…

10. Батько алгебри…   Ребус.   Щоб розгадати ребус, знайдіть додатній корінь рівняння

 

 

 

 

 

 

 

V.  Поміркуй і розв’яжи !

 

 « Рівняння  - це золотий ключ, що відчиняє усі математичні сезами».

 

 

 

 

 

 

      1) Розв’язати всіма відомими способами квадратне рівняння:

2х² – 8х +6 = о

 

   Учні 8 класу на дошці розв’язують  дане рівняння відомими їм способами:

• за допомогою дискримінанта;
• за формулою, коли І І коефіцієнт – парне число;
• за теоремою Вієта;
• за сумою коефіцієнтів, що дорівнюють 0;
• виділенням квадрата двочлена. 

А учні 11 класу розв’язують це рівняння з допомо­гою мови програмування Turbo Pascal.

 

Program rivnanna;

Var a, b, c, D, x1 ,x2: real;

  begin

    write('a:='); read(a);

    write('b:='); read(b);

    write('c:='); read(c);

       D:=b*b-4*a*c;

         if D<0

        then

       writeln ('No')

         else

           begin

             x1:=(-b+Sgrt(D))/(2*a);

        x2:=(-b-Sgrt(D))/(2*a);

writeln('NO');

writeln('x1=’. x1);

writeln('x2=’, x2);

  end

  end.

 

2) Розв’язання проблеми : знайти шляхи розв’язування квадратних рівнянь з вели­кими коефіцієнтами:

 

319 + 1988 + 1669 = 0

 

Усі учні 8 класу демонструють свої розв’язки на дошці. Учні 11 класу пока­зують розв’язання  цього рівняння за до­помогою мови програмування Turbo Pas­cal.

 

Висновок. Вміння складати програми, вміння використовувати ці програми на практиці дають можливість розв’язати будь-яке квадратне рівняння з допомо­гою комп’ютера.

 

3) Розв’язати рівняння 5 - + 1 = 0.

 

Дискримінант цього рівняння від’ємний, тому на множині дійсних чисел це рів­няння коренів не має. Але існують так звані комплексні числа (складені числа),  у полі яких дане рівняння має розв’язки, де = -1. Число, квадрат якого дорівнює -1, позначають буквою і ,  називають уяв­ною одиницею,  тобто і = -1.

Учні 11 класу розв’язують дане рівняння на множині комплексних чисел.

 

Висновок. Поглиблюючи математичні знання, розвиваючи свої математичні здібності, можна легше і швидше розв’язувати багато практичних завдань.

 

VI.Цікава математика.

 

Пропонується  розгадати фокус  «Жива ЕОМ»

Учень на дошці пише довільне шестицифрове число, число одиниць якого не менше двох, крім  того  всі цифри повинні бути різними. До цього числа  додамо ще декілька шестицифрових чи­сел, причому деякі з них придумають і напи­шуть учні. Всього треба додати п’ять шестицифрових чисел. Відповідь буде блискавична! Наприклад: 

 

                                                                                                                         519647

                                                                                                                         413798

                                                                                                                         586201

                                                                                                                         204346

                                                                                                                         795653

                                                                                                                        2519645

 

VII .  Підсумок заняття.

 

Можливості математики невичерпні. Тому слід серйозно нею займатись. Су­часна наука комп’ютеризована ,  вона тісно пов’язана з математикою. Комп’ютерна грамотність допоможе розв’язати багато питань сучасної науки та нашого бурхливого життя.