Лабораторна робота на тему "Визначення прискорення вільного падіння за допомогою нитяного маятника"

ЛАБОРАТОРНА РОБОТА

Тема: Визначення прискорення вільного падіння за допомогою нитяного маятника

Мета роботи: виготовити нитяний маятник, визначити за його допомогою прискорення вільного падіння; переконатися в справедливості формули Гюйґенса.

Обладнання: штатив із муфтою та лапкою, металева кулька (або тягарець) із петелькою, нитка завдовжки 1,5–2 м, вимірювальна стрічка, секундомір.

ТЕОРЕТИЧНІ ВІДОМОСТІ

Прискоренням вільного падіння називають прискорення, з яким тіло рухається до Землі, коли на нього діє тільки сила земного тяжіння.

Прискорення, з яким тіла падають на Землю, зумовлене силою їх притягання до неї. Притягання фізичних тіл одне до одного є загальною властивістю матерії й існує як між макроскопічними тілами (зірками, планетами), так і між мікроскопічними тілами (атоми, молекули). Узагальнюючи відомі експериментальні факти, Ньютон сформулював закон всесвітнього тяжіння.

Дві матеріальні точки притягуються одна до другої із силою F, прямо пропорційною їх масам m₁ і m₂ і обернено пропорційною квадрату відстані R між ними: (1)

де G – гравітаційна стала, що дорівнює 6,67×10^-11.

Гравітаційна стала чисельно дорівнює силі взаємодії двох матеріальних точок з масами 1 кг, що знаходяться одна від одної на відстані 1 м.

Формула (1) справедлива і для реальних тіл, що мають сферичну форму. У цьому випадку r – відстань між центрами сфер.

Гравітаційна взаємодія Землі з будь-яким тілом, що знаходиться біля її поверхні, проявляється в притягуванні його Землею. Якщо тіло знаходиться на висоті (h) від поверхні Землі, то на нього діє сила тяжіння (2)

де R – радіус Землі, приблизно рівний 6400 км; М – маса Землі; m – маса тіла.

Якщо h << R, то h можна знехтувати і формула (2) приймає вигляд:

. (3)

Цю ж силу можна виразити і через прискорення a, з яким тіло падає на Землю:

F = ma; (4)

Із формул (3) і (4) випливає:

. (5)

Оскільки G, M, R – сталі, то і прискорення, з яким тіла падають на Землю у вакуумі, є сталою величиною. Його позначають буквою g, а чисельно воно приблизно дорівнює 9,8 м/с²

Взагалі значення g залежить від висоти h над рівнем моря і географічної широти. Остання залежність зумовлена тією обставиною, що Земля являє собою "приплюснутий" з полюсів шар, що обертається. Внаслідок добового обертання Землі з кутовою швидкістю ω навколо власної осі, що проходить через її полюси, виникає відцентрова сила інерції, яка зменшує величину прискорення вільного падіння g.

Неідеальна кулеподібність Землі та її добове обертання зумовлює те, що величина g в різних місцях Землі змінюється від 9,8м/с² на полюсах, до 9,78м/с² на екваторі.

Періодом коливань називають час T, за який відбувається одне повне коливання.

Період Т при малих відхиленнях маятника залежить від довжини маятника l: (5).

Звідси: (6).

Таким чином, якщо відомі значення l і Т, то користуючись формулою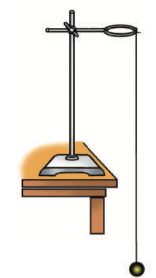 (6), можна знайти чисельне значення прискорення вільного падіння тіл g.

ХІД РОБОТИ

Підготовка до експерименту

1. Виготовте маятник (див.рисунок). Нитка маятника має бути досить довгою – кулька повинна майже торкатися підлоги.

Експеримент

1. Виміряйте довжину маятника (відстань від точки підвісу до центра кульки).

2. Відхиліть маятник від положення рівноваги на 5–8 см і відпустіть.
3. Виміряйте інтервал часу, за який маятник здійснює 20 коливань.
4. Повторіть дослід ще тричі, останнього разу (дослід 4) зменшивши довжину маятника вдвічі.

Таблиця 1

Опрацювання результатів експерименту

Частина 1. Вимірювання прискорення вільного падіння

1. За даними дослідів 1–3 визначте:

1) середній час 20 коливань: t_сер = (t₁ + t₂ + t₃) / 3;

2) період коливань маятника: T = t_сер / N;

3) прискорення вільного падіння:

2. Оцініть відносну похибку експерименту, порівнявши значення прискорення вільного падіння, отриманого в ході експерименту (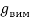), із табличним ():

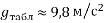Частина 2. Перевірка формули Гюйґенса

1. Для досліду 4 обчисліть період коливань маятника у два способи:

1) скориставшись означенням періоду: ;

2) скориставшись формулою Гюйґенса: ; вважайте, що .

2. Оцініть відносну похибку експерименту:

Аналіз експерименту та висновки

Проаналізувавши результати, зробіть висновок, у якому зазначте:

1) які досліди ви проводили;

2) які співвідношення були підтверджені;

3) які чинники вплинули на точність результатів експерименту.

Контрольні запитання

1. Закон всесвітнього тяжіння.
2. Сила взаємодії Землі з тілами, що знаходяться поблизу її поверхні.
3. Фізичний зміст гравітаційної сталої.