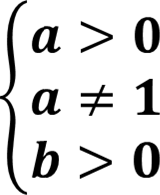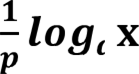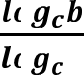Логарифми в дії: Практичні завдання та приклади.
|
показник степеня до якого необхідно піднести 𝐚, щоб отримати 𝐛
|
ВЛАСТИВОСТІ ЛОГАРИФМІВ
|
1. Основна логарифмічна тотожність 𝒂𝒍𝒐𝒈𝒂𝒃=b. 2. 𝒍𝒐𝒈𝒂𝒂 =1 3. 𝒍𝒐𝒈𝒂𝟏 = 𝟎 4. 𝒍𝒐𝒈𝒂xy = 𝒍𝒐𝒈𝒂𝒙 + 𝒍𝒐𝒈𝒂y (х>0, у>0 ) 5. 𝒍𝒐𝒈𝒂 𝒚 6.
|
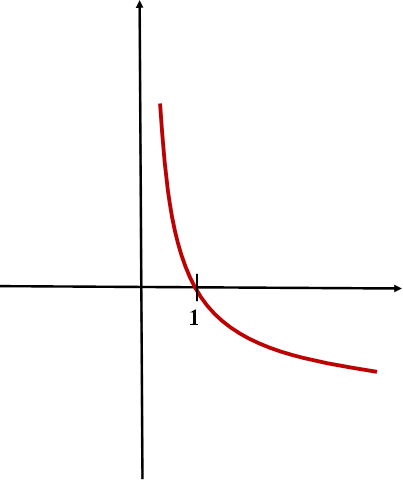
ГРАФІК ЛОГАРИФМІЧНОЇ ФУНКЦІЇ y=𝒍𝒐𝒈𝒂𝒙
|
0<a<1 |
|
a>1 |
|
|
|
|
ОСНОВНІ ТИПИ ЛОГАРИФМІЧНИХ РІВНЯНЬ
|
ТИП РІВНЯННЯ |
СПОСІБ РОЗВ»ЯЗАННЯ |
|
1. logax=c |
за означенням 𝒂𝒄=x. |
|
2. logax=logay |
x=y |
|
3. m𝒍𝒐𝒈𝟐𝒂𝐱 + 𝐛𝒍𝒐𝒈𝒂𝐱 + 𝐜 = 𝟎 |
заміна 𝒍𝒐𝒈𝒂𝐱 = 𝐭 → квадратне рівняння |
|
4. 𝒙𝒍𝒐𝒈𝒂𝒙+𝒎 =c |
логарифмування лівої і правої частини рівняння 𝒍𝒐𝒈𝒂𝒙𝒍𝒐𝒈𝒂𝒙+𝒎 =𝒍𝒐𝒈𝒂c → (𝒍𝒐𝒈𝒂x+m)𝒍𝒐𝒈𝒂x =𝒍𝒐𝒈𝒂c →р-ння 3. |
Обов»язкова перевірка отриманих коренів!!!
УВАГА! При використанні властивості 𝒍𝒐𝒈𝒂𝒙𝒑= p𝒍𝒐𝒈𝒂x (р- парне натуральне число) можна втратити корені!
СХЕМА РОЗВ»ЯЗУВАННЯ ЛОГАРИФМІЧНОЇ НЕРІВНОСТІ
|
1. ОДЗ 2. Розв»язування нерівності (див. основні типи логарифмічних нерівностей ) 3. Спільне п.1 і п.2 |
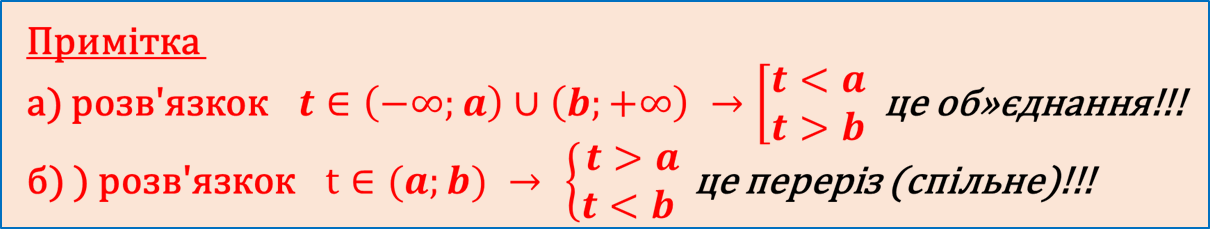
ОСНОВНІ ТИПИ ЛОГАРИФМІЧНИХ НЕРІВНОСТЕЙ
|
ТИП НЕРІВНОСТЕЙ |
СПОСІБ РОЗВ»ЯЗАННЯ |
|
1. logax > logay |
x>y (якщо а>1), x<y (якщо 0<а<1) |
|
2. logax>c |
𝒍𝒐𝒈𝒂x>c·1 → 𝒍𝒐𝒈𝒂x>c·𝒍𝒐𝒈𝒂𝐚 → 𝒍𝒐𝒈𝒂x>𝒍𝒐𝒈𝒂𝒂𝒄→ перехід до нерівності 1. |
|
3.m𝒍𝒐𝒈𝟐𝒂𝐱 + 𝐛𝒍𝒐𝒈𝒂𝐱 + 𝐜 < (>)𝟎 |
заміна 𝒍𝒐𝒈𝒂𝐱 = 𝐭, перехід до квадратичної нерівності |
|
𝟒. 𝒙𝒍𝒐𝒈𝒂𝒙+𝒎 >c |
логарифмуваня: 𝒍𝒐𝒈𝒂𝒙𝒍𝒐𝒈𝒂𝒙+𝒎 > 𝒍𝒐𝒈𝒂c → (𝒍𝒐𝒈𝒂x+m)𝒍𝒐𝒈𝒂x >𝒍𝒐𝒈𝒂c (якщо а>1) 𝒍𝒐𝒈𝒂𝒙𝒍𝒐𝒈𝒂𝒙+𝒎 < 𝒍𝒐𝒈𝒂c → (𝒍𝒐𝒈𝒂x+m)𝒍𝒐𝒈𝒂x <𝒍𝒐𝒈𝒂c (якщо 0<а<1) перехід до нерівності 3. |
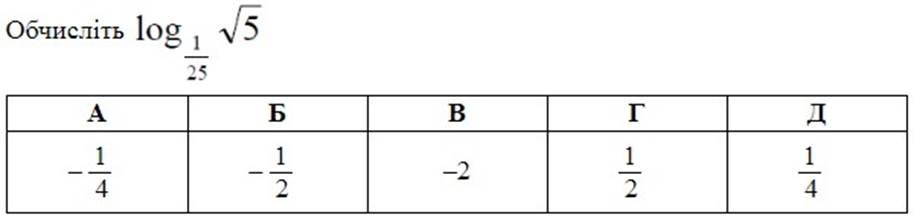 |
Розв`язання.
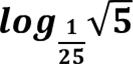
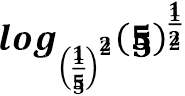 𝒍𝒐𝒈 𝟏 𝟓 = 𝒍𝒐𝒈
𝒍𝒐𝒈 𝟏 𝟓 = 𝒍𝒐𝒈
𝟐𝟓
Відповідь. А
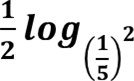
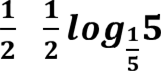
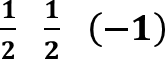
![]() = 𝟏𝟐 𝒍𝒐𝒈 𝟏 𝟐5 = 𝟏𝟐
= 𝟏𝟐 𝒍𝒐𝒈 𝟏 𝟐5 = 𝟏𝟐 ∙ 𝟏𝟐 𝒍𝒐𝒈𝟏𝟓 = 𝟐𝟏 ∙ 𝟏𝟐 ∙ −𝟏 = -𝟏𝟒
𝟓 𝟓
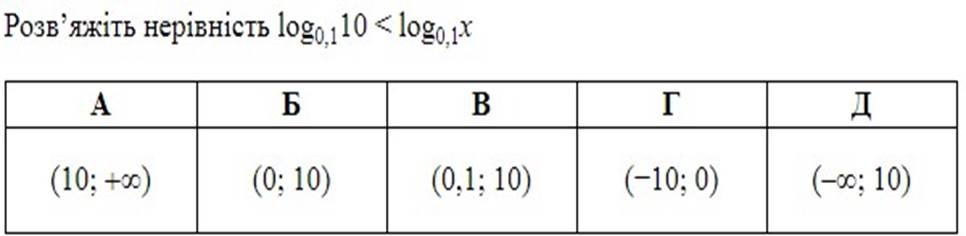
1. ОДЗ х>0
2. Оскільки 𝟎 < 𝟎, 𝟏 < 𝟏, то 𝟏𝟎 > х.
3. Спільне п.1 і п.2.
![]()
0 10
Відповідь. Б
Розв`язання.
Використаємо властивість логарифмів (перехід до іншої основи). Основу вибираємо довільну.
 |
𝒍𝒐𝒈𝟑𝟒 ∙ 𝒍𝒐𝒈𝟒𝟓 ∙ 𝒍𝒐𝒈𝟓𝟕 ∙ 𝒍𝒐𝒈𝟕𝟖𝟏 =
Відповідь. 4
Розв`язання.
 |
x+2 = 2x – a -x = -a-2 x = a+2. Корінь x = a+2 повинен задовольняти умови: x+2 >0 і 2x – a >0. Оскільки x+2 = 2x – a, то достатньо забезпечити виконання однієї з умов.
Наприклад x + 2 > 0, x > −2, а + 2 >−2, а > − 4.
Відповідь. -3
ЗНО-2008
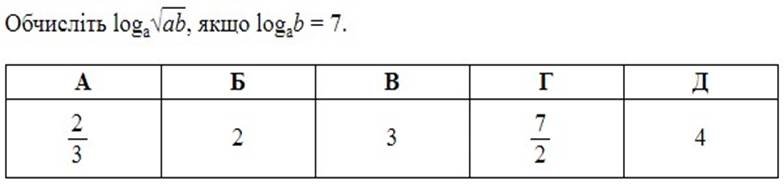
Розв`язання.
![]() 𝒍𝒐𝒈𝒂 𝒂𝒃 = 𝒍𝒐𝒈𝒂
𝒍𝒐𝒈𝒂 𝒂𝒃 = 𝒍𝒐𝒈𝒂![]() 𝒂 ∙ 𝒃
𝒂 ∙ 𝒃![]() = 𝟏𝟐
= 𝟏𝟐![]() ∙ 𝒍𝒐𝒈𝒂
∙ 𝒍𝒐𝒈𝒂![]() 𝒂 ∙ 𝒃
𝒂 ∙ 𝒃![]() = 𝟏𝟐 ∙
= 𝟏𝟐 ∙ ![]() 𝒍𝒐𝒈𝒂𝒂 + 𝒍𝒐𝒈𝒂𝒃
𝒍𝒐𝒈𝒂𝒂 + 𝒍𝒐𝒈𝒂𝒃![]() = 𝟏𝟐 ∙
= 𝟏𝟐 ∙ ![]() 𝟏 + 𝟕
𝟏 + 𝟕![]() = 4
= 4
Відповідь. Д
ЗНО-2009
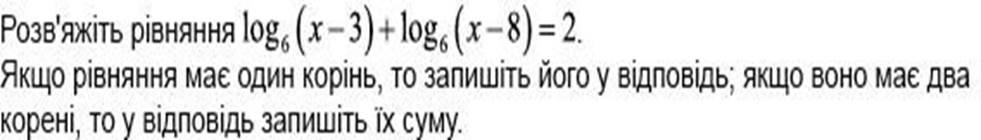
Розв`язання.
𝒍𝒐𝒈𝟔![]() 𝒙 − 𝟑
𝒙 − 𝟑![]() 𝒙 − 𝟖
𝒙 − 𝟖![]() = 𝒍𝒐𝒈𝟔 𝟑𝟔;
= 𝒍𝒐𝒈𝟔 𝟑𝟔;
𝒙2 − 𝟏𝟏𝒙 + 𝟐𝟒 = 𝟑𝟔;
𝒙2 − 𝟏𝟏𝒙 − 𝟏𝟐 = 𝟎;
З т-ми Вієта х𝟏 = −𝟏; х𝟐= 12.
Перевіркою встановлюємо, що тільки х𝟐 = 12 є коренем рівняння.
Відповідь. 12
ЗНО-2010

Розв`язання.
𝟏𝟖
![]()
![]()
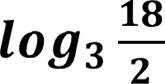
![]() 𝒍𝒐𝒈𝟑𝟏𝟖
𝒍𝒐𝒈𝟑𝟏𝟖 − 𝒍𝒐𝒈𝟑𝟐 = 𝒍𝒐𝒈𝟑 𝟐 = 𝒍𝒐𝒈𝟑𝟗 = 2
Відповідь. А
ЗНО-2010

Розв'язання.
1. ОДЗ х²+6х>0, 𝒙 ∈ (−∞; −𝟔) ∪ (𝟎 ; +∞)
2. ![]()
![]() 𝒍𝒐𝒈𝟏 𝒙2 + 𝟔𝒙
𝒍𝒐𝒈𝟏 𝒙2 + 𝟔𝒙![]() ≥ 𝒍𝒐𝒈𝟏𝟏𝟔. Оскільки 0 <
≥ 𝒍𝒐𝒈𝟏𝟏𝟔. Оскільки 0 < ![]() < 1, то х2 + 6𝑥 ≤ 16, х2+6𝑥 − 16 ≤ 𝟎
< 1, то х2 + 6𝑥 ≤ 16, х2+6𝑥 − 16 ≤ 𝟎
𝟒𝟒
𝒙 ∈ −𝟖; 𝟐![]() .
.
3. Спільне п.1 і п.2.
![]()
-8 -6 0 2
Цілі розв'язки: -8; -7; 1; 2
Відповідь. чотири цілі розв‘язки
ЗНО-2012
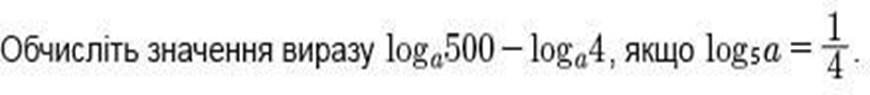
Розв'язання.
![]()
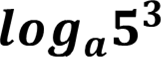 𝟓𝟎𝟎𝟑=
𝟓𝟎𝟎𝟑=
![]()
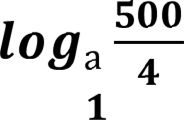 𝒍𝒐𝒈а𝟓𝟎𝟎
𝒍𝒐𝒈а𝟓𝟎𝟎 − 𝒍𝒐𝒈а𝟒 = 𝒍𝒐𝒈а 𝟒 = 𝒍𝒐𝒈а𝟏𝟐𝟓 = 𝒍𝒐𝒈𝒂𝟓
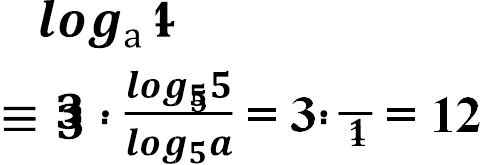
![]() = 3𝒍𝒐𝒈𝒂𝟓 𝒍𝒐𝒈𝒍𝒐𝒈𝟓𝒂𝟓 𝟏
= 3𝒍𝒐𝒈𝒂𝟓 𝒍𝒐𝒈𝒍𝒐𝒈𝟓𝒂𝟓 𝟏
![]() 𝟒
𝟒
Відповідь. 12
ЗНО-2015

Розв'язання.
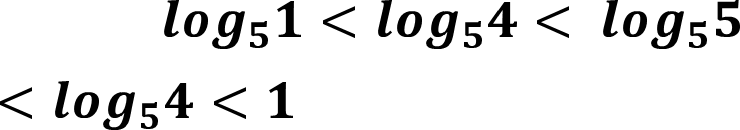 Оскільки 5>1, то 𝒍𝒐𝒈𝟓𝟏 < 𝒍𝒐𝒈𝟓𝟒 < 𝒍𝒐𝒈𝟓𝟓 Отже, 0< 𝒍𝒐𝒈𝟓𝟒 < 𝟏
Оскільки 5>1, то 𝒍𝒐𝒈𝟓𝟏 < 𝒍𝒐𝒈𝟓𝟒 < 𝒍𝒐𝒈𝟓𝟓 Отже, 0< 𝒍𝒐𝒈𝟓𝟒 < 𝟏
Відповідь. А
ПРОБНЕ ЗНО-2015

Розв'язання.
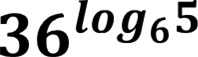
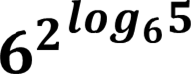
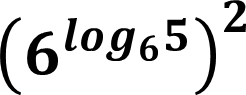
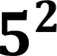 𝟑𝟔𝒍𝒐𝒈𝟔𝟓=𝟔𝟐𝒍𝒐𝒈𝟔𝟓= 𝟔𝒍𝒐𝒈𝟔𝟓 𝟐= 𝟓𝟐=25
𝟑𝟔𝒍𝒐𝒈𝟔𝟓=𝟔𝟐𝒍𝒐𝒈𝟔𝟓= 𝟔𝒍𝒐𝒈𝟔𝟓 𝟐= 𝟓𝟐=25
Відповідь. Г
ЗНО-2017

Розв'язання.
За рисунком видно, що розв‘язком нерівності є проміжок ![]() 𝟎; х𝟎
𝟎; х𝟎![]()
Зрозуміло, що х𝟎=𝟐𝒃, тому розв‘язком нерівності є проміжок ![]() 𝟎; 𝟐𝒃
𝟎; 𝟐𝒃 ![]() .
.
Відповідь. А
Приклад log𝟐𝟑![]() 𝟔 − 𝒙
𝟔 − 𝒙![]() − 𝒍𝒐𝒈𝟑
− 𝒍𝒐𝒈𝟑![]() 𝟔 − 𝒙
𝟔 − 𝒙![]() − 𝟏𝟐 > 𝟎
− 𝟏𝟐 > 𝟎
1. ОДЗ 6-х>0, х<6
2. ![]() Заміна 𝒍𝒐𝒈𝟑x=t t² - t -12 > 0 𝐭 ∈
Заміна 𝒍𝒐𝒈𝟑x=t t² - t -12 > 0 𝐭 ∈ ![]() −∞;−𝟑 ∪ 𝟒;+∞
−∞;−𝟑 ∪ 𝟒;+∞![]()
це записується ( об»єднання) ቈ𝒕 < −𝟑 𝒕 > 𝟒
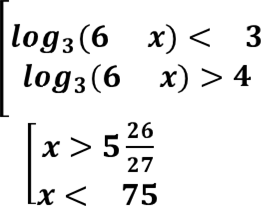
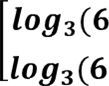
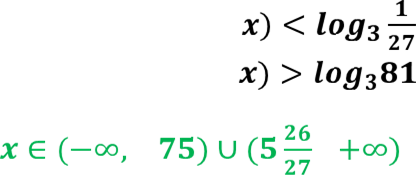 𝒍𝒐𝒈𝟑(𝟔
𝒍𝒐𝒈𝟑(𝟔 − 𝒙) < −𝟑 ቈ𝒍𝒐𝒈𝟑(𝟔 − 𝒙) < 𝒍𝒐𝒈𝟑𝟐𝟕𝟏
𝒍𝒐𝒈𝟑(𝟔 − 𝒙) > 𝟒 𝒍𝒐𝒈𝟑(𝟔 − 𝒙) > 𝒍𝒐𝒈𝟑𝟖𝟏
𝟐𝟔
𝒙 > 𝟓 𝟐𝟔
ቈ 𝟐𝟕 𝒙 ∈ (−∞; −𝟕𝟓) ∪ (𝟓 ; +∞)
𝒙 < −𝟕𝟓 𝟐𝟕
3. Спільне п.1 і п.2.
𝟏
![]()
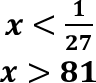 3>1, тому 𝟔
3>1, тому 𝟔 − 𝒙 < 𝟐𝟕
𝟔 − 𝒙 > 𝟖𝟏
![]()
-75 5𝟐𝟔 6
𝟐𝟕
𝟐𝟔
Відповідь ![]() −∞; −𝟕𝟓
−∞; −𝟕𝟓![]() ∪ (𝟓
∪ (𝟓 ![]() ; 6)
; 6)
𝟐𝟕


про публікацію авторської розробки
Додати розробку