Міністерство освіти і науки України

Департамент освіти і науки Київської обласної державної адміністрації

Київське обласне територіальне відділення МАН України

 

 

                                                                                                                  Відділення: Комп’ютерних наук Секція: Технології програмування

 

 

Лінійна функція та її графік. Автоматизоване обчислення відстані між точками на графіку лінійної функції. 

(мова PascalABCNET)

 

 

                                                                         Роботу виконала: 

Крицька Катерина Богданівна, учениця 9 класу 

Білоцерківська загальноосвітня школі I-III ступенів №7 ІМЕНІ

ГЕНЕРАЛ-ПОЛКОВНИКА

ГЕННАДІЯ ВОРОБЙОВА

Білоцерківської міської ради Київської області 

 

                                                                         Науковий керівник: 

Заєць Богдан Петрович , вчитель інформатики .

Білоцерківська загальноосвітня школі I-III ступенів №7 ІМЕНІ

ГЕНЕРАЛ-ПОЛКОВНИКА

ГЕННАДІЯ ВОРОБЙОВА

Білоцерківської міської ради Київської області 

 

 

Біла Церква – 2017

Відділення Комп’ютерних наук

Секція «Технології програмування»

«Лінійна функція та її графік. Автоматизоване обчислення відстані між точками

на графіку лінійної функції»

 

Автор: 

Крицька Катерина Богданівна,

учениця 9 класу 

Білоцерківська загальноосвітня школі I-III ступенів №7 ІМЕНІ ГЕНЕРАЛПОЛКОВНИКА ГЕННАДІЯ ВОРОБЙОВА Білоцерківської міської ради

Київської області   Науковий керівник: 

Заєць Богдан Петрович , вчитель інформатики 

Білоцерківська загальноосвітня школі I-III ступенів №7 ІМЕНІ ГЕНЕРАЛ-

ПОЛКОВНИКА ГЕННАДІЯ ВОРОБЙОВА Білоцерківської міської ради

 

Київської області 

 

_{Прикладна математика} — галузь математики, що розглядає застосування математичних знань в інших сферах діяльності. Прикладами такого застосування будуть: чисельні методи, математична фізика, математична хімія, лінійне програмування, оптимізація і дослідження операцій, моделювання суцільних середовищ. 

Предмет дослідження: У дослідженні реальних процесів і явищ функції відіграють особливу роль – математичних моделей. Найбільш важливим функціям математики дають власні назви. Однією з них є лінійна функція. 

Лінійною називають функцію, яку можна задати формулою виду y=kx+b, де x – аргумент, k і b – дані числа. 

Мета дослідження: Навчитися створювати інформаційні моделі задач для заданої предметної галузі, зокрема при розв’язування задач з інших навчальних предметів (алгебра), знаходити значення функції за даним значенням аргументу, будувати графік лінійної функції, з’ясовувати окремі характеристики функції за її графіком, створювати та редагувати програми, які містять  елементи графіки та анімації із застосуванням мови програмування PascalABC.NET, підключення та використання модуля Uses GraphABC, для створення графічних та анімаційних програм. 

 Результатом дослідження є програма (мова програмування Pascal), яка знаходить значення лінійної функції (виду y=a-b*х) за даним значення аргументу (x), будує на екрані графік лінійної функції, а також знаходить відстань між двома заданими точками на графіку функції  

Зміст

                          Вступ                                   Розділ 1       

                     Математичні функції                                                             

            1.1     Лінійна функція та її графік                                                     

            1.2     Обчислення відстані між двома точками                                 

                     Розділ 2                                                                                    

                     Мова програмування pascal                                                  

            2.1     pascalABC.net                                                                           

            2.2     Процедури графічної бібліотеки graphABC                             

                     Розділ 3                                                                                    

                     Автоматизація обчислень лінійної функції                          

            3.1     Значення функції                                                                      

            3.2     Графік функції                                                                         

            3.3     Обчислення відстані між двома точками                                 

                     Висновки                                                                                 

                     Список використаних джерел                                               

                     Додатки                                                                                   

 

                 

Розділ 1

Математичні функції

1.1 Лінійна функція та її графік

У дослідженні реальних процесів і явищ функції відіграють особливу роль – математичних моделей. Найбільш важливим функціям математики дають власні назви. Однією з них є лінійна функція. 

Лінійною називають функцію, яку можна задати формулою виду y=kx+b, де x – аргумент, k і b – дані числа.

Розглянемо дві лінійні функції, задані формулами y=2x-3 і y=-0,5x+2.  Будуємо графіки даних функцій.

Бачимо, що графік кожної з наведених функцій – пряма. Можна узагальнити приклади і довести таке твердження.

Графік кожної лінійної функції – пряма. І кожна пряма на координатній площині, не перпендикулярна до  осі абсцис, – графік деякої лінійної функції.

Для побудови прямої, якою є графік кожної лінійної функції, достатньо знати координати двох точок. Щоб побудувати графік функції                     y=-1,5x+3, треба скласти таблицю для двох будь-яких значень аргументу.

Лінійною називають функцію, яку можна задати формулою виду y=kx+b, де x – аргумент, k і b – дані числа.

Розглянемо дві лінійні функції, задані формулами y=2x-3 і y=-0,5x+2.  Будуємо графіки даних функцій.

Бачимо, що графік кожної з наведених функцій – пряма. Можна узагальнити приклади і довести таке твердження.

Графік кожної лінійної функції – пряма. І кожна пряма на координатній площині, не перпендикулярна до  осі абсцис, – графік деякої лінійної функції.

Для побудови прямої, якою є графік кожної лінійної функції, достатньо знати координати двох точок. Щоб побудувати графік функції                     y=-1,5x+3, треба скласти таблицю для двох будь-яких значень аргументу.

Задають функції найчастіше формулами (формула - formula), таблично (таблиця - table) або графічно. Графіком функції називається множина всіх точок координатної площини, абсциси яких дорівнюють значенням аргументу, а ординати - відповідним значенням функції. 

Наприклад, формула y=x² задає функцію, яка виражає відповідність між числами і їх квадратами. Якщо область визначення цієї функції - множина цілих чисел з проміжку [-3;3], то її можна задати таблицею:

x	- 3	- 2	- 1	0	1	2	3
y	9	4	1	0	1	4	9

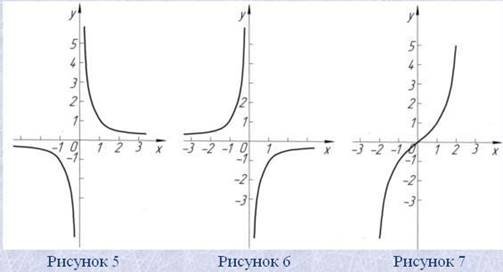
y=k/x – обернена пропорційність (inverse proportionality). Її графік – гіпербола (hyperbola). Коли k>0, вітки цієї гіперболи розміщені в І і ІІІ чвертях координатної площини (рис. 5), коли k<0 – в II и IV чвертях (рис. 6). Область визначення функції y=k/x множина R без числа 0, область значень – ця сама множина. 

Графік функції y=x3 зображено на рис. 7. Її область визначення і множина значень – множина R.

Графік функції  – одна вітка параболи (рис. 8). Її область визначення [0;+∞) і область значень [0;+∞).

Якщо змінна y залежить від x, то записують y=f(x). Символом f(a) позначають значення функції y=f(x) коли x=a. Нехай, наприклад, функцію задано формулою y=3x²-5. Можна записати і так: f(x)=3x²-5. У цьому випадку f(0)=3·0²-5=-5; f(1)=3·1²-5=-2; f(-2)=3·(-2)²-5=7 . 

Зауваження. Якщо y=f(x), то часто кажуть, що y – функція від x, тобто функцією називають змінну y. Однак здебільшого під функцією розуміють не одну залежну змінну, а відповідність між значеннями двох змінних. До того ж – не будь-яку відповідність, а однозначну, при якій кожному значенню змінної х відповідає єдине значення змінної y.

Перетворення графіків елементарних функцій Графіки функцій y=f(x) і y=f(-x) симетричні відносно осі x (рис. 9).

Щоб побудувати графік функції y=kf(x), треба графік функції y=f(x) розтягнути від осі x в k разів, якщо k>1, або стиснути його в k разів до осі x, якщо 0<k

Щоб отримати графік функції y=f(x)+n, треба графік функції y=f(x) перенести на n одиниць в напрямі осі y, якщо n>0 або в протилежному напрямі, якщо n<0.</k

Щоб отримати графік функції y=f(x-m), досить графік функції y=f(x) перенести на m одиниць в напрямі осі x, якщо m>0 або на -m одиниць в протилежному напрямі, якщо m<0 (рис. 10). 

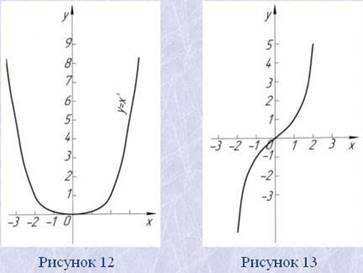
Функція, яка задається формулою y=ax²+bx+c, де a,b,c – довільні числа, а x – аргумент, називається квадратичною функцією. 

Малюнки 1-8

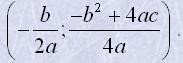Графік функції y=ax²+bx+c – парабола, координати вершин якої

 

Якщо a>0, то вітки параболи направлені вверх, якщо a<0, то вітки параболи направлені вниз. 

Щоб побудувати графік функції y=ax²+bx+c, можна знайти координати вершини параболи і ще кількох її точок, позначити їх на координатній площині і провести через них плавну лінію. Можна дотримуватись іншого способу: спочатку побудувати графік функції y=ax²+bx, а потім підняти або опустити його на |с| одиниць. Графік функції y=ax²+bx будувати неважко, оскільки він перетинає вісь абсцис у точках x=0 і x=-b/a, а її вершина знаходиться у

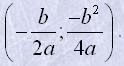точці

.

Описуючи властивості функції, звичайно починають з її області визначення. Область визначення функції (definitional domain) – проекція (projection) її графіка на вісь x; область значень функції (codomain) – проекція її графіка на вісь у (рис. 11).

Якщо для будь-яких двох значень аргумента більшому значенню аргумента відповідає більше значення функції, то таку функцію називають зростаючою (зростаюча функція – increasing function). Якщо для будь-яких двох значень аргумента більшому значенню аргумента відповідає менше значення функції, то таку функцію називають спадною (спадна функція – drop-down function). Наприклад, функції y=2x, y=x³ – зростаючі,

а функції – спадні. Графік зростаючої функції «іде вгору», а y=-2x,  спадної – «опускається вниз».

Можна також говорити про зростання чи спадання функції не на всій області визначення, а тільки на окремих проміжках.

Якщо графік функції симетричний (symmetric) відносно осі y, її називають парною (парна функція – even function). Якщо графік функції симетричний відносно початку координат, її називають непарною (непарна функція – odd function). 

Функція y=f(x) парна, якщо її область визначення симетрична відносно нуля і для кожного значення x з області визначення f(-x)=f(x). Функція y=f(x) непарна, якщо її область визначення симетрична відносно нуля і для кожного значення x з області визначення -f(-x)=f(x). 

Див.Додаток 1

 

1.2 Обчислення відстані між двома точками

Яким чином можна визначити відстань між точками? 

Див. додаток 2

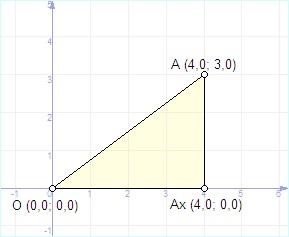
1.Знаходження відстані від точки до початку координат.(3хв)

Дано: А(4;3) Знайти: ОА.

Розв’язання.

Опустимо з точки А перпендикуляр на вісь абсцис. Розглянемо прямокутний Δ ААхО. У ньому катет ААх=3, ОАх=4. Це випливає зі значень координат точки А. Згідно теореми Піфагора  . Отже, ОА=5.

2.Знаходження відстані між двома точками, заданими координатами.(Викладення матеріалу можна здійснити по підручнику)(5хв)

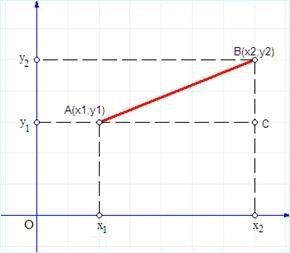
 Розглянемо, як це буде в загальному випадку. Нехай задано дві точки на координатній площині своїми координатами: А(х1;у1) і В(х2;у2). Для спрощення, нехай обидві точки лежать у І чверті, при чому х1< х2, y1< y2. Опустимо з кожної точки перпендикуляри на обидві осі. Розглянемо катети прямокутного Δ АСВ. Маємо, що АС= х2- х1, а ВС= у2- у1. Довжина гіпотенузи трикутника є шуканою відстанню, тому зручно використати теорему Піфагора, згідно якої  , а отже,  .

довели теорему про відстань між двома точками із заданими координатами:

Відстань між двома точками дорівнює кореню квадратному із суми квадратів різниць їх відповідних координат.

AB= AC² +BC² , а отже, AB= (x₂ −x₁)² +(y₂ −y₁)² .

Ми розглянули випадок, коли обидві точки лежать в І чверті, але суть доведення не змінюється, якщо точки А і В лежать в ІІ, ІІІ, IV або в різних чвертях.  (Див. додаток 2).

 

Розділ 2

Мова програмування pascal

2.1  pascalABC.net

Що таке мова програмування? Для того, щоб дати відповідь на це запитання, дамо спочатку відповідь на інше запитання: а що таке програмування, або в ще більш простому варіанті: що таке програма? Досить часто в житті ми вживаємо це слово, наприклад: програма телепередач на тиждень, програма підготовки до складання іспиту, індивідуальна програма для спортсмена при підготовці до змагань і т.д. В кожному з наведених прикладів у сказану фразу вкладено різний зміст, але загалом суть залишається тією ж: це послідовність дій (телепрограм на кожен день тижня, вивчення порцій (параграфів) навчального матеріалу при підготовці до іспиту, норми та види щоденного навантаження спортсмена ), точно виконуючи яку виконавець досягне поставленої перед ним задачі. У цьому розумінні термін “програма” дещо схожий до терміну “алгоритм”, але нашим завданням не є вияснення популярного запитання “хто є хто”, тому у нашому розумінні слово програма надалі писатиметься без лапок і буде являти собою систему послідовних команд для ПЕОМ для розв’язання кожної конкретної задачі.

Ми будемо розглядати мову Паскаль. Перші відомості про мову Паскаль були опубліковані в 1971 році. Його автор професор Інституту інформатики Швейцарської вищої політехнічної школи Ніклаус Вирт. Мова названа на честь видатного французького фізика, математика і філософа Блеза Паскаля.

Своєї величезної популярності, у даний час, Паскаль зобов'язаний американській фірмі BORLAND, що створила діалект мови Турбо Паскаль, розширивши стандартний Паскаль додатковими можливостями і створивши дуже зручну і швидку програму-транслятор.

Склад мови.

Звичайна розмовна мова складається з чотирьох основних елементів: символів, слів, словосполучень і речень. Мова програмування містить подібні елементи, тільки слова називають елементарними конструкціями, словосполученнявиразами, речення-операторами. Символи, елементарні конструкції, вирази й оператори складають ієрархічну структуру, оскільки елементарні конструкції утворяться з послідовності символів, вирази – це послідовність елементарних конструкцій і символів, а оператор – послідовність виразів, елементарних конструкцій і символів.

Опис мови є опис чотирьох названих елементів. Опис символів полягає в перерахуванні припустимих символів мови. Під описом елементарних конструкцій розуміють правила їхнього утворення. Опис виразів – це правила утворення будь-яких виразів, що мають зміст у даній мові. Опис операторів складається з розгляду усіх типів операторів, припустимих у мові. Опис кожного елемента мови задається його СИНТАКСИСОМ і СЕМАНТИКОЮ. Синтаксичні визначення встановлюють правила побудови елементів мови. Семантика визначає зміст і правила використання тих елементів мови, для яких були дані синтаксичні визначення.

СИМВОЛИ мов – це основні неподільні знаки, якими пишуться всі тексти мовою.

ЕЛЕМЕНТАРНІ КОНСТРУКЦІЇ – це мінімальні одиниці мови, що мають самостійний зміст. Вони утворяться з основних символів мови.

ВИРАЗ в алгоритмічній мові складається з елементарних конструкцій і символів, воно задає правило обчислення деякого значення.

ОПЕРАТОР задає повний опис деякої дії, що необхідно виконати. Для опису складної дії може знадобитися група операторів. У цьому випадку оператори поєднуються в СКЛАДЕНИЙ ЧИ ОПЕРАТОРИЙ БЛОК.

Дії, задані операторами, виконуються над ДАНИМИ. Речення алгоритмічної мови, у яких даються відомості про типи даних, називаються ОПИСАМИ операторів, які не виконуються.

Об'єднана єдиним алгоритмом сукупність описів і операторів утворює ПРОГРАМУ.

    Приклад запису простої програми:          Program TRIANG;           var A, B, C, S, P: Real;           begin

           Read(A,B,C);

           WriteLn(A,B,C);

            P:=(A+B+C)/2;

S:=Sqrt(P*(P-A)*(P-B)*(P-C));            WriteLn('S=',S:8:3)           end.

    Program - це заголовок програми, що вказує її ім'я. Рекомендують вказувати заголовок програми, щоб уже при першому знайомстві з її текстом можна було отримати інформацію про її призначення. Потрібно відмітити, що заголовок програми, що слідує, за словом PROGRAM є ідентифікатором і володіє всіма його властивостями. Крім цього, заголовок програми обов’язково повинен починатись з латинської літери, а далі можуть знаходитись символи, допустимі для алфавіту Pascal.

Label    -        підрозділ,   в        якому          вказується список        усіх   міток, що використовуються в програмі. Якщо міток у програмі немає, то підрозділ LABEL не вказуємо.

    Const - підрозділ опису констант. Якщо в програмі будуть застосовуватись константи, то їх імена та значення (після знаку рівності) вводять в розділі Const. В інших випадках цей підрозділ не вказується. Слід відмітити, що стандартні константи, прийняті в Pascal, не потрібно описувати в даному розділі.

    Type - підрозділ опису користувацьких типів даних. В цьому підрозділі переважно вказують складні та нестандартні типи даних. Якщо такі типи в програмі не використовують, то даний підрозділ не вказується.

    Var - підрозділ опису всіх змінних, що використовуються в програмі. Потрібно відмітити, що всі змінні, що використовуються в програмі, обов'язково повинні бути описані в підрозділі var. Це єдиний підрозділ розділу описів та узгоджень, який обов’язково повинен бути представлений у кожній Pascal-програмі.

    Розділ текстів процедур та функцій вказується лише у випадку, якщо в програмі використовуються нестандартні процедури та функції, що створені самим користувачем (якщо вони не описані в одному з модулів вказаних у розділі USES). Потрібно відмітити, що процедури та функції - це спеціальним чином оформлені послідовності команд (у вигляді підпрограми). Доступ до цієї підпрограми може здійснюватись з будь-якого місця основної програми, а також з будь-якої процедури та функції, що описані нижче по тексту програми.

    Розділ операторів - це розділ основного блоку програми. В цьому розділі знаходиться основний текст програми. Починається цей розділ словом begin і закінчується словом end, після якого слідує крапка.

 

 

 

 

 

 

 

 

2.2 Процедури графічної бібліотеки graphABC

Uses - цей підрозділ вказує назви модулів та бібліотек, що потрібно підключити до програми. Поняття “модуль”, “бібліотека”, “блок” складають основу термінології програмування на Pascal. Модуль представляє собою замкнутий блок, що має своє ім’я, компілюється окремо і підключається до вашої програми, як ніби “чорна скринька” із набором певних (описаних у ньому) процедур, функцій, типів даних, констант і т.д. Бібліотека представляє собою набір таких модулів. Якщо модулі в програмі не потрібно використовувати (не використовується процедури, функції і т.д., що описані в модулі), то цей підрозділ не вказуємо. Потрібно відмітити, що оператор USES може використовуватись в програмі лише один раз, при цьому в нього є чітко визначене місце (він знаходиться поперед усіх операторів та підрозділів (крім заголовка програми та директив компілятора)).

Модуль GraphABC є простою графічну бібліотеку і призначений для створення несобитійних графічних і анімаційних програм в процедурному і частково в об'єктному стилі. Малювання здійснюється в спеціальному графічному вікні, можливість малювання в декількох вікнах відсутній. Крім цього, в модулі GraphABC визначені найпростіші події миші і клавіатури, що дозволяють створювати елементарні подієві програми. Основна сфера використання модуля GraphABC - навчання.

Модуль GraphABC заснований на графічній бібліотеці GDI +, але запам'ятовує поточні перо, кисть і шрифт, що дозволяє не передавати їх в якості параметрів при виклику графічних примітивів. До властивостей пера, пензля і шрифту можна отримувати доступ як в процедурному, так і в об'єктному стилі. Наприклад, для доступу до кольору поточного пера використовується процедура SetPenColor (c) і функція PenColor, а також властивість Pen.Color.

У модулі GraphABC можна управляти самим графічним вікном і компонентом GraphABCControl, на якому здійснюється малювання. За замовчуванням компонент GraphABCControl займає всю клієнтську частину графічного вікна, проте, на графічне вікно можна додати елементи управління, зменшивши область, займану графічним компонентом (наприклад, так зроблено в модулях Robot і Drawman).

Для роботи з малюнками використовується клас Picture, що дозволяє малювати на собі ті ж графічні примітиви, що і на екрані.

 

Режим блокування малювання на екрані (LockDrawing) дозволяє здійснювати промальовування лише у позаекранного буфері, після чого за допомогою методу Redraw відновлювати все графічне вікно. Даний метод використовується для прискорення анімації і створення анімації без мерехтіння.

 

У модулі GraphABC визначено ряд констант, типів, процедур, функцій і класів для малювання в графічному вікні

 

                 

 

 

Розділ 3

Автоматизація обчислень лінійної функції

3.1 Значення функції

 

 

 

ЗАВДАННЯ: написати програму (мова програмування Pascal), яка знаходить значення лінійної функції (виду y=a-b*х) за даним значення аргументу (x), будує на екрані графік лінійної функції.

 

             

       Завдання поділимо на кілька  частин:

•      напишемо програму, яка знаходить значення лінійної функції (виду y=3-2*х) за даним значення аргументу (x)

•      змоделюємо на екрані графік лінійної функції (виду y=3-2*х) 

•      змінимо програму, щоб на екрані будувався графік лінійної функції (виду y=а-b*х)

1 напишемо програму, яка знаходить значення лінійної функції (виду y=2*х-3) за даним значення аргументу (x)

 в програмі використаємо модуль GraphABC.  Це проста графічна бібліотека і призначена для створення графічних і анімаційних програм. Малювання здійснюється в спеціальному графічному вікні , можливість малювання в декількох вікнах відсутня.

      Запустимо PascalABC.NET (Пуск/Усі програми/ PascalABC.NET/ PascalABC.NET)

 

 Для зручності користувача програми введемо змінну «n», яка дає можливість вказувати кількість значень аргументу «х» (в межах від –х до

+х). Наприклад, якщо n=3, то зміна «х» приймає значення

 -3; -2; -1; 0; 1; 2; 3.  тобто 2*n+1 значень (+1 враховуємо «0»).

 Значення змінних «x» та «y»  запишемо у вигляді одновимірного масиву. Одновимірний масив — це послідовність однотипних даних (у нашому випадку – цілих чисел). Опис масиву:

x,y:array[1..200] of integer;  n:integer;

максимальна кількість значень змінних «x» та «y» = 200 (n<=199). Будемо вважати, що користувач обмежиться цією кількістю значень.

Наприклад, якщо n=3, то зміна «х[i]» приймає значення: x[1]=-3; x[2]=-2 і т. п.

відповідно обчислимо значення y[1] для x[1], y[2] для x[2] і т. п.

      Використаємо оператор writeln() для опису призначення програми:: writeln(' Програма для малювання графіка функції вигляду y=3-2*x '); writeln(' введіть кількість значень змінної  "x"  (програма визначить значення  в діапазоні від -х до +х)');

 

read(n);

 

writeln('x= ',n);

 Для введення значень аргументу x[i] в масив використаємо оператор циклу: x[1]:=-n; for i:=2 to n+n+1 do begin x[i]:=x[i-1]+1; end; виведемо результат на екран:

 

for i:=1 to n+n+1 do begin

writeln('x[',i,']= ',x[i]); end; 

 

      Програма має вигляд:

 

Program demo_func;

Uses GraphABC; 

 

var n,i:integer;

 

x,y:array[1..200] of integer;

 

Begin

Window.Clear(clGreen); 

writeln(' Програма для малювання графіка функції вигляду y=3-2*x ');

 

writeln(' введіть кількість значень змінної "x" = (програма визначить  значення  в діапазоні від -х до +х)');

 

read(n);

 

writeln('x= ',n);

 

x[1]:=-n; for i:=2 to n+n+1 do begin x[i]:=x[i-1]+1; end; 

 

 

for i:=1 to n+n+1 do begin

write('x[',i,']= ',x[i],'  '); end;  end.

 

 

Window.Clear(clGreen); (викликає процедуру, яка очищує вікно зеленим кольором)

 

      Для запуску програми на виконання потрібно виконати команду Програма/Виконати

 

       в спеціальному графічному вікні введемо початкові дані:

 

 

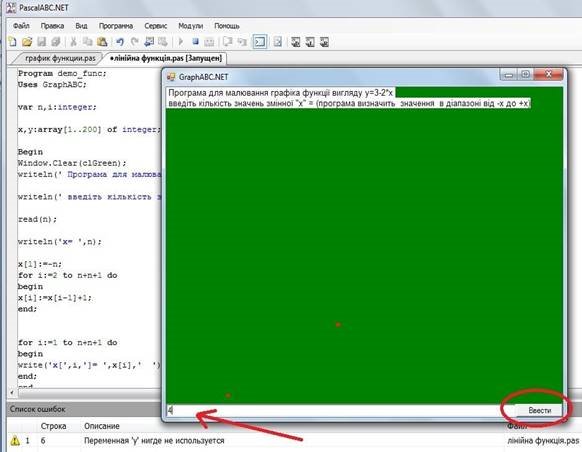
отримаємо результат:

 

 

             

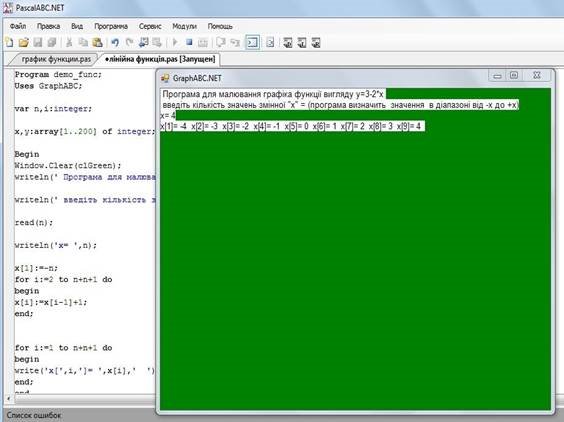
          Тепер для кожного x[i] розрахуємо y[i] (y[1]=3-2*x[1], y[2]=3-2*x[2] і т.п.).

Використаємо оператор циклу:

 

writeln (' значення змінної y '); for i:=1 to n+n+1 do begin

y[i]:= 3-2*x[i]; end; виведемо значення y[i] на екран:

 

for i:=1 to n+n+1 do begin

write('y[',i,']= ',y[i],'  ');

end;

      Програма має вигляд:

Program demo_func;

Uses GraphABC; 

 

var n,i:integer;

 

x,y:array[1..200] of integer;

 

Begin

Window.Clear(clGreen); 

writeln(' Програма для малювання графіка функції вигляду y=3-2*x ');

 

writeln(' введіть кількість значень змінної "x" = (програма визначить  значення  в діапазоні від -х до +х)');

 

read(n);

 

writeln('x= ',n);

 

x[1]:=-n; for i:=2 to n+n+1 do begin x[i]:=x[i-1]+1; end; 

 

 

for i:=1 to n+n+1 do

begin

write('x[',i,']= ',x[i],'  '); end;  writeln; writeln (' значення змінної y '); for i:=1 to n+n+1 do begin y[i]:=3-2*x[i]; end; for i:=1 to n+n+1 do begin

write('y[',i,']= ',y[i],'  '); end; 

 

end.

 

      Запустимо на виконання:

 

             

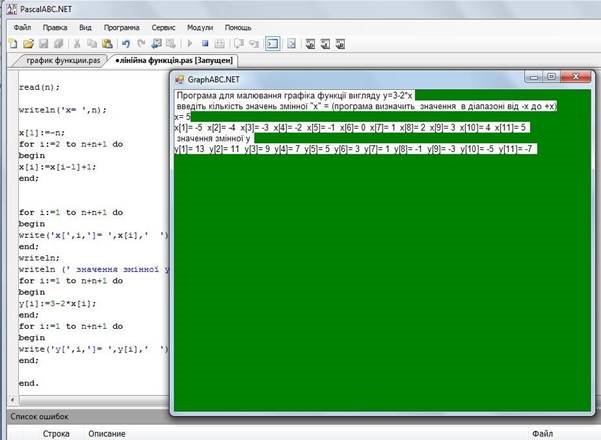
3.2 Графік функції

змоделюємо на екрані графік лінійної функції (виду y=3-2*х)

 В графічному вікні будемо використовувати значення х (від 0 до 600), а y (від 0 до 500). Точка з координатами х=0; у=0 знаходиться у лівому верхньому куті вікна.

Намалюємо посередині графічного вікна (приблизно) декартову систему координат.

Задамо колір пера. Використаємо процедуру procedure SetPenColor(c:

Color); використаємо червоний колір.

Щоб намалювати вісь «Х», використаємо процедуру procedure LineTo(x,y: integer); малює відрізок від заданої точки до точки (х,у).

Щоб вісь «Х» проходила посередині вікна, значення «Y» буде сталим (0<Y<500, тому Y=250). Зміна «Х» приймає значення 0<X<600, тому лінію намалюємо для «х» від 10 до 590 (наприклад).

Використаємо процедуру procedure MoveTo(x,y: integer); (задає початок малювання з точки  (х,у).

Додамо в програму рядки:

 

MoveTo(10,250); (перенесли перо в точку х=10, у=250)

LineTo(590,250); (малюємо пряму лінію з точки х=10, у=250 до точки х=590, у=250).

      Програма має вигляд:

Program demo_func;

Uses GraphABC; 

 

var n,i:integer;

 

x,y:array[1..200] of integer;

 

Begin

Window.Clear(clGreen); 

writeln(' Програма для малювання графіка функції вигляду y=3-2*x ');

 

writeln(' введіть кількість значень змінної "x" = (програма визначить  значення  в діапазоні від -х до +х)');

 

read(n);

 

writeln('x= ',n);

 

x[1]:=-n; for i:=2 to n+n+1 do begin x[i]:=x[i-1]+1;

end; 

 

 

for i:=1 to n+n+1 do begin

write('x[',i,']= ',x[i],'  '); end;  writeln; writeln (' значення змінної y '); for i:=1 to n+n+1 do begin y[i]:=3-2*x[i]; end; for i:=1 to n+n+1 do begin

write('y[',i,']= ',y[i],'  '); end; 

SetPenColor(clRed);

 

 MoveTo(10,250);

    LineTo(590,250); 

    

end.

      Запустимо на виконання:

 

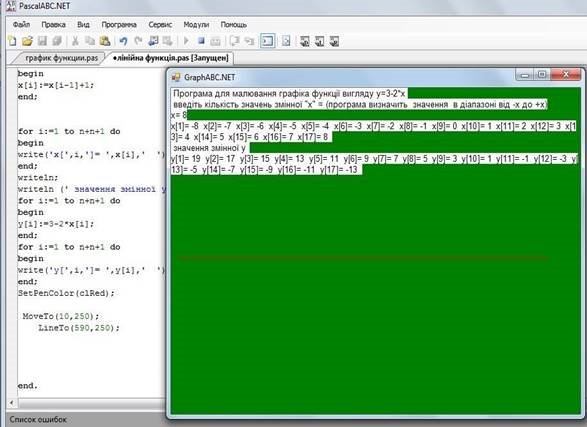
      Тепер намалюємо вісь «Y»:

MoveTo(300,10); (перенесли перо в точку х=300, у=10)

 

LineTo(300,450); (малюємо пряму лінію з точки х=300, у=10 до точки х=300, у=450).

(середина вікна – значення х=300)          В результаті:

 

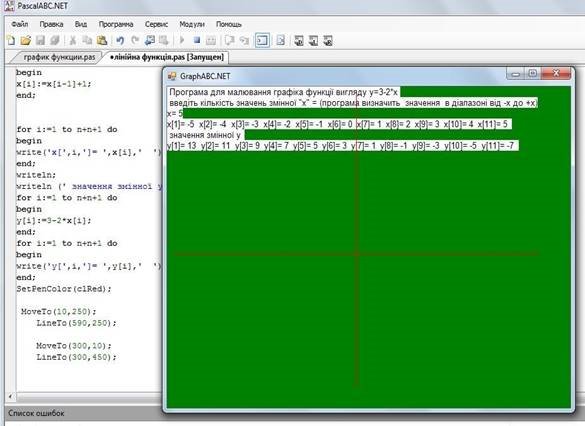
      Підпишемо    вісь     «Х»     та     «Y».     Використаємо    процедуру    procedure

TextOut(x,y: integer; s: string); (виводить на екран рядок з текстом «S», з координатами лівого верхнього кута х,у).

Додамо в опис змінних s1,s2:string; Задамо значення:

s1:=' X ';     s2:=' Y ';

   TextOut(590,250,s1);

     TextOut(300,10,s2);

 

      Програма має вигляд:

Program demo_func;

Uses GraphABC; 

 

var n,i:integer; s1,s2:string; x,y:array[1..200] of integer;

 

Begin

Window.Clear(clGreen); 

writeln(' Програма для малювання графіка функції вигляду y=3-2*x ');

 

writeln(' введіть кількість значень змінної "x" = (програма визначить  значення  в діапазоні від -х до +х)');

 

read(n);

 

writeln('x= ',n);

 

x[1]:=-n; for i:=2 to n+n+1 do begin x[i]:=x[i-1]+1; end; 

 

 

for i:=1 to n+n+1 do begin

write('x[',i,']= ',x[i],'  '); end;  writeln;

writeln (' значення змінної y '); for i:=1 to n+n+1 do begin

y[i]:=3-2*x[i]; end; for i:=1 to n+n+1 do begin

write('y[',i,']= ',y[i],'  '); end; 

 Sleep(5000);

Window.Clear(clGreen); 

SetPenColor(clRed);

 

 MoveTo(10,250);

    LineTo(590,250); 

    

    MoveTo(300,10); LineTo(300,450);

    s1:=' X '; s2:=' Y ';

    TextOut(590,250,s1);

     TextOut(300,10,s2);

 

   

 

end.

      Запустимо на виконання:

 

Sleep(5000); - затримка мс.

      Введемо змінні (позначають  початок координат в нашій системі):

x0:=300; y0:=250;        Задамо значення змінних х1,у1,х2,у2: x1:=x[1]+x0; (врахували «зсув» початку координат на х0,у0) if y[1]<=0 then  y1:=-y[1]+y0 else y1:=-y[1]+y0; (для  «у» змінимо знаки на протилежні (додатні значення у верхній частині вікна)

 

    SetPenColor(clGold);

    

    MoveTo(x1,y1); (перемістили перо на першу точку х1,у1)     for i:=2 to n+n+1 do     begin     x2:=x[i]+x0;

if y[і]<=0 then  y2:=-y[і]+y0 else y2:=-y[і]+y0;

    

LineTo(x2,y2);     end;

(в середині циклу змінюємо х2,у2 та малюємо лінії)            Програма має вигляд:

Program demo_func;

Uses GraphABC; 

 

var n,i,x0,y0,x1,y1,x2,y2:integer; s1,s2:string;

 

x,y:array[1..200] of integer;

 

Begin

Window.Clear(clGreen); 

writeln(' Програма для малювання графіка функції вигляду y=3-2*x '); writeln(' введіть кількість значень змінної "x" = (програма визначить значення  в діапазоні від -х до +х)');

 

read(n);

 

writeln('x= ',n);

 

x[1]:=-n; for i:=2 to n+n+1 do begin x[i]:=x[i-1]+1; end; 

 

 

for i:=1 to n+n+1 do begin

write('x[',i,']= ',x[i],'  '); end;  writeln;

writeln (' значення змінної y '); for i:=1 to n+n+1 do begin y[i]:=3-2*x[i]; end;

for i:=1 to n+n+1 do begin

write('y[',i,']= ',y[i],'  '); end; 

 Sleep(5000);

Window.Clear(clGreen); 

SetPenColor(clRed);

 

 MoveTo(10,250);

    LineTo(590,250); 

    

    MoveTo(300,10); LineTo(300,450);

    s1:=' X ';     s2:=' Y ';

    TextOut(590,250,s1); TextOut(300,10,s2); x0:=300; y0:=250; x1:=x[1]+x0;

if y[1]<=0 then  y1:=-y[1]+y0 else y1:=-y[1]+y0;

    SetPenColor(clGold);

    

    MoveTo(x1,y1);     for i:=2 to n+n+1 do begin     x2:=x[i]+x0;

    if y[і]<=0 then  y2:=-y[і]+y0 else y2:=-y[і]+y0;     LineTo(x2,y2);     end;

   

 

end.

      Запустимо програму:

 

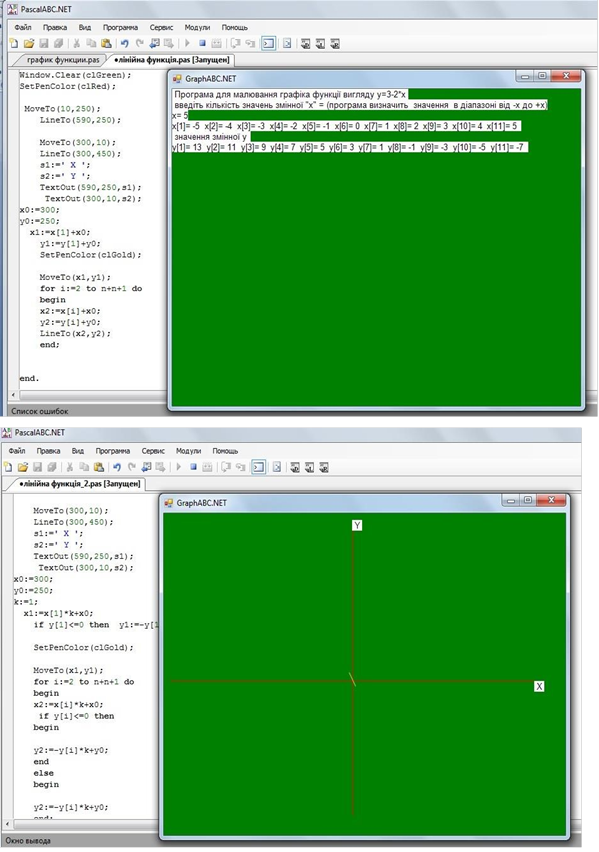
 Програма малює лінію з кроком 1. Збільшимо зображення нашої функції в 10 разів (крок між точками збільшимо на 10). Введемо коефіцієнт «k». Початкове значення задамо k:=10; змінимо програму:

x1:=x[1]*k+x0; x1:=x[1]*k+x0;

    if y[1]<=0 then  y1:=-y[1]*k+y0 else y1:=-y[1]*k+y0;

   

    SetPenColor(clGold);

    

MoveTo(x1,y1);     for i:=2 to n+n+1 do     begin     x2:=x[i]*k+x0;

     if y[i]<=0 then   y2:=-y[i]*k+y0 else  y2:=-y[i]*k+y0;

    

   

LineTo(x2,y2);     end;

   

      Запустимо на виконання:

 

 

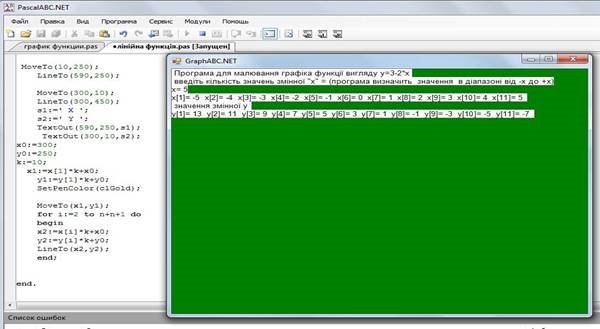
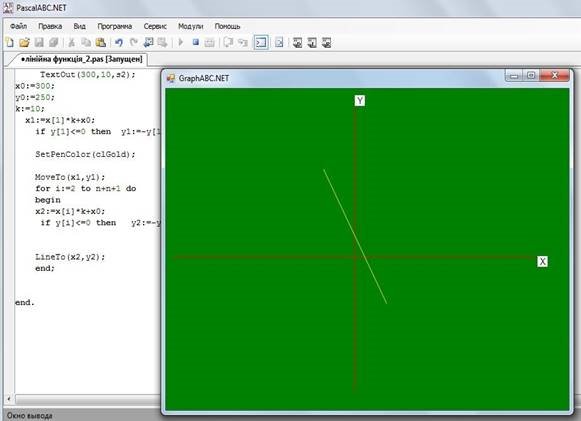
3 змінимо програму, щоб на екрані будувався графік лінійної функції (виду y=а-b*х)

 Додамо в опис змінні «a» та «b», надамо користувачу можливість задати їх значення, змінимо формулу, для обчислення значень функції.

      Програма має вигляд:

Program demo_func;

Uses GraphABC; 

 

var n,i,x0,y0,x1,y1,x2,y2,k,a,b:integer; s1,s2:string;

 

x,y:array[1..200] of integer;

 

Begin

Window.Clear(clGreen); 

writeln(' Програма для малювання графіка функції вигляду y=a-b*x ');

writeln(' введіть значення а= '); read(a); writeln(a);

writeln('введіть значення b= '); read(b); writeln(b);

writeln(' Програма малює графік функції вигляду y= ',a, '- ',b, '*x '); writeln(' введіть кількість значень змінної "x" = (програма визначить  значення  в діапазоні від -х до +х)');

 

read(n);

 

writeln('x= ',n);

 

x[1]:=-n; for i:=2 to n+n+1 do begin x[i]:=x[i-1]+1; end; 

 

 

for i:=1 to n+n+1 do begin

write('x[',i,']= ',x[i],'  '); end;  writeln;

writeln (' значення змінної y '); for i:=1 to n+n+1 do begin

y[i]:=a-b*x[i]; end; for i:=1 to n+n+1 do begin

write('y[',i,']= ',y[i],'  '); end; 

 Sleep(5000);

Window.Clear(clGreen); 

SetPenColor(clRed);

 

 MoveTo(10,250);

    LineTo(590,250); 

    

    MoveTo(300,10); LineTo(300,450);

    s1:=' X '; s2:=' Y ';

    TextOut(590,250,s1); TextOut(300,10,s2); x0:=300; y0:=250; k:=10; x1:=x[1]*k+x0;

    if y[1]<=0 then  y1:=-y[1]*k+y0 else y1:=-y[1]*k+y0;

   

    SetPenColor(clGold);

    

MoveTo(x1,y1);     for i:=2 to n+n+1 do     begin     x2:=x[i]*k+x0;

     if y[i]<=0 then   y2:=-y[i]*k+y0 else  y2:=-y[i]*k+y0;

    

   

LineTo(x2,y2);     end;   

 

end.

      Запустимо на виконання:

 

 

 

             

  

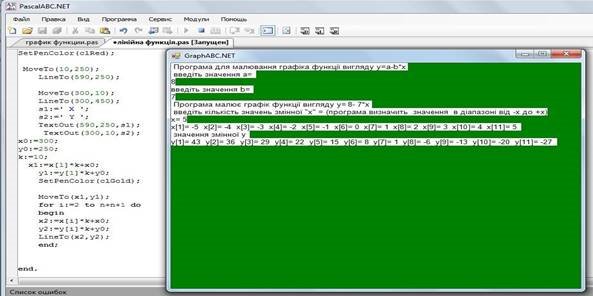
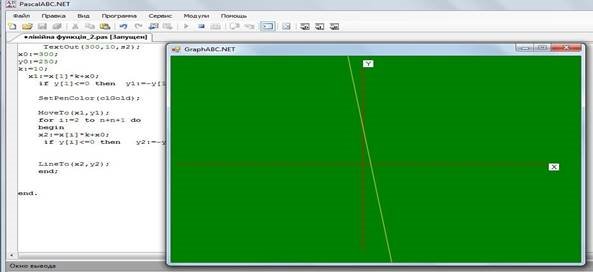
3.3 Обчислення відстані між двома точками

 

  writeln('обчислення відстані між двома точками A(x,y) та B(x,y)');    writeln('ввести номер першої точки');

read(xt);     writeln(xt);     write('значення х=  ');    writeln(x[xt]); write('значення y=  ');    writeln(y[xt]);    writeln('Ввести номер другої точки');    read(xm);     writeln(xm);    write('значення х=  '); writeln(x[xm]);     write('значення y=  ');    writeln(y[xm]);

   

ax:=x[xt];    ay:=y[xt];    bx:=x[xm];    by:=y[xm];

    

   

    

    

if ax>bx then    begin    AB:=sqrt((ax-bx)*(ax-bx) + (ay-by)*(ay-by)); writeln('відстань між двома точками ');    writeln(AB);    end    else begin

AB:=sqrt((bx-ax)*(bx-ax) + (by-ay)*(by-ay));    writeln('відстань між двома точками ');    writeln(AB);    end;

 

end.

 

 

 

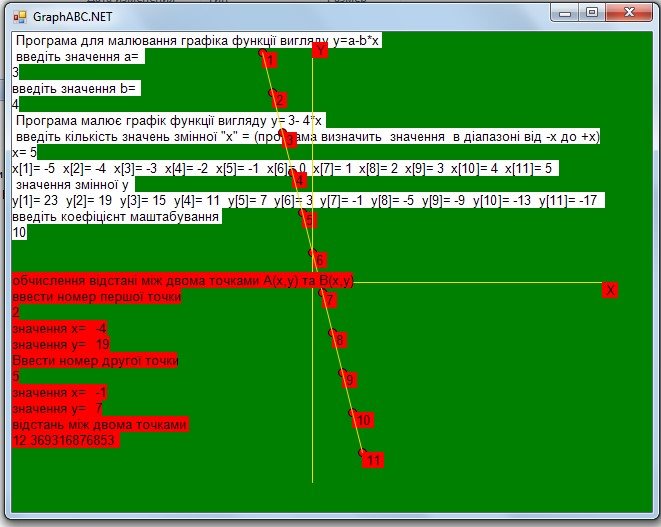
Висновки

•      Створену програму , яка за вказаними аргументами Х  знаходить  значення  лінійної функції  виду y=a-bx ,виводиться на екран набір значень X та Y;

•      Будується графік функції;

•      Значення які обчислюються в програмі співпадають з «обчисленими вручну» ;

•      В залежності від значень констант А та В змінюються вигляд графіку функції;

•      Кожне з значень на графіку помічено маркером (цифри 1,2,3…);

•      Програма надає можливість обчислити відстань між двома вказаними точками;

•      Представлена робота може використовуватись на уроках алгебри для кращого сприйняття матеріалу теми «лінійна функція та її графік». Проте програма має недоліки , які зумовлені можливостями мови програмування .

 

 

                 

Список використаних джерел

 

•      Аладьев В. З. Программирование и разработка приложений в Maple: монография / В. З. Аладьев, В. К. Бойко, Е. А. Ровба. - Гродно : ГрГУ; Таллинн : Межд. акад. Ноосферы, Балт. отд., 2007. – 458 с.

•      Аладьев В. З. Эффективная работа в Maple 6/7 / Аладьев В. З. – М. : Лаборатория Базовых Знаний, 2002. – 336 с.

•      Алєксєєв В. М. Математика. Довідковий повторювальний курс : навч. посібник / Алєксєєв В. М., Ушаков Р. П. ; за ред. М. Й. Ядренка. – К. : Вища шк., 1992. – 295 с.

•      Алексеев Е. Р. Решение задач вычислительной математики в пакетах Mathcad 12, MATLAB 7, Maple 9 / Алексеев Е. Р., Чеснокова О. В. – М. : НТ Пресс, 2006. – 496 с.

•      Бондаренко М. Ф. Математика для вступників до вузів : навч. посібник / М. Ф. Бондаренко, В. А. Дікарєв, О. Ф. Мельников та інші. – Харків : «Компанія СМІТ», 2002. – 1120 с.

•      Васильев А. Н. Maple 8. Самоучитель / Васильев А. Н. – М. : Издательский дом «Вильямс», 2003. – 353 с.

•      Гальперіна А. Р. Математика. Типові тестові завдання : збірник / • А. Р. Гальперіна, О. Я. Михєєва. – Х. : Веста, 2009. – 128 с. + Додат.

•      (16 с.). – (Серія журналу «Вісник ТІМО»).

•      Дьяконов В. П. Maple 7 : учебный курс / Дьяконов В. П. – СПб. : Питер, 2002. – 672 с.

•      Дьяконов В. П. Maple 9 в математике, физике и образовании / Дьяко-

•      нов В. П. – М. : СОЛОН-Пресс, 2004. – 688 с.

•      Егоров В. К. Сборник задач по математике для поступающих в вузы /

•      В. К. Егоров, В. В. Зайцев, Б. А. Кордомский ; под ред. М. И. Сканави. – М. : Высшая школа, 1992. – 528 с.

•      Кирсанов М. "Графы в Maple" / М. Кирсанов. – М. : Физматлит, 2007. – 168 с.

 

Список електронних джерел:

 

•      https://uk.wikipedia.org

•      http://mon.gov.ua/

•      http://osvita.ua  

 

 

                 

Додаток 1

 

 

 

 

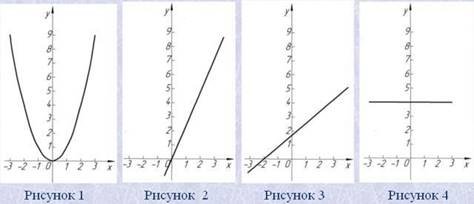
Додаток 2

 

 

 

 

 

 

 

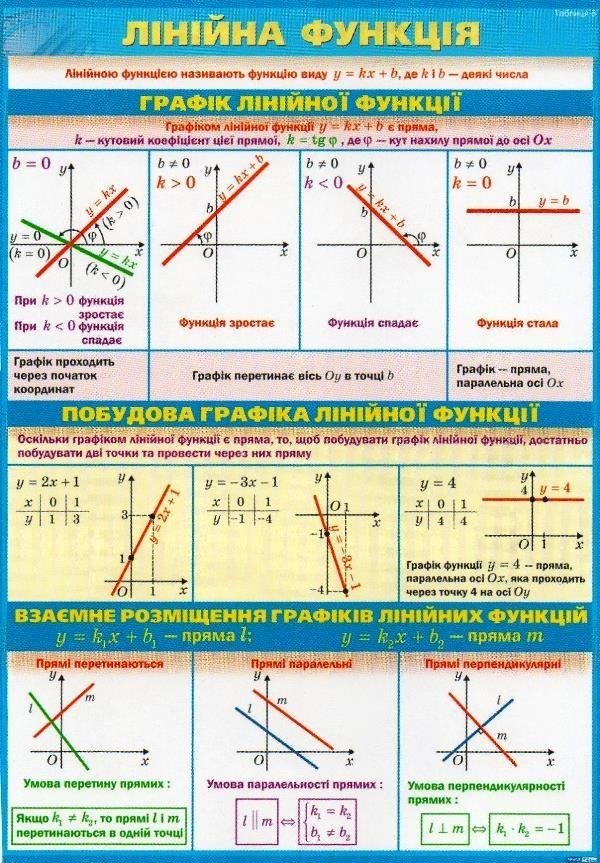
Додаток 3

Program demo_func;

Uses GraphABC; 

 

var n,i,x0,y0,x1,y1,x2,y2,k,a,b,yt,ym,xt,xm,ax,ay,bx,by:integer; AB:real; s1,s2:string; xn,yn,x,y:array[1..200] of integer; si:array[1..200] of string; Begin

Window.Clear(clGreen);

si[1]:=' 1 '; si[2]:=' 2 '; si[3]:=' 3 '; si[4]:=' 4 '; si[5]:=' 5 '; si[6]:=' 6 '; si[7]:=' 7 '; si[8]:=' 8 '; si[9]:=' 9 '; si[10]:=' 10 '; si[11]:=' 11 ';

writeln(' Програма для малювання графіка функції вигляду y=a-b*x '); writeln(' введіть значення а= '); read(a); writeln(a); writeln('введіть значення b= '); read(b); writeln(b); writeln(' Програма малює графік функції вигляду y= ',a, '- ',b, '*x '); writeln(' введіть кількість значень змінної "x" = (програма визначить  значення  в діапазоні від -х до

+х)'); read(n); writeln('x= ',n); x[1]:=-n; for i:=2 to n+n+1 do begin x[i]:=x[i-1]+1; end;  for i:=1 to n+n+1 do begin

write('x[',i,']= ',x[i],' '); end;  writeln; writeln (' значення змінної y '); for i:=1 to n+n+1 do begin y[i]:=a-b*x[i]; end; for i:=1 to n+n+1 do begin

write('y[',i,']= ',y[i],' '); end;   Sleep(5000);  x0:=300; y0:=250; k:=10;  for i:=1 to n+n+1 do begin xn[i]:=x[i]*k+x0;

if y[i]<=0 then  yn[i]:=-y[i]*k+y0 else yn[i]:=-y[i]*k+y0; end; writeln; writeln (' значення змінної x '); for i:=1 to n+n+1 do begin

write('xn[',i,']= ',xn[i],' '); end;  writeln; writeln (' значення змінної y '); for i:=1 to n+n+1 do begin

write('yn[',i,']= ',yn[i],' '); end;  brush.Color:=clRed; for i:=1 to n+n+1 do     begin circle(xn[i],yn[i],4);         TextOut(xn[i],yn[i],si[i]);    end;

SetPenColor(clGold);

MoveTo(xn[1],yn[1]);

LineTo(xn[n+n+1],yn[n+n+1]);

MoveTo(10,250);

LineTo(590,250); 

    

MoveTo(300,10);      LineTo(300,450);

s1:=' X ';     s2:=' Y ';     TextOut(590,250,s1);      TextOut(300,10,s2);

writeln;

writeln('обчислення відстані між двома точками A(x,y) та B(x,y)'); writeln('ввести номер першої точки');

read(xt);     writeln(xt);     write('значення х=  ');    writeln(x[xt]); write('значення y=  ');    writeln(y[xt]);    writeln('Ввести номер другої точки');    read(xm);     writeln(xm);    write('значення х=  '); writeln(x[xm]);     write('значення y=  ');    writeln(y[xm]);

   

ax:=x[xt];    ay:=y[xt];    bx:=x[xm];    by:=y[xm];

    

   

    

    

if ax>bx then    begin

AB:=sqrt((ax-bx)*(ax-bx) + (ay-by)*(ay-by));

writeln('відстань між двома точками ');    writeln(AB);    end    else begin

   AB:=sqrt((bx-ax)*(bx-ax) + (by-ay)*(by-ay));    writeln('відстань між двома точками '); writeln(AB);    end;

 

end.