Математичний вечір "Історія чисел"

Загальноосвітня школа І-ІІІ ступенів с.Велика Яблунька

 

 

 

 

  

      Історія чисел

              Математичний вечір

 

 

 

 

 

 

                                      

                                   

                                         Вчитель Радчук Т.С.

 

 

 

 

                                         2020

 

Мета:

• продовжувати ознайомлювати учнів з історією виникнення чисел, римськими, арабськими числами, позиційною системою числення;

• розвивати логічне мислення, розумову активність, пізнавальний інтерес;

• виховувати любов до математики, зібраність, комунікативність, ініціативність.

 

Обладнання: комп’ютер, мультимедійний проектор, малюнки, рахівниця.

                               Розповідати про сучасну

                               математику без посилання на математику

                               минулого – це те саме, що грати третій

                               акт п’єси, не пояснивши попередньо, що

                               відбувалося в перших двох.

                                                                        У. Сойєр

                                    

                                              Хід заходу

І. Організаційний момент

ІІ. Вступне слово вчителя

  Дорогі друзі! Рада вітати вас усіх на математичному вечорі «Історія чисел». Ця тема хвилювала людство і математиків різних епох. Зверніть увагу на епіграф, підібраний  до свята. Як влучно і доречно підходять слова У.Сойєра до теми про історію розвитку і становлення поняття про число.

  Учні 5 класу підготували цікаві факти про різні числа і презентацію до виступу, яку будуть коментувати по ходу виступу.

   Діти, мистецтво лічби розвивалося разом із людством. За тих часів, коли людина лише збирала в лісі плоди й полювала, їй для рахунку вистачало чотирьох слів: один, два, три і багато. Саме так лічать і нині деякі племена, що живуть у джунглях Південної Америки.

  Проте, коли люди почали займатися тваринництвом і землеробством, в них уже виникла потреба лічити кіз у стаді чи кількість корзин з вирощеними плодами (яких було більше трьох), заготовленими на зиму.

Способів лічби було придумано немало: робилися зарубки на палиці за кількістю предметів, зав’язувалися вузли на мотузці, складалися в купу камінці.  Але ж палицю з собою не візьмеш, та й каміння тягати не дуже приємно, а пастухові треба знати, чи не відбилася якась коза від стада. І тут на допомогу приходять пальці рук – чудовий рахунковий матеріал, ним досі послуговуються не лише першокласники. А коли предметів більше десяти? Звісно, можна використовувати пальці на ногах. А далі? Тут уже не було іншої ради, як винайти десяткову систему, якою ми послуговуємося й нині: рахуємо десятки; коли набереться десять десятків, називаємо їх сотнею; потім десять сотень – тисячею. У Київській Русі десять тисяч називали «тьмою». Звідси вислів «тьма люду».

Ведучий 1

  «Пальцеве» походження десяткової системи підтверджується формою латинських цифр: римська цифра п’ять (V) – долоня з відігнутим великим пальцем, а римське десять (X) – дві руки навхрест.

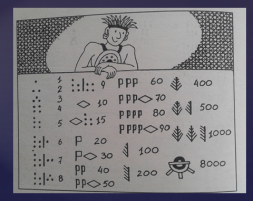
  Подивіться на таблиці: так рахували індіанці племені майя в Америці, предки європейців.

  Деяким племенам служили лише чотири пальці однієї руки, одначе при цьому враховувалося, що кожен палець складається з трьох фаланг, тобто в розпорядженні було дванадцять об’єктів лічби. Так виникла дюжина, яка більше ста років тому була дуже поширена в Європі, та помалу поступилася десятці. Досі в Європі на дюжини лічать ґудзики, носовички, курячі яйця та багато іншого, що продається поштучно.

Ведучий 2

А чи знаєте ви як називається дванадцять дюжин ( це 144 одиниці)? (Грос)

А які великі числа, більші за мільярд (або більйон, «бі» латиною – два) можете назвати? (1 000 000 000 000 – трильйон, далі 1 000 000 000 000 000 – квадрильйон, далі квінтильйон, секстильйон, септильйон, октильйон, нонильйон, децильйон). Кожна наступна одиниця містить тисячу попередніх.

 Ведучий 1

 Проте великі числа в повсякденному житті не потрібні.

Вони постають, скажімо, в астрономії, тому нерідко кажуть про «астрономічні числа», бо маси зірок і відстані між ними складають справді великі числа.

Ведучий 2

Однак фізики підрахували, що кількість атомів –найдрібніших часток речовини –у всьому Всесвіті не перевищує числа, що позначається одиницею зі ста нулями.

Яку назву дістало це число? (Гугол)

ІІІ.Повідомлення учнів

1. Числа 1,2,3,…,які використовують для лічби предметів назвали натуральними. Проте ремісникам і торговцям цих чисел було замало, оскільки виникла необхідність ділити на частини землю, спадщину і багато чого іншого. Так з’явилися дроби та правила обчислення їх і використання в практиці.
2. Тепер торговцям і ремісникам чисел вистачало. Але ще математики Стародавньої Греції, учні славетного Піфагора, виявили, що є числа, які не передаються жодним дробом (наприклад, довжина діагоналі квадрата зі стороною 1). Ці числа назвали ірраціональними ( першим є √2) – недосяжними для розуміння, а цілі числа й дроби – раціональними.
3. На цьому історія числа не закінчилася. Математики ввели в ужиток від’ємні числа, які виявилися вельми зручними для розв’язування багатьох задач.
4. Хто із вас скаже де вперше почали використовувати від’ємні числа і коли? (В Китаї, ІІ ст. до нашої ери)

Учитель. Діти, а скільки в математиці є цифр? (Десять: 1,2,3,4,5,6,7,8,9,0 ) Ці цифри називають арабськими, хоча араби лише передали до Європи розроблений індусами спосіб запису чисел. Про це пише один з перших математиків доби Відродження Леонардо Пізанський, який дістав прізвисько Фібоначчі.

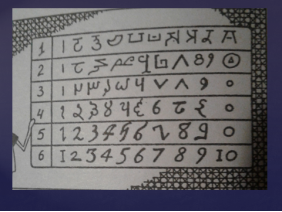
  Подивіться на таблицю розвитку позначення цифр.

Араби вибрали з цих різних видів цифр найбільш вдалі. Від них цифри проклали свій шлях по планеті.

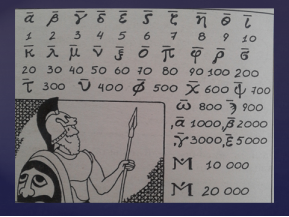
  У Стародавній Греції вчинили дуже просто: греки не стали придумувати спеціальне написання цифр, а використовували літери. (Див.  таблицю). Над літерами ставили рисочку. В Київську Русь також прийшла ця система запису, але замість рисочки ставили хвилясту лінію – титло. ( Див. таблицю)

5. Справді дивовижні математики Стародавньої Греції і викликають мимовільний захват. Проте одного відкриття давні греки не зробили. Якого? (Не придумали нуля).

  Нам легко з висоти багатовікового досвіду людства знизувати плечима: чого ж бо ви, греки і римляни, таку просту річ, як нуль, не дотумкали?

6. А це було аж ніяк не просто. Що таке «нічого»? Порожнє місце! Якщо нічого немає, кому спаде на думку щось писати, коли можна не писати нічого!

  Хто першим здогадався позначати цифрою «ніщо». Ми ніколи не дізнаємось цього. Можемо лишень твердити, що таких геніїв було кілька. І хтось вигадав знак для нуля в Давньому Вавилоні. Хтось із індіанців майя – в Америці. Хтось –  у Китаї. І хтось із мудреців Індостану позначив порожнє місце тим самим кружечком, яким увесь світ послуговується донині. (Таблиця)

7. Тепер будь-яке число можна було занотовувати, користуючись тими самими цифрами. І вже не сплутаєш 12 зі 120 або 102. З’явилася позиційна система числення, в якій значення цифри залежить від її місця в числі – позиції. А користуватись нею дуже легко.

  Учитель. А зараз ми поговоримо про числа, яким дали особливі назви.

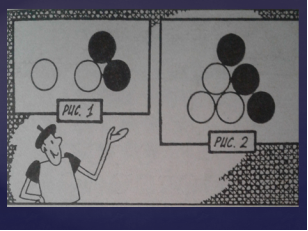
Фігурні числа. Сивої давнини, допомагаючи собі при рахуванні камінцями, люди зауважували правильні фігури, які можна викласти з камінців. Можна просто класти камінці вряд: один, два, три…А що коли складати трикутник? У нас вийде така послідовність чисел: 1, 1+2=3, 1+2+3=6, 1+2+3+4=10 і т.д.

  Числа 1,3,6,10,15,21,28,36, … називають «трикутними».

 

  Вельми цікавими є квадратні числа, тобто такі, що утворюють при викладанні із камінців квадратів. Ось вони:1,4,9,16,25,36,49,64,81,100…

  Також цікавими є кубічні числа, що виникають при складанні кубиків: 2∙2∙2=8; 3∙3∙3=27; 4∙4∙4=64 іт.д.

Ведучий 1 А які числа називаються простими? (Ті, що мають два дільники: саме число та одиницю). Це вам відомо. А хто знає, що таке досконалі числа?

Візьмемо, наприклад, число 6. Випишемо його дільники, відмінні від самого числа і додамо їх (1+2+3=6). Чи є ще такі числа? Ось число 28. Перевірте, що

28=1+2+4+7+14. А ще? Є й ще.

496=1+2+4+8+16+31+62+124+248

  Числа, що дорівнюють сумі всіх своїх дільників (за винятком самого числа), давньогрецькі математики називали досконалими.

  Ведучий 2 Ці числа досі залишаються загадкою для математиків. По-перше, всі відомі досконалі числа є парними, і невідомо, чи можуть існувати непарні досконалі числа. По-друге, хоча й знайдено вже кілька десятків досконалих чисел, однак невідомо, скінченна їх кількість чи нескінченна. Про парні досконалі числа вже було відомо Евклідові.

  Ведучий 1 А чи чули ви щось про дружні числа? Піфагор говорив:

«Мій друг той, хто є моїм другим я, як числа 220 та 284».

Ці два числа прикметні тим, що сума дільників кожного з них дорівнює другому числу. Справді, 1+2+4+5+10+11+20+22+40+44+55+110=284, а 1+2+4+71+142=220

Вчитель. Ви почули багато цікавих фактів про числа і їх виникнення. А зараз пропонуємо вашій увазі вікторину.

ІV. Вікторина

1. Скільки дільників має число 24? Назвати їх. (Вісім: 1, 2, 3, 4, 6, 8, 12, 24)
2. Назвати прості числа-близнюки (наприклад 11 і 13;17 і 19).
3. Назвати найменше натуральне число (1).
4. Чи існує просте парне число? (Існує, 2).
5. Записати число 95 римським числом (VC).
6. Назвати найбільше натуральне шестицифрове число (999999).
7. Запиши арабськими число XLIV (44).
8. Піднести швидко усно 85 до квадрата (8·(8+1)=8·9=72 – перша частина відповіді; дописуємо справа25 – другу частину відповіді -7225)
9. Підберіть корінь рівняння m: m= m· m (1).
10.                  На яке число треба помножити 259259, щоб одержати добуток, який записується тільки цифрами 7? (на 3)
11.                  Як записують в Китаї слова і числа? (Ієрогліфами)
12.                  Назвати усі двоцифрові числа, у кожного з яких сума цифр дорівнює 2 (11; 20).
13.                  Яке найбільше число можна скласти з цифр 1, 0, 3, 6, 8, використовуючи кожну із цифр лише по одному разу? (86310)
14.                  Яке число є коренем рівняння х-х=х·х? (0)
15.                  Назвати найбільше натуральне число (немає).

IV. Приклади нестандартного множення чисел

Ведучі показують приклади множення чисел: 567· 3984; 124·608  ( за Лукою Пачіолі).

V. Перегляд виставки дитячих робіт (у формі чисел).

 

 

 

 

 

 

Література

 

1. Арістов В.І. Усний рахунок – інтелектуальний вид спорту. Киів:Видавництво Європ. Ін-ту, 2008.
2. Газета .Математика. №18, 2018.
3. Дитяча енциклопедія. Я пізнаю світ. Киів. Видавництво «Школа», 2002. Київ. Генеза, 2018
4. О.С.Істер. Математика. 5 клас.

 

 

 

Слайди до презентації