Медодична розробка уроку.

Тема уроку: правильні многогранники.

Мета уроку: формувати поняття правильних многогранників: правильний тетраедр, куб, октаедр, додекаедр, ікосаедр. Розвинути вміння знаходити подібні та відмінні ознаки у розглянутих правильних многогранниках. Виховання вмінь знаходити у навколишньому середовищі та побуті тіла даних геометричних форм, встановлювати між ними причино-наслідкові зв’язки.

Обладнання: моделі правильних многогранників, персональний комп'ютер з

                          створеною презентацією, плакат, роздатковий матеріал (картки

                         з математичним диктантом), підручник Математика  11.

Г.П. БЕВЗ, В.Г. БЕВЗ

 Тип уроку: урок засвоєння нових знань.

Міжпредметні зв'язки: інформатика - програма Роwег Роіnt,

ХІД УРОКУ      І.Організаційна частина.

• Перевірка присутніх учнів
• Перевірка готовності до уроку.

II. Перевірка домашнього завдання.

Учні отримують по два листки (Додаток 1).

Математичний диктант

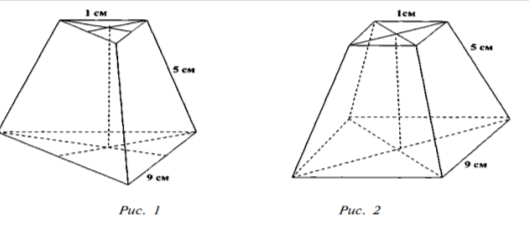
Дано правильну зрізану піраміду, бічне ребро якої дорівнює 5 см, а в основах лежать:

варіант І - трикутники (рис. 1);

варіант II - квадрати (рис. 2) зі сторонами 1 см і 9 см.

Знайдіть:

а) апофему зрізаної піраміди; (3 бали)

б) площу бічної грані; (3 бали)

в) площу бічної поверхні зрізаної піраміди; (3 бали)

г) площу меншої основи (3 бали)

 Відповідь. 

Варіант І а) 3 см; б) 15 см² ;     в) 45 см² ; г) см² .

Варіант II а) 3 см; б) 15 см ; в) 60см² ; г) 1 см² .

Після виконання завдань математичного диктанту, перший листок учні здають на перевірку викладачу, а відповіді на другому - самостійно звіряють з правильними, що з'являються на екрані монітора.

Таким чином, учні вчаться роботи самооцінку знань.

III. Повідомлення теми, мети і плану уроку. Мотивація навчальної діяльності учнів.

У курсі планіметрії ви познайомилися з правильними многокутниками.

- Які многокутники називаються правильними?

- Многокутник називається правильним, якщо у нього всі сторони і
всі кути рівні.

Існує безліч правильних многокутників. Давайте пригадаємо:

- За якою формулою знаходиться площа правильного трикутника зі
стороною а?

S=

- А за якою формулою обчислюється площа квадрата зі стороною а?

S = а²

По аналогії до планіметрії в стереометрії існують правильні многогранники, види яких ми сьогодні вивчатимемо.

Випереджувальне завдання (Історична довідка)

Доведення існування п'яти видів правильних многогранників приписують Піфагору, який називав їх „космічними фігурами". Властивості правильних многогранників докладно дослідили піфагорійці у VI ст. до н. є.

Як свідчать дослідження німецького математика Ф. Ліндемана, усі п'ять видів правильних многогранників були відомі і стародавнім єгиптянам.

Отже, записуємо тему сьогоднішнього уроку:

Правильні многогранники.

Девізом нашого уроку будуть такі слова:

„Математика здає свої фортеці лише сильним, сміливим і
кмітливим" А. Конфорович

Сьогодні на уроці ми будемо працювати згідно такого плану:

План уроку

1.   Типи правильних многогранників та їх властивості.
2.   Розв'язування задач.

IV. Сприйняття та усвідомлення нового матеріалу.

1. Типи правильних многогранників та їх властивості.

Означення. Опуклий многогранник називається правильним, якщо його грані є правильними многокутниками з однією і тією ж самою кількістю сторін, а в кожній вершині многогранника сходиться одне і те ж число ребер. Існує п'ять типів правильних опуклих многогранників:

 - правильний тетраедр,

 - правильний гексаедр (куб),

 - правильний октаедр,

 - правильний додекаедр,

  - правильний ікосаедр.

Назва многогранників складається із двох частин: перша - число граней (тетра - 4, гекса - 6, окта - 8, до дека - 12, ікоса - 20), а друга (едр) -грань.

Демонструються моделі правильних многогранників. Далі розглядається кожний тип правильних многогранників і заповнюється наступна таблиця.

Випереджувальне завдання

(Приклади правильних многогранників в природі)

Правильні многогранники трапляються в природі. Так, наприклад кристали кухонної солі мають форму куба, кристалічна сірка має форму октаедра, кристали пірита мають форму, близьку до правильного додекаедра. За дослідженнями англійського вченого Дж. Бернала групи молекул рідини мають форму правильного додекаедра, що забезпечує рідині вільний рух.

2. Розв'зування задач.

Колективне розв'язування задач: 1. Визначити суму плоских кутів при вершині кожного із п'яти видів правильних многогранників:

2. Поверхня додекаедра рівна 180 см². Визначити площу його грані.

(180: 12=15(см²))

3. Обчисліть повну поверхню правильного тетраедра, якщо радіус кола,
описаного навколо його грані, дорівнює R.

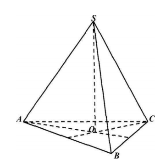Розв'язання

Оскільки SАВС — правильний тетраедр, то всі його ребра рівні, а всі грані є правильними трикутниками. Нехай R - радіус кола, описаного навколо ∆АВС;

К = ОА - за умовою.

АВ = R  (за      властивістю правильного трикутника).

Оскільки ∆АВС - правильний, то

S∆АВС=

Sп=4S∆АВС; Sп=4

Відповідь. 3R²

4. Який існує зв'язок між поняттями: правильна трикутна піраміда і правильний тетраедр?

(Правильний тетраедр є частковий випадок правильної піраміди).

V. Підведення підсумку уроку.

Завдання    для    учнів:

1. Які многогранники називаються правильними?
2. Скільки існує типів правильних многогранників?
3. Знайдіть площу поверхні правильного:

а) тетраедра;

б) гексаедра (куба);

в) октаедра;

г) ікосаедра.

якщо його ребро дорівнює а.

Відповідь.  а) а;  б) 6а² ;  в) 2а ;  г) 5а²

VI. Домашнє завдання.