Метод безпосереднього використання законів Кірхгофа для розв'язування задач з теми "Ланцюги постійного струму"

Олеярник Олександр Вікторович – вчитель фізики та астрономії загальноосвітньої школи № 33, Краматорської міської ради, Донецької області

Мета роботи: показати розв’язування ланцюгів постійного струму використовуючи закони Кірхгофа, навчити учнів визначати значення опорів та покази електровимірювальних приладів, розвивати логічне та алгоритмічне мислення при вирішуванні задач, зацікавати предметом фізики та дослідницьким процесом, виховувати спостережливість та уважність

 Метод безпосереднього використання законів Кірхгофа для розв’язування задач з теми «Ланцюги постійного струму»

Мета:

Навчальна: навчити учнів розв’язувати ланцюги постійного струму методом безпосереднього використання законів Кірхгофа на прикладі задач середнього рівня важкості, вміти знаходити значення вимірювальних приладів;

Розвивальна:розвивати логічне та алгоритмічне мислення в учнів, вміння вирішувати задачі, формувати навички самостійної роботи, розширювати кругозір;

Виховна: викликати зацікавленість до розв’язування задач, виховувати культуру мовлення, привчати до уваги, сформувати допитливість, уміння робити висновки

Розглянемо, як можна використовуючи метод безпосереднього використання законів Кірхгофа визначати струм, опір, напругу, значення вимірювальних приладів, на прикладі наступних задач.

Задача 1

Напруга, яка прикладена до ланцюга, U = 12 (В); потужність що вимірюється ватметром, Р = 10 (Вт). Значення опорів проставлені на

рисунку 1. Визначте величину опору R_X?

Рисунок 1 – Схема електричного ланцюга

Розв’язання

Ватметр W вимірює потужність ділянки ланцюга між вузлами а та d. Опори R₁, R₂ та опір R₃ з’єднані паралельно. Точки а та с мають однаковий потенціал, оскільки з’єднані дротом, про опір якого нічого не сказано. Точка b є загальною. Тому має з’єднання, при якому зажими різних гілок мають однакові потенціали, що є  признаком паралельного з’єднання. Тому:

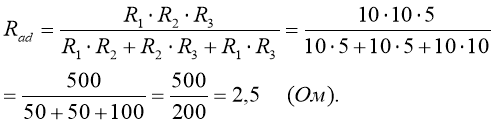
Можна обчислити R_ad :

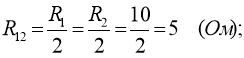
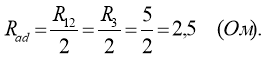
З співвідношення для потужності         визначимо струм I:

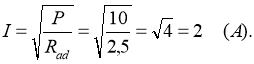
Складемо рівняння за 2-м законом Кірхгофа для еквівалентного ланцюга (рис. 2), обрав напрям обходу за годинниковою стрілкою:

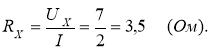
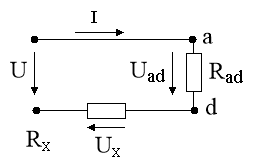
Рисунок 2 – Схема еквівалентного ланцюга

Відповідь: R_X = 3,5 (Ом).

Задача 2

Яким повинен бути опір R_X (рис.3), щоб при замиканні ключа К струми в ланцюзі не змінювались? Задано: R₁ = 6 (Ом), R₂ = 3 (Ом), R₃ = 8 (Ом),

R₄ = 1 (Ом), Е₁ = 20 (В), Е₂ = 25 (В), Е₃ = 30(В), Е₄ = 45 (В).

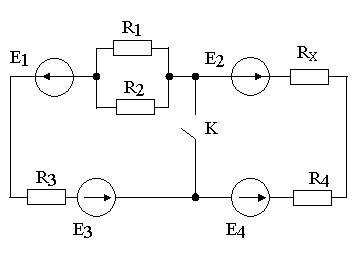
Рисунок 3 – Схема ланцюга до задачі 2

Розв’язання

Розглянемо схему у початковий момент часу, коли ключ К разімкнуто. Обрав довільно напрям обходу, наприклад проти руху годинникової стрілки, складемо рівняння за 2-м закон Кірхгофа для зовнішнього контура:

де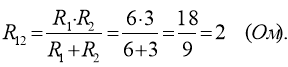

Після замикання ключа К, за умовою задачі, струм у кожному контурі повинен залишитись незмінним. Визначимо струм I для контуру з эдс Е₁ та Е₃ при замкненому ключі К:

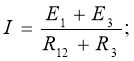
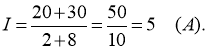
З рівняння (*) можна знайти опір R_X:

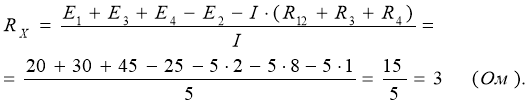
Відповідь: R_X = 3 (Ом).

Задача 3

Визначити напругу U_ab для заданих ланцюгів (рис.4)

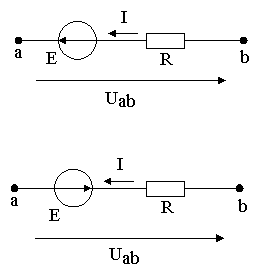
Рисунок 4 – Схеми електричних ланцюгів до задачі 3: з ЕРС Е, що співпадає зі струмом I за напрямом (а), та ЕрС Е, спрямовану зустрічно струму I (б)

Розв’язання

Вираз для напруги U_ab отримаємо з рівнянь, складених за 2-м законом Кірхгофа для заданих ланцюгів. Контури, вздовж яких проводиться обхід, можуть замикатися не тільки за гідками ланцюга, але й за векторами напруг. Для обох ланцюгів оберемо напрям обходу за годинниковою стрілкою.

Для першого ланцюга (рис.4,а):

Для другого ланцюга (рис.4,б):

Визначимо напругу U_cb, якщо U_аb = 5 (В), Е = 5(В), R₁ = 1 (Ом),

R₂ = 2 (Ом) (рис.5).

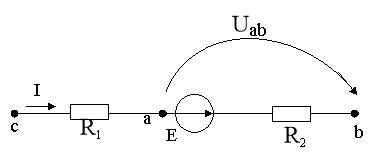
Рисунок 5 – Схема електричного ланцюга до задачі 3

Розв’язання

Значення напруги U_ab відомо, тому для визначення напруги U_сb необхідно знайти напругу на резисторі R₁.

З рівняння, складеного за 2-м законом Кірхгофа для ділянки ланцюга ab, визначимо струм I:

Звідси:

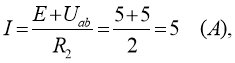
Напруга

Відповідь: