Методичні матеріали до заняття на тему: "Розв’язування задач на знаходження площ поверхонь тіл обертання "

Про матеріал

План-конспект заняття з математики (геометрія) . Тема: «Розв'язування задач на знаходження площ поверхонь тіл обертання». Мета: формувати навички та вміння студентів знаходити площі поверхонь тіл обертання; застосовувати набуті знання при розв'язуванні задач; виробляти навички практичного застосування властивостей тіл обертання та формул для обчислення площ поверхонь; розвивати просторову уяву, логічне мислення, творчі здібності, увагу і пам'ять; стимулювати пізнавальну діяльність. Дані методичні матеріали використовуються при вивченні теми «Тіла обертання», дозволяють організувати викладачу пізнавально-навчальну діяльність студента на занятті.

Перегляд файлу

ПЛАН ЗАНЯТТЯ

Тема заняття: Розв’язування задач на знаходження площ поверхонь тіл обертання .

Мета заняття:

навчальна: формувати навички та вміння студентів знаходити площі поверхонь тіл обертання; застосовувати набуті знання на практиці; формувати вміння швидко і чітко формулювати власні думки;

розвиваюча: розвивати вміння і навички застосовувати набуті знання при розв’язуванні задач; виробляти навички практичного застосування властивостей тіл обертання та формул для обчислення площ поверхонь; розвивати просторову уяву, логічне мислення, творчі здібності, увагу і пам’ять; стимулювати пізнавальну діяльність;

виховна: виховувати інтерес до математики, культуру усного мовлення, культуру математичних записів, наполегливість, самостійність, працьовитість, прищеплювати бажання мати якісні, глибокі знання з предмету;

методична: ознайомлення з методикою організації формування вмінь та навиків при розв’язуванні задач.

Обладнання: мультимедійне обладнання, ноутбук, електронний супровід (презентація), стереометричні моделі, роздатковий матеріал, креслярські прилади.

Форма проведення заняття: класно – урочна.

Тип заняття: формування вмінь та навиків застосовувати теоретичний матеріал при розв’язуванні задач.

Основна література:

Погорєлов О.В. Геометрія: Стереометрія Підруч. для 10-11 кл. серед . шк. - К.: Школяр, 2007.
Математика: 11кл.: підр. для заг. навч. закл.: рівень стандарту / Г.П. Бевз, В.Г. Бевз.- К.: Генеза, 2011.

ЗМІСТ І ХІД ЗАНЯТТЯ

№ елементу заняття

Елементи заняття, питання, форми, методи навчання та засоби забезпечення заняття

І.

Організаційна частина

Перевірка присутності студентів та їх підготовки до заняття.
Перевірка санітарного стану кабінету.

Привітання.

Ось дзвінок нам дав сигнал.

Працювати час настав.

Тому сіли всі рівненько, посміхнулися гарненько.

Настрій гарний узяли, працювати почали.

Сьогодні на занятті ми будемо не тільки працювати, а ще й здійснювати самоконтроль. Кожен з вас на кожному етапі заняття може отримати бали, які ви будете заносити в картку самоконтролю. В кінці заняття підсумуємо бали для оцінювання.

Роботу організуємо на довірі, оскільки знання ви здобуваєте для себе і тому девізом заняття буде відоме українське прислів’я:

«Знання збираються по краплині, як вода в долині»

ІІ.

Актуалізація опорних знань

Перевірка наявності домашнього завдання.
Бліц - опитування «Метеоритний дощ».

Які ви знаєте тіла обертання?
Яке тіло утвориться в результаті обертання прямокутника навколо сторони як осі?
Яке тіло утвориться в результаті обертання прямокутного трикутника навколо катета як осі?
Яке тіло утвориться в результаті обертання круга навколо його діаметра?
Яке з тіл обертання має вершину?
Який вчений вважав кулю найдосконалішою з усіх геометричних тіл?
Яка фігура є осьовим перерізом циліндра ?
Якою фігурою є осьовий переріз конуса?
Як називають поверхню кулі?
Якою фігурою є переріз кулі площиною?
Що таке великий круг?

Пригадаємо, основні елементи тіл обертання.

Як називається пряма, яка проходить через центри основ циліндра?
Як називаються радіуси основ циліндра?
Як називається відрізок, який сполучає відповідні точки на колах основ циліндра?
Що називається висотою циліндра?

Як називається найвища точка конуса?
Як називається перпендикуляр, опущений з вершини конуса на площину основи?
Що таке радіус кулі?

Пригадаємо формули для обчислення площ поверхонь тіл обертання.

Розглянемо циліндр.

- S = πR² .

Що обчислимо за цією формулою?

- S_б= 2π R H.

Що обчислимо за цією формулою?

- За допомогою формули S_п= S_б₊2 S_о обчислюють…

Розглянемо конус.

- S = πR² . Що обчислимо за цією формулою?

- S_б= π R L . Що обчислимо за цією формулою?

Розглянемо кулю.

- Назвіть формулу, за якою обчислюють довжину кола.

- За якою формулою обчислюють площу поверхні кулі?

Творче пошукове завдання (перегляд презентацій).

На минулому занятті вам було запропоновано створити презентацію, присвячену певному тілу обертання. Вашим завданням було презентувати одне з тіл обертання та навести приклади, де зустрічаються тіла обертання в повсякденному житті.

Тож нехай на цьому етапі заняття вашим девізом стануть слова “Тільки в спільній праці народжується істина“.

Я переконалася, що ви маєте міцні знання з теми «Тіла обертання». Знаєте елементи тіл обертання, знаєте формули для обчислення площ поверхонь тіл обертання. Перевіримо чи вмієте ви застосовувати набуті знання при розв’язуванні задач.

ІІІ.

Мотивація навчальної діяльності студентів

Незабаром – ЗНО. І тому ви маєте систематизувати свої знання з теми «Тіла обертання». Вміти розпізнавати тіла обертання, розуміти спосіб їх утворення та вміти обчислювати площі поверхонь при розв’язуванні стереометричних та прикладних задач.

Тіла обертання широко використовуються в техніці. Наприклад, кулі використовують при перемиканні передач, у клапанних пристроях. У формі циліндра виготовлені найважливіші складові частини автомобілів: генератор, конденсатор, фільтр тощо. Форму тіл обертання мають багато деталей і вузлів машин та механізмів. Тому в житті і трудовій діяльності ви, безперечно, матимете справу з тілами обертання.

ІV.

Оголошення теми, мети та плану заняття

Тема. Розв’язування задач на знаходження площ поверхонь тіл обертання .

План

Задачі за готовими рисунками.
Розв’язування прикладних задач.
Практична робота.

Формування вмінь і навичок обчислювати площі поверхонь тіл обертання

Розв’язування задач за готовими рисунками (наприклад).

Задача 1.

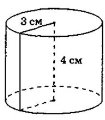
Визначте, які з наведених тверджень є правильними, а які – неправильними.

а) Довжина кола основи циліндра дорівнює 6π см.

б) Площа основи циліндра дорівнює 6π см .

в) Площа бічної поверхні циліндра дорівнює 2 π см .

Задача 2.

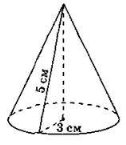
$G:\KOLEDZ\Статті_\Фінанси\image2314_2.jpg$

Визначте, які з наведених тверджень є правильними, а які – неправильними.

а) Площа повної поверхні конуса дорівнює 24 π см.

б) Площа основи конуса дорівнює 9π см.

в) Площа бічної поверхні конуса дорівнює 12 π см.

Розв’язування прикладних задач.

1). Циліндричний паровий котел з кришкою має діаметр 2м і висоту 10м. Скільки кв. метрів листової сталі пішло на його виготовлення, якщо на шви додається 10% всієї поверхні циліндра.

2). Конусоподібний намет висотою 3,5 м і діаметром основи 4 м покрито тканиною. Скільки тканини пішло на намет? Якби у наметі треба було шити і підлогу, то скільки матеріалу пішло б на неї?

3. Задача для кмітливих.

Задача Леонардо да Вінчі (італійський художник, скульптор, займався наукою та інженерною справою).

№ 1366. Площа основи якого циліндра дорівнює площі його бічної поверхні.

VІ.

Закріплення матеріалу.

Розглянемо практичне застосування формул для обчислення площ поверхонь тіл обертання.

Кожний студент отримує стереометричну модель одного з тіл обертання. Вимірює та знаходить відповідні елементи. За цими даними обчислює бічну та повну поверхні тіла.

2. Група ділиться на три команди. Кожній видається модель головного убору. Треба зробити виміри і скласти задачу з поставленим запитанням (Скільки матерії потрібно для пошиття капелюха?)

VІІ.

Узагальнення та систематизація знань

Інтерактивна гра «Вірю, не вірю».

VІІІ.

Підведення підсумків. Мотивація та виставлення балів.