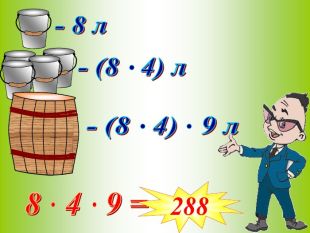
"Множення натуральних чисел"

Множення натуральних чисел та його властивості Підготувала Рашуга Наталя Іванівна Світ, що нас оточує – це світ математики. Тож давайте його пізнавати.

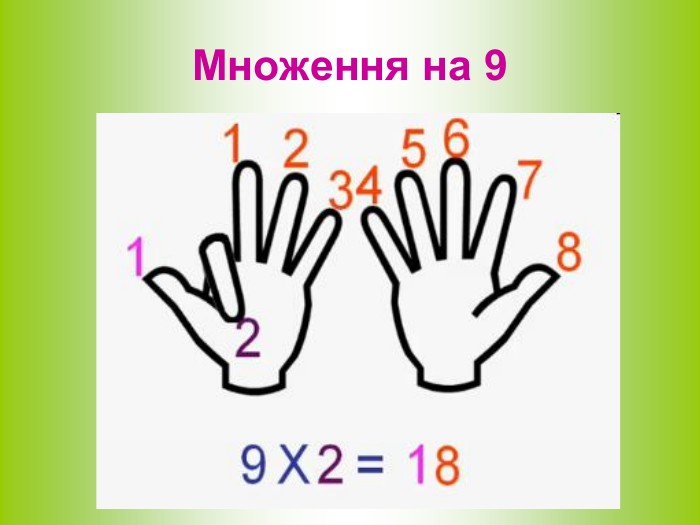
Мета уроку: Узагальнити та систематизувати знання про зміст дії множення натуральних чисел; про переставну та сполучну властивості множення; повторити властивості множення на 0 та 1; повторити та закріпити назви компонентів множення; формувати уміння та навички множити письмово багатоцифрові натуральні числа (множення „в стовпчик”)

За всю історію людства було придумано багато способів множення. Лише в кінці XV - початку XVI століття італійський математик Лука Пачолі приводить 8 різних способів множення в своєму трактаті про арифметику.

Знак множення «навскісний хрест» ( ) вперше в 1631 році ввів англійський математик Уїльям Оутред (1575 – 1660) Пізніше, в 1698 році, видатний німецький математик Г. Лейбніц (1646 – 1716) запропонував дію множення позначати крапкою (·)

Володимир Іванович Даль - автор «Тлумачного словника живої мови» в своєму словнику пише: Умножати, множити, збільшувати числом, кількістю.

Чи означає це, що між множенням і додаванням є щось спільне? Множення можна представити за допомогою додавання. Наприклад, я живу в трикімнатній квартирі. У кожній кімнаті у мене лежить по два яблука. Скільки всього яблук?

Помножити число а на число b – означає знайти суму b доданків, кожен з яких дорівнює а.

Множення - це додавання однакових доданків. Помножити число 2 на 3 означає знайти суму трьох доданків, кожний з яких дорівнює 2. 2 Х 3 = 6 перший другий добуток множник множник Числа, які множать, називають МНОЖНИКАМИ. Число, яке дістають при множенні, називають ДОБУТКОМ.

Записати суму через добуток:

Записати добуток через суму: 122 + 122 + 122 19 + 19+ 19 + 19 + 19 с + с + с + с + с + с + с (х – у) + (х – у)

Перевіримо таблицю множення

Перевірте правильність виконання дій. Виправте помилки: + + + + +

Полічити число кроликів, зображених на малюнку 4+4+4+4+4+4+4+4+4=36 9+9+9+9=36 4· 9=36 9· 4=36 Отже, 4· 9 = 9· 4

Сформулюйте властивість Від перестановки множників добуток не зміниться.

0 На нуль скільки не множ, все нуль і буде. В. І. Даль

При множенні будь якого числа на нуль завжди буде нуль.

6 11 78 123 Сформулюйте властивість

При множенні будь – якого числа на одиницю завжди отримаємо те ж саме число.

Знайдіть добуток: 15000

Сформулюйте властивість Від порядку групування множників добуток не змінюється.

Обчисліть зручним способом: 245300

23500 42420 164200 2700

Спростити вирази: 7600у 100ху 3500х 300аb

Перевірте, чи всі нерівності правильні. Виправте помилки :

Розв'яжіть задачу, складаючи вираз Бочка вміщає води в 9 разів більше, ніж чотири відра. Скільки літрів води вміщає бочка, якщо в одне відро входить 8л води? Розв'язання

288

Множення в “стовпчик”

Щоб помножити натуральне число на 10, 100, 1000, …, треба приписати до цього числа праворуч стільки нулів, скільки їх у числі, на яке множимо. Щоб помножити натуральні числа, які закінчуються нулями, треба: 1) виконати множення, не звертаючи уваги на нулі в кінці чисел; 2)до знайденого добутку приписати праворуч стільки нулів, скільки їх у всіх множниках разом.

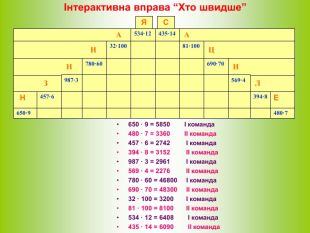
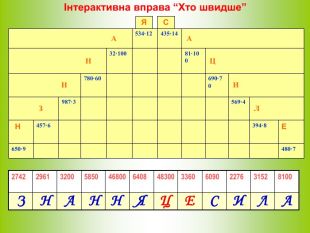
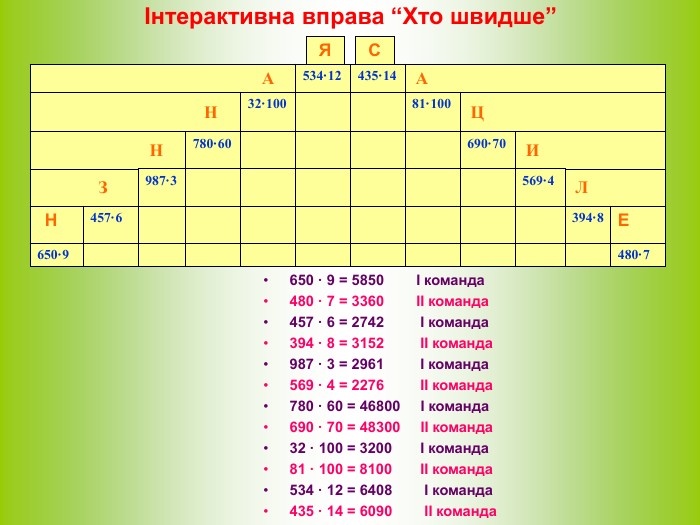
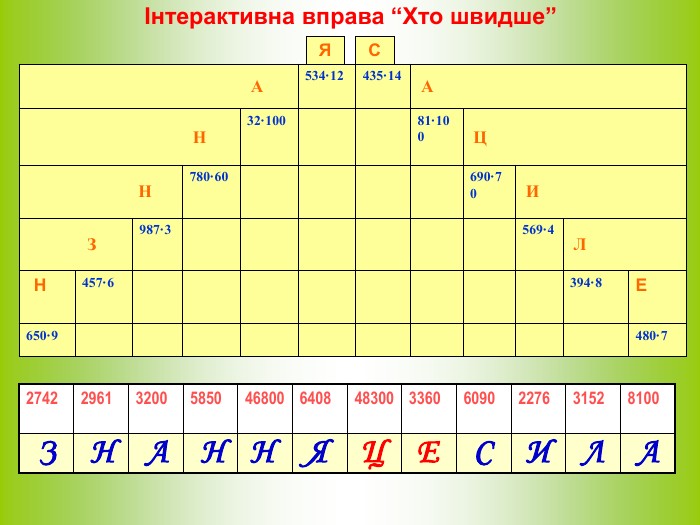
 А  А Н  Ц   Н  И   З  Л Н Е Інтерактивна вправа “Хто швидше” С Я 650 · 9 = 5850 І команда 480 · 7 = 3360 ІІ команда 457 · 6 = 2742 І команда 394 · 8 = 3152 ІІ команда 987 · 3 = 2961 І команда 569 · 4 = 2276 ІІ команда 780 · 60 = 46800 І команда 690 · 70 = 48300 ІІ команда 32 · 100 = 3200 І команда 81 · 100 = 8100 ІІ команда 534 · 12 = 6408 І команда 435 · 14 = 6090 ІІ команда

 А  А Н  Ц   Н  И   З  Л Н Е Інтерактивна вправа “Хто швидше” С Я 2742 2961 3200 5850 46800 6408 48300 3360 6090 2276 3152 8100 З Н А Н Н Я Ц Е С И Л А

Історична довідка У Стародавньому Римі та Стародавній Греції дії множення вважалися дуже важкими. Той, хто вмів їх виконувати, цінувався на вагу золота. Таких людей купці завжди наймали для виконання різних обчислень. За тисячі років розвитку математики було придумано велику кількість способів множення чисел. Італійський математик Лука Пачолі у своєму трактаті “Сума знань з арифметики, відношенням та пропорційності “ наводить 8 різноманітних методів множення. У Росії найчастіше користувалися так званим “російським способом множення”, який полягав у послідовному множенні та діленні на 2. Приклад 26 •32 26 32 52 16 104 8 208 4 416 2 832 1 Отже, 26•32 = 52•16 = 104•8 = 208•4 = 416•2 = 832•1=832.

Множення на 9

Як множили китайці

3 5 8 24 40

Підсумок уроку Що вивчили сьогодні на уроці? Як у запису а · b = с називається число а? число b? число с? Які числа треба поставити замість □, щоб рівність була правильною? 1) 5 + 5 + 5 = 5 · □ ; 2) 6 · □ = 6; 3) 6 · □ = 0; 4) 6 · □ = 3 · □ Обчислити усно: 123• 8 •0 •1254 •76

Математику тому вивчати слід, що вона розум до ладу приводить. М. Ломоносов Математика – це наука, яка вимагає найбільше фантазії. С. Ковалевська Пам'ятай