Навчальна програма 7 клас. Алгебра. НУШ.

Про матеріал

НАВЧАЛЬНА ПРОГРАМА ДЛЯ 7 КЛАСУ Розроблена на основі модельної програми «Алгебра. 7-9 класи» для закладів загальної середньої освіти (автор Істер О.С.) «Рекомендовано Міністерством освіти і науки України» (наказ Міністерства освіти і науки України від 24.07.2023 № 883

Перегляд файлу

(назва закладу освіти)

ЗАТВЕРДЖЕНО

Рішення педагогічної ради

від «___»________________202_ р.,

АЛГЕБРА

НАВЧАЛЬНА ПРОГРАМА ДЛЯ 7 КЛАСУ

Розроблена на основі модельної програми

«Алгебра. 7-9 класи»

для закладів загальної середньої освіти

(автор Істер О.С.)

«Рекомендовано Міністерством освіти і науки України» (наказ Міністерства освіти і науки України від 24.07.2023 № 883

Укладач: ____________________

2024
Вступ

Навчальна програма з алгебри для 7 класу закладу загальної середньої освіти побудована відповідно до Закону України «Про повну загальну середню освіту» від 16 січня 2020 року № 463-IX, Державного стандарту базової середньої освіти, затвердженого постановою Кабінету Міністрів України від 30 вересня 2020 року № 898, Типової освітньої програми для 5–9 класів закладів загальної середньої освіти, затвердженої наказом Міністерства освіти і науки України від 19 лютого 2021 року № 235, модельної навчальної програми «Алгебра. 7-9 класи» для закладів загальної середньої освіти (автор Істер О), рекомендованої Міністерством освіти і науки України (наказ Міністерства освіти і науки України від 24.07.2023 № 883) та спрямована на реалізацію вимог до обов’язкових результатів навчання, визначених Державним стандартом для математичної освітньої галузі.

Мета і завдання навчальної програми

Метою базової середньої освіти є розвиток природних здібностей, інтересів, обдарувань учнів, формування компетентностей, необхідних для їхньої соціалізації та громадянської активності, свідомого вибору подальшого життєвого шляху та самореалізації, продовження навчання на рівні профільної освіти або здобуття професії, виховання відповідального, шанобливого ставлення до родини, суспільства, навколишнього природного середовища, національних та культурних цінностей українського народу. Реалізація мети базової середньої освіти ґрунтується на таких ціннісних орієнтирах, як:

повага до особистості учня та визнання пріоритету його інтересів, досвіду, власного вибору, прагнень, ставлення у визначенні мети та організації освітнього процесу, підтримка пізнавального інтересу та наполегливості;
створення освітнього середовища, у якому забезпечено атмосферу довіри та рівного доступу кожного учня до освіти без будь-яких форм дискримінації учасників освітнього процесу та проявів насильства (булінгу);
дотримання принципів академічної доброчесності у взаємодії учасників освітнього процесу та організації всіх видів навчальної діяльності;
становлення вільної особистості учня, підтримка його самостійності, підприємливості та ініціативності, розвиток критичного мислення та впевненості в собі;
формування культури здорового способу життя учня, створення умов для забезпечення його гармонійного фізичного та психічного розвитку, добробуту;
утвердження людської гідності, чесності, милосердя, доброти, справедливості, співпереживання, взаємоповаги і взаємодопомоги, поваги до прав і свобод людини, здатності до конструктивної взаємодії учнів між собою та з дорослими;
формування в учнів активної громадянської позиції, патріотизму, поваги до культурних цінностей українського народу, його історико-культурного надбання і традицій, державної мови;
плекання в учнів любові до рідного краю, відповідального ставлення до довкілля.

Метою математичної освітньої галузі є розвиток особистості учня через формування математичної компетентності у взаємозв’язку з іншими ключовими компетентностями для успішної освітньої та подальшої професійної діяльності впродовж життя, що передбачає:

засвоєння системи знань, удосконалення вміння розв’язувати математичні та практичні задачі;
розвиток логічного мислення та психічних властивостей особистості;

розуміння можливостей застосування математики в особистому та суспільному житті.

Вважаючи на сучасний стан розвитку суспільства та потреби сьогодення, одним із основних викликів є збереження та подальше підвищення статусу України як провідної світової держави в наукомістких галузях, зокрема в комп’ютерних та інформаційних дисциплінах, авіаційній та космічній галузях; проведення наукових досліджень і технічних розробок на сучасному світовому рівні; розвиток технологічного, економічного й оборонного потенціалу держави; інтенсивний розвиток усіх галузей народного господарства та оновлення виробничої бази на засадах сучасних технологій, автоматизації та роботизації; масова інформатизація та комп’ютеризація. Зазначені виклики можуть бути реалізовані виключно за умови масового набуття підростаючим поколінням компетенцій, що є чільними для професійної орієнтації в науко- містких областях, конструктивного логічного та алгоритмічного мислення, високого рівня технічної грамотності. І провідним інструментом для цього є навчання математики як мови науки, техніки та технологій.

Наскрізні лінії та їх реалізація

Курс алгебри в 7 класі закладів загальної середньої освіти логічно продовжує реалізацію завдань математичної освіти здобувачів освіти, розпочату в початковій школі та 5–6 класах середньої школи, розширюючи та доповнюючи ці завдання відповідно до вікових і пізнавальних можливостей здобувачів освіти.

Програма передбачає формування й розвиток в учнів ключових компетентностей зазначених Державним стандартом базової середньої освіти, та спільних для них наскрізних умінь. Цей процес відбувається в ході опанування змісту та досягнення очікуваних конкретних результатів навчання, які визначає модельна навчальна програма.

У курсі алгебри 7 – 9 класів можна назвати такі основні змістові лінії: арифметика; алгебра; функції; дані, статистика та ймовірність.

Курс алгебри 7 класу містить три змістові лінії : арифметика, алгебра, функції.

Змістова лінія «Арифметика» є базою для подальшого вивчення учнями математики, сприяє розвитку їхнього логічного мислення, формуванню вміння користуватися алгоритмами, а також набуттю практичних навичок, потрібних у повсякденному житті. Розвиток поняття про число в основній школі пов’язаний з раціональними числами.

Змістова лінія «Алгебра» сприяє формуванню в учнів математичного апарату для розв’язування завдань із розділів математики, суміжних предметів і реальності. Мова алгебри підкреслює значення математики як мови для побудови математичних моделей процесів та явищ навколишнього світу. Розвиток алгоритмічного мислення, потрібного, зокрема, для освоєння курсу інформатики та оволодіння навичками дедуктивних міркувань, також є завданнями вивчення алгебри.

Змістова лінія «Функції» спрямована на отримання школярами конкретних знань про функції як найважливіші математичні моделі для опису та дослідження різноманітних процесів. Вивчення цього матеріалу сприяє розвитку в учнів уміння використовувати різні мови математики (словесну, символічну, графічну, табличну), робить внесок у формування уявлень про роль математики в розвитку цивілізації та культури.

Основними завданнями курсу алгебри 7 класу є формування вмінь виконувати тотожні перетворення цілих і дробових виразів, розв’язувати рівняння та їх системи, використовувати функціональні залежності між змінними величинами, достатніми для вільного їх використання у вивченні математики і суміжних предметів, а також для практичних застосувань. Важливе завдання полягає в залученні здобувачів освіти до використання рівнянь та їх систем, а також функцій як засобів математичного моделювання реальних процесів і явищ, розв’язування на цій основі прикладних та інших задач. У процесі вивчення курсу посилюється роль обґрунтувань математичних тверджень, індуктивних і дедуктивних міркувань, формування різноманітних алгоритмів, що має сприяти розвитку логічного мислення та алгоритмічної культури здобувачів освіти.

Основу курсу становлять перетворення раціональних виразів, вводяться нові поняття «одночлен», «многочлен» та формули скороченого множення, тотожності, тотожні перетворення виразів. Важливо забезпечити формування вмінь здобувачів освіти виконувати основні види перетворень таких виразів, що є передумовою подальшого успішного засвоєння курсу та використання математичного апарату під час вивчення інших шкільних предметів. Розглядається поняття степеня з натуральним показником та його властивості.

Істотного розвитку набуває змістова лінія рівнянь. Процес розв’язування рівняння трактується як послідовна заміна даного рівняння рівносильними йому рівняннями. На основі узагальнення відомостей про рівняння, здобутих у попередні роки, вводиться поняття лінійного рівняння з однією змінною. Курс передбачає вивчення лінійних рівнянь, та рівнянь, які зводяться до лінійних.

Значне місце відводиться застосуванню рівнянь, до розв’язування різноманітних задач, у тому числі прикладного змісту. Ця робота пронизує всі теми курсу. Важливе значення надано формуванню вміння створювати математичну модель задачі у вигляді рівняння або системи рівнянь і надалі –застосовуванню відповідного алгоритму для розв’язування створеної математичної моделі та трактуванню отриманої відповіді.

У 7 класі вводиться одне з фундаментальних математичних понять – поняття функції. У цьому ж класі розглядається лінійна функція та її графік. Функціональна лінія пронизує весь курс алгебри наступних класів.. Властивості функцій зазвичай встановлюються за їх графіками, на основі наочних уявлень, і лише деякі властивості обґрунтовуються аналітично. У міру оволодіння здобувачами освіти теоретичним матеріалом кількість властивостей, що підлягають вивченню, поступово збільшується. Під час вивчення функцій чільне місце відводиться формуванню вмінь будувати й аналізувати графіки функцій, характеризувати за графіками функцій процеси, які вони описують, спроможності розуміти функцію як певну математичну модель реального процесу.

Крім реалізації зазначених наскрізних ліній, у ході вивчення курсу математики формуються наскрізні вміння ключових компетентностей, визначені в Державному стандарті.

Структура програми

Програму представлено в табличній формі, що містить чотири частини: очікувані результати навчально-пізнавальної діяльності учнів та зміст навчального матеріалу, необхідний для їх досягнення; ключові компетентності та види навчальної діяльності. У правій частині вказано навчальний матеріал, який підлягає вивченню у відповідному класі. У лівій частині ключові компетентності та види навчальної діяльності, які будуть застосовуватися при формуванні знань та умінь. Очікувані результати навчально-пізнавальної діяльності учнів орієнтують на результати навчання, які є об’єктом контролю й оцінювання.

ПРОГРАМА

Назва теми	Кількість годин
Повторення навчального матеріалу за 5-6 класи	7
Цілі вирази	46
Функції	14
Лінійні рівняння з однією змінною. Системи лінійних рівнянь з двома змінними.	23
Повторення матеріалу за навчальний рік	12
Резерв часу.	4
Всього	105

Складено відповідно підручника «Алгебра»

для 7 класу закладів загальної середньої освіти автора: О.С. Істер — Київ: Генеза, 2024 та модельною навчальною програмою «Алгебра. 7-9 класи» для закладів загальної середньої освіти (автор Істер О. С.)

Очікувані результати навчально-пізнавальної діяльності учнів

Зміст навчального матеріалу

Ключові компетентності

Види навчальної діяльності

Тема 1. Цілі вирази (46 год)

Розуміє, що таке числовий вираз, вираз зі змінними;

розрізняє: числові вирази та вирази зі змінними; одночлени серед інших алгебраїчних виразів,одночлени стандартного вигляду серед інших одночленів, подібні одночлени; многочлени серед інших алгебраїчних виразів, многочлени стандартного вигляду серед інших многочленів, подібні члени многочлена; многочлени, для перетворення яких можна застосовувати формули, які вказано в змісті;

читає числові вирази та вирази зі змінними, використовуючи математичну термінологію;

записує числові вирази та вирази зі змінними, подані в текстовій формі, з використанням математичної символіки; наводить приклади: числових виразів; виразів зі змінними; одночленів та одночленів стандартного вигляду; многочленів та многочленів стандартного вигляду; пояснює: · як знайти числове значення виразу зі змінними при заданих значеннях змінних; · що таке тотожні вирази, тотожність, тотожне перетворення виразу, одночлен стандартного вигляду, коефіцієнт; многочлен стандартного вигляду;

розуміє: · сутність дії піднесення до степеня з натуральним показником;і розкладання многочлена на множники; · правила додавання, віднімання і множення многочленів; · доведення властивостей степеня з натуральним показником; формулює: · означення одночлена, степеня з натуральним показником; многочлена, подібних членів многочлена, степеня многочлена; · властивості степеня з натуральним показником; · правила множення одночлена і многочлена, множення двох многочленів;

записує та обґрунтовує: · властивості степеня з натуральним показником; · формули скороченого множення; розв’язує вправи, що передбачають: обчислення значення числового виразу та виразу зі змінними із заданим значенням змінних; тотожні перетворення виразів та доведення тотожностей; застосування властивостей степеня з натуральним показником для спрощення виразів та обчислення їхніх значень; зведення одночлена до стандартного вигляду; визначення коефіцієнта і степеня одночлена; множення одночленів та піднесення одночлена до степеня; зведення подібних членів многочлена; визначення степеня многочлена; перетворення добутку одночлена і многочлена, суми, різниці, добутку двох многочленів у многочлен; розкладання многочлена на множники способом винесення спільного множника за дужки, способом групування, за формулами скороченого множення та із застосуванням кількох способів; використання зазначених перетворень для спрощення виразів, доведення тотожностей, обчислення значень виразів, розв’язування рівнянь, задач на подільність цілих чисел тощо.

Вирази зі змінними.

Цілі раціональні вирази.

Тотожність.

Тотожні перетворення виразу.

Степінь з натуральним показником.

Властивості степеня з натуральним показником.

Одночлен.

Піднесення одночленів до степеня.

Множення одночленів.

Многочлен.

Подібні члени многочлена та їх зведення.

Степінь многочлена.

Додавання, віднімання і множення многочленів.

Формули квадрата двочлена, різниці квадратів, суми і різниці кубів.

Розкладання многочленів на множники

Чітко і зрозуміло формулює думки, аргументує, ставить запитання і розпізнає проблеми, формулює висновки на основі інформації, поданої в різних формах, доречно та коректно вживає в мовленні математичну термінологію. Оперує текстовою і числовою інформацією, встановлює кількісні та просторові відношення між реальними об’єктами навколишньої дійсності (природними, культурними, технічними тощо),

Обирає, створює і досліджує найпростіші математичні моделі реальних об’єктів, процесів і явищ, інтерпретує та оцінює результати, шукає пояснення та оцінювати правильність аргументів, усвідомлення важливості математики як мови науки, техніки та технологій.

Будує та досліджує математичні моделі природних явищ і процесів, робить висновки на основі міркувань та свідчень, генерує нові ідеї щодо розв’язання проблемної ситуації, аналізує та планує їхнє втілення.

Структурує дані, діє за алгоритмом та складає алгоритм, оцінює достовірність інформації, доводить істинність тверджень; критичне осмислення інформації та джерел її отримання, усвідомлює важливості інформаційно-комунікаційних технологій для ефективного розв’язання математичних задач.

Усвідомлює власні освітні потреби та цінності нових знань і умінь, зацікавлений у пізнанні світу та розуміє важливості навчання впродовж життя, прагнення вдосконалювати результати людської діяльності.

Висловлює власну думку, слухає і чує інших осіб, оцінює аргументи та змінює думку на основі доказів, аналізує і критично оцінює події у державі на основі статистичних даних, враховувати правові, етичні й соціальні наслідки прийняття рішень, розпізнає інформаційні маніпуляції, налаштованість на логічне обґрунтування позиції без передчасного переходу до висновків.

Співпрацює в команді для розв’язання проблеми, аргументує та обстоює власну позицію, приймає аргументовані рішення на основі аналізу всіх даних та формує причинно-наслідкових зв’язків проблемної ситуації. Бачить застосування вивченого матеріалу у повсякденному житті, створює моделі, здійснює необхідні розрахунки.

Фронтальна форма на вчання, яка включає слухання пояснень вчителя/вчительки, слухання та аналіз учнями/ученицями ви словлювань інших учнів/учениць.

Фронтальна робота. Виконання вправ (усно та письмово), передбачених очікуваними результатами навчання. Колективне розв’язання проблем- них ситуацій.

Самостійна робота. Виконання самостійних і тематичних контрольних робіт, інших видів робіт; виконання домашньої роботи.

Групова робота. Робота в парах.

Індивідуальна робота, яка включає: самостійну роботу з підручником;

самостійне виконан ня завдань біля дошки або в зошиті під час уроку;

пошук інформації в Інтернеті.

Роботу з додатковою

літературою.

Дидактичні ігри

Проектна діяльність.

Функції (16 годин)

Наводить приклади: функціональних залежностей; лінійних функцій; розуміє: · які залежності між величинами є функціональними; · сутність поняття функції; · що пряма пропорційність є окремим видом лінійної функції; пояснює, що таке: аргумент; функція; область визначення функції; область значень функції; графік функції; формулює означення понять: функція; графік функції; лінійна функція; пряма пропорційність; розпізнає лінійну функцію та пряму пропорційність серед інших функцій; усвідомлює, що лінійні функції можуть слугувати математичними моделями реальних життєвих ситуацій; називає та ілюструє на прикладах способи задання функції; описує побудову графіка функції, зокрема, лінійної та її окремого виду – прямої пропорційності; розв’язує вправи, що передбачають: знаходження області визначення функції; знаходження значення функції за даним значенням аргументу; побудову графіка лінійної функції; знаходження за графіком функції значення функції за даним значенням аргументу і навпаки; визначення окремих характеристик функції за її графіком (нулі, додатні значення, від’ємні значення); використовує лінійну функцію та її графік для моделювання реальних процесів.

Функціональна залежність між величинами як математична модель реальних процесів.

Функція.

Область визначення та область значень функції.

Способи задання функції.

Графік функції.

Лінійна функція, її графік та властивості

Обирає, створює і досліджує найпростіші математичні моделі

реальних об’єктів, процесів і явищ, інтерпретує та оцінює результати, шукає пояснення та оцінювати правильність аргументів, усвідомлення важливості математики як мови науки, техніки та технологій.

Будує та досліджує графіки лінійних функцій, математичні моделі природних явищ і процесів, робить висновки на основі міркувань та свідчень, генерує нові ідеї щодо розв’язання проблемної ситуації, аналізує та планує їхнє втілення.

Групова робота. Робота в парах.

Індивідуальна робота, яка включає: самостійну роботу з підручником;

самостійне виконан ня завдань біля дошки або в зошиті під час уроку;

пошук інформації в Інтернеті.

Роботу з додатковою

літературою.

Дидактичні ігри

Проектна діяльність.

Лінійні рівняння з однією змінною. Системи лінійних рівнянь з двома змінними. (23 год)

Розпізнає лінійне рівняння з однією змінною серед даних рівнянь;

наводить приклади: рівносильних рівнянь; лінійних рівнянь з однією змінною; лінійних рівнянь з однією змінною, які мають один корінь, безліч коренів, не мають коренів;

формулює: · означення рівняння, кореня (розв’язку) рівняння, рівносильних рівнянь, лінійного рівняння з однією змінною; · основні властивості рівняння; пояснює: · що означає розв’язати рівняння; · що таке рівносильні рівняння; · за допомогою яких перетворень даного рівняння можна отримати рівняння, рівносильне даному; характеризує: · випадки, коли лінійне рівняння з однією змінною має один розв’язок; має безліч розв’язків; не має

розв’язків; · етапи розв’язування задачі за допомогою рівняння; усвідомлює, що лінійні рівняння з однією змінною та рівняння, які зводяться до лінійних, можуть слугувати математичними моделями реальних життєвих ситуацій; складає рівняння за умовою текстової задачі;

розв’язує: лінійні рівняння з однією змінною і рівняння, що зводяться до них; текстові задачі за допомогою лінійних рівнянь з однією змінною;

створює математичну модель задачі у вигляді рівняння; розв’язує сюжетні задачі з реальними даними щодо: безпеки руху; розрахунку сімейного бюджету, можливості здійснення масштабних покупок; безпеки і охорони здоров’я; практичних аспектів фінансових питань.

Розпізнає рівняння з двома змінними, лінійні рівняння з двома змінними серед інших рівнянь;

наводить приклади: рівняння з двома змінними; лінійного рівняння з двома змінними; системи двох лінійних рівнянь з двома змінними;

формулює означення: лінійного рівняння з двома змінними; розв’язку рівняння з двома змінними; розв’язку системи двох лінійних рівнянь з двома змінними; пояснює: · що означає розв’язати рівняння з двома змінними, систему рівнянь з двома змінними; · що таке графік рівняння з двома змінними; будує графіки лінійних рівнянь з двома змінними;

розв'язує сюжетні задачі: на рух з точки зору його безпеки; на розпорядження власними та родинними фінансами; фінансового змісту крізь призму історичних подій тощо.

Загальні відомості про рівняння.

Рівносильні рівняння.

Лінійні рівняння з однією змінною.

Розв’язування лінійних рівнянь.

Розв’язування задач за допомогою лінійних рівнянь.

Рівняння як математична модель задач

Рівняння з двома змінними.

Розв’язок рівняння з двома змінними.

Графік рівняння з двома змінними.

Лінійне рівняння з двома змінними та його графік.

Система двох лінійних рівнянь з двома змінними та її розв’язок.

Розв’язування систем двох лінійних рівнянь з двома змінними: графічним способом; способом підстановки; способом додавання.

Розв’язування задач за допомогою систем лiнійних рівнянь.

Система двох лінійних рівнянь з двома змінними як математична модель задач

Обирає, створює і досліджує найпростіші математичні моделі

Групова робота. Робота в парах.

Індивідуальна робота, яка включає: самостійну роботу з підручником;

самостійне виконан ня завдань біля дошки або в зошиті під час уроку;

пошук інформації в Інтернеті.

Роботу з додатковою

літературою.

Дидактичні ігри

Проектна діяльність.

Додаткові теми

Ділення одночлена на одночлен.

Квадрат суми трьох виразів.

Куб суми та куб різниці двох виразів.

Формули для розкладання на множники виразів виду aⁿ – bⁿ і aⁿ + bⁿ.

Взаємне розташування графіків двох лінійних функцій.

Розв’язування лінійних рівнянь з параметрами.

Лінійне рівняння з трьома змінними.

Система лінійних рівнянь з трьома змінними

Система оцінювання результатів навчання

До навчальних досягнень учнів з математики, які підлягають оцінюванню, належать:

– теоретичні знання, що стосуються математичних понять, тверджень, теорем, властивостей, ознак, методів та ідей математики;

– знання, що стосуються способів діяльності, які можна подати у вигляді системи дій (правила, алгоритми);

– здатність безпосередньо здійснювати уже відомі способи діяльності відповідно до засвоєних правил, алгоритмів (наприклад, виконувати певне тотожне перетворення виразу, розв’язувати рівняння певного виду, виконувати геометричні побудови, досліджувати функцію на монотонність, розв’язувати текстові задачі розглянутих типів тощо);

– здатність застосовувати набуті знання і вміння для розв’язання навчальних і практичних задач, коли шлях, спосіб такого розв’язання потрібно попередньо визначити (знайти) самому.

Основними видами оцінювання результатів навчання учнів, що проводяться закладом, є формувальне, поточне та підсумкове (тематичне, семестрове, річне).

Система оцінювання (бальна/рівнева):

• 10, 11, 12 – високий рівень

• 7, 8, 9 – достатній рівень

• 4, 5, 6 – середній рівень

• 1, 2, 3 – початковий рівень

Оцінювання якості математичної підготовки учнів з математики здійснюється в двох аспектах: рівень оволодіння теоретичними знаннямита якість практичних умінь і навичок, здатність застосовувати вивчений матеріал під час розв’язування задач і вправ.

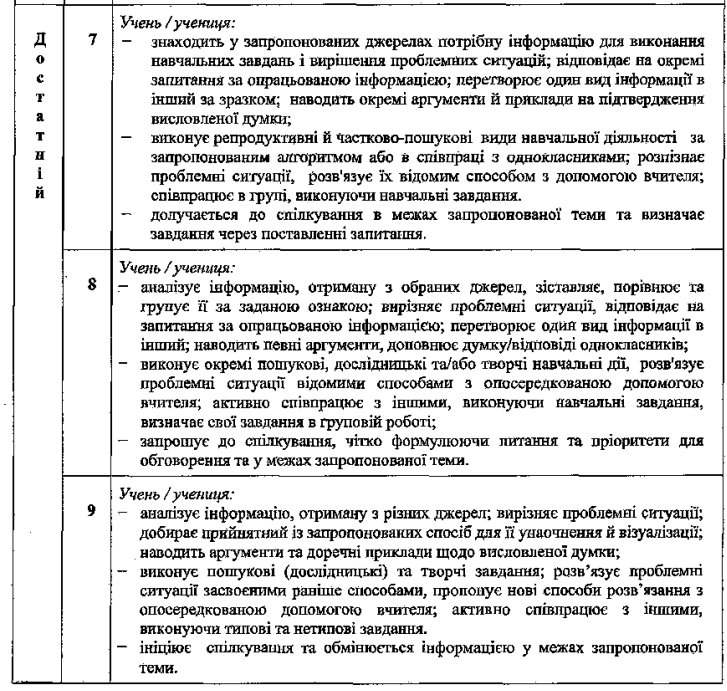
КРИТЕРІЇ оцінювання навчальних досягнень учнів

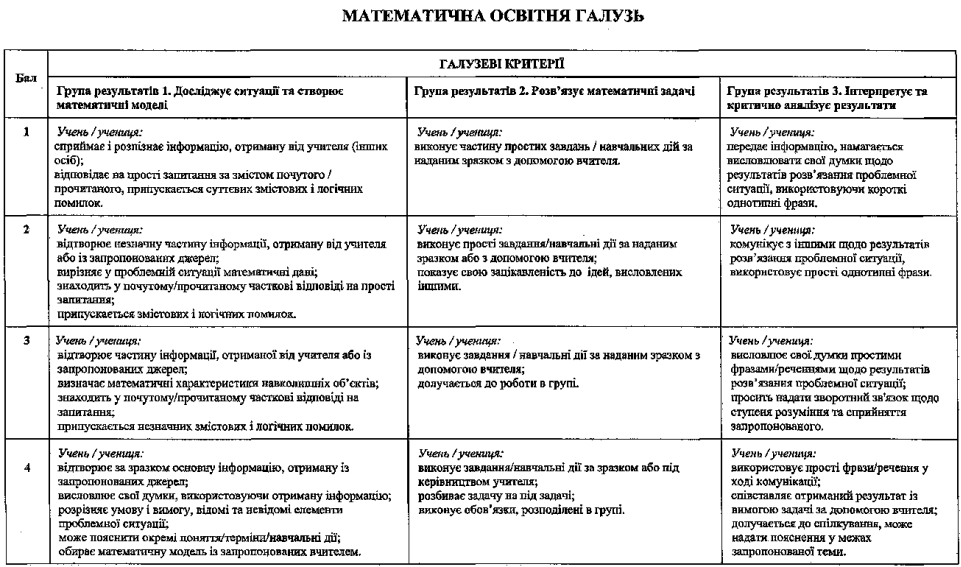
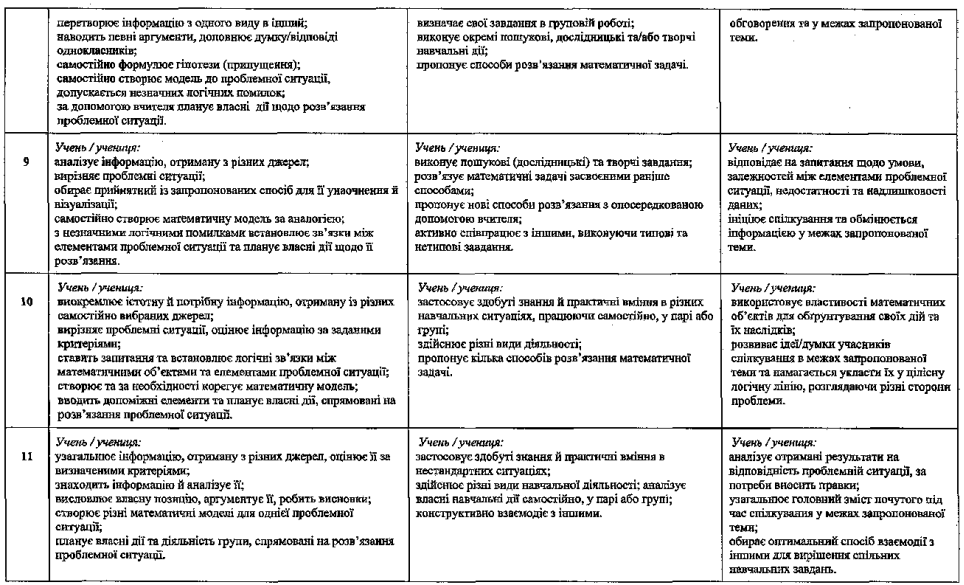
Оцінкою роботи є сума балів, отримана учнем за виконання кожного завдання окремо. Якщо сумою є неціле число балів, то користуємося правилом округлення.

Виправлення і закреслення в оформленні розв’язання завдань, якщо вони зроблені акуратно не є підставою для зниження оцінки.

Тематичне оцінювання здійснюється на основі поточного оцінювання із урахуванням проміжних (самостійні роботи) і тематичних (контрольні роботи).

Оцінка за семестр ставиться за результатами тематичних. При цьому мають враховуватися динаміка особистих навчальних досягнень учнів з предмета протягом семестру, важливість теми, тривалість її вивчення, складність змісту тощо.

Річне оцінювання здійснюється на підставі загальної оцінки результатів навчання за І та ІІ семестри або скоригованих семестрових оцінок. Річна оцінка не обов’язково є середнім арифметичним від оцінок за І та ІІ семестри. При виставленні річної оцінки мають враховуватися:

важливість тем, які вивчались у І та ІІ семестрах;
тривалість їх вивчення та складність змісту;
динаміка особистих навчальних досягнень учня з предмета протягом року;
уміння застосовувати учнем набуті протягом навчального року знання тощ

Середня оцінка розробки

Структурованість

5.0

Оригінальність викладу

5.0

Відповідність темі

5.0

Загальна:

5.0

Всього відгуків: 6

Оцінки та відгуки

Лисенко Галина 08.09.2024 в 18:07

Загальна:

5.0

Структурованість

5.0

Оригінальність викладу

5.0

Відповідність темі

5.0
Юнікова Валентина 01.09.2024 в 13:41

Загальна:

5.0

Структурованість

5.0

Оригінальність викладу

5.0

Відповідність темі

5.0
Бабій Любов 01.09.2024 в 12:33

Загальна:

5.0

Структурованість

5.0

Оригінальність викладу

5.0

Відповідність темі

5.0
Циганок Лариса Анатоліївна 31.08.2024 в 17:31

Неймовірна робота. Дякую.)))

Загальна:

5.0

Структурованість

5.0

Оригінальність викладу

5.0

Відповідність темі

5.0
Мисік Марина Олександрівна 30.08.2024 в 10:33

Загальна:

5.0

Структурованість

5.0

Оригінальність викладу

5.0

Відповідність темі

5.0
Сенека Виктор 22.08.2024 в 15:42

Загальна:

5.0

Структурованість

5.0

Оригінальність викладу

5.0

Відповідність темі

5.0

Показати ще 3 відгука

docx

Завантажити

Зберегти на потім

Додав(-ла)

Тягілєва Надія Василівна

Пов’язані теми

Алгебра, 7 клас, Інші матеріали

До підручника

Алгебра 7 клас (Істер О.С.)

Додано

10 серпня

Переглядів

9962

Оцінка розробки

5.0 (6 відгуків)