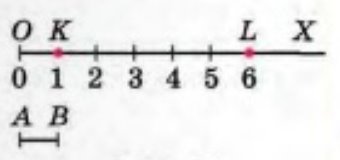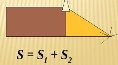Навчальний посібник "Математика 5 клас" 1 семестр

Про матеріал

Посібник та уроки в ньому розроблений згідно Комбінованої системи М.П. Гузика і може бути використаний як додатковий матеріал для учнів на уроки. Він складається з шести тем. Кожна тема має таку структуру:

перший урок – урок розбору блоку навчальної інформації;
наступні уроки – уроки фронтального опрацювання матеріалу,
між уроками фронтального опрацювання містяться завдання по підготовці до уроків індивідуального опрацювання матеріалу;
в кінці кожної теми є один урок внутрішньопредметного узагальнення матеріалу, на якому кожен продемонструє свої знання блоку, а також узагальнить знання і вміння, здобуті під час теми.

Перегляд файлу

Шановний п’ятикласнику!

Ти продовжуєш вивчати одну з найдавніших і найважливіших наук – математику. У цьому тобі допоможе навчальний посібник, який ти тримаєш в руках.

Посібник складається з шести тем. Кожна тема має таку структуру:

перший урок – урок розбору блоку навчальної інформації;
наступні уроки – уроки фронтального опрацювання матеріалу, на яких ти зможеш засвоїти поняття, терміни і правила блоку навчальної інформації, також навчитись застосовувати ці знання для розв’язування різноманітних задач і вправ.
між уроками фронтального опрацювання ти будеш виконувати завдання індивідуального опрацювання матеріалу, вправи якого не наведені в даному посібнику. Але він містить завдання для підготовки до індивідуального опрацювання, позначені
в кінці кожної теми є один урок внутрішньопредметного узагальнення матеріалу, на якому кожен продемонструє свої знання блоку, а також узагальнить знання і вміння, здобуті під час теми.

Нехай Бог посилає тобі мудрості у вивченні математики!!!

Тема №1. Натуральні числа

Урок №1

Натуральні числа

«Ледача рука до убозтва

веде, рука ж роботяща збагачує»

Книга приповістей Соломонових 10:4

Питання

Натуральні числа. Число нуль. Цифри. Десятковий запис натуральних чисел.
Порівняння натуральних чисел.
Додавання натуральних чисел. Властивості додавання.
Віднімання натуральних чисел

Література

Істер О.С. Математика: підручник для 5 класу загальноосвітніх навчальних закладів. – §§1 – 4, ст. 11 – 40.

1. Натуральні числа. Число нуль. Цифри. Десятковий запис натуральних чисел

1.1

Числа, які використовуються при лічбі предметів, називаються натуральними.

1; 25; 1028

1.2

Натуральні числа використовуються також для визначення порядку розміщення предметів.

Перший, двадцять п’ятий

1.3

Цифри – це спеціальні значки для запису чисел.

0, 1, 2, 3. 4, 5, 6, 7, 8, 9

1.4

Запис числа за допомогою десяти цифр називається десятковим.

1.5

Число 0 не є натуральним числом.

1.6

Розряди натуральних чисел

Клас мільярдів			Клас мільйонів			Клас тисяч			Клас одиниць
сотні	десятки	одиниці	сотні	десятки	одиниці	сотні	десятки	одиниці	сотні	десятки	одиниці

1.7

Усі натуральні числа, записані у порядку зростання утворюють натуральний ряд чисел.

1, 2, 3, 4, …, 1020, …

1.8

Властивості натурального ряду:

найменше число – 1;
кожне наступне число більше за попереднє на 1;
найбільшого числа немає.

2. Порівняння натуральних чисел

2.9

Якщо два натуральних числа мають різну кількість знаків (цифр), то більшим буде те, у якого більше знаків.

2.10

Якщо два натуральних числа мають однакову кількість знаків, то більшим числом є те, яке має більше одиниць у найвищому розряді. Якщо кількість одиниць у цьому розряді однакова, то порівнюють число одиниць у наступному розряді і т.д.

3. Додавання натуральних чисел. Властивості додавання

3.11

Числа, які додаються називаються доданками, а число отримане в результаті додавання цих чисел, – сумою.

25 + 31 = 56

25, 31 – доданки ;

56 – сума

3.12

Переставна властивість додавання:

Від перестановки доданків сума не змінюється.

3.13

Сполучна властивість додавання:

Щоб до суми двох чисел додати третє число, можна до першого числа додати суму другого і третього.

4. Віднімання натуральних чисел

4.14

Дія, за допомогою якої за відомою сумою і одним з доданків знаходять другий доданок, називається відніманням.

4.15

Щоб відняти суму від числа, можна від нього відняти один з доданків, а потім від результату відняти другий доданок.

4.16

Щоб відняти число від суми, можна відняти його від одного з доданків і до результату додати другий доданок.

Урок №2

«І все, що тільки чините,

робіть від душі, як Господу, а не людям»

Послання св. апостола Павла до Колосян 3 : 23

Фронтальне опрацювання матеріалу

Ряд натуральних чисел. Цифри. Десятковий запис натуральних чисел

І. Робота над засвоєнням понять, термінів і правил

Завдання 1.

Повторити тези 1.1 – 1.8 блоку №1.
Вставити пропущені слова:

Числа, які використовуються під час лічби предметів, називаються …
Усі натуральні числа, записані у порядку …, утворюють ряд натуральних чисел.
… - це спеціальні значки для запису чисел.
До класу мільйонів відносяться такі розряди: …

Завдання 2.

Виконати усно:

Додайте: 48 і 7; 52 і 49.

Відніміть: від 32 число 8; 7 від 23.

Помножте: 12 і 4; 5 і 20.

Прочитайте число: 1) 94 276; 2) 127 305; 3) 502 900; 4) 1 006 005.

Визначте, в якому випадку записано натуральний ряд:

Квадратів: , , …
Зірочок: , , , …
Чисел: 0, 1, 2, 3,…
Чисел: 1, 4, 5, 7, …
Чисел: 4, 3, 6, 8,…

ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ

Завдання 3.

Сашко зібрався в гості до Дмитрика й запитав його:

В якому під’їзді ти живеш?
В середньому, - відповів Дмитрик.
А який номер під’їзду?
П’ятий.

Скільки під’їздів має будинок Дмитрика?

Запиши сім раз підряд цифру 5. Прочитай отримане число.
Запиши найбільше шестицифрове число. Яке число наступне за ним у натуральному ряді чисел? Які цифри використовуються для запису цього числа?
Запишіть і прочитайте, яке число утвориться, якщо записати число 48 підряд три рази.
Запиши числа у вигляді суми розрядних доданків: 1) 12 312 4734; 2) 5 010 980.
Запишіть словами число 823402504.

Знайди закономірність і продовж ряд чисел (напиши наступні три числа):

Видатний український письменник та громадський діяч Іван Петрович Котляревський народився 9 вересня 1769 року, а помер – 10 листопада 1838 року. Скільки років, місяців і днів прожив Котляревський?

Урок №3

«Хто з мудрими ходить, той мудрим стає,

а хто товаришує з безумним, той лиха набуде»

Книга приповістей Соломонових 13:20

Фронтальне опрацювання матеріалу

Порівняння натуральних чисел

І. Робота над засвоєнням понять, термінів і правил

Завдання 1

Повторити тези 1.1 – 2.10 блоку № 1.
Усно дати відповідь на питання:

Які числа називаються натуральними?
Коли натуральні числа утворюють натуральний ряд?
Який запис чисел називається десятковим?
Які властивості натурального ряду вам відомі?
Як порівняти натуральні числа з різною кількістю знаків?
Як порівняти натуральні числа з однаковою кількістю знаків?

Завдання 2.

Порівняйте числа:

174 і 147;
2001 і 999;
12 369 і 12 371;
3 617 009 і 3 616 356;
7 293 597 326 і 7 293 598 327;
52 000 475 000 і 52 000 574 009.

ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ

Завдання 3.

Розташуйте у порядку спадання числа: 948, 749, 834, 543, 927.
Запишіть усі натуральні числа, які:

більші за 894 і менші від 901;
більші за 3 294 540 і менші за 3 294 547.
1. Яку цифру можна поставити замість зірочки, щоб утворилась правильна нерівність:

.
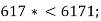
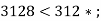
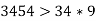
1. Який гарбуз важчий? Визначте це, не додаючи числа (порівняйте).

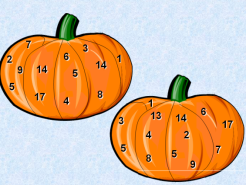
Прочитай подвійні нерівності, де натуральне число

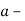
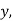
Перелічи всі натуральні числа, замінивши якими букву отримаємо правильну подвійну нерівність:

Готуємось до індивідуального опрацювання матеріалу

Напишіть цифрами число:

сорок вісім мільярдів двісті шістдесят чотири мільйони п’ятсот тридцять дві тисячі сімсот вісімдесят дев’ять;
два мільйони двісті тисяч;
один мільярд сім тисяч шість;

запиши число у вигляді суми розрядних доданків:

Між якими двома найближчими натуральними числами знаходиться число: 1) 16; 2) 374? Відповідь запишіть у вигляді подвійної нерівності.
Знайди різницю найменшого і найбільшого чотирицифрових чисел, які можна записати, використовуючи по одному разу цифри 2, 5, 8 і 0.
Порівняй значення виразів:

Знайди закономірність і продовж ряд чисел (напиши наступні три числа):

Урок №5

«Без бажання все важке, навіть найлегше»

Григорій Сковорода

Фронтальне опрацювання матеріалу

Додавання натуральних чисел. Властивості додавання

І. Робота над засвоєнням понять, термінів і правил

Завдання 1.

Повторити тези 1.1 – 3.13 блоку № 1.
Усно дати відповідь на питання:

Які числа називаються натуральними?
Що таке цифри?
Що називають десятковим записом числа?
Назвати класи у запису натуральних чисел?
Які розряди має кожен клас у запису натуральних чисел?
Що називають натуральним рядом чисел?
Як називаються числа при додаванні?
Сформулювати переставну властивість додавання.
Сформулювати сполучну властивість додавання.

Завдання 2.

Усно виконати вправи:

Прочитайте числа: 34 891; 13 240; 10 101; 937 896; 1 342 789; 5 834 541; 1 001 102.
Вкажіть число вісімнадцять мільйонів три тисячі сто сімдесят п’ять:

А) 183 001 75

Б) 8 003 175

В) 1 831 750 0

Виберіть й вкажіть правильний варіант відповіді: 10км 15м = ?

А) 1015 м

Б) 10 015м

В) 10 150м

ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ

Письмово виконати вправи (стор. 24 – 29):

Завдання 3.

109 (1; 3), 114, 117.

Завдання 4.

119 (2; 4), 129, 131.

ІІІ. Відпрацювання умінь розв’язування нестандартних вправ та задач

Завдання 5.

138, 146.

Урок №6

«Не буде ледачий пекти свого полову,

а людина трудяща набуде маєток цінний»

Книга приповістей Соломонових 12 : 27

Фронтальне опрацювання матеріалу

Віднімання натуральних чисел. Властивості віднімання

І. Робота над засвоєнням понять, термінів і правил

Завдання 1.

Повторити тези 4.14 – 4.16 блоку № 1.
Усно відповісти на питання:

Яка дія називається відніманням?
Як відняти суму від числа?
Як відняти число від суми?

Завдання 2.

2.1. Усно заповнити пропуски у квадраті:

&Kcy;&vcy;&acy;&dcy;&rcy;&acy;&tcy;

2.2. Усно розв’язати вправу 162 (1; 3; 5) (стор. 33 підручника).

ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ

Письмово виконати вправи з підручника (стор. 32 – 38):

Завдання 3.

148; 150 (2; 4); 160 (1; 3).

Завдання 4.

163 (2; 4); 172; 178.

ІІІ. Відпрацювання умінь розв’язування нестандартних вправ

Завдання 5.

190.

Готуємось до індивідуального опрацювання матеріалу

Виконай додавання:

Обчислити зручним способом:

Сашко зібрав 26 грибів, Василько – на 15 грибів більше, ніж Сашко, а Назар – на 28 грибів більше, ніж Сашко і Василько разом. Скільки грибів зібрали три хлопчики?
Першого дня на виставці побувало 475 відвідувачів, другого – на 47 більше, ніж першого, а третього – на 326 менше, ніж першого та другого дня разом. Скільки відвідувачів побувало на виставці за три дні?

Урок №8

«Бо що тільки людина посіє, та саме й пожне!»

Послання до галатів 6:7

Внутрішньопредметне узагальнення матеріалу

Натуральні числа. Додавання і віднімання натуральних чисел

І. Засвоєння термінології до теми

1. Повторити блок № 1.

2. Дати письмово відповідь на питання , запропоновані вчителем.

ІІ. Відпрацювання практичних умінь та навичок

Завдання 1.

Усно розв’яжи вправи:

Запиши цифрами число 5 мільйонів 14 тисяч 70.

А	Б	В	Г
5 140 070	5 140 007	5 014 070	014 007

Виконай додавання: 13 751+ 47 464

А	Б	В	Г
60 115	61 115	60 215	61215

Виконай віднімання: 14 139 – 8386.

А	Б	В	Г
5753	5853	6753	6853

Завдання 2.

Письмово розв’яжи вправи:

Обчисли суму, використовуючи властивості додавання:

2) .
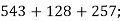
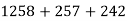
1. Обчисли зручним способом:

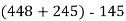; 2) .
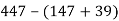1. Мотоцикл за першу годину проїхав 59 км, а за другу – на 12 км менше. Яку відстань проїхав мотоцикл за ці дві години?
2. Склади найменше і найбільше чотирицифрові числа із цифр 0; 8; 3 і 1 так, щоб у кожному числі всі цифри були різними.
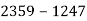
3. Як зміниться різниця , якщо зменшуване збільшити на 241, а від’ємник збільшити на 253?
4. У першій шафі стоїть 92 книги, у другій – на 24 книги менше, ніж у першій, а у третій стоїть стільки книг, скільки у першій і другій разом. Скільки книг стоїть у трьох шафах разом?
5. На клумбі росли троянди, айстри і жоржини. Всього 360 рослин. Троянди становлять половину всіх рослин, а айстри – третину троянд. Скільки жоржин росло на клумбі?

Тема №2. Множення і ділення натуральних чисел

Урок №1

Множення і ділення натуральних чисел

«З усіх утрат втрата часу найтяжча»

Григорій Сковорода

Питання

Множення натуральних чисел.
Властивості множення
Степінь натурального числа
Ділення натуральних чисел
Ділення з остачею

Література

Істер О. С. Математика: підручник для 5 класу. – §§ 5 – 9, стор. 41 – 69.

1.Множення натуральних чисел
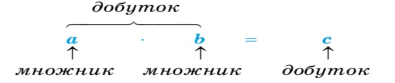
1.1	Добуток натуральних чисел означає суму, що складається з доданків, кожний з яких дорівнює .
1.2	Числа при множенні називаються так: $C:\Users\олеся\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\Нове зображення (5).bmp$
1.3	При множенні будь-якого числа на 1, одержуємо те ж саме число, яке множили: .
1.4	При множенні будь-якого числа на нуль, одержуємо нуль:
1.5	Щоб помножити натуральне число на розрядну одиницю (10, 100, 1000, …) , треба до числа приписати стільки нулів, скільки їх є в розрядній одиниці.
1.6	Перед буквеним виразом і перед дужками знак множення можна не писати.
2. Властивості множення
2.7	*Переставна властивість* Від перестановки множників добуток не змінюється, .
2.8	*Сполучна властивість* Щоб добуток двох чисел помножити на третє число, можна перше число помножити на добуток другого і третього чисел,
2.9	*Розподільна властивість* Щоб число помножити на суму двох чисел, можна це число помножити на кожний доданок і отримані добутки додати, Щоб число помножити на різницю двох чисел, можна це число помножити на зменшуване і від’ємник і знайдені добутки відняти,
3. Степінь натурального числа
3.10	Добуток, в якому всі множники рівні між собою, називають степенем. Основа степеня – це множник, який повторюється, показник степеня вказує скільки разів множник міститься у добутку.	3 – основа степеня 4 – показник степеня – степінь
3.11	Якщо в числовий вираз входить степінь, то спочатку виконується піднесення до степеня, а після цього інші дії.
4. Ділення натуральних чисел
4.12	Дія, за допомогою якої за добутком і одним із множників знаходять другий множник, називається діленням.
4.13	Числа при діленні називаються так: $C:\Users\олеся\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\Нове зображення (6).bmp$
4.14	На нуль ділити не можна!
4.15	Щоб поділити натуральне число, яке закінчується нулями, на розрядну одиницю, треба відкинути справа в цьому числі стільки нулів, скільки їх є в розрядній одиниці.
5. Ділення з остачею
5.16	Якщо одне число не ділиться націло на інше, то маємо ділення з остачею.
5.17	Остача завжди менша від дільника.
5.18	Щоб знайти ділене, треба дільник помножити на неповну частку і додати остачу.

ЗАПАМ’ЯТАЙ

2 ∙ 25 = 50

2 ∙ 50 = 100

4 ∙ 25 = 100

8 ∙ 125 = 1000

Урок №2

«Не буде ледачий пекти свого полову,

а людина трудяща набуде маєток цінний»

Книга приповістей Соломонових 12 : 27

Фронтальне опрацювання матеріалу

Множення натуральних чисел

І. Робота над засвоєнням понять, термінів і правил

Завдання 1.

Повторити тези 1.1 – 1.5 блоку № 2.
Усно відповісти на питання:

Що означає добуток натуральних чисел ?
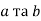
Як називаються числа при множенні?
Що отримуємо при множенні будь-якого числа на 1?
Що отримуємо при множенні будь-якого числа на 0?
Як помножити натуральне число на розрядну одиницю?

Завдання 2.

Усно розв’язати вправи, запропоновані учителем під час перегляду презентації.

ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ

Письмово виконати вправи з підручника (стор. 42 – 46):

Завдання 3.

200 (1, 3, 5); 203

Завдання 4.

208 (1); 211; 213; 215; 216.

ІІІ. Відпрацювання умінь розв’язування нестандартних вправ

Завдання 5.

222.

Уроки №3, 4

«Страх Господній – початок премудрості,

нерозумні погорджують мудрістю та напучуванням»

Книга приповістей Соломонових 1:7

Фронтальне опрацювання матеріалу

Властивості множення

І. Робота над засвоєнням понять, визначень, правил

Завдання 1.

Повторіть тези 1.1. – 2.9.
Усно дайте відповіді на питання:

Що означає добуток двох чисел?
Як називаються числа при множенні?
Що ми одержимо, якщо помножимо будь-яке число на 1?
Що ми одержимо, якщо помножимо будь-яке число на 0?
Як помножити число на одиницю з нулями?
Сформулюйте переставну властивість множення.
Сформулюйте сполучну властивість множення.
Сформулюйте розподільну властивість множення відносно суми.
Сформулюйте розподільну властивість множення відносно різниці.

Завдання 2.

Усно розв’язати вправи, запропоновані учителем під час перегляду презентації.

ІІ. Відпрацювання практичних умінь і навичок

Письмово виконати вправи (стор. 50 – 53):

Завдання 3.

227 (1; 3; 5); 229 (2; 4; 6).

Завдання 4.

4.1. Розглянути приклад 1, стор.49.

4.2. 231.

Завдання 5.

5.1. Розглянути приклад 2, стор. 49.

5.2. 233.

Завдання 6.

6.1. Розглянути приклад 3, стор. 49.

6.2. 235.

Завдання 7.

240; 242; 243 (1; 3); 245 (2; 4); 246 (1; 3).

ІІІ. Відпрацювання умінь розв’язування нестандартних задач

Завдання 8.

248; 250; 252.

Урок №5

«Я зроблю тебе мудрим, і буду навчати

тебе у дорозі, якою ти будеш ходити, Я

дам тобі раду, Моє око вважає на тебе!"
Псалом 31 :8

Фронтальне опрацювання матеріалу

Степінь натурального числа з натуральним показником

І. Робота над засвоєнням понять, термінів, правил

Завдання 1.

Повторити тези 1.1. – 3.11 блоку № 2.
Усно дайте відповіді на питання:

Сформулюйте переставну властивість множення.
Який вираз називають степенем? Наведіть приклад.
Як називаються числа при множенні?
Як помножити число на одиницю з нулями?
Сформулювати правило порядку дій у виразі, який містить степінь.

Завдання 2.

2.1. Обчисли: , , .

2.2. Усно виконати вправи з підручника (стор. 55 – 56): 255, 257, 259

ІІ. Відпрацювання умінь і навичок, застосування правил

Завдання 3.

3.1. Розглянути приклади 1 та 2 на стор. 54 – 55 підручника.

3.2. Виконати з підручника, стор. 56 – 57, наступні вправи: 264, 266, 268, 272, 274.

ІІІ. Відпрацювання умінь і навичок розв’язування нестандартних задач

Завдання 4.

Виконати письмово вправи з підручника, стор. 57: 278, 280.

Готуємось до індивідуального опрацювання матеріалу

Виконайте множення:

Виконайте дії:
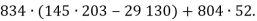
Виконай вправу 212 ст. 44.
Виконай вправу 245 (1, 3) ст. 52.

Уроки №7, 8

І все, що тільки чините, робіть

від душі, немов Господеві, а не людям!

Послання до колосян 3:23

Фронтальне опрацювання матеріалу

Ділення натуральних чисел

І. Робота над засвоєнням термінів, понять і правил

Завдання 1.

Повторіть тези 1.1. – 4.13 і дайте відповіді на питання:

Як називаються числа при множенні?
Як називаються числа при діленні?
За допомогою якої дії знаходять невідомий множник?
На яке число ділити не можна? Поясни чому.
Як називається число, на яке ділять?

ІІ. Відпрацювання умінь і навичок, застосування правил

Завдання 2.

2.1. Обчислити усно:

32 – 15 81 · 6 48 : 3

96 – 38 9 · 16 340 : 2

58 + 42 63 · 3 804 : 4

2.2. Знак якої арифметичної дії треба поставити замість зірочки, щоб була

правильною рівність:

45 * 1 = 45

2 * 2 = 4

85 * 0 = 85

28 * 0 = 0

2.3. Чому дорівнює значення виразу, де а – деяке відмінне від нуля число:

а : 1 + 0 : а

а · 1 – а : 1

(а · 1 – 1) · 0

Завдання 3.

Знайдіть значення числового виразу найзручнішим способом:

а) 25 · 79 · 4; б) 43 · 89 + 89 · 57.

Виконай вправи з підручника, стор. 60 – 62: 289, 291, 294, 298, 301, 305
З одного порту в протилежних напрямках одночасно вийшли пароплав зі швидкістю 25 км/год і катер зі швидкістю 32 км/год. Яка відстань буде між ними через 3 год після початку руху?

ІІІ. Відпрацювання умінь і навичок розв’язування нестандартних задач і вправ

Завдання 4.

У вірші

Кмітливі труднощі долають,

Вони завжди перемагають.

А винахідливі завжди

Сухими вийдуть із води.

Важких завдань для нас немає

Сьогодні ми перемагаєм.

порахуйте кількість букв у перших двох рядках і розділіть їх на кількість слів у вірші.

Урок №9

«Трава засихає, а квітка зів’яне,

Слово ж нашого Бога повіки стоятиме!»

Ісаї 40:8

Фронтальне опрацювання матеріалу

Ділення з остачею

І. Робота над засвоєнням термінів, понять і правил

Завдання 1.

Повторіть тези блоку №2 і дайте відповіді на питання:

При множенні будь-якого числа на нуль одержуємо …
Коли ми маємо ділення з остачею?
Як називаються числа при діленні?
Що більше: остача чи дільник?
Як знайти ділене при діленні з остачею?

Завдання 2.

Обчислити приклади й за кодом розшифрувати слово.

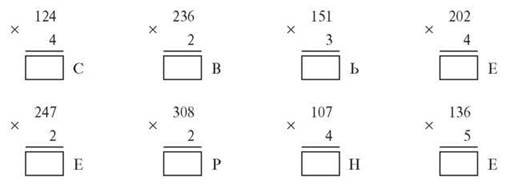
472	494	616	808	496	680	428	453

ІІ. Відпрацювання умінь і навичок розв’язування вправ, застосування правил

Завдання 3.

Виконай вправи з підручника (стор.65 – 66): 315, 317, 321, 323, 324.

Готуємось до індивідуального опрацювання матеріалу

Знайдіть ділене, якщо:

дільник дорівнює 14, неповна частка – 4, а остача – 3.
дільник дорівнює 14, неповна частка – 5, а остача – 12.

Виконайте дії:

За 8 год автомобіль проїхав 528 км. Скільки кілометрів проїде він, рухаючись з цією самою швидкістю, за 10 год?
Виконайте вправу 298 ст. 61.

Урок №11

«Ледача рука до убозтва

веде, рука ж роботяща збагачує»

Книга приповістей Соломонових 10 : 4

Внутрішньопредметне узагальнення матеріалу

Множення і ділення натуральних чисел

І. Засвоєння термінології до теми

1. Повторити блок № 2.

2. Дати письмово відповідь на питання, запропоновані вчителем.

ІІ. Відпрацювання практичних умінь та навичок

Завдання 1.

Усно розв’яжи вправи:

У запису число 5 – це:

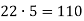
А	Б	В	Г
Множник	Добуток	Доданок	Дільник

Обчислити значення виразу: .

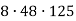
А	Б	В	Г
480	4800	48000	480000

Остача при діленні дорівнює:

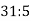
А	Б	В	Г
3	5	1	2

Завдання 2.

Письмово розв’яжи вправи:

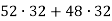
Знайди значення виразу , користуючись розподільною властивістю множення.
Обчисли: .
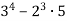Знайди значення виразу: 1) 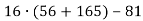; 2).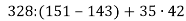
Автомобіль долає відстань у 480 км за 6 год. За скільки годин він подолає цю відстань, якщо зменшить швидкість на 20 км/год?
Щоб доїхати до санаторію, треба 5 годин їхати на потязі та 3 години – на автобусі. Який шлях треба подолати, щоб доїхати до санаторію, якщо швидкість потяга 75 км/год, а швидкість автобуса – 60 км/год?
За 12 днів треба було виготовити 156 іграшок, але кожного дня виготовляли понад план 13 іграшок. За скільки днів виконали план?

Тема №3. Числові та буквені вирази. Формули. Рівняння

Урок №1

Числові та буквені вирази. Формули. Рівняння

Даремно говорити,

що ви довіряєте Ісусу,

якщо ви не слідуєте Його порадам

К. Льюіс

Питання

Числові вирази. Буквені вирази і їх значення. Формули.
Рівняння.
Текстові задачі.

Література: Істер О.С. Математика: підручник для 5 класу. – §§ 10 – 13, ст. 69 – 105

Числові вирази. Буквені вирази та їх значення. Формули
1.1.	Вирази, які складаються із чисел, знаків дій і дужок, називаються числовими виразами.
1.2.	Якщо виконати дії в числових виразах, то отримаємо число, яке називається значенням числового виразу.
1.3.	Вираз, який містить букви, числа, знаки дій і дужки, називають буквеним виразом.
1.4.	Формула – це запис деякого правила за допомогою букв, що встановлює взаємозв’язок між величинами.	S – площа прямокутника, – його сторони
Рівняння
2.5.	Рівність, що містить невідоме число, називається рівнянням.
2.6.	Значення невідомого, при якому рівняння перетворюється у правильну числову рівність, називається розв’язком або коренем рівняння.
2.7.	Щоб знайти невідомий доданок, треба від суми відняти відомий доданок
2.8.	Щоб знайти невідоме зменшуване, треба до різниці додати від’ємник.
2.9.	Щоб знайти невідомий від’ємник, треба від зменшуваного відняти різницю.
2.10.	Щоб знайти невідомий множник, треба добуток поділити на відомий множник.
2.11.	Щоб знайти невідоме ділене, треба частку помножити на дільник.
2.12.	Щоб знайти невідомий дільник, треба ділене поділити на частку.
Текстові задачі
3.13.	Задачі на рух. Формула шляху , - відстань, - швидкість, - час.
3.14.	Задачі, пов’язані з вартістю товару. Вартість товару дорівнює ціні, помноженій на кількість товару , - вартість товару, - ціна 1 одиниці товару, - кількість товару
3.15.	Задачі на роботу Робота дорівнює продуктивності помноженій на час роботи. , - робота, - продуктивність праці, - час роботи

Урок №2

Математика – дивовижна вчителька в

мистецтві спрямовувати думки, наводити

порядок там, де вони не впорядковані,

фільтрувати брудне й наводити ясність.

Ж. Фабр

Фронтальне опрацювання матеріалу

Числові і буквені вирази. Формули

І. Робота над засвоєнням понять, термінів, формул

Завдання 1.

Повторити 1.1 – 1.4 блоку №3.

1.2. Доповнити речення:

1) Числовим виразом називається ________________________________________________

2) Значенням числового виразу називається _______________________________________

3) Буквеним виразом називається ________________________________________________

4) Для розв’язання подібних задач використовується ________________________________

ІІ. Відпрацювання умінь і навичок, застосування правил

Завдання 2.

2.1. Обчисліть:

1) 75 + (25 + 13); 3) 75 – (25 + 13);

2) (36 + 19) – 19; 4) 25 + 18 + 35 + 52.

2.2. Закінчити запис властивостей:

1) a + (b + c)=_________; 3) _________=(a – b) – c;

2) (a + b) – c=_________; 4) a + b=__________.

?! Коли використовуються властивості додавання та віднімання?

Завдання 3.

Який із числових виразів має значення 18:

а) 22 – (6+2); б) 22 +(6–2); в) 22 – (6–2); г) 22+(6+2).

Завдання 4.

Запишіть вираз і знайдіть його значення при зазначених числах:

1) різниця х і 15, якщо х =21

2) сума 2 і у , якщо у =19

3) Андрійко купив 14 конвертів по а коп., та b марок по 80 коп. На скільки більше заплатив хлопчик за марки ніж за конверти( а =12, b= 7).

Завдання 5.

Знайдіть значення виразу:

1) (43 – b) 15, якщо b =28.

2) ( х – 238) у ,якщо х =16876, у =47.

Завдання 6.

Використовуючи формулу шляху ( s = vt), знайдіть:

1) значення шляху s ( у км ), якщо v =60 км/год, t =2 год;

2) значення швидкості v (у м/хв), якщо s =180 м, t =12 хв;

ІІ. Відпрацювання умінь і навичок розв’язування нестандартних задач

Завдання 7.

Знайдіть периметри

1) квадрата, якщо його сторона 4 см.

2) прямокутника, якщо ширина 6 см та довжина 5 см

Завдання 8.

Обчисліть значення у за формулою , якщо

Уроки №3, 4

«Серце розумне знання набуває,

і вухо премудрих шукає знання»

Книга приповістей

Соломонових 18 : 15

Фронтальне опрацювання матеріалу

Рівняння

І. Робота над засвоєнням понять, термінів, правил

Завдання 1.

Повторити тези 1.1 – 2.12 блоку № 3.
Усно відповісти на питання:

Що називається рівнянням?
Як знайти невідомий доданок?
Як знайти невідоме зменшуване?
Як знайти невідомий від’ємник?
Як знайти невідомий множник?
Як знайти невідоме ділене?
Як знайти невідомий дільник?

Завдання 2.

Усно розв’язати вправи, запропоновані учителем під час перегляду презентації.

ІІ. Відпрацювання умінь і навичок, застосування правил

Завдання 3.

Користуючись правилами розв’язування рівнянь, виконати вправи з підручника, стор. 79:

368 (1; 3); 372; 374 (2; 4; 6); 384.

Завдання 4.

Розглянь приклад 3 на стор. 78 підручника. Виконай вправу (стор. 79) 377 (2; 4).

Завдання 5.

Розглянь приклад 1 на стор. 78 підручника. Виконай вправи (стор. 86) 386 (1; 3; 5); 388 (1).

Завдання 6.

Розглянь приклад 4 на стор. 78 підручника. Виконай вправу (стор. 82) 391 (2; 4; 6).

Завдання 7.

Розглянь приклад 2 на стор. 78 підручника. Виконай вправу (стор. 82) 395 (1; 2).

ІІІ. Відпрацювання умінь розв’язування нестандартних вправ

Завдання 8.

Виконай вправи, стор.83: 399; 404.

Готуємось до індивідуального опрацювання матеріалу

Обчислити значення виразу , якщо .
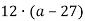
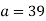
Розв’язати рівняння:

Розв’язати рівняння:

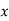
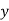
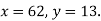
У вагоні трамвая було пасажирів. На зупинці з нього вийшло 24 пасажири, а ввійшло – . Скільки пасажирів стало у вагоні? Обчисліть значення отриманого виразу, якщо
Записати формулу для знаходження площі прямокутника і знайти її значення, якщо його сторони дорівнюють 3 см і 7 см.

Уроки №6, 7

«Без бажання все важке, навіть найлегше»

Григорій Сковорода

Фронтальне опрацювання матеріалу

Розв’язування текстових задач

І. Робота над засвоєнням понять, термінів, правил

Завдання 1.

Повторити тези 3.13 – 3.15 блоку № 3.
Прочитати §12 підручника (стор. 84 – 90).
Усно відповісти на питання:

Як знайти відстань, якщо відома швидкість і час?
Що таке продуктивність праці?
Як знайти виконану роботу, якщо відомі продуктивність праці і час роботи?
Як знайти швидкість, якщо відомі відстань і час?
Як знайти вартість, якщо відомі ціна товару і його кількість?
Що називається швидкістю відділення і швидкістю віддалення?
Які види задач вам відомі?

ІІ. Відпрацювання умінь та навичок, застосування правил

Завдання 2.

Використовуючи матеріалу блоку, підручника виконайте письмово вправи:

409, 410, 413, 416, 420, 423, 425, 427(1), 436, 441, 445.

ІІІ. Відпрацювання умінь і навичок розв’язування нестандартних задач

Завдання 3.

На день народження Фрекен Бок спекла торт. Малюк і торт важили стільки ж, скільки Карлсон і Фрекен Бок. Коли торт з’їли, Карлсон важив стільки, скільки Фрекен Бок і Малюк. Довести, що Карлсон з’їв шматок торта, що важив стільки, скільки Фрекен Бок до дня народження.

Урок №8

«Найкраща помилка та, якої допускаються у навчанні»

Григорій Сковорода

Фронтальне опрацювання матеріалу

Розв’язування текстових задач за допомогою рівнянь

І. Робота над засвоєнням понять, термінів, правил

Завдання 1.

Повторіть блок №3 і дайте відповіді на питання кросворду:

ІІ. Відпрацювання практичних умінь та навичок

Завдання 2.

Розглянути приклади розв’язування задач за допомогою рівнянь на стор. 100 підручника.

Завдання 3.

Користуючись розглянутими зразками, виконайте вправи з підручника, стор.101 – 102: 453; 455; 460, 462.

Готуємось до індивідуального опрацювання матеріалу

Виконайте вправу 429 ст. 96.
Шафа, ліжко та меблева стінка разом коштують 3927 грн. Вартість ліжка в 2 рази більша за вартість шафи, а вартість меблевої стінки у 8 разів більша за вартість шафи. Знайдіть вартість шафи, ліжка та меблевої стінки окремо.
Майстер виготовляє 120 деталей за 8 год, а кожен з двох його учнів – по 36 деталей за 4 год. За скільки годин вони утрьох виготовлять 198 деталей?

Урок №10

«Ледача рука до убозтва

веде, рука ж роботяща збагачує»

Книга приповістей Соломонових 10:4

Внутрішньопредметне узагальнення матеріалу

Числові і буквені вирази. Формули. Рівняння

І. Засвоєння термінології до теми

1. Повтори блок № 3.

2. Дай письмово відповіді на питання, запропоновані вчителем.

ІІ. Відпрацювання практичних умінь та навичок

Завдання 1.

Усно виконати вправи:

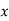
Оля зібрала кг огірків, а її мама – на 6 кг більше. Скільки всього огірків забрала Оля з мамою?

А	Б	В	Г

Знайти корінь рівняння .

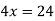
А	Б	В	Г

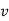
Олег іде берегом річки зі швидкістю км/год, а Ігор пливе у човні зі швидкістю у 2 рази більшою. З якою швидкість пливе Ігор у човні?

А	Б	В	Г

Завдання 2.

Письмово розв’яжи вправи:

Знайдіть значення виразу , якщо .
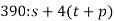
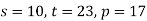
Розв’яжіть рівняння .
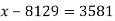
Розв’яжіть рівняння .

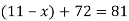Знайдіть значення виразів. Встановіть відповідність між виразом (1 – 4) та його значенням (а – г):

1) ;

2) ;

3) ;

4) .

а) 89

б) 5

в) 11

г) 3

Потяг рухається зі швидкістю 60 км/год, долає деяку відстань за 5 год. За скільки годин подолає таку саму відстань, якщо зменшить швидкість на 10 км/год?
Розв’язати задачу за допомогою рівняння: Різниця двох чисел дорівнює 540. Знайди ці числа, якщо одне з них утричі більше за друге.

Тема №4. Відрізок, площина, пряма, промінь. Шкала. Координатний промінь

Урок №1

Відрізок, промінь пряма. Шкала. Координатний промінь

«Знання збираються по краплині, як вода в долоні»

Прислів’я

Питання

Приклади та задачі на всі дії з натуральними числами.
Відрізок та його довжина.
Промінь, пряма.
Координатний промінь, шкала.

Література

Істер О.С. Математика: підручник для 5 класу. – §§ 15 – 18, ст. 115 – 140

1. Приклади та задачі на всі дії з натуральними числами
1.1.	У виразах з дужками спочатку обчислюється значення виразів у дужках
1.2.	У виразах без дужок спочатку обчислюється піднесення до степеня, потім по порядку зліва направо множення і ділення, а потім додавання і віднімання.
2. Відрізок та його довжина
2.3.	Будь-які дві точки можна сполучити лише одним відрізком.	АВ - відрізок
2.4.	Два відрізки називаються рівними, якщо їхні довжини однакові.
3. Промінь, пряма
3.5.	Якщо продовжити відрізок АВ за його кінець В необмежено, то одержимо промінь АВ.	А – початок променя. Кінця у променя немає.
3.6.	Якщо продовжити відрізок АВ у дві сторони, то отримаємо пряму. А В	АВ – пряма. Пряма не має ні початку, ні кінця.
3.7.	Через будь-які дві точки можна провести пряму і до того ж тільки одну.
4. Координатний промінь. Шкала
4.8.	Координатний промінь – це промінь із заданою точкою відліку та одиничним відрізком.
4.9.	Число, яке відповідає точці на координатному промені, називається координатою точки.	К (1); L (6)
4.10.	Якщо координатний промінь спрямований зліва направо, то з двох натуральних чисел більшому відповідає точка, яка лежить праворуч, а меншому — ліворуч.	1 < 6 К – лівіше, L – правіше
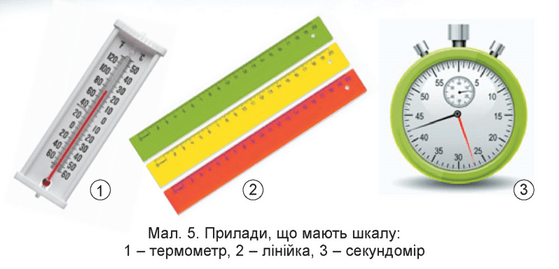
4.11	Систему поділок разом з відповідними числами називають шкалою.

Урок №2

«Я все можу в Тім, Хто

мене підкріпляє, – в Ісусі Христі»

Послання ап. Павла до филипʼян 4:13

Фронтальне опрацювання матеріалу

Вправи та задачі на всі дії з натуральними числами

І. Робота над засвоєнням понять, термінів, правил

Завдання 1.

Повторити тези 1.1, 1.2 блоку № 4.
Усно відповісти на питання:

Який порядок виконання дій у виразі з дужками?
Який порядок виконання дій у виразі без дужок?

ІІ. Відпрацювання практичних умінь та навичок

Завдання 2.

2.1. Прочитайте Буття 4:26, 5:3, 6. Знайдіть рік, коли люди почали призивати Ім’я Господнє.

2.2. Прочитайте Буття 1:31, 2:2. Порахуйте, за скільки годин Бог створив світ.

2.3. Прочитайте Буття 6:13 – 17. Випишіть значення чотирьох вимірів ковчега: кількість поверхів, довжина, ширина і висота.

2.4. Древні євреї користувалася мірою довжини 1 лікоть, що становив або 40 см (малий лікоть), або 48 см. Ми будемо користуватись ліктем у 48 см. Знайдіть:

1) довжину, ширину і висоту ковчега у метрах;

2) висоту одного поверху ковчега в ліктях та метрах.

2.5. Прочитайте Буття 7:1 – 24. Знайдіть:

1) скільки років було Ноєві, коли розпочався потоп (Бут. 7:6)?

2) через скільки днів, відколи Ной зайшов у ковчег, почався потоп (Бут 7:4, 10)?

3) скільки днів йшов дощ (Бут. 7:4, 12, 17)?

4) скільки людей було у ковчезі (Бут. 7:13)?

Завдання 3.

Прочитайте Буття 6:14 – 22.Знайдіть:

Скільки в ковчезі було вікон і дверей (Бут. 6:16)?
Який розмір мало одне вікно (Бут 6:16)?
1. Прочитайте Буття 7:10 – 24. Знайдіть:

Скільки днів прибувала вода (Буття 7:24)?
Скільки це місяців?
1. Прочитайте Буття 8:5 – 16. Знайдіть скільки років виповнилось Ною, коли закінчився потоп (Буття 8:13)?
2. Прочитайте Буття 1:1 – 10, 2:5 – 6, 2:10 – 14. Знайдіть:

Скільки було материків, морів, річок і океанів?
Як зволожувалась земля?

Завдання 4.

Прочитайте 2 Петра 3:5 – 6.

З чого були складені небеса й земля?
Куди поділась вода потопу?
1. Прочитайте Йова 40:15 – 32, 41:1 – 26. Знайдіть:

Дві назви динозаврів;
Чи змогли динозаври вміститись у ковчезі?

Готуємось до індивідуального опрацювання матеріалу

Знайди значення виразу .
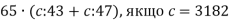Знайди значення виразу:

2) .

На чотирьох автостоянках знаходиться 347 машин. На першій автостоянці 85 машин, що на 23 машини менше, ніж на четвертій. На другій та третій автостоянках машин порівну. Скільки машин на другій автостоянці?

Урок №4

«Справжній скарб для

людини – вміння трудитися»

Езоп

Фронтальне опрацювання матеріалу

Відрізок і його довжина

І. Робота над засвоєнням понять, термінів, правил

Завдання 1.

Повторіть тези 2.3 – 2.4 блоку № 4.
Усно дайте відповідь на питання:

Як отримати відрізок?
Які два відрізки називають рівними?
Які ви знаєте міри довжини?
Скільки сантиметрів у дециметрі?

Завдання 2.

Прочитай казку про точку і відрізок, встав пропущене слово:

Жила собі Точка. Вона була дуже цікава і хотіла все знати. Побачить незнайому лінію і неодмінно запитає: - Як ця лінія називається? Довга вона чи коротка?

Подумала одного разу Точка, щоб більше знати, потрібно подорожувати і вирушила у подорож. Вийшла Точка на Пряму і пішла по ній. Довго йшла. Стомилася. Зупинилася і говорить:- Чи довго мені ще йти? Чи скоро кінець Прямої ? Засміялася Пряма.

Тоді я поверну назад ,- сказала Точка. Я пішла, мабуть, не в той бік. Засмутилася Точка: Як же мені бути? Що ж мені доведеться отак іти без кінця?

Пожаліла Пряма Точку і покликала Ножиці. Клацнули вони перед носом Точки і розрізали Пряму. Точка зраділа і попросила Ножиці клацнути ще й з другого боку. Ножиці виконали прохання Точки .

Чудово!- закричала Точка. - Що ж це вийшло? З одного боку кінець і з другого?

- Це…_________.

Кінець форми ІІ. Відпрацювання практичних умінь та навичок

Завдання 3.

Виконай усно вправу 551, стор. 122 підручника.

Завдання 4.

Виконай письмово вправи, стор.123 – 124 підручника:

559, 560, 562, 566, 568.

ІІІ. Відпрацювання умінь розв’язування нестандартних вправ

Завдання 5.

5.1. Розглянь розв’язування вправи 571, стор.125 підручника.

5.2. Скориставшись розглянутим прикладом, виконай вправи, стор. 125; 572, 573.

Урок №5

«Добре засвоєна

мудрість не забувається ніколи»

Піфагор

Фронтальне опрацювання матеріалу

Промінь, пряма, площина

І. Робота над засвоєнням понять, термінів і правил

Завдання 1.

Повторіть тези 2.3 – 3.7 блоку №4.
Усно дайте відповіді на питання:

Як утворюється відрізок?
Маємо відрізок МР. Як утворити промінь МР?
Чи має пряма початок і кінець?
Скільки прямих можна провести через точки ?

Завдання 2.

Пряма зображена на рисунку:

ІІ. Відпрацювання практичних умінь і навичок із застосування правил

Завдання 3.

На сторінці 128 у тексті §17 знайти відповідь на питання: «Які промені називаються доповняльними?»
Виконай усно вправи, стор. 128 – 129 підручника: 579, 583, 589

Завдання 4.

Виконай письмово вправи, стор. 128 – 129 підручника: 585, 587, 591, 593.

ІІІ. Відпрацювання умінь і навичок розв’язування нестандартних задач

Завдання 5.

Виконай письмово вправу 599, стор. 130 підручника.

Урок №6

«Не досить оволодіти премудрістю,

потрібно також вміти користуватися нею»

Народне прислів’я

Фронтальне опрацювання матеріалу

Координатний промінь. Шкала

І. Робота над засвоєнням понять, термінів і правил

Завдання 1.

Повторіть тези блоку 4.8 – 4.11 блоку № 4.
Усно дайте відповіді на питання:

Що називається відрізком?
Які одиниці вимірювання довжини відрізка ви знаєте?
Чим відрізняється пряма від відрізка?
Скільки прямих можна провести через 2 точки?
Що називають променем? Чим він відрізняється від відрізка і прямої?
Що таке координатний промінь?
Що називається координатою точки?
Як порівняти числа за допомогою координатного променя?
Які ви знаєте прилади, у яких є шкала?

Завдання 2.

Виконайте усно:

Яким числам відповідають точки А, В, С, D на рисунку?

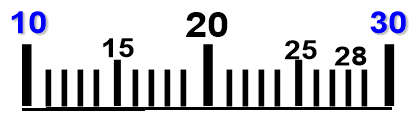
В А D С

Яку довжину має відрізок АВ?

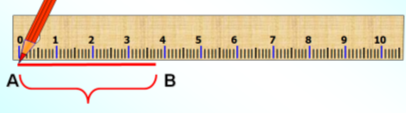
Усно виконай вправу 609, стор. 133

ІІ. Відпрацювання умінь і навичок, застосування правил

Завдання 3.

Накресли координатний промінь і познач на ньому числа 2, 3, 6, 9, 10, якщо одиничний відрізок дорівнює 1 см.
Виконай вправи з підручника, стор. 134 – 136: 611, 613, 618, 623, 627, 631.

ІІІ. Відпрацювання умінь і навичок розв’язування нестандартних задач

Завдання 4.

Коник стрибунець за один стрибок переміщається вздовж координатного променя вправо на 5 одиничних відрізків або вліво – на 3 одиничних відрізки. Чи зможе він за декілька стрибків із точки О (0) потрапити в точку А (7)?

Готуємось до індивідуального опрацювання матеріалу

Накресли промінь з початком у точці С. Познач на ньому довільну точку К. Відклади на промені відрізок СА = 5 см. Виміряй і запиши довжину відрізка КА.
Накресли координатний промінь. За одиничний відрізок візьми одну клітинку. Познач на ньому точки А (0), К(1), М (11), N (7).
Точка М належить відрізку АВ. Знайдіть довжину відрізка АВ, якщо АМ = 42 см, ВМ = 68 см.
На координатному промені відміть числа 200, 240, 320, 360.

Урок №8

«Як приємно дізнатись,

що ти чогось навчився»

Жан Мольєр, французький письменник

Внутрішньопредметне узагальнення матеріалу

Відрізок, пряма, промінь. Координатний промінь

І. Систематизація та узагальнення теоретичних знань

Завдання 1.

Повтори блок № 4.
Дай письмово відповідь на питання , запропоновані вчителем.

Завдання 2.

Усно виконай вправи, запропоновані вчителем (презентація).
Знайди значення виразу .

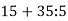
А	Б	В	Г
25	22	11	10

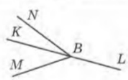
Серед променів, зображених на малюнку, знайди пару доповняльних

А	Б	В	Г

Якому числу відповідає точка D на малюнку

А	Б	В	Г
3	4	5	6

ІІ. Систематизація та узагальнення практичних умінь та навичок

Завдання 3.

Письмово виконай вправи:

На відрізку АМ, довжина якого 30 см, позначено точки В і С так, що АВ = 7 см, МС = 13 см. Знайди довжину відрізка ВС.
Накресли координатний промінь і познач на ньому точки C (3), D (10), L(5), N(8).
Знайди ціну поділки шкали, якщо між числами 20 і 80 міститься 6 поділок.
Знайди значення виразу:
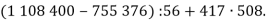
На координатному промені відміть числа 100; 120; 150; 200.
Точка К належить відрізку CD. Знайди довжину відрізка CD, якщо CK = 39 см, DK = 64 см.

Тема №5. Кути. Многокутники

Урок №1

Кути. Многокутники

«Міцні знання – гарантія успіху»

Прислів’я

Питання

Кут. Види кутів
Величина кута. Вимірювання і побудова кутів
Многокутник та його периметр.
Трикутник.

Література

Істер О.С. Математика: підручник для 5 класу. – §§ 19 – 21, ст. 140 – 164.

1. Кут. Види кутів
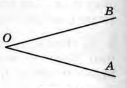
1.1	Кут – це геометрична фігура, утворена двома променями, що виходять з однієї точки. Промені ОВ і ОА називаються *сторонами* кута, точка О – *вершина* кута. Позначається .
1.2	Кути називаються рівними між собою, якщо їх можна накласти один на одного і вони збігаються.
1.3	Якщо сторонами кута є доповняльні промені, то такий кут називається розгорнутим.
1.4	Кут, удвічі менший від розгорнутого, називається прямим.
1.5	Кут, який менший від прямого кута, називається гострим.
1.6	Кут, який більший за прямий кут, але менший від розгорнутого, називається тупим.
2. Величина кута. Вимірювання і побудова кутів
2.7	Кути вимірюють у градусах. Позначають: .
2.8	Градусна міра розгорнутого кута – 180, прямого кута – 90 .
2.9	Прилад, за допомогою якого вимірюють градусну міру кутів, називається транспортиром.
2.10	Промінь, який виходить із вершини кута і розбиває його на два рівні кути, називається бісектрисою кута.
3. Многокутник та його периметр
3.11	Ламана — це фігура, яка складається з певної кількості точок і відрізків, що послідовно їх сполучають. Точки називаються вершинами ламаної, а відрізки — ланками ламаної.
3.12	Якщо початок ламаної збігається з її кінцем, то така ламана називається замкненою.
3.13	Замкнену ламану називають многокутником, її ланки називають *сторонами* многокутника, а вершини – *вершинами* многокутника.
3.14	Суму довжин усіх сторін многокутника називають його периметром.
4. Трикутник
4.15	Многокутник, який має три сторони називається трикутником.
4.16	Якщо в трикутнику дві сторони рівні між собою, то він називається рівнобедреним.
4.17	Якщо у трикутнику всі сторони рівні, то він називається рівностороннім.
4.18	Якщо у трикутнику немає рівних сторін, то він називається різностороннім.
4.19	Сума будь-яких двох сторін трикутника більша за третю сторону.
4.20	В залежності від величини кутів, трикутники поділяються на: гострокутні (всі кути гострі) прямокутні (один кут прямий) тупокутні (один кут тупий)
4.21	Сума всіх кутів трикутника дорівнює 180º.

Урок №2

«Не досить оволодіти премудрістю,

потрібно також вміти користуватися нею»

Народне прислів’я

Фронтальне опрацювання матеріалу

Кут. Види кутів

І. Робота над засвоєнням понять, термінів і правил

Завдання 1.

Повторіть тези блоку 1.1 – 1.6 блоку № 5.
Усно дайте відповіді на питання:

Що називається кутом?
Які кути називаються рівними?
Які є види кутів?
Який кут називається розгорнутим?
Який кут називається прямим?
Який кут називається гострим?
Який кут називається тупим?

Завдання 2.

2.1. Усно розв’яжи вправу 659, стор. 145.

2.2. Усно розв’язати вправу.

Який кут (розгорнутий, прямий, гострий, тупий) утворюють стрілки годинника, якщо вони показують:

5 годин;
10 годин 10 хвилин;
11 годин 5 хвилин;
3 години;
6 годин?

ІІ. Відпрацювання умінь і навичок, застосування правил

Завдання 3.

Виконайте письмово вправи, стор. 142 – 146: 638, 641, 649, 653, 657, 662.

ІІІ. Відпрацювання умінь і навичок розв’язування нестандартних задач

Завдання 4.

4.1. Одне яйце варять 5 хвилин. Скільки хвилин треба варити 5 яєць?

4.2. Іринка і Наталка однакового зросту. Наталка вища від Олі, а Тетянка вища ніж Іри. Хто вищий, Тетянка чи Оля?

Урок №3

«Єдиний шлях, що веде до знань – діяльність»

Бернард Шоу

Фронтальне опрацювання матеріалу

Величина кута, вимірювання та побудова кутів

І. Робота над засвоєнням понять, термінів і правил

Завдання 1.

Повтори тези 1.1 – 2.10 блоку № 5.
Дай відповіді на питання-загадки:

1) З двох променів складається,

Далеко простягається.

В загадках є і там, і тут,

А називається він ..

2) Як довідатись мені:

Є цей кут прямим чи ні?

Допоможе тут в момент

Цей чудовий інструмент.

Це прямих кутів супутник

Називається він…

3) Якщо в руки кутник взяти,

Більший кут обмалювати.

Вийде результат такий:

Кут дістанемо …

4) Як назвати кут такий,

Що є меншим, ніж прямий?

Відгадати дуже просто:

Називається він …

5) Гострий кут він переріс,

До тупого не доріс.

Як відомо, кут такий

Називається …

6) Щоб кути намалювати,

Нам його потрібно мати.

Як вимірюєш кути,

Кращий прилад не знайти.

Всім кутам він командир – Помічник наш …

7) Ця точка горда та щаслива,

Бо роль у неї особлива:

Вона куту ім’я дає,

Його сторін початком є.

Ця точка для кута єдина

І називається …

8) Щоб кути побудувати,

Транспортир нам треба мати,

А як цей будуєш кут,

І лінійки досить тут.

9) Кут прямий потрібно нам

Поділити пополам.

Кут одержимо новий,

А за видом він …

ІІ. Відпрацювання умінь і навичок, застосування правил

Завдання 2.

Виконай усно вправи, стор. 150 – 151: 667, 668, 670, 672.

Завдання 3.

За допомогою малюнків 104 – 107, стор. 147 – 148, та презентації вчителя вивчи правила користування транспортиром для вимірювання та побудови кутів.
За допомогою правил користування транспортиром, виконай письмово вправи, стор. 151 – 152: 673, 678.
Виконай письмово вправи, стор. 152 – 155: 681, 686, 696, 698 (1, 3).

ІІІ. Відпрацювання умінь і навичок розв’язування нестандартних задач

Завдання 4.

Виконай вправу 703, стор. 155.
Назви, будь ласка, де кути зустрічаються в нашому житті?

Автор девізу уроку

Бернард Шоу

англ. George Bernard Shaw

George Bernard Shaw 1925.jpg

Дата народження	26 липня 1856
Місце народження	Дублін
Дата смерті	2 листопада 1950 (94 роки)
Місце смерті	Ейот-Сент-Лоренс, Англія
Національність	Ірландець
Громадянство	Велика Британія
Рід діяльності	драматург і публіцист
Премії	Нобелівська премія з літератури (1925)
Автограф:

Урок №4

«Загублений той час,

який ти не використав на навчання»

Пліній, історик Стародавнього Риму

Фронтальне опрацювання матеріалу

Многокутник та його периметр. Трикутник. Види трикутників

І. Робота над засвоєнням понять, термінів і правил

Завдання 1.

Повтори тези 3.11 – 4.21 блоку № 5.
Усно дай відповіді на питання:

Що називають ламаною?
Дай визначення многокутника.
Назви елементи многокутника.
Що називаються периметром многокутника?
Що називають трикутником?
Які види трикутників в залежності від сторін ти знаєш?
Назви види трикутників в залежності від кутів.
Яку властивість мають сторони трикутника?
Яку властивість мають кути трикутника?

Завдання 2.

Усно розв’язати вправи:

716, стор. 160.
Знайди периметр трикутників зі сторонами: 1) 3 см, 4 см, 5 см; 2) 6 см, 6 см, 6 см; 3) 5 см, 5 см, 8 см. Вкажи вид трикутників за сторонами.
Визнач вид трикутника за його кутами: 1) 34^о; 127^о; 19^о; 2) 40^о; 50^о; 90; 3) 45^о; 60^о; 75º; 4) 95^о; 80^о; 5º.
Чи існує трикутник зі сторонами: 1) 3 см; 3 см; 5 см; 2) 5 дм; 2 дм; 2 дм; 3) 7 м; 9 м; 2 м.

ІІ. Відпрацювання умінь і навичок, застосування правил

Завдання 4.

Виконай письмово вправи, стор. 160 – 162: 719, 724, 726, 731, 736.

ІІІ. Відпрацювання умінь і навичок розв’язування нестандартних задач

Завдання 5.

Виконай письмово вправи, стор. 163: 743; 745; 746.
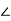
Накресліть трикутник АКN так, щоб А = 110^о . Виміряйте і запишіть градусні міри інших кутів трикутника. Визначте вид трикутника.

Готуємось до індивідуального опрацювання матеріалу

За допомогою транспортира побудуй кут АВС, градусна міра якого дорівнює:

За даним малюнком знайди градусну міру кута :

Одна сторона трикутника дорівнює 24 см, друга – в 3 рази більша за першу, а третя – на 16 см менша від другої. Знайди периметр трикутника.
Одна сторона трикутника на 14 см менша від другої і в 2 рази менша від третьої. Знайди сторони трикутника, якщо його периметр дорівнює 122 дм.

Урок №6

«Брешуть тільки одні негідники»

Ф.М. Достоєвський

Внутрішньопредметне узагальнення матеріалу

Кути. Многокутники

І. Систематизація та узагальнення теоретичних знань

Завдання 1.

Повтори блок № 5.
Дай письмово відповідь на питання , запропоновані вчителем.

Завдання 2.

Усно виконай вправи:

Кут якого виду зображено на рисунку?

А	Б	В	Г
Гострий	Тупий	Прямий	Розгорнутий

Який вид зображеного трикутника?

А	Б	В	Г
Рівносторонній	Рівнобедрений	Прямокутний	Різносторонній

Яка градусна міра кута KLM?

А	Б	В	Г

Обери правильний і найзручніший, на твій погляд, спосіб обчислення периметра рівнобедреного трикутника зі сторонами 8 см і основою 4 см.

А	Б	В	Г

ІІ. Систематизація та узагальнення практичних умінь та навичок

Завдання 3.

Письмово виконай вправи:

Які із даних кутів гострі, прямі, тупі і розгорнуті: , , , , , , ?
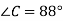
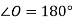
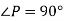
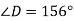
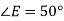
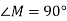
Виміряй кут АОВ транспортиром і побудуй його в зошиті.

Побудуй , градусна міра якого на більша

за градусну міру кута АОВ. Підпиши на малюнках

градусні міри кутів.

Одна сторона трикутника дорівнює 42 см, що на 24 см більше, ніж друга сторона. Третя сторона в 3 рази більша за другу. Знайди периметр трикутника.
Периметр рівнобедреного трикутника дорівнює 70 см, а його бічна сторона – 27 см. Знайди основу трикутника.
Периметр рівнобедреного трикутника дорівнює 60 см, а його основа 24 см. Знайди бічну сторону трикутника.
Яка градусна міра кута, утвореного стрілками годинника?

Тема №6. Прямокутник, квадрат, прямокутний паралелепіпед

Урок №1

Прямокутник, квадрат, прямокутний паралелепіпед

«Справжній скарб

для людини – вміння трудитися»

Езоп

Питання

Прямокутник, квадрат.
Площа прямокутника і квадрата.
Рівні фігури.
Прямокутний паралелепіпед, куб, піраміда.
Об’єм прямокутного паралелепіпеда, куба.

Література

Істер О.С. Математика: підручник для 5 класу. – §§ 22 – 26, ст. 165 – 201.

1. Прямокутник, квадрат
1.1	Прямокутник – чотирикутник, у якого всі кути прямі.
1.2	Формула для обчислення периметра прямокутника:
1.3	Прямокутник, у якого всі сторони рівні між собою, називається квадратом.
1.4	Формула для обчислення периметра квадрата:
2. Площа прямокутника і квадрата
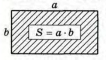
2.5	Для обчислення площі прямокутника, треба його довжину помножити на ширину.
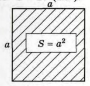
2.6	Формула для знаходження площі квадрата:
2.7	Площа фігури дорівнює сумі площ її частин.
3. Рівні фігури
3.8	Дві фігури, які можна накласти одна на одну так, щоб вони сумістилися, називаються рівними.
3.9	Відрізки, які мають однакові довжини, рівні.
3.10	Кути, що мають однакові градусні міри, рівні між собою.
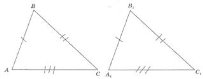
3.11	Трикутники, що мають рівні сторони і кути, рівні між собою.
3.12	Прямокутники, що мають рівні суміжні сторони, рівні між собою.
3.13	Властивості рівних фігур: рівні многокутники мають рівні периметри; рівні фігури мають рівні площі.
4.Прямокутний паралелепіпед, куб, піраміда
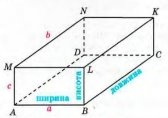
4.14	Уявлення про прямокутний паралелепіпед дають такі предмети: коробка сірників, цеглина, книга і т. д. S = 2(ab + bс + ас) – площа поверхні прямокутного паралелепіпеда
4.15	Прямокутники, з яких складається поверхня прямокутного паралелепіпеда, називаються його гранями, сторони граней – ребрами паралелепіпеда, вершини граней – вершинами паралелепіпеда.
4.16	Прямокутний паралелепіпед, у якого всі ребра рівні, називається кубом. S = 6a² – площа поверхні куба
4.17	Піраміда – фігура, поверхня якої складається з основи і бічних граней. Бічні грані піраміди – трикутники, основа – будь-який многокутник.
5. Об’єм прямокутного паралелепіпеда, куба
5.18	Об’єм прямокутного паралелепіпеда дорівнює добутку трьох його вимірів (довжини, ширини, висоти)
5.19	Формула для знаходження об’єму куба:

Запам’ятай!

Одиниці об’єму Одиниці площі

1 → 1 → 1 → 1 1 → 1 → 1 → 1

1000 1000 1000 100 100 100

Урок №2

«Просіть і буде вам

дано, шукайте і знайдете…»

Євангеліє від Матвія 7:7

Фронтальне опрацювання матеріалу

Прямокутник, квадрат

І. Робота над засвоєнням понять, термінів і правил

Завдання 1.

Повтори тези 1.1. – 1.4 блоку № 6.
Усно дай відповіді на питання:

Що називають прямокутником?
Як називають сусідні сторони прямокутника?
Які сторони прямокутника називають протилежними?
Яку властивість мають протилежні сторони прямокутника?
За якою формулою можна обчислити периметр прямокутника?
Який прямокутник називають квадратом?
За якою формулою можна обчислити периметр квадрата, сторона якого дорівнює а?
Що спільного в будь-якого прямокутника і квадрата? У чому їх відмінність?
Наведіть приклади предметів, які мають форму прямокутника, зокрема квадрата.

ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ

Завдання 2.

Виконай письмово вправи з підручника, стор. 166 – 167: 753, 756, 758, 760, 762 (1).

ІІІ. Відпрацювання умінь і навичок розв’язування нестандартних задач

Завдання 3.

Чи можна квадрат поділити на 31 квадратик?

Урок №3

«Математика – гімнастика для розуму»

О.В. Суворов

Фронтальне опрацювання матеріалу

Рівні фігури. Площа прямокутника і квадрата

І. Робота над засвоєнням понять, термінів і правил

Завдання 1.

Повтори тези 2.5 – 3.13 блоку № 6.
Усно дай відповідь на питання:

Які фігури називають рівними?
За якою формулою знаходять площу прямокутника; площу квадрата?
В яких одиницях виражають площі земельних ділянок?
Чи правильне твердження, що рівні фігури мають рівні площі?
Як знайти площу фігури, якщо вона поділена на частини?
Дайте визначення прямокутника і квадрата.

Завдання2.

Усно розв’яжи вправи:

У вільну комірку впишіть число:

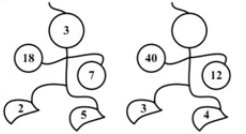
Безымянный.jpg

Яке слово зайве?

ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ

Завдання 3.

Виконай усно вправу 768, стор. 169.
Виконай письмово вправу 779, стор.171.
Виконай усно вправу 785, стор.175.
Виконай письмово вправу 790, стор. 176.
Використовуючи співвідношення між величинами, виконай письмово вправу 800, стор. 177.

ІІІ. Відпрацювання умінь і навичок розв’язування нестандартних задач

Завдання 4.

Знайди площу фігури, зображеної на рисунку:

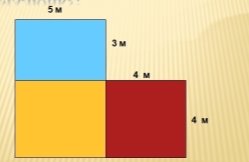
Вкажи, яку одиницю вимірювання (А – Е) зручно використати для вимірювання площі конкретної фігури (1 – 6).

1 А

2 Б

3 В

4 Г

5 Д

6 Е

Урок №4

«Як приємно дізнатися,

що ти чогось навчився»

Жан Батист Мольєр

Фронтальне опрацювання матеріалу

Прямокутний паралелепіпед, куб, піраміда

І. Робота над засвоєнням понять, термінів і правил

Завдання 1.

Повтори тези 4.14 – 4.17 блоку № 6.
Усно дай відповіді на питання:

Які предмети дають уявлення про прямокутний паралелепіпед?
Що є вершинами, ребрами і гранями прямокутного паралелепіпеда?
Скільки вершин, ребер та граней має прямокутний паралелепіпед?
Як називають виміри прямокутного паралелепіпеда?
Що називається кубом?
Що є гранями куба?
Чому дорівнює площа поверхні прямокутного паралелепіпеда, куба?
З чого складається поверхня піраміди?
Чим є бічні грані, а чим – основа піраміди?

Завдання 2.

Усно розв’яжи вправи, запропоновані вчителем (презентація).

ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ

Завдання 3.

Письмово розв’яжи вправи:

Знайди площу поверхні прямокутного паралелепіпеда, який має виміри . Для цього продовж запис: S = 2(ab + bс + ас)….
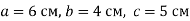
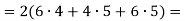Необхідно зробити відкритий дерев'яний ящик, що має форму прямокутного паралелепіпеда з вимірами 14 дм, 10дм, 7дм. Яка площа поверхні такого ящика? (Використай формулу площі поверхні прямокутного паралелепіпеда, теза 4.14 блоку № 6).
Необхідно поклеїти шпалерами кімнату, розміри якої 7 м на 4 м, висота кімнати 3 м. Вікна та двері кімнати займають площу 9 м². Скільки рулонів шпалер необхідно мати, якщо площа одного рулону становить 10 м²?

ІІІ. Відпрацювання умінь і навичок розв’язування нестандартних задач

Завдання 4.

Письмово розв’яжи вправи з підручника, стор. 188: 863; 866.

Урок №5

«Не будь переможений

злом, але перемагай зло добром»

Послання ап. Павла до римлян 12:21

Фронтальне опрацювання матеріалу

Об’єм прямокутного паралелепіпеда і куба

І. Робота над засвоєнням понять, термінів і правил

Завдання 1.

Повтори тези 4.14 – 5.19 блоку № 6.
Усно дай відповіді на питання:

Які предмети дають уявлення про прямокутний паралелепіпед?
Як називають виміри прямокутного паралелепіпеда?
Що називається кубом?
Чому дорівнює площа поверхні прямокутного паралелепіпеда, куба?
Чому дорівнює об’єм прямокутного паралелепіпеда?
Як записується формула об’єму куба?

Завдання 2.

Усно розв’яжи вправи, стор. 193 підручника: 873; 874.

ІІ. Відпрацювання умінь і навичок розв’язування задач і вправ

Завдання 3.

Розглянь приклад 1 на стор. 191 підручника.
Користуючись розглянутим прикладом, письмово розв’яжи вправи, стор. 193 підручника: 875; 877.

Завдання 4.

Прочитай правило на стор. 191 підручника про обчислення об’єму прямокутного паралелепіпеда через площу основи і висоту.
Користуючись цим правилом, виконай вправу 882, стор.194 підручника.

Завдання 5.

Розглянь вправу 884, стор.194 підручника.
Користуючись розглянутим ланцюжком, розв’яжи вправу 885, стор. 194 підручника.

ІІІ. Відпрацювання умінь і навичок розв’язування нестандартних задач

Завдання 6.

Письмово розв’яжи вправи з підручника, стор. 195 – 196: 888; 893; 904.

Завдання 7.

Розглянь вправу 909, стор. 197 підручника.
Користуючись розглянутим прикладом, письмово розв’яжи вправу:

У скільки разів збільшиться об’єм прямокутного паралелепіпеда, якщо його довжину збільшити в 3 рази, ширину — у 2 рази, а висоту — у 2 рази?

Готуємось до індивідуального опрацювання матеріалу

Одна сторона прямокутника 21 см, а друга – на 8 см більша від неї. Обчисли периметр та площу прямокутника.
Побудуй квадрат, периметр якого дорівнює 16 см. Знайди його площу.
Ширина прямокутного паралелепіпеда дорівнює 8 см, довжина – на 4 см більша, ніж ширина, а висота – у 3 рази менша, ніж довжина. Знайдіть об’єм даного паралелепіпеда.
Корт – спортивний майданчик, розмічений для гри в теніс, має площу 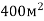. Довжина корту 10 м. Який його периметр?

Урок №7

Бо чим серце наповнене,

те говорять уста

Євангелія від Матвія 12:34

Внутрішньопредметне узагальнення матеріалу

Прямокутник, квадрат, прямокутний паралелепіпед

І. Систематизація та узагальнення теоретичних знань

Завдання 1.

Повтори блок № 6.
Дай письмово відповідь на питання , запропоновані вчителем.

Завдання 2.

Усно виконай вправи:

Знайди площу прямокутника, якщо одна з його сторін 9 см, а інша є меншою від неї на 3 см.

А	Б	В	Г

Знайди об’єм куба, ребро якого дорівнює 5 см.

А	Б	В	Г

Знайди об’єм прямокутного паралелепіпеда, якщо його виміри дорівнюють 4 дм, 6 дм, 1 дм.

А	Б	В	Г

ІІ. Систематизація та узагальнення практичних умінь та навичок

Завдання 3.

Письмово виконай вправи:

Довжина прямокутного паралелепіпеда дорівнює 24 см, а ширина у 6 разів менша від довжини, а висота на 16 см більша від ширини. Обчисли об’єм паралелепіпеда.
Поле прямокутної форми має площу 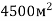, а його ширина 50 м. Обчисли периметр поля.
Сторони прямокутника дорівнюють 8 мм і 10 мм. Знайди площу квадрата, периметр якого дорівнює периметру даного прямокутника.
Об’єм води в басейні становить 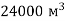. Довжина басейну 100 м, а ширина – 40 м. Знайди висоту басейну.
Сума довжин усіх ребер прямокутного паралелепіпеда 160 дм, а два його виміри 12 дм і 15 дм. Знайди третій вимір паралелепіпеда і його об’єм.

Повторення матеріалу, вивченого у І семестрі

Урок №1

«Золоті яблука на срібнім

тарелі – це слово, проказане часу свого»

Книга Приповістей Соломонових 25:11

Внутрішньопредметне узагальнення матеріалу

Узагальнення матеріалу, вивченого у І семестрі

І. Систематизація та узагальнення теоретичних знань

Завдання 1.

Повтори блоки № 1 – 6.
Усно дай відповідь на питання:

Що називають периметром многокутника?
Що називають трикутником?
Назви види трикутників за сторонами та за кутами.
Що називають прямокутником?
Що називають квадратом?
Як записуються формули для обчислення периметра прямокутника? Квадрата?
Як обчислити площу прямокутника? Квадрата?
Чому дорівнює об’єм прямокутного паралелепіпеда? Куба?
Які числа називаються натуральними?
Сформулюй властивості додавання натуральних чисел.
Сформулюй властивості віднімання натуральних чисел.
Сформулюй властивості множення натуральних чисел.
Що називають рівнянням?
Сформулюй правила розв’язування рівнянь.
Що називають координатним променем?

Завдання 2.

Усно розв’язати вправи:

Знайди об’єм куба, ребро якого дорівнює 7 см.

А	Б	В	Г

Знайди об’єм прямокутного паралелепіпеда, виміри якого дорівнюють 6 дм, 8 дм і 1 дм.

А	Б	В	Г

Обчисли: 20 963 + 19 237.

А	Б	В	Г
83 233	83 133	200	02

Обчисли у зручний спосіб: .

А	Б	В	Г
2360	23600	2630	26300

Обери правильний і найзручніший, на твій погляд, спосіб обчислення периметра рівнобедреного трикутника зі сторонами 8 см і основою 3 см.

А	Б	В	Г

ІІ. Систематизація та узагальнення практичних умінь та навичок

Письмово виконай вправи:

Завдання 3.

Об’єм води в басейні становить 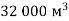. Довжина басейну 200 м, а ширина – 80 м. Знайди глибину басейну.

Сума довжин усіх ребер прямокутного паралелепіпеда 168 дм, а два його виміри – 12 дм і 14 дм. Знайти третій вимір паралелепіпеда і його об’єм.

Завдання 4.

Один художній альбом коштує 267 грн., а другий – на 38 грн. менше. Скільки коштують обидва альбоми разом?

Розв’яжи рівняння: 1) ; 2) .

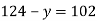
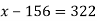
Знайди значення виразу , якщо .

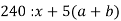
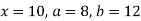
Накресли координатний промінь і познач на ньому точки A(0), B(3), C(7), D(8).

Знайди значення виразу: .

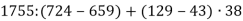Ящик, який має форму прямокутного паралелепіпеда з вимірами 32 см, 20 см і 12 см, заповнили кубиками з ребром 4 см. Скільки кубиків помістилося у ящик?

docx

Завантажити

Зберегти на потім

Додав(-ла)

Суворова Олеся Миколаївна

Пов’язані теми

Математика, 5 клас, Матеріали до уроків

Додано

26 червня 2018

Переглядів

5273

Оцінка розробки

Відгуки відсутні