НЕРОЗГАЛУЖЕНІ КОЛА ЗМІННОГО СТРУМУ Методичні вказівки для самостійної роботи при розв’язуванні задач для учнів електромонтажних професій

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

Департамент освіти і науки 

Закарпатської  обласної державної адміністрації

Тячівський професійний ліцей

 

 

 

 

НЕРОЗГАЛУЖЕНІ КОЛА ЗМІННОГО СТРУМУ

Методичні вказівки

для самостійної роботи

при розв’язуванні задач

для   учнів  електромонтажних професій

 

 

 

 

 

 

 

 

 

Викладач методист

М.В. Принц-Цимбаліста

 

 

 

 

 

 

 

 

 

 

 

 Методичні вказівки для самостійної роботи при розв’язуванні задач з електростатики розраховані на самостійне вивчення учнями матеріалу відповідно до робочої програми дисципліни «Електротехніка». В конспекті  на самостійне опрацювання виносяться питання по темі «НЕРОЗГАЛУЖЕНІ КОЛА ЗМІННОГО СТРУМУ».

У цьому розділі розглянемо електричні кола змінного струму, які мають три параметри R, L, С при послідовному з'єднаннях резисторів, котушок та конденсаторів.

Застосування векторних діаграм при розрахунку і дослідженні електричного кола змінного струму дозволяє наочно представляти аналізовані процеси і спрощувати електротехнічні розрахунки.

Самостійна робота є основним способом засвоєння учнями навчального матеріалу в час, вільний від обов'язкових навчальних занять.

Самостійна робота учнями може виконуватися як у бібліотеці,

комп'ютерному класі, так і в домашніх умовах.

Викладач визначає обсяг і зміст самостійної роботи, узгоджує її з іншими видами навчальної діяльності, проводить поточний та підсумковий контроль, аналізує результати самостійної навчальної роботи кожного учня.

Навчальний матеріал з електротехніки, передбачений робочим

навчальним планом для засвоєння учнями в процесі самостійної роботи,

виноситься на підсумковий контроль поряд з навчальним матеріалом, який опрацьовувався при проведенні навчальних занять.

Учні в процесі самостійного вивчення теоретичного матеріалу мають

засвоїти матеріал відповідних тем, використовуючи при цьому літературні джерела, названі в списку літератури.

Методичні вказівки  призначені для учнів професійно-технічних закладів освіти.

Розглянуто на засіданні методичної комісії

електромонтажних професій

     Протокол № 4  від 30.11. 2019.

 

 

НЕРОЗГАЛУЖЕНІ КОЛА ЗМІННОГО СТРУМУ

Загальні положення та основні визначення

Сила струму та густина струму  ,

де q – заряд , що проходить за час t через поперечний переріз S провідника,

е – елементарний заряд , n – концентрація  носіїв в провіднику, u_ср – середня швидкість носіїв заряду в провіднику.

Опір провідника

,

- питомий опір матеріалу провідника;

- довжина провідника.

Закон Ома:

для ділянки кола

;

для повного кола

,

електрорушійна сила джерела;

r – внутрішній  опір джерела.

 Послідовне з’єднання провідників

R = R₁ + R₂ +…+ R_n;

                                  I = I₁ = I₂ = … =  I_n;

U = U₁ + U₂ +…+U_n.

Паралельне з’єднання провідників

1/R = 1/R₁ + 1/R₂ +… + 1/R_n;

I = I₁ + I₂ +… + I_n;

U = U₁= U₂ =… =U_n.

 

Якщо  електричне коло з послідовно з’єднаним активним опором та індуктивністю  приєднали до джерела змінної синусоїдальної напруги, тоді у колі проходить струм, що відстає по фазі на кут φ від напруги. Кут зсуву фаз φ визначається за формулою .

Напруга  .

Повний опір кола з активним опором та індуктивністю:

.

Якщо  електричне коло з послідовно з’єднаним активним опором та ємністю  приєднали до джерела змінної синусоїдальної напруги, тоді у колі проходить струм, що випереджає по фазі на кут φ цю напругу. Кут зсуву фаз φ визначається за формулою .

Напруга  .

Повний опір кола з активним опором та ємністю:

.

Якщо  електричне коло з послідовно з’єднаним активним опором, індуктивним та ємнісним опорами  приєднали до джерела змінної синусоїдальної напруги, тоді у колі проходить змінний синусоїдальний струм.

 У цьому випадку напруга ; ; .

Повний опір кола з активним,  індуктивним та ємнісним опором:

.

 

Задача 12. Активний опір котушки R_К = 6Ом, індуктивний X_L = 10Ом. Послідовно до котушки приєднали активний опір R = 2Ом, і конденсатор опором X_С = 4Ом. До кола прикладена напруга U = 50В (діюче значення). Визначити: 1)повний опір кола Z ;   2)струм  I ;  3) коефіцієнт потужності sinφ;  4)активну  P, реактивну  Q , і повну  S потужності;  5) напругу U на кожному опорі. Накреслити  в масштабі векторну діаграму для електричного кола.

Рис. 42.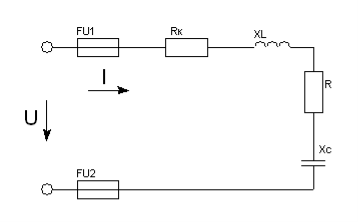

Р О З В’ Я З У В А Н Н Я.

1. Визначаємо повний опір кола:

2. Визначаємо струм :

I = U/ Z = 50/10 = 5А.

3. Визначаємо коефіцієнт потужності sinφ кола:

(за допомогою калькулятора обчислюємо значення оберненої тригонометричної функції  arcsin0,6 = 36˚52 ́. Тобто, φ = 36˚ 52 ́. Кут зсуву фаз φ знаходимо за функцією синус, щоб не втратити знак для кута, бо косинус є парною функцією, тому ця втрата є можливою).

4. Визначаємо активну потужність кола:

P = I²(R_K + R) = 5²·(6 + 2) = 200Вт .

Або     P = U I cosφ =50·5·0,8 =200Вт .

  Тут маємо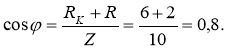       

5. Визначаємо реактивну потужність кола:

Q = I²(X_L  – X_C) = 5²·(10 – 4) = 150вар .

Або        Q = U Isinφ =50·5·0,6 = 150вар .

6. Визначаємо повну потужність кола :

Або    S = U I = 50·5 = 250В·А.

7. Визначаємо спад напруги на кожному опорі схеми:

U_{R k} = IR_K = 5·6 = 30В;     U_L = I X_L = 5·10 = 50В;

U_R = I R = 5·2 = 10В;     U_C = I X_C  = 5·4 = 20В.

8.Векторну діаграму починаємо будувати після того, коли вибрали масштаб для струму і напруги. Для струму:  в 1см – 1,0А   і для  напруги в 1см – 10В .

          

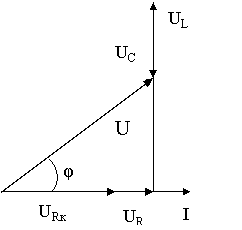
Рис. 43.

Вектор струму   відкладаємо горизонтально в масштабі  

Вздовж вектора струму відкладаємо вектори спаду напруги на активних опорах    і   :      і     

З кінця вектора   відкладаємо в бік випередження вектора струму на 90˚ вектор спаду напруги на індуктивному опорі довжиною  

З кінця вектора відкладаємо в бік відставання від вектора струму на 90˚ вектор спаду напруги  на конденсаторі довжиною Геометрична сума векторів ;  ; і    дорівнює вектору загальної напруги (рис.43), яка прикладена до електричного кола.

В І Д П О В І Д Ь.  Z = 10Ом;  I = 5А; sinφ = 0,6;  P = 200Вт ;  Q = 150вар;

                        S = 250В·А;  U_{R k} = 30В;  U_L = 50В;  U_R = 10В;  U_C = 20В.

 

 

Задача 13. Коло змінного струму (рис. 44) містить котушку з активним опором R_К , та індуктивним X_L . Послідовно до котушки приєднали активний опір R, і конденсатор з опором X_С . До кола прикладена напруга U (діюче значення); повний опір кола Z ; струм в колі  I ; коефіцієнт потужності sinφ; активна  потужність P, реактивна  Q , і повна  S. Накреслити  в масштабі векторну діаграму для електричного кола.

Рис. 44.

13.1. Дано: R_К = 6Ом ;  X_L = 3Ом ; R = 2Ом ; X_С = 9Ом ; U = 40В .   

 Знайти: Z ; I ; sinφ ; P ; Q ; S .

13.2. Дано: R_К = 4Ом ;  X_L = 4Ом ; R = 4Ом ; X_С = 10Ом ; I = 4А .   

 Знайти: Z ;  U ; sinφ ; P ; Q ; S .

13.3. Дано: R_К = 4Ом ;  X_L = 12Ом ; R = 2Ом ; X_С = 4Ом ; P = 24Вт .   

 Знайти: Z ;  U ; I ; sinφ ; Q ; S .

13.4. Дано: R_К = 3Ом ;  X_L = 2Ом ; R = 3Ом ; X_С = 10Ом ; Q_С = –160 вар .   

 Знайти: Z ;  U ; I ; sinφ ; P ; S .

13.5. Дано: R_К = 8Ом ;  X_L = 20Ом ; R = 4Ом ; X_С = 4Ом ; Q_L = 500 вар .   

 Знайти: Z ;  U ; I ; sinφ ; P ; S .

 

Задача 14. Для кола змінного струму (рис. 45) задано величину опору кожного елемента, а також один додатковий параметр. Визначити вказані електричні величини і накреслити  в масштабі векторну діаграму.

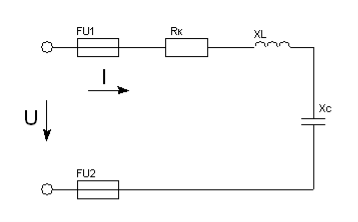
Рис. 45.

14.1. Дано: R_К = 4Ом ;  X_L = 6Ом ; X_С = 3Ом ; Q_L = 150 вар .   

 Знайти: Z ;  U ; I ; sinφ ; P ; S .

14.2. Дано: R_К = 3Ом ;  X_L = 2Ом ; X_С = 6Ом ; U = 50В .   

 Знайти: Z ;  I ; sinφ ; P ; Q ; S .

14.3. Дано: R_К = 6Ом ;  X_L = 10Ом ; X_С = 2Ом ; I = 5А .   

 Знайти: Z ;  U ; sinφ ; P ; Q ; S .

14.4. Дано: R_К = 8Ом ;  X_L = 4Ом ; X_С = 10Ом ; P = 800Вт .   

 Знайти: Z ;  I ; sinφ ; U ; Q ; S .

14.5. Дано: R_К = 12Ом ;  X_L = 18Ом ; X_С = 2Ом ; S = 500В·А .   

 Знайти: Z ;  I ; sinφ ; P ; Q ; U.

Задача 15. Для кола змінного струму (рис. 46) задано величину опору кожного елемента, а також один додатковий параметр. Визначити вказані електричні величини і накреслити  в масштабі векторну діаграму.

Рис. 46.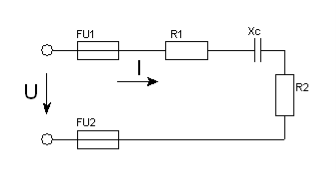

15.1. Дано: R₁ = 10Ом ; R₂  = 6Ом ; X_С = 12Ом ; I = 5А .   

 Знайти: Z ;  U ; sinφ ; P ; Q ; S

15.2. Дано: R₁ = 5Ом ; R₂  = 3Ом ; X_С = 6Ом ; S = 500В·А .   

 Знайти: Z ;  I ; sinφ ; P ; Q ; U.

15.3. Дано: R₁ = 2Ом ; R₂  = 2Ом ; X_С = 3Ом ; P = 100Вт .   

 Знайти: Z ;  I ; sinφ ; U ; Q ; S .

15.4. Дано: R₁ = 4Ом ; R₂ = 2Ом ; X_С = 8Ом ; U_R1 = 20В .   

 Знайти: Z ;  I ; sinφ ; P ; Q ; S .

15.5. Дано: R₁ = 2Ом ;  R₂ = 1Ом ; X_С = 4Ом ; Q_С = –100 вар .   

 Знайти: Z ;  U ; I ; sinφ ; P ; S .

Задача 16. Для кола змінного струму (рис. 47) задано величину опору кожного елемента, а також один додатковий параметр. Визначити вказані електричні величини і накреслити  в масштабі векторну діаграму.

Рис. 47.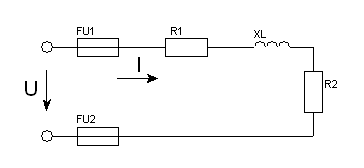

16.1. Дано: R₁ = 6Ом ; R₂  = 2Ом ; X_L = 6Ом ; P_R1 = 150Вт .   

 Знайти: Z ;  I ; sinφ ; U ; Q ; S .

16.2. Дано: R₁ = 8Ом ; R₂  = 4Ом ; X_L  =16Ом ; S = 320В·А .   

 Знайти: Z ;  I ; sinφ ; P ; Q ; U.

16.3. Дано: R₁ = 3Ом ;  R₂ = 1Ом ; X_L = 3Ом ; Q_L = 80 вар .   

 Знайти: Z ;  U ; I ; sinφ ; P ; S .

16.4. Дано: R₁ = 4Ом ; R₂  = 4Ом ; X_L = 6Ом ; I = 2А .   

 Знайти: Z ;  U ; sinφ ; P ; Q ; S

16.5. Дано: R₁ = 10Ом ; R₂ = 6Ом ; X_L = 12Ом ; U = 100В .   

 Знайти: Z ;  I ; sinφ ; P ; Q ; S .

Задача 17. Для кола змінного струму (рис. 48) задано величину опору кожного елемента, а також один додатковий параметр. Визначити вказані електричні величини і накреслити  в масштабі векторну діаграму.

Рис. 48.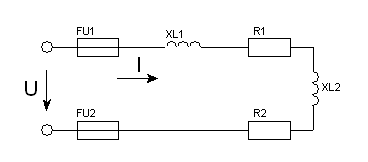

17.1. Дано: R₁ = 4Ом ; R₂  = 4Ом ; X_L1  = 3Ом ; X_L2  = 3Ом ; S = 360В·А .   

 Знайти: Z ;  I ; sinφ ; P ; Q ; U.

Р О З В’ Я З У В А Н Н Я.

1. Визначаємо повний опір кола:

2. Визначаємо напругу з таких двох формул:

                         

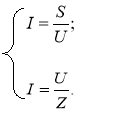
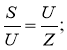
3. Визначаємо струм :

I = U/ Z = 60/10 = 6А.

4. Визначаємо коефіцієнт потужності sinφ кола:

(за допомогою калькулятора обчислюємо значення оберненої тригонометричної функції  arcsin0,6 = 36˚52 ́. Тобто, φ = 36˚ 52 ́. Кут зсуву фаз φ знаходимо за функцією синус, щоб не втратити знак для кута, бо косинус є парною функцією, тому ця втрата є можливою).

5. Визначаємо активну потужність кола:

P = I²(R₁ + R₂) = 6²·(4 + 4) = 288Вт .

Або     P = U I cosφ =60·6·0,8 =288Вт .

  Тут маємо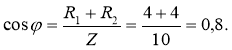       

6. Визначаємо реактивну потужність кола:

Q = I²(X_L1  + X_L2) = 6²·(3 + 3) = 216вар .

Або        Q = U Isinφ =60·6·0,6 = 216вар .

7. Визначаємо спад напруги на кожному опорі схеми:

U_L1 = I X_L1 = 6·3 = 18В;    U_{R 1} = IR₁ = 6·4 = 24В;

U_L2 = I X_L2  = 6·3 = 18В;     U_R2 = I R₂ = 6·4 = 24В .

 8.Векторну діаграму починаємо будувати після того, коли вибрали масштаб для струму і напруги. Для струму:  в 1см – 1,0А   і для  напруги в 1см – 10В .

          

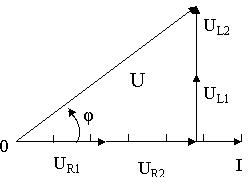
Рис. 48, a.

Вектор струму   відкладаємо горизонтально в масштабі  

Вздовж вектора струму відкладаємо вектори спаду напруги на активних опорах    і   :      і     

З кінця вектора   відкладаємо в бік випередження вектора струму   на 90˚ вектор спаду напруги на індуктивному опорі X_L1 довжиною  

З кінця вектора   відкладаємо в бік випередження від вектора струму   на 90˚ вектор спаду напруги на індуктивному опорі X_L2  довжиною Геометрична сума векторів ;  ; і    дорівнює вектору загальної напруги (рис.48, a), яка прикладена до електричного кола.

В І Д П О В І Д Ь.  Z = 10Ом;   I = 6А;   sinφ = 0,6;   P = 288Вт;

                                 Q = 216вар;  U = 60В.

 

17.2. Дано: R₁ = 6Ом ; R₂  = 10Ом ; X_L1 = 8Ом ; X_L2  = 4Ом ; P = 400Вт .   

 Знайти: Z ;  I ; sinφ ; U ; Q ; S .

17.3. Дано: R₁ = 4Ом ;  R₂ = 8Ом ; X_L1 = 10Ом ; X_L2  = 6Ом ;  Q  =  64вар .   

 Знайти: Z ;  U ; I ; sinφ ; P ; S .

17.4. Дано: R₁ = 2Ом ; R₂ = 4Ом ; X_L1 = 2Ом ; X_L2  = 6Ом ; U = 60В .   

 Знайти: Z ;  I ; sinφ ; P ; Q ; S .

17.5. Дано: R₁ = 6Ом ; R₂  = 2Ом ; X_L1 = 4Ом ; X_L2  = 2Ом ;  I = 4А .   

 Знайти: Z ;  U ; sinφ ; P ; Q ; S

Задача 18. Для кола змінного струму (рис. 49) задано величину опору кожного елемента, а також один додатковий параметр. Визначити вказані електричні величини і накреслити  в масштабі векторну діаграму.

Рис. 49.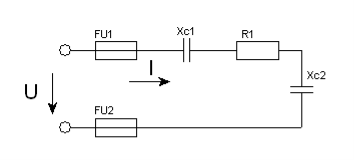

18.1. Дано: R₁ = 6Ом ; X_С1  = 5Ом ; X_С2  = 3Ом ; S = 160В·А .   

 Знайти: Z ;  I ; sinφ ; P ; Q ; U.

Р О З В’ Я З У В А Н Н Я.

1. Визначаємо повний опір кола:

2. Визначаємо напругу з таких двох формул:

                         

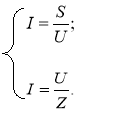
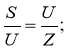
3. Визначаємо струм :

I = U/ Z = 40/10 = 4А.

4. Визначаємо коефіцієнт потужності sinφ кола:

(за допомогою калькулятора обчислюємо значення оберненої тригонометричної функції  arcsin(– 0,8) = – 53˚8 ́. Тобто, φ = – 53˚ 8 ́. Кут зсуву фаз φ знаходимо за функцією синус, щоб не втратити знак для кута, бо косинус є парною функцією, тому ця втрата є можливою).

5. Визначаємо активну потужність кола:

P = I²R₁ = 4²·6 = 96Вт .

Або     P = U I cosφ = 40·4· cos(– 53˚ 8΄)   = 40·4· 0,6 = 96Вт .

  Тут маємо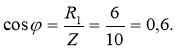       

6. Визначаємо реактивну потужність кола:

Q = I²(X_С1  + X_С2) = 4²·(–5 – 3) = – 128вар .

Або        Q = U Isinφ = 40·4·(– 0,8) = – 128вар .

7. Визначаємо спад напруги на кожному опорі схеми:

U_С1 = I X_С1 = 4·5 = 20В;    U_{R 1} = IR₁ = 4·6 = 24В;

U_С2 = I X_С2  = 4·3 = 12В .

  8.Векторну діаграму починаємо будувати після того, коли вибрали масштаб для струму і напруги. Для струму:  в 1см – 1,0А   і для  напруги в 1см – 4В .

          

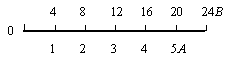
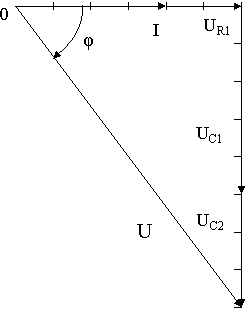
Рис. 49, a.

Вектор струму   відкладаємо горизонтально в масштабі  

Вздовж вектора струму відкладаємо вектори спаду напруги на активному опорі  :    

З кінця вектора   відкладаємо в бік відставання від вектора струму   на 90˚ вектор спаду напруги на ємнісному опорі X_С1 довжиною  

З кінця вектора   відкладаємо в бік відставання від вектора струму   на 90˚ вектор спаду напруги на ємнісному опорі X_С2  довжиною Геометрична сума векторів ;   і    дорівнює вектору загальної напруги (рис.49, a), яка прикладена до електричного кола.

В І Д П О В І Д Ь.  Z = 10Ом;   I = 4А;  sinφ = – 0,8;

                             P = 96Вт ;  Q = – 128вар;  U = 40В.

 

18.2. Дано: R₁ = 3Ом ;  X_С1 = 2Ом ; X_С2  = 2Ом ;  I = 4А .   

 Знайти: Z ;  U ; sinφ ; P ; Q ; S

18.3. Дано: R₁ = 8Ом ; X_С1 = 4Ом ; X_С2  = 2Ом ; U = 40В .   

 Знайти: Z ;  I ; sinφ ; P ; Q ; S .

18.4. Дано: R₁ = 16Ом ;  X_С1 = 4Ом ; X_С2  = 8Ом ;  Q  = – 300вар .   

 Знайти: Z ;  U ; I ; sinφ ; P ; S .

18.5. Дано: R₁ = 12Ом ; X_С1 = 10Ом ; X_С2  = 6Ом ; P = 48Вт .   

 Знайти: Z ;  I ; sinφ ; U ; Q ; S .

Задача 19. Для кола змінного струму (рис.50) задано величину опору кожного елемента, а також один додатковий параметр. Визначити вказані електричні величини і накреслити  в масштабі векторну діаграму.

Рис. 50.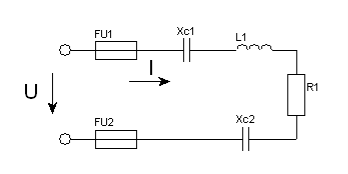

19.1. Дано: R₁ = 8Ом ; X_L1 = 12Ом ; X_С1 = 4Ом ; X_С2  = 2Ом ; P = 200Вт.   

 Знайти: Z ;  I ; sinφ ; U ; Q ; S .

19.2. Дано: R₁ = 12Ом ; X_L1 = 4Ом ;  X_С1 = 12Ом ; X_С2  = 8Ом ;  I = 4А.   

 Знайти: Z ;  U ; sinφ ; P ; Q ; S

19.3. Дано: R₁ = 6Ом ; X_L1 = 12Ом ; X_С1 = 2Ом ; X_С2  = 2Ом ; U_L1 = 60В .   

 Знайти: Z ;  I ; sinφ ; P ; Q ; S .

19.4. Дано: R₁ = 4Ом ; X_L1 = 10Ом ; X_С1 = 4Ом ; X_С2  = 3Ом ; U _С2 = 15В .   

 Знайти: Z ;  I ; sinφ ; P ; Q ; S .

19.5. Дано: R₁ = 3Ом ; X_L1 = 8Ом ;   X_С1 = 2Ом ; X_С2  = 10Ом ;  Q  = – 400вар .   

 Знайти: Z ;  U ; I ; sinφ ; P ; S .

Задача 20. Для кола змінного струму (рис.51) задано величину опору кожного елемента, а також один додатковий параметр. Визначити вказані електричні величини і накреслити  в масштабі векторну діаграму.

Рис. 51.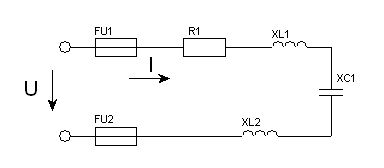

20.1. Дано: R₁ = 16Ом ; X_L1 = 10Ом ; X_L2  = 8Ом ; X_С1 = 6Ом ; U = 80В .   

 Знайти: Z ;  I ; sinφ ; P ; Q ; S .

20.2. Дано: R₁ = 6Ом ; X_L1 = 8Ом ; X_L2  = 4Ом ; X_С1 = 4Ом ; P = 54Вт.   

 Знайти: Z ;  I ; sinφ ; U ; Q ; S .

20.3. Дано: R₁ = 4Ом ; X_L1 = 8Ом ; X_L2  = 4Ом ;  X_С1 = 9Ом ; Q  = 75вар .   

 Знайти: Z ;  U ; I ; sinφ ; P ; S .

20.4. Дано: R₁ = 12Ом ; X_L1 = 14Ом ; X_L2  = 10Ом ; X_С1 = 8Ом ; U_R1 = 60В .   

 Знайти: Z ;  I ; sinφ ; P ; Q ; S .

20.5. Дано: R₁ = 6Ом ; X_L1 = 5Ом ; X_L2  = 3Ом ; X_С1 = 8Ом ; U_C1 = 16В .   

 Знайти: Z ;  I ; sinφ ; P ; Q ; S .

Задача 21. Для кола змінного струму (рис.52) задано величину опору кожного елемента, а також один додатковий параметр. Визначити вказані електричні величини і накреслити  в масштабі векторну діаграму.

Рис. 52.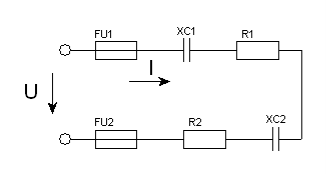

21.1. Дано: R₁ = 2Ом ; R₂ = 6Ом ;  X_С1 = 4Ом ; X_С2  = 2Ом ;   U_R2 = 24В .   

 Знайти: Z ;  I ; sinφ ; P ; Q ; S .

Р О З В’ Я З У В А Н Н Я.

1. Визначаємо струм за законом Ома для ділянки кола

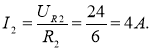
При послідовному  з’єднанні опорів в колі маємо І = І₂ = 4А.

2. Визначаємо повний опір кола:

3. Визначаємо напругу прикладену до кола

U = I · Z = 4·10 = 40В.

4. Визначаємо коефіцієнт потужності  sinφ  кола:

(за допомогою калькулятора обчислюємо значення оберненої тригонометричної функції  arcsin0,6 = 36˚52 ́. Тобто, φ = 36˚ 52 ́. Кут зсуву фаз φ знаходимо за функцією синус, щоб не втратити знак для кута, бо косинус є парною функцією, тому ця втрата є можливою).

5. Визначаємо активну потужність кола:

P = I²(R₁ + R₂) = 4²·(2 + 6) = 128Вт ,

або     P = U I cosφ =40·4·0,8 = 128Вт ,

тут маємо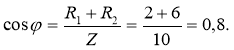       

6. Визначаємо реактивну потужність кола:

Q = I² (Х_С1+ X_С2) = 4² ·( – (4 + 2)) = 16 · (– 6) = – 96вар ,

або        Q = U Isinφ = 40·4·( – 0,6) = –  96вар .

7. Визначаємо повну потужність кола:

Або    S = U I = 40·4 = 160В·А.

8. Визначаємо спад напруги на опорах кола:

U_R1 = I R₁ = 4·2 = 8B;      U_R2 = I R₂ = 4·6 = 24B;

U_C1 = I X_C1 = 4·4 = 16B;    U_C2 = I X_C2 = 4·2 = 8B.

9. Побудову векторної діаграми починаємо з вибору масштабу для струму: в 1см – 1А;    і для напруги:   в 1см – 4В.

Вектор струму відкладаємо горизонтально довжиною 

Вздовж вектора струму відкладаємо вектори спаду напруги на активних опорах та довжиною  і 

З кінця вектора відкладаємо в бік відставання від вектора струму на 90˚ вектори спаду напруги на конденсаторах довжиною і

  довжиною . Геометрична сума векторів ;;; дорівнює вектору напруги  , яка прикладена до кола.

В І Д П О В І Д Ь. Z = 10Ом ; I = 4А ; sinφ = −0,6 ; P = 128Вт ; Q = – 96вар ; S = 160В·А .

21.2. Дано: R₁ = 10Ом ; R₂ = 6Ом ;  X_С1 = 8Ом ; X_С2  = 4Ом ;  I = 2А.   

 Знайти: Z ;  U ; sinφ ; P ; Q ; S

21.3. Дано: R₁ = 4Ом ; R₂ = 2Ом ;  X_С1 = 4Ом ; X_С2  = 4Ом ;  Q _С2  = – 256вар .   

 Знайти: Z ;  U ; I ; sinφ ; P ; S .

21.4. Дано: R₁ = 1Ом ; R₂ = 3Ом ;  X_С1 = 2Ом ; X_С2  = 1Ом ;  Q _С2  = – 48вар .   

 Знайти: Z ;  U ; I ; sinφ ; P ; S .

21.5. Дано: R₁ = 8Ом ; R₂ = 4Ом ; X_С1  = 6Ом ; X_С2  = 10Ом ; S = 180В·А .   

 Знайти: Z ;  I ; sinφ ; P ; Q ; U.

 

 

Задача 22. Для кола змінного струму (рис.53) задано величину опору кожного елемента, а також один додатковий параметр. Визначити вказані електричні величини і накреслити  в масштабі векторну діаграму.

Рис. 53.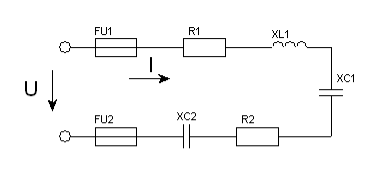

22.1. Дано: R₁ = 10Ом ; R₂ = 6Ом ; X_L1 = 18Ом ;  X_С1  = 4Ом ; X_С2  = 2Ом ;

 S = 80В·А .   

 Знайти: Z ;  I ; sinφ ; P ; Q ; U.

Р О З В’ Я З У В А Н Н Я.

1. Визначаємо повний опір кола:

2. Визначаємо струм з таких двох формул:

                         

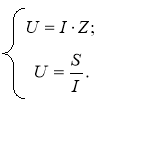
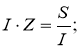
3. Визначаємо напругу:

U = I · Z = 2·20 = 40В.

4. Визначаємо коефіцієнт потужності  sinφ  кола:

(за допомогою калькулятора обчислюємо значення оберненої тригонометричної функції  arcsin0,6 = 36˚52 ́. Тобто, φ = 36˚ 52 ́. Кут зсуву фаз φ знаходимо за функцією синус, щоб не втратити знак для кута, бо косинус є парною функцією, тому ця втрата є можливою).

5. Визначаємо активну потужність кола:

P = I²(R₁ + R₂) = 2²·(10 + 6) = 64Вт ,

або     P = U I cosφ =40·2·0,8 = 64Вт ,

  тут маємо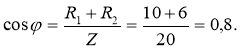       

6. Визначаємо реактивну потужність кола:

Q = I²(X_L1 – (Х_С1+ X_С2) = 2² ·(18 – (4 + 2)) = 48вар ,

або        Q = U Isinφ = 40·2·0,6 = 48вар .

7. Визначаємо спад напруги на кожному опорі схеми:

U_{R 1} = IR₁ = 2·10 = 20В;   U_L1 = I X_L1 = 2·18 = 36В;   U_С1 = I X_С1  = 2·4 = 8В;    

U_R2 = I R₂ = 2·6 = 12В;     U_С2 = I X_С2  = 2·2 = 4В .

8.Векторну діаграму починаємо будувати після того, коли вибрали масштаб для струму і напруги. Для струму:  в 1см – 0,2А   і для  напруги в 1см – 4В . Вектор струму   відкладаємо горизонтально в масштабі  

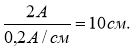
Вздовж вектора струму відкладаємо вектори спаду напруги на активних опорах    і   :      і     

З кінця вектора   відкладаємо в бік випередження вектора струму на 90˚ вектор спаду напруги на індуктивному опорі довжиною  

З кінця вектора відкладаємо в бік відставання від вектора струму на 90˚ вектори спаду напруги  на конденсаторах та довжиною Геометрична сума векторів ;  ; ; і     дорівнює вектору загальної напруги (рис.53, а), яка прикладена до електричного кола.

 

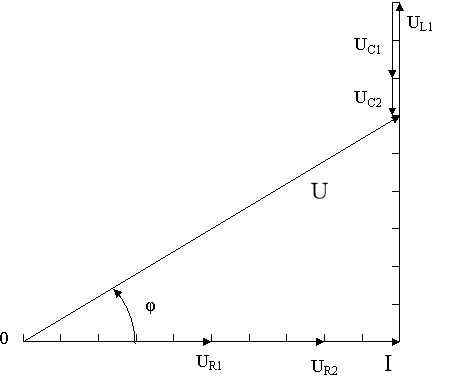           Рис. 53, а.

В І Д П О В І Д Ь.  Z = 20Ом;  I = 2А; sinφ = 0,6;

                                      P = 64Вт ;  Q = 48вар;  U = 40В.

 

22.2. Дано: R₁ = 2Ом ; R₂ = 2Ом ; X_L1 = 5Ом ;  X_С1 = 6Ом ; X_С2  = 2Ом ;

 Q   = – 192вар .   

 Знайти: Z ;  U ; I ; sinφ ; P ; S .

22.3. Дано: R₁ = 8Ом ; R₂ = 8Ом ; X_L1 = 12Ом ; X_С1 = 4Ом ; X_С2 = 2Ом ;

 P = 256Вт.   

 Знайти: Z ;  I ; sinφ ; U ; Q ; S .

22.4. Дано: R₁ = 4Ом ; R₂ = 2Ом ; X_L1 = 4Ом ;  X_С1 = 8Ом ; X_С2  = 4Ом ;

 Q _L1   = 16вар .   

 Знайти: Z ;  U ; I ; sinφ ; P ; S .

22.5. Дано: R₁ = 1Ом ; R₂ = 2Ом ; X_L1 = 6Ом ;   X_С1 = 8Ом ; X_С2  = 2Ом ; 

 U_С1 = 40В .   

 Знайти: Z ;  I ; sinφ ; P ; Q ; S .

Задача 23. На рис. 54 задана в масштабі векторна діаграма для нерозгалуженого електричного кола, струм в колі  I; спад напруги на кожному  опорі ( U₁ ,U₂ , U₃ і т. д.). Визначити характер і величину кожного опору. Накреслити еквівалентну схему кола. Обчислити  прикладену напругу і кут зсуву фаз φ.

Дано: I = 5А; U₁ = 20В ; U₂= 20В ; U₃ = 60 В; U₄ = 10 В (рис. 54).

Знайти:  R₁ ... R₄ ; U; φ.

 

Р О З В’ Я З У В А Н Н Я.

1. З векторної діаграми випливає, що напруга U₁ відстає від струму на кут 90˚, таким чином , на першій ділянці в коло ввімкнули конденсатор, опір якого

X_С1 = U₁/ I = 20/5 = 4Ом.

 

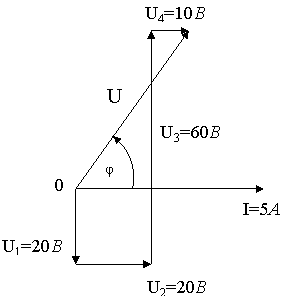Рис. 54.

 

2. Вектор напруги на другій ділянці напрямлений паралельно до вектора струму, тобто співпадає з ним по фазі. Значить, на другій ділянці ввімкнули активний опір

R₂ = U₂/I = 20/5 = 4Ом .

 

3. Вектор напруги на третій ділянці  випереджує  вектор струму на кут 90˚, що характерно для  індуктивності, опір якої

X_L3 = U₃/I = 60/5 = 12Ом .

4.На четвертій ділянці ввімкнено активний опір

R₄ = U₄/I = 10/5 = 2Ом .

5. Еквівалентна схема кола наведена на рис. 55.

6. З векторної діаграми визначаємо значення прикладеної напруги і кут зсуву фаз:

 

    φ = 53˚8΄.

Рис. 55.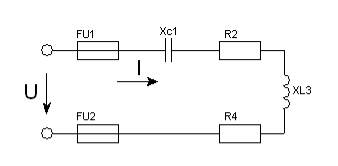

В І Д П О В І Д Ь.  X_С1 = 4Ом;  R₂ = 4Ом;  X_L3 = 12Ом;  R₄ = 2Ом;

                               φ = 53˚8΄;  U = 50В.

 

Задача 24. За даною векторною діаграмою для  електричного кола змінного струму з послідовним з’єднанням елементів (резисторів, індуктивностей, ємностей)  накреслити еквівалентну схему кола і визначити такі величини: 1) величину опору кожного елемента і повний опір кола Z; 2) напругу U прикладену  до електричного кола; 3) кут зсуву фаз φ (за величиною і напрямом); 4) активну  P, реактивну  Q  і повну  S потужність кола.  

 Рис. 56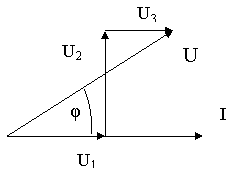 

24.1. Дано: I = 10А; U₁ = 10В ; U₂= 40В ; U₃ = 20 В (рис. 56).

 Знайти: Z; U; φ; P; Q; S.

Р О З В’ Я З У В А Н Н Я.

1. З векторної діаграми випливає, що вектор напруги  та  напрямлені паралельно до вектора струму, тобто співпадають з ним по фазі. Значить, на першій  і третій ділянці ввімкнули активні опори

R₁ = U₁/I = 10/10 = 1Ом .

R₃ = U₃/I = 20/10 = 2Ом .

2. Вектор напруги на другій ділянці випереджує  вектор струму на кут 90˚, що характерно для  індуктивності, опір якої

X_L2 = U₂/I = 40/10 = 4Ом .

3. Еквівалентна схема кола наведена на рис. 56, б.

Рис.56, б.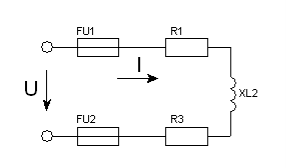

4. З векторної діаграми визначаємо значення прикладеної напруги і кут зсуву фаз:

 

    φ = 53˚8΄.

5. Визначаємо повний опір кола:

6. Визначаємо активну потужність кола:

P = I²(R₁ + R₃) = 10²·(1 + 2) = 300Вт ,

або     P = U I cosφ = 50·10·0,6 = 300Вт ,

  тут маємо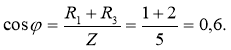       

7. Визначаємо реактивну потужність кола:

Q = I²X_L2  = 10²·4  = 400вар ,

або        Q = U Isinφ = 50·10·0,8 = 400вар .

8. Визначаємо повну потужність кола :

Або    S = U I = 50·10 = 500В·А.

В І Д П О В І Д Ь.  Z = 5Ом ;  U = 50В;    φ = 53˚8΄;

                                P = 300Вт ;  Q = 400вар ;  S = 500В·А.

 

24.2. Дано: I = 5А; U₁ = 15В ; U₂= 15В ; U₃ = 5 В (рис. 56).

Знайти: Z; U; φ; P; Q; S.

24.3. Дано: I = 2А; U₁ = 10В ; U₂= 12В ; U₃ = 6 В (рис. 56).

Знайти: Z; U; φ; P; Q; S.

24.4. Дано: I = 3А; U₁ = 36В ; U₂= 36В ; U₃ = 12 В (рис. 56).

 Знайти: Z; U; φ; P; Q; S.

24.5. Дано: I = 4А; U₁ = 24В ; U₂= 24В ; U₃ = 8 В (рис. 56).

 Знайти: Z; U; φ; P; Q; S.

 

Рис. 57.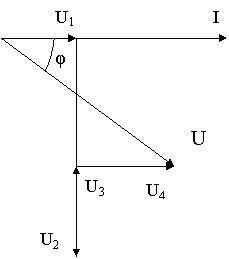

 

24.6. Дано: I = 4А; U₁ = 32В ; U₂= 80В ; U₃ = 16В; U₄ = 16В (рис. 57).

 Знайти: Z; U; φ; P; Q; S.

24.7. Дано: I = 10А; U₁ = 30В ; U₂= 50В ; U₃ = 20В; U₄ = 10В (рис. 57).

 Знайти: Z; U; φ; P; Q; S.

24.8. Дано: I = 5А; U₁ = 20В ; U₂= 30В ; U₃ = 20В; U₄ = 10В (рис. 57).

 Знайти: Z; U; φ; P; Q; S.

24.9. Дано: I = 2А; U₁ = 16В ; U₂= 40В ; U₃ = 8В; U₄ = 8В (рис. 57).

 Знайти: Z; U; φ; P; Q; S.

24.10. Дано: I = 1А; U₁ = 10В ; U₂= 20В ; U₃ = 8В; U₄ = 6В (рис. 57).

 Знайти: Z; U; φ; P; Q; S.

Рис.58.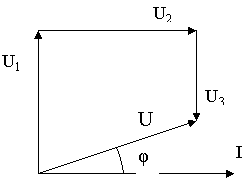

 

24.11. Дано: I = 3А; U₁ = 60В ; U₂= 48В ; U₃ = 24В (рис. 58).

Знайти: Z; U; φ; P; Q; S.

24.12. Дано: I = 4А; U₁ = 40В ; U₂= 12В ; U₃ = 24В (рис. 58).

Знайти: Z; U; φ; P; Q; S.

24.13. Дано: I = 2А; U₁ = 20В ; U₂= 16В ; U₃ = 8В (рис. 58).

Знайти: Z; U; φ; P; Q; S.

24.14. Дано: I = 5А; U₁ = 50В ; U₂= 30В ; U₃ = 10В (рис. 58).

Знайти: Z; U; φ; P; Q; S.

24.15. Дано: I = 3А; U₁ = 30В ; U₂= 24В ; U₃ = 12В (рис. 58).

Знайти: Z; U; φ; P; Q; S.

 

Рис. 59.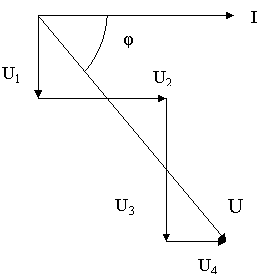

24.16. Дано: I = 2А; U₁ = 4В ; U₂= 8В ; U₃ = 12В; U₄ = 4В (рис. 59).

 Знайти: Z; U; φ; P; Q; S.

24.17. Дано: I = 5А; U₁ = 50В ; U₂= 40В ; U₃ = 30В; U₄ = 20В (рис. 59).

 Знайти: Z; U; φ; P; Q; S.

24.18. Дано: I = 4А; U₁ = 4В ; U₂= 8В ; U₃ = 12В; U₄ = 4В (рис. 59).

 Знайти: Z; U; φ; P; Q; S.

24.19. Дано: I = 10А; U₁ = 60В ; U₂= 20В ; U₃ = 20В; U₄ = 40В (рис. 59).

 Знайти: Z; U; φ; P; Q; S.

24.20. Дано: I = 8А; U₁ = 24В ; U₂= 8В ; U₃ = 8В; U₄ = 16В (рис. 59).

 Знайти: Z; U; φ; P; Q; S.

 

 

 

 

 

 

 Рис. 60.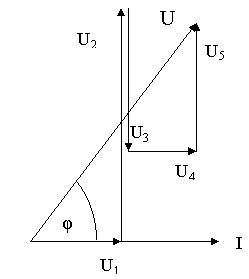 

24.21. Дано: I = 4А; U₁ = 12В; U₂= 20В; U₃ = 16В; U₄ = 4В; U₅ = 8В (рис. 60).

 Знайти: Z; U; φ; P; Q; S.

24.22. Дано: I = 2А; U₁ = 12В; U₂= 20В; U₃ = 12В; U₄ = 4В; U₅ = 4В (рис. 60).

 Знайти: Z; U; φ; P; Q; S.

24.23. Дано: I =3А; U₁ = 36В; U₂= 36В; U₃ =24В; U₄ = 18В; U₅ =24В (рис. 60).

 Знайти: Z; U; φ; P; Q; S.

24.24. Дано: I =5А; U₁ =10В; U₂= 50В; U₃ =40В; U₄ = 20В; U₅ = 30В (рис. 60).

 Знайти: Z; U; φ; P; Q; S.

24.25. Дано: I = 6А; U₁ = 48В; U₂= 84В; U₃ =24В; U₄ =24В; U₅ =36В (рис. 60).

 Знайти: Z; U; φ; P; Q; S.

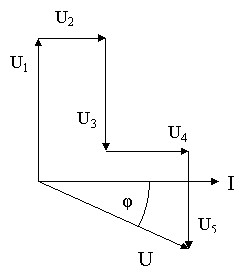Рис. 61.

24.26. Дано: I = 2А; U₁ = 16В; U₂ = 2В; U₃ = 12В; U₄ = 4В; U₅ = 10В (рис. 61).

 Знайти: Z; U; φ; P; Q; S.

24.27. Дано: I = 3А; U₁ = 18В; U₂ = 6В; U₃ = 12В; U₄ =12В; U₅ =30В (рис. 61).

 Знайти: Z; U; φ; P; Q; S.

24.28. Дано: I = 4А; U₁ = 16В; U₂ =24В; U₃ =20В; U₄ =40В; U₅ =44В (рис. 61).

 Знайти: Z; U; φ; P; Q; S.

24.29. Дано: I = 6А; U₁ = 30В; U₂ = 6В; U₃ = 18В; U₄ =12В; U₅ =36В (рис. 61).

 Знайти: Z; U; φ; P; Q; S.

24.30. Дано: I = 5А; U₁ = 20В; U₂ =20В; U₃ =10В; U₄ =20В; U₅ =40В (рис. 61).

 Знайти: Z; U; φ; P; Q; S.

 

 Рис. 62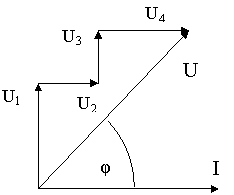 

 

24.31. Дано: I = 3А; U₁ = 9В ; U₂= 3В ; U₃ = 3В; U₄ = 6В (рис. 62).

 Знайти: Z; U; φ; P; Q; S.

24.32. Дано: I = 4А; U₁ = 20В ; U₂= 16В ; U₃ = 12В; U₄ = 8В (рис. 62).

 Знайти: Z; U; φ; P; Q; S.

24.33. Дано: I = 5А; U₁ = 50В ; U₂= 40В ; U₃ = 30В; U₄ = 20В (рис. 62).

 Знайти: Z; U; φ; P; Q; S.

24.34. Дано: I = 2А; U₁ = 8В ; U₂= 20В ; U₃ = 16В; U₄ = 12В (рис. 62).

 Знайти: Z; U; φ; P; Q; S.

24.35. Дано: I = 6А; U₁ = 12В ; U₂= 36В ; U₃ = 24В; U₄ = 12В (рис. 62).

 Знайти: Z; U; φ; P; Q; S.

 

 

 

  

 

 

 Рис. 63.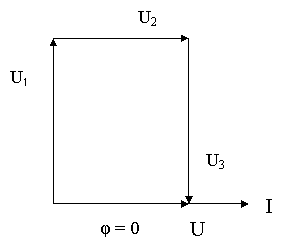 

24.36. Дано: I = 6А; U₁ = 18В ; U₂= 12В ; U₃ = 18 В (рис. 63).

Знайти: Z; U; P; Q; S.

Р О З В’ Я З У В А Н Н Я.

1. З векторної діаграми випливає, що напруга U₁ випереджує  струм на кут 90˚, таким чином, на першій ділянці в коло ввімкнули котушку, індуктивний опір якої

X_L1 = U₁/ I = 18B/6A = 3Ом.

2. Вектор напруги на другій ділянці напрямлений паралельно до вектора струму, тобто співпадає з ним по фазі. Значить, на другій ділянці ввімкнули активний опір

R₂ = U₂/I = 12B/6A = 2Ом .

 

3. Вектор напруги на третій ділянці  відстає від  вектора струму на кут 90˚, що характерно для  конденсатора, опір якої

X_С3 = U₃/I = 18В/6А = 3Ом .

4. Еквівалентна схема кола наведена на рис. 63, а.

5. З векторної діаграми визначаємо значення прикладеної напруги:

U = U₂ = 12В.

6. Визначаємо повний опір кола:

Рис. 63, а.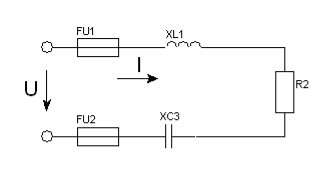

7. Визначаємо активну потужність кола:

P = I²R = 6²·2 = 72Вт,   або  P =UIcosφ = 12·6·1 = 72 Вт,  тут

 cosφ = cos0˚ = 1.

8. Реактивна потужність кола:

Q = I²( X_L1 – X_C3) = 6²·( 3 – 3 ) = 0, або

Q = UIsinφ = 12·6·0 = 0.

9. Повна потужність кола:

S = P = 72Вт, бо  Q = 0, або    S = UI = 12·6 = 72В·А.

В І Д П О В І Д Ь. Z = 2Ом; U = 12В; P = 72Вт; Q = 0; S = 72В·А.

 

 

24.37. Дано: I = 5А; U₁ = 50В ; U₂= 25В ; U₃ = 50 В (рис. 63).

Знайти: Z; U; P; Q; S.

24.38. Дано: I = 7А; U₁ = 56В ; U₂= 70В ; U₃ = 56 В (рис. 63).

Знайти: Z; U; P; Q; S.

24.39. Дано: I = 4А; U₁ = 60В ; U₂= 40В ; U₃ = 60 В (рис. 63).

Знайти: Z; U; P; Q; S.

24.40. Дано: I = 2А; U₁ = 36В ; U₂= 30В ; U₃ = 36 В (рис. 63).

Знайти: Z; U; P; Q; S.

 Рис. 64.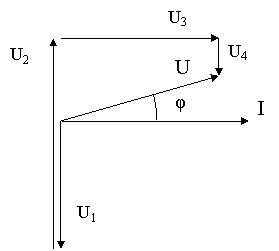 

24.41. Дано: I = 4А; U₁ = 32В ; U₂= 56В ; U₃ = 12В; U₄ = 8В (рис. 64).

 Знайти: Z; U; φ; P; Q; S.

24.42. Дано: I = 5А; U₁ = 20В ; U₂= 80В ; U₃ = 30В; U₄ = 20В (рис. 64).

 Знайти: Z; U; φ; P; Q; S.

24.43. Дано: I = 2А; U₁ = 4В ; U₂= 40В ; U₃ = 32В; U₄ = 12В (рис. 64).

 Знайти: Z; U; φ; P; Q; S.

24.44. Дано: I = 3А; U₁ = 6В ; U₂= 36В ; U₃ = 24В; U₄ = 12В (рис. 64).

 Знайти: Z; U; φ; P; Q; S.

24.45. Дано: I = 5А; U₁ = 20В ; U₂= 50В ; U₃ = 20В; U₄ = 15В (рис. 64).

 Знайти: Z; U; φ; P; Q; S.

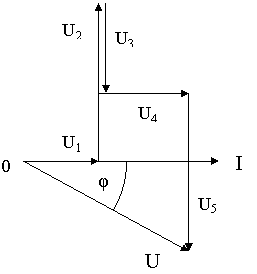Рис. 65.

24.46. Дано: I =10А; U₁ =20В; U₂ =40В; U₃ =30В; U₄ =20В; U₅ =40В (рис. 65).

 Знайти: Z; U; φ; P; Q; S.

24.47. Дано: I =8А; U₁ =48В; U₂ =64В; U₃ =32В; U₄ =16В; U₅ =80В (рис. 65).

 Знайти: Z; U; φ; P; Q; S.

24.48. Дано: I =6А; U₁ =12В; U₂ =30В; U₃ =24В; U₄ =6В; U₅ =30В (рис. 65).

 Знайти: Z; U; φ; P; Q; S.

24.49. Дано: I =5А; U₁ =30В; U₂ =40В; U₃ =30В; U₄ =50В; U₅ =70В (рис. 65).

 Знайти: Z; U; φ; P; Q; S.

24.50. Дано: I = 10А; U₁ = 50В; U₂ = 100В; U₃ = 60В; U₄ = 30В; U₅ =100В (рис. 65).

 Знайти: Z; U; φ; P; Q; S.

 

 

 

 

 

 

Л І Т Е Р А Т У Р А.

1. Гуржій А.М.,  Сільвестров А.М., Поворознюк Н.І. Електротехніка з основами промислової електроніки. – К.: Форум, 2002. – 382 с.: іл.

2. Китаев В. Е., Шляпинтох Л. С. Электротехника с основами промышленной электроники. М., «Высшая школа», 1973.  

3. Попов Ю. П.,  Шовкошитний І.І. Основи електротехніки, радіо- та мікроелектроніки. – Львів: Оріяна-Нова, 2001. – 167 с.