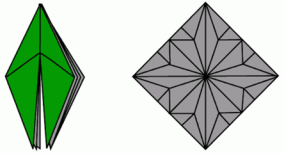
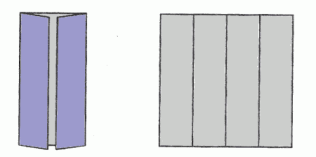
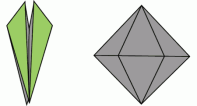
Орігамі та математика - одне ціле

Зміст:
Вступ........................................................................................................ 3

 Розділ 1: Елементи техніки орігамі... ...... .......................................... 4
1.1. Філософія складання орігамі......................................................... 4
1.2. Легенди орігамі. ............................................................................. 4 
1.3. "Радість знайомства з орігамі - тричі в житті".... ....................... 6
1.4. Азбука орігамі та базові форми.................................................... 7

1.5 Види і техніки орігамі……………………………………………10
 Розділ 2: Практична орігаметрія……………………………………12
2.1. А що таке орігаметрія?....... . ....................................................... 12

2.2 Знайомство з геометричними поняттями……………………….12
2.3.Орігаметричні задачі .................................................................... 13
2.4. Модульні орігамі ......................................................................... 15

2.5. Технологічний етап та математичні розрахунки………………16
2.6. Головоломки і орігамі ................................................................. 19

2.7.Орігамі в математиці…………………………………………….20

2.8. Орігамі в нашому житті…………………………………………23

Висновок  ............................................................................................ 26
Список літератури................................................................................27
 

 

 

 

 

 

 

 

 

 

 

Вступ.

Епіграфом до своєї роботи я вибрав японську народну мудрість :

Вдивляйтесь у звичайне – і побачите несподіване,

Вдивляйтесь у негарне – і побачите красиве,

Вдивляйтесь у просте – побачите складне.

Вдивляйтесь у частинки – і побачите ціле.

      Гіпотеза:
Мистецтво орігамі тісно пов'язано з математикою.
    Мета дослідження  :
-Вивчення орігамі, його походження і суті;
-Довести нерозривний зв'язок цього мистецтва з математикою.

    Завдання дослідження  :
-Вивчити історію походження орігамі.
-Проаналізувати зв'язок орігамі і математики.
-Показати практичне застосування математичних законів в орігамі.

    Методи дослідження :
-Пошук інформації з різних джерел(спеціальналітература, інтернет ресурси);
- Практична робота.

     Актуальність теми :

Наступного року мені належить вивчати такий предмет, як геометрія. Як мені здається - складною проблемою в розумінні геометрії залишається проблема просторового уявлення, яке пов'язане з практичною діяльністю і застосуванням принципу наочності. Ми вчимося на справах! Тому, якщо чому-небудь вчитися, необхідно робити все самому, інакше нічого не запам’ятаєш, оскільки в голові утримуються тільки ті знання, які застосовуються в практичній діяльності. А мистецтво орігамі якнайкраще підходить для різних вікових категорій. Можливо, саме тому майстри орігамі говорять, що при складанні фігурок "голова працює руками".

                            Розділ 1: Елементи техніки орігамі.
                                    1.1. Філософія складання.
Орігамі в його класичному варіанті - тільки квадрат, ніяких надрізів, народилося в Стародавній Японії. Незважаючи на те, що сам папір був винайдений у Китаї, саме в Японії здогадалися складати з неї дивовижні фігурки.
На Сході квадрат є не просто геометричною фігурою, а важливим символом. Неосяжність Всесвіту, в основі якої лежить квадрат, блискуче підкреслена в афоризмі Лао-Цзи: «У великого квадрата немає кутів».
У далекій давнині орігамі мало релігійне призначення, було храмовим мистецтвом. Виготовлення барвистих фігурок було священним ритуальним дією. Японці бачили містичну зв'язок між релігійними ритуалами та виробами з складеної папери. Адже "орі" означає "складений", а "камі" - "папір" і "бог" одночасно.
Втративши згодом своє ритуальне призначення, орігамі вийшло за межі храмів і досягло імператорського палацу. Уміння складати з паперу вважалося у придворних одним з ознак доброго освіти і вишуканих манер. В ті часи папір матеріалом було рідкісним і дорогим. Фігурки орігамі служили гербом і печаткою у деяких знатних родинах.
Пізніше мистецтвом складання з паперу стали займатися, в основному, жінки і діти. Воно стало частиною традицій і звичаїв, прикрасою японського побуту, карнавальних ходів, народних свят.
У другій половині XIX століття орігамі перейшло межі Японії. У країнах Європи почали знайомитися з класичними фігурками, виконаними в техніці орігамі.

   Бурхливий розвиток орігамі почалося тільки після другої світової війни, головним чином, завдяки зусиллям всесвітньо відомого майстра-орігаміста Акіри Йошізави. Саме він винайшов єдину універсальну систему знаків, за допомогою яких можна записати схему складання будь-фігурки.

1.2. Легенди орігамі.
Саме для того, щоб розбудити цікавість і потяг у нових учнів, майстри орігамі вигадували різні

історії — легенди про важливість орігамі в житті людини та історії в цілому. Найголовніша і відома легенда про це японському мистецтві безпосередньо пов'язана з самою значущою і важливою фігуркою орігамі — паперових журавликів. У країнах Сходу журавель вважається символом любові, віри і  надії. Люди здавна вірять, що якщо зробити тисячу таких фігурок, а потім подарувати їх все близьким і знайомим, то виповниться найзаповітніше бажання. 

      Сама легенда звучить приблизно так:« Колись давно на землі жив дуже бідний майстер, який все своє життя присвятив орігамі і був напрочуд добрий до всіх і до всього, що його оточувало. Він цілими днями складав з аркушів паперу різні фігурки, а потім роздавав дітям. Але одного разу він зустрів на дорозі мандрівного ченця і подарував йому фігурку журавлика. Чернець був зворушений. Потім він сказав: «Складай свої фігурки далі. Головне — твоя віра в їх важливість. Навіть якщо навколо війна, залишайся вірним своєму мистецтву, і воно віддячить тобі, зробивши тебе багатим і відомим». Незабаром і правда як за пророцтвом ченця почалася війна. Молоді пішли битися, але кінця цього жаху й видно не було. Тільки бідний майстер вперто продовжував переводити папір на свої фігурки. Розлютившись, люди вирішили спалити його майстерню. Але коли вони опинилися в ній, вони були вражені різноманітністю і пишністю фігурок. Тоді майстер подарував кожному фігурку за душі і за смаком. На очах у гостей майстер згорнув з листа журавлика, який тут же заплескав крилами і полетів — він був вісником світу. Люди повірили в себе, надихнулися, і незабаром перемога була за ними».

      Після другої світової війни журавлик став справжнім символом миру і свободи. А також символом порятунку від ядерної загрози та променевої хвороби. Це пов'язано з певною легендою, яка дуже схожа на правду і оповідає про дівчинку по імені Садако Сасакі. Вона народилася в 1943 році, а в 1945 р. під час бомбардування  Хіросіми  загинули її батьки. Хтось сказав їй, що якщо вона зробить тисячу журавликів, вона видужає. Садако скоро зрозуміла, що їй вже не стане краще, вона помре. І тоді вона почала дарувати своїх журавликів іншим хворим - кожен журавлик, якого згортала маленька Садако, був молитвою: молитвою про спасіння людини і молитвою про мир.

     Складаючи орігамі, люди часто задаються питанням: «А чому квадрат? І чому не можна різати? »

      На сході до квадрату завжди ставилися з особливою повагою. У Стародавньому Китаї він символізував землю. Вважалося, що земля має форму квадрата, над якою нависає купол неба. Форму квадрата мають і всі, що народилися на сході ігри: шахи, танграм. Квадрат - це найменший розмір кімнати в японському будинку - два татамі. Всі ієрогліфи можна вписати в квадрат. Досліджуючи можливості орігамі, сучасні майстри довели, що жодна форма не має такі можливості для складання, як квадрат.

      Що ж стосується заборони розрізати, то він прямо пов'язаний з переконанням, що все у Всесвіті пов'язане з усім. Всі форми перетікають одна в іншу. Як в фігурці орігамі, квадрат, видозмінюючись, дає життя новій формі. Розріз порушує єдине ціле.

1.3. «Радість знайомства з орігамі – тричі в житті».

Професор Кава Сіма Рюта займається вивченням фізіології мозку в Інституті вікової медицини при Університеті Тохоку. Він показав, що виконання орігамі збільшує потік крові, що проходить через префронтальну зону головного мозку, допомагаючи йому краще працювати. Ось чому у багатьох клубах для літніх людей відкрили гуртки орігамі. В одному з таких клубів, який називається «Сінія нэттоваку Сендай», раз на тиждень проводяться посиденьки за орігамі. Їх відвідують літні люди у віці від шістдесяти до вісімдесяти років. Своїм гаслом вони обрали слова: «Радість знайомства з орігамі – тричі в житті». Це означає, що перший раз люди зустрічаються з орігамі в дитинстві; потім, ставши батьками, вони розповідають про нього своїм дітям і, нарешті, в третій

вони відкривають орігамі вже в літньому віці.
Зараз в орігамі існує три основних течії:

     • Перша течія – традиційне орігамі, де в якості основи використовується

                                    квадрат.
      • Друга течія – моделі складаються з листів трикутної, прямокутної,  

п'яти-, шести-, восьмикутної форми.
      • Третя течія – модульне орігамі, моделі виготовляються з певного, іноді досить великого числа однотипних модулів.
Тобто всі фігури орігамі виконуються з геометричних фігур, значить це одна з точок дотику орігамі з математикою.

1.4. Азбука орігамі та базові форми.

Японська мудрість здавна говорить:
"Великий квадрат не має меж".
Спробуй просту скласти фігурку,
І вмить захопить цікава справа.

Навчання мистецтву орігамі починається з абетки орігамі та базових форм:

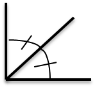
Перший крок  - ознайомиться зі знаками і позначеннями, що зустрічаються в схемах (Рис.1):

Наприклад:

Прямий кут          

 

 

 

 

Рівні частини або сторони Рис.1

Рівні кути

Азбука орігамі це рішення геометричних завдань, значить це ще одна з точок дотику орігамі з математикою.

Другий крок, ще трішечки наближає нас до цього дивовижного мистецтва. Тепер нам потрібно засвоїти базові схеми орігамі:

• Базова форма — вихідна форма, яка використовується при виготовленні фігури. З базових форм можна зробити безліч фігур як плоских, так і об'ємних.

 • Згини, виконані при створенні цих форм, ділять кути і грані навпіл.

Наприклад:    

Ромб: (Рис.2) Конверт:  Рис.4           Птаха: Рис.6 Подвійний квадрат: Рис.8 Катамаран: Рис.10

Трикутник: Рис.3         Повітряний змій:   Рис.5   Жабеня: Рис.7           Двері: Рис.9 Риба: Рис.11

Складаючи базові форми орігамі (Рис.2 – 11), я абсолютно непомітно для себе повторив деякі геометричні поняття: квадрат, прямокутник, трикутник, ромб. Тобто деякі базові форми - це геометричні фігури, отже це ще одна з точок дотику орігамі з математикою.

Складання фігур орігамі допомагає засвоїти такі поняття, як:

• Паралельні прямі.

 • Бісектриса. (Рис.12)

• Діагональ. (Рис.13)

 

 

 

 

 

 

 

   

                                                                                                    Рис.13

                          Рис.12                                                

Отже це ще одна з точок дотику орігамі з математикою.

1.5 Види і техніки орігамі

Модульне орігамі

Одним з популярних різновидів орігамі є модульне орігамі, в якому ціла фігура збирається з багатьох однакових частин (модулів). Кожен модуль складається за правилами класичного орігамі з одного аркуша паперу, а потім модулі з'єднуються шляхом вкладання їх один в одного, що не дає конструкції розпастися.

Просте орігамі

Просте орігамі - стиль орігамі, придуманий британським орігамістом Джоном Смітом, і який обмежений використанням тільки складок горою і долиною. Метою орігамі є полегшення занять недосвідченим орігамістам, а також людям з обмеженими руховими навичками.

Мокре складання

Мокре складання - техніка складання, розроблена Йосі зава Акіра і використовує змочений водою папір для надання фігуркам плавності ліній, виразності, а також жорсткості. Особливо актуальний цей метод для таких негеометричних об'єктів, як фігурки тварин і квітів - в цьому випадку вони виглядають набагато природніше і ближче до оригіналу. Не всякий папір підходить для мокрого складання, а лише той, в який при виробництві додають водорозчинний клей для скріплення волокон. Як правило, даною властивістю володіють щільні сорти паперу.

Складання по розгортці

Розгортка - один з видів діаграм орігамі, що представляє собою креслення, на якому зображені всі складки готової моделі. Складання по розгортці складніше складання за традиційною схемою, проте, даний метод дає не просто інформацію, як скласти модель, але і як вона була придумана - справа в тому, що розгортки використовуються при розробці нових моделей орігамі.

 

 

 

 

 

 

 

Розділ  2: Практична орігаметрія.

2.1. А що таке орігаметрія?

Орігамі - мистецтво складання фігур з паперу без застосування ножиць.

Геометрія в первісному своєму значенні розумілася як наука про фігурах, про взаємне розташування і розміри їх частин, а також про перетворення фігур.

Геометрична діяльність:

1. навчаємо графічним дій,

 2. навичок конструювання,

3. формуємо метричні подання.

Орігаметрія - це поєднання орігамі і геометрії, яка несе в собі оригінальність іншого підходу до геометричних задач.

В  орігаметрії вважається:

 Роль прямих будуть відігравати краї аркуша і лінії згинів, що утворюються при його згинанні.

Роль точок - вершини кутів листа і точки перетину ліній згинів один з одним або з краями листів.

 Термін «технологія» походить від латинського слова construere, що означає - створення моделі, побудова, приведення в певний порядок і взаємовідносини різних окремих предметів, частин, елементів. Вибір саме моделювання з орігамі визначається доступністю для використання на уроці і вдома.

2.2 Знайомство з геометричними поняттями.

У процесі вивчення простих моделей ми знайомимося з дуже потрібними поняттями. Нижче в таблиці перераховані теми і основні геометричні поняття, які ми вивчаємо із застосуванням орігамі.

Тема	Основні геометричні поняття
Види ліній	Пряма, крива, похила, вертикальна, горизонтальна
Пряма лінія і її властивості.	Паралельні і перпендикулярні лінії, що перетинаються
Поняття кута.	Вершина, сторони кута
Бісектриса кута.	Бісектриса
Види кутів.	Прямий, тупий, гострий кут
Суміжні кути.	Суміжні кути.
Розгорнутий кут.	Розгорнутий кут.
Трикутник. Його елементи. Висота трикутника.	Основа, бічна сторона Висота
Види трикутників по кутах.	Прямокутний, гострокутний, тупокутний
Види трикутників по сторонах.	Різносторонній, рівносторонній, рівнобедрений
Квадрат. Прямокутник.	Протилежні сторони, суміжні сторони
Діагоналі багатокутника.	Діагональ
Периметр прямокутника	Периметр

 

2.3. Орігаметричні завдання.

Складання орігамі допомагає вирішувати завдання на теми: поділ відрізка, розподіл кута. Таким чином, за допомогою орігамі вирішуються геометричні задачі на площині, значить це ще одна з точок дотику орігамі з математикою.

Наприклад:

Задача №1: Поділ  прямого кута (Рис.14):

  Відкладання кута в 30 або 60 градусів не представляє проблем. Для цього спочатку розділимо квадрат вертикальної складкою на два рівних прямо-кутника. Потім проведемо складку, яка переносить кут квадрата на зазначену лінію.

 

                    Рис.14

       Кут в 15 градусів тепер можна отримати, ділячи отримані кути в 60 і 30 градусів навпіл.

Задача №2: Поділ аркуша паперу на рівні частини.

    Поділ аркуша паперу на дві частини не представляє складності, оскільки реалізується просто складанням базової форми книжка (Рис.15):

Рис.15

      Наступна задача - розподіл сторони квадрата на чотири рівні частини. Для цього достатньо їх поділити навпіл, а потім, кожну з половинок знову навпіл. Саме так відбувається, коли ми складаємо базову форму двері.

    Перейдемо до більш складної задачі ділення квадратного листа на три частини.

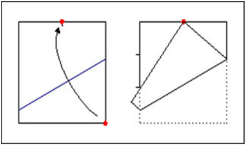     Це завдання вже не настільки проста. Складемо кут квадрата до середини протилежної сторони. В такому випадку точка перетину іншої сторони, протилежної цьому куту і сторони, що прилягає до нього, ділить сторону в співвідношенні  один до двох. (Рис.16) Таким чином, за допомогою тільки складок ми знайшли третину сторони квадрата.

                          Рис.16

Задача №3: Способи виготовлення правильних многокутників із квадрата

(Рис.17-19):                     

 

 

 

 

 

 Рис. 17

Правильний п’ятикутник:

 

 

 

 

 

          Рис.18

 

Правильний восьмикутник:

                              

 

 

 

 

 

 

 

                                         Рис.19

2.4. Модульні орігамі.

Прямокутники, квадрати

Ми згинаємо багато раз.

Виходять фігури

Вони радують нас.

Продовжуючи дослідження, складаючи модульні конструкції, я прийшов до висновку, що вони нагадують геометричні тіла. Складання многогранників – захоплююче заняття, але разом з тим і не просте. Воно вимагає акуратності, точності і високої концентрації уваги. В старших класах на уроках геометрії ми будемо склеювати об'ємні фігури: тетраедри, куби (Рис.20-21) та інші складні многогранники за розкладками, з'єднуючи їх фрагменти клеєм. Неоціненну допомогу у виготовленні многогранників може принести орігамі. Можна виготовити многогранник будь-якого розміру без всякої розкладки. Потрібно тільки вибрати розмір аркуша паперу. Крім того орігамний многогранник завжди можна розібрати, а його модулі при цьому не займуть багато місця.

 

Рис.20                                            Рис.21

 

 

Таким чином, за допомогою орігамі вирішуються геометричні задачі в просторі, значить це ще одна з точок дотику орігамі з математикою.

2.5. Технологічний етап та математичні розрахунки

 Японське прислів'я говорить:

Розкажи мені - я почую,

       Покажи мені - я запам'ятаю,

     Дай мені зробити самому -

                                                 Я зрозумію!"…

 

Моя  робота розпочалася з вибору фігур, які я буду робити. Спочатку планував зробити лебедя. Купив кольоровий двосторонній папір та папір білого кольору.

Якщо довгу і коротку сторону формату А4 розділити на 4 рівні частини і розрізати по намічених лініях, то вийде 16 прямокутників,  приблизно 53× 74 мм.

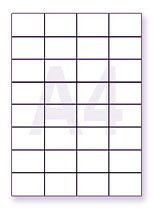
Якщо довгу сторону формату А4 розділити на 8 частин, а коротку на 4 частини, то вийде 32 прямокутника 37 × 53 мм. Залежно  від того на скільки частин ми розділимо лист А4, трикутні модулі матимуть різні розміри. Я вирішив, зробити лебедя з великих модулів. (Великими ми називаємо модулі, якщо лист А4 розділений на 16 прямокутників.) Приступаємо до виготовлення модулів.

Як скласти трикутний модуль орігамі?

1.Поклади прямокутник задньою частиною догори. Зігни навпіл.

 

 

 

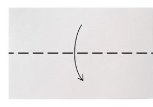
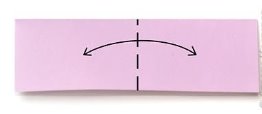
2. Зігніть і розігніть, щоб намітити лінію середини.

3. Зігніть краї до середини. (Як літачок).

              

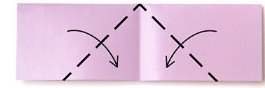
4.Переверни.

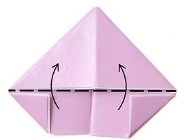5.Загни куточки. (Зверни увагу: між складеним куточком і верхнім трикутником краще залишати невеликий зазор).

 

 

 

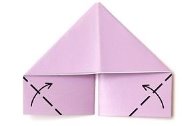
6.Підніми краї вгору.

7.Слади трикутник.

 

 

 

 

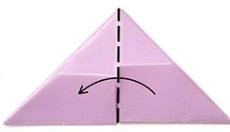
8. Одержаний модуль має два куточка і дві кишеньки.

9.Модулі вставляють один в одного, збираючи ряд за рядом.

 

 

 

 

 

Математичні розрахунки

На виготовлення лебедя (біло-зеленого) потрібно:

• 190 білих модулів
• 110 зелених модулів.

Оскільки з одного листа отримується 16 модулів, то мені потрібно 190/16=11(ост.14), тобто 12 аркушів білого паперу, та  110/16=6(ост.14),

тобто 7 аркушів зеленого паперу.

Розмір листа А4	210*297 мм	S =62370 мм2
Розмір одного прямокутника	52,5*74,25 мм	S = 3898,125 мм2
Ккількість білих модулів	190 шт	S =740643,75мм2
Ккількість зелених модулів	110 шт	S=428793,75мм2
Всього	300 шт	S=1169437,5 мм2

Крім того, я вирахував приблизну площу поверхні мого лебедя. Я розбив поверхню на фігури, площу яких можна обчислити. Розгортка тулуба являє собою прямокутник, площа якого обчислюється за формулою:  S= a ∙ b , де  a= 23см, b=7см.

    S= 23 ∙ 7=161(см²)

 

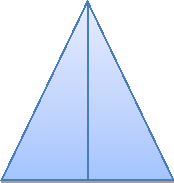Хвіст лебедя та грудка - це  трикутники. Формулу площі трикутника я знайшов в довіднику. Також дізнався, що таке висота трикутника і що є основою трикутника.

S=  ,  

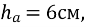1.   a=8см.
2. S=6∙8=24(см²)-грудка

2)  a=9см.

S=6,5∙9=15,75(см²)-хвіст

3)Дзьоб – прямокутний рівнобедрений трикутник, площу якого обчислюємо за формулою: S= , де  .

S=(см²)

Шия являє собою прямокутний паралелепіпед зі сторонами:

а=7см, b= 2см, c= 0,3см. 

S= 2ab+2ac+2bc=2(ab+ac+ bc).

S= 2(7×2+7×0,3+2×0,3)=33,4(см²), отже площа поверхні всього лебедя

 S= 24+15,75+2+33,4=75,15(см²).                                                                                                                                                                                  

2.6. Головоломки та орігамі.

Форма, объём, изгиб, или складка,
И что белый лист без движенья - загадка…

Число уложений и упаковок
Вводит нас в мир головоломок.

И радует магия дивных творений.
Мир оригами, чудо свершений!

За допомогою орігамі можна зробити математичні головоломки, значить - це ще одна з точок дотику орігамі з математикою.

Завдання №1: З даних деталей зібрати куб (Рис.22):

                                                          Рис.22

 

Завдання №2: Зібрати восьмикутник (Рис.23):

 Рис.23

Завдання №3: Зібрати зірку (Рис.24):

Рис.24

2.7.Орігамі в математиці

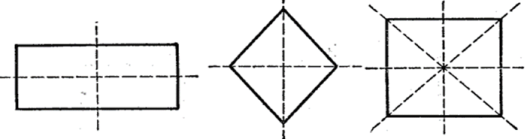
    Орігамі можна використовувати на заняттях з математики в таких завданнях, як: знайти горизонтальні, вертикальні, похилі лінії; знайти всі квадрати; знайти всі трикутники; складання квадрата, суміжні сторони, діагональ.

    Якщо розгорнути фігурку орігамі і подивитися на складки - можна побачити велику кількість багатокутників, з'єднаних один з одним. Працювати можна як по лініях згину виробу, так і в процесі його складання.

    Нижче наведені приклади завдань з вивчення геометрії в процесі складання моделі орігамі.

Завдання 1. Тема «Рівнобедрений трикутник».

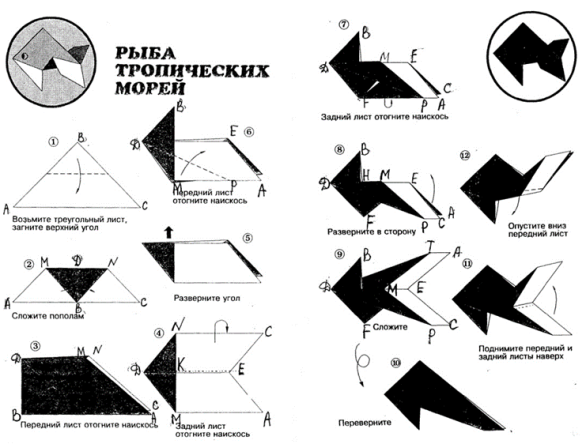
Складіть за запропонованою схемою тропічну рибку. В процесі роботи постарайтеся відповісти на наступні питання:

 1. Яким трикутником є аркуш паперу, з якого складають рибку?

2. Визначте величини всіх кутів цього трикутника.

3. Скільки трикутників ви отримали на малюнку 2 схеми? Визначте вид цих трикутників.

4. На малюнку 4 схеми вкажіть трикутник. Скільки їх на цьому етапі складання фігурки. Визначте кути цих трикутників.

5. На малюнку 5 схеми складання визначте вид трикутника DMP.

6. На малюнку 8 схеми складання моделі назвіть всі трикутники. Визначте їх вид.

Завдання 2. Тема «Кути»

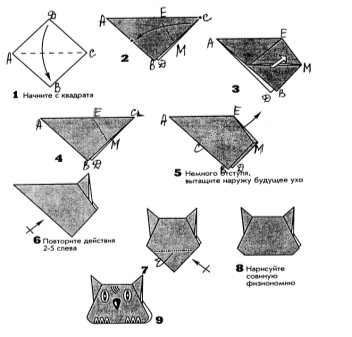
Склади фігурку сови:

1. Складіть базову форму - трикутник (рис.1 схеми складання моделі). Назвіть всі кути на цьому малюнку. Вкажіть їх вершину і сторони.

2. Які кути у вас вийшли на малюнку 2?

3. Чим є АС для кутів ДАВ і ВСД? Чому?

4. Чи рівні кути ЄАД і ЄСМ?

5. На малюнку 2 знайдіть всі суміжні кути.

6. На малюнку 3 скільки кутів вийшло? Які з них тупі кути?

7. На малюнку 5 знайдіть розгорнутий кут і суміжні кути.

8. Які кути на малюнку 5 є тупими?

Намалюйте на отриманої моделі фізіономію сови і іграшка готова.

9. Які кути ви бачите на готової моделі? Позначте їх.

      Фігури в орігамі виконуються з геометричних фігур, значить це ще одна з точок дотику орігамі з математикою. В орігамі фігури можна побудувати без креслярських інструментів, використовуючи кілька згинів.

       При роботі з прямокутником і квадратом знайомимося з поняттями: кут, сторона, діагональ, центр, середня лінія, вершина, поділ відрізка на частини, кута на частини, зі способами складання прямокутника і складання з прямокутника інших геометричних фігур. Таким чином, за допомогою орігамі вирішуються геометричні задачі на площині.

2.8. Орігамі в нашому житті.
Сьогодні мистецтво орігамі переживає черговий пік популярності у всьому світі, до того ж відкриті нові напрямки орігамі та області його застосування. Так, математики використовують основи і принципи цього мистецтва для вирішення геометричних завдань, а архітектори і будівельники побачили в орігамному конструюванні можливості для створення багатогранних структур з плоского листа. Для психологів орігамі - це один з напрямків арт-терапії, так як орігамі в змозі впливати на емоційну сферу людини.

А ось деякі приклади застосування орігамі.

Орігамі – дім

 

 

 

Меблі - орігамі

 

 

 

 

Орігамі - одяг

                                                             

Висновок

У процесі створення проекту я дізнався історію виникнення орігамі, розглянув взаємозв'язок орігамі з математикою.

     Орігамі - і дитяча забава, і елемент дизайну, і невід'ємний атрибут народних свят у багатьох країнах світу. Але ще орігамі сприяє успішному вивченню геометрії. У процесі складання фігур орігамі я знайомився з різними геометричними фігурами; вчився легко орієнтуватися в просторі і на аркуші паперу; знаходити вертикаль, горизонталь, діагональ; орігамі допомагає розвитку перших креслярських навичок, дізнався багато іншого, що відноситься до геометрії і математики. Крім того, орігамі розвиває пам'ять, мислення, просторову уяву, кмітливість.

       Для мене орігамі продовжує залишатися захопленням, яке змогло занурити  з головою в цей дивовижний світ! За допомогою орігамі є можливість показати, що математика не суха наука, а краса і гармонія.

      Мистецтво орігамі тісно пов'язане з математикою і може стати хорошою основою для її вивчення. Займаючись орігамі, я знайшов кілька точок дотику мистецтва орігамі та математики.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ

1. Жукова І.В. Орігамі. Фігурки тварин. – Донецьк: «Видавництво СКІФ», 2011. – 64с.:іл.
2. Игрушки из бумаги. Афонькин С.Ю, Афонькина Е.Ю, - СПб.: Литера, 200г., 192с
3. Carlessi M.A. Origami a moduli triangolari / Maria Angela Carlessi.- Milano:Il Castello Collane Tecniche srl, 2013. – 128 p. (переклад з італійської Юлії Григоренко).
4. «Конструктор оригами. Многогранники.» (метод пособие) Белим С.Н. Омск , 2003 г., 72 с.
5. Орігамі. Прикраси для оселі (пер. з угор. Е.О. Шатілової). – Х.: Віват,2015. – 24 с.: іл. – (Орігамі для всіх).
6. «Оригами. Орнаменты, кусудамы, многогранники». Весновская О.В. Чебоксары, 2003 г., 48 с
7. Планета орігамі. Набір для творчості. – Х.: Ранок, 2014.
8. Энциклопедия для детей. Т.11. Математика / Глав. ред. Э68 М. Д. Аксенова.- М.: Аванта+,1999.- 688с.:ил. , с. 338-341

Ресурси інтернета:

1. http://ru.wikipedia.org/wiki/%D0%9E%D1%80%D0%B8%D0%B3%D0%B0%D0%BC%D0%B8
2. http://ru.wikipedia.org/wiki/%D0%9C%D0%B8%D1%83%D1%80%D0%B0-%D0%BE%D1%80%D0%B8 (Миура-ори)
3. http://origami.ru. Оригами из бумаги.
4. https://sites.google.com/site/school1wiz/uslovnye-oboznacenia Школа волшебников. Условные обозначения
5. http://samorobku.in.ua/origami/bazovi-formi-origami/ Базові форми орігамі
6. http://paper-life.ru/uk/basic-form Базові форми орігамі
7. http://emin197models.ru/ishodnye-formy-origami-master-klass Исходные формы оригами. Мастер-класс