Перетворення енергії під час коливальних рухів
План-конспект уроку фізики _________
в 10 класі
Тема. Перетворення енергії під час коливальних рухів
Мета уроку:
навчальна - сформувати в учнів уміння застосовувати закон збереження енергії для обчислення повної механічної енергії коливного тіла
розвивальна – формувати в учнів вміння користуватися науково-популярною літературою та виявлення творчих здібностей при розв’язуваннні вправ;
виховна – виховати трудолюбивість, точність і чіткість при відповідях і розв’язуванні завдань та навчити дітей «бачити» фізику навколо себе
Тип уроку: вивчення нового матеріалу
План уроку
|
Демонстрації |
5 хв |
|
|
Вивчення нового матеріалу |
ЗО хв |
|
|
Закріплення вивченого матеріалу |
10 хв |
|
Хід уроку
ІІ. Мотивація пізнавальної діяльності
ІІІ. Вивчення нового матеріалу
Як відомо, якщо тертям можна знехтувати, механічна енергія замкнутої системи зберігається. Розглянемо, як змінюються потенціальна й кінетична енергії коливальної системи, на прикладі коливань вантажу, підвішеного на нитці. Якщо вивести систему з положення стійкої рівноваги, то її потенціальна енергія збільшується. У разі повернення в положення стійкої рівноваги потенціальна енергія зменшується, а кінетична — збільшується. У положенні рівноваги кінетична енергія системи є максимальною.
Отже,
^ під час коливань відбуваються взаємні періодичні перетворення потенційної та кінетичної енергій.
Це розповсюджується і на дію пружинного маятника, якщо масою пружини можна знехтувати в порівнянні з масою вантажу.
Періодично повторювані переходи енергії з одного виду в інший
і назад, що супроводжують коливання маятників, характерні для будь-яких коливань узагалі і є такою ж їх характерною ознакою, як наявність положення стійкої рівноваги, інертність і мале тертя.
Покажемо на прикладі коливань вантажу на пружині, що енергія коливальної системи пропорційна квадрату амплітуди коливань. Дійсно, повна енергія системи дорівнює потенційній енергії при максимальному відхиленні від положення рівноваги, тому що кінетична енергія при цьому дорівнює нулю. Потенціальна ж енергія при максимальному відхиленні від положення рівноваги . Розрахунки показують, що енергія коливальної системи пропорційна квадрату амплітуди коливань для будь-яких гармонічних коливань. 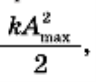
Які максимальні значення швидкості та прискорення під час коливань? Відповісти на це запитання також допоможе закон збереження енергії. Розглянемо коливання вантажу на пружині. Коли система проходить положення рівноваги, її потенціальна енергія
дорівнює нулю, а кінетична — максимальна и дорівнює 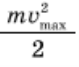
Відповідно до закону збереження енергії, кінетична енергія під час проходження системою положення рівноваги дорівнює її потенційній енергії за максимального відхилення від положення рівноваги, тобто ![]() ,звідси маємо
,звідси маємо
![]()
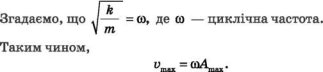
Покажемо, що точно таке співвідношення пов’язує максимальне значення прискорення з максимальним значенням швидкості. Для гармонічних коливань справедливим є рівняння ах = -со2х, звідки отримуємо: ах = со2А^. З урахуванням того, що юА^ = итах, маємо: а = соі>
тах шах
У будь-якій реальній коливальній системі наявне тертя, хоча в багатьох випадках його роль незначна. Наприклад, важкий важок, підвішений на досить довгій нитці, може здійснювати малі коливання впродовж багатьох годин.
^ Коливання, амплітуда яких з плином часу не змінюється, називають незатухаючими.
Якщо ж сили тертя можна зрівняти із силами пружності й тяжіння, що діють у системі, то механічна енергія системи з плином часу помітно зменшуватиметься. Оскільки механічна енергія пропорційна квадрату амплітуди, то в разі зменшення енергії зменшуватиметься й амплітуда коливань. У такому випадку говорять, що коливання затухають.
^ Коливання, амплітуда яких з плином часу зменшується, називають затухаючими.
Графік затухаючих коливань показано на рисунку.
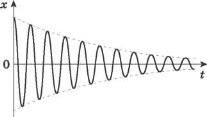
Сили тертя (або опору в рідинах чи газах) можуть бути настільки значними, що коливання навіть не виникнуть. Наприклад, якщо підвішений на нитці важок занурити в грузлу рідину, то після відхилення від положення рівноваги він плавно повернеться в це положення й зупиниться.
Тіло або систему тіл можна «примусити» здійснювати коливання, прикладаючи зовнішню періодичну силу. Скажімо, гойдалку можна розгойдувати, періодично підштовхуючи її.
^ Коливання, що відбуваються під дією зовнішніх сил, які періодично змінюються, називають вимушеними.
Частота вільних коливань визначається характеристиками системи. Ця частота називається власного частотою й зазвичай позначається у0.
Наприклад, для пружинного маятника 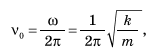
тобто власна частота у0 визначається жорсткістю пружини й масою вантажу.
Для математичного маятника  — , тобто власна
— , тобто власна
частота У0 визначається прискоренням вільного падіння й довжиною маятника.
^ Частота вимушених коливань будь-якої коливальної системи завжди дорівнює частоті зовнішньої сили.
Амплітуда вимушених коливань не зменшується з часом, навіть якщо в системі наявне тертя, тому що втрати механічної енергії, зумовлені тертям, заповнюються за рахунок роботи зовнішніх сил.
Вимушені коливання широко застосовуються в різних вібраційних машинах, за допомогою яких ущільнюють ґрунт і бетон, забивають палі у твердий ґрунт, бурять гірські породи, прокладають водопровідні труби під землею.
Розгойдуючи гойдалку, бажано штовхати її в такт з її власного частотою: у такому випадку розгойдування буде найбільш ефективним. Цей факт указує на те, що амплітуда вимушених коливань істотно залежить від частоти зовнішньої сили. Досліди показують, що амплітуда вимушених коливань тим більша, чим ближчою є частота зовнішньої сили до власної частоти коливань.
^ Явище різкого зростання амплітуди вимушених коливань унаслідок збігу частоти зовнішньої сили з власною частотою системи називається резонансом.
У випадку резонансу напряму зовнішньої сили збігається з напрямом руху, тому вподовж кожного коливання зовнішня сила виконує позитивну роботу. Саме ця «узгодженість» і зумовлює резонанс. Якщо ж частота зовнішньої сили відрізняється від власної частоти системи, зовнішня сила спрямовуватиметься то в напрямі руху, то проти нього. У результаті дія зовнішньої сили буде значно менш ефективною.
^ Графік залежності амплітуди вимушених коливань від частоти зміни зовнішньої сили називають резонансною кривою.
На рисунку побудовано графік залежності амплітуди коливань А від частоти V зовнішньої сили, що змінюється періодично, за умови різних сил тертя в коливальній системі, власна частота коливань якої дорівнює у0.
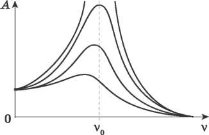
Проаналізувавши графік можна зробити два висновки:
- найбільша амплітуда коливань під дією зовнішньої сили досягається тоді, коли частота зміни зовнішньої сили збігається з частотою вільних коливань;
- чим більша в системі сила тертя, тим меншим є пік резонансної кривої, тобто слабіше виражений резонанс.
Явище резонансу використовується в музичних інструментах для посилення звуку. Резонанс застосовується в багатьох приладах, у тому числі й вимірювальних. Його часто використовують також, коли потрібно зрушити з місця що-небудь важке, наприклад, застряглий автомобіль. У такому випадку добирають частоту поштовхів так, щоб вона збіглася із власного частотою системи, у результаті амплітуда коливань зростає й урешті-решт стає настільки великою, що тіло вже не повертається в попередній стан.
Трапляється, що резонанс призводить навіть до руйнування будинків і мостів. Небезпечним є резонанс і під час роботи будь- яких машин, у яких є частини, що обертаються або рухаються періодично (а такі частини є практично в усіх машинах). Наприклад, « розбалансування » вала верстата або двигуна проявляється в тому, що під час обертання вала виникає періодична сила, що діє на основу механізму, а через неї — на будівлю. Якщо частота цієї сили виявиться близькою до власної частоти будівлі, амплітуда коливань будівлі може зрости настільки, що це призведе до руйнувань.
Щоб уникнути небажаних проявів резонансу, діють двома способами:
- «розузгоджують» частоти, збіг яких може призвести до резонансу. Для цього змінюють або частоту зовнішньої сили, або власну частоту системи;
- збільшують затухання коливань, наприклад, ставлять двигун на гумову підкладку або на пружини.
Запитання до учнів під час викладу нового матеріалу
- Що таке механічна енергія?
- Що таке потенціальна й кінетична енергії?
- У яких точках траєкторії коливне тіло має лише кінетичну енергію?
- У які моменти руху коливне тіло має лише потенційну енергію?
- З якої причини затухають коливання?
- Наведіть приклади вимушених коливань.
- Наведіть приклади корисного використання резонансу.
- У яких випадках необхідно уникати резонансу?
IV.ЗАКРІПЛЕННЯ ВИВЧЕНОГО МАТЕРІАЛУ
- Тренуємося розв'язувати задачі
- У скільки разів потрібно збільшити амплітуду коливань, щоб енергія коливальної системи збільшилася в 9 разів?
-
Пружинний маятник здійснює гармонічні коливання з амплітудою 0,04 м. Якщо зсув — 0,03 м, сила пружності дорівнює
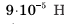 Обчисліть потенційну й кінетичну енергії, що відповідають цьому зсуву, і повну енергію маятника.
Обчисліть потенційну й кінетичну енергії, що відповідають цьому зсуву, і повну енергію маятника.
- Маленька кулька підвішена на нитці завдовжки 1 м до стелі вагона. За якої швидкості вагона кулька особливо сильно коливатиметься під дією ударів коліс об стики рейок? Довжина рейки — 12,5 м. (Відповідь: 6,23 м/с).
- У вагоні потяга підвісили маятник завдовжки 1 м. Під час руху потяга маятник розгойдується від поштовхів на стиках рейок. За якої швидкості потяга маятник розгойдуватиметься особливо сильно, якщо довжина рейок — 25 м?
- Що відбувається з повною механічною енергією коливного тіла за відсутності тертя?
- Що відбувається з повною механічною енергією коливного тіла за наявності тертя?
- Де можна використати явище резонансу?
- Чому в результаті певної швидкості руху вікна автобуса починають сильно деренчати?
- Якщо нести цебра з водою, то при певній швидкості руху вода починає вихлюпуватися. Що необхідно зробити, щоб вихлюпування води припинилося?
- Під час коливань відбуваються взаємні періодичні перетворення потенційної та кінетичної енергій.
- Енергія коливальної системи пропорційна квадрату амплітуди коливань.
-
Швидкість і прискорення під час коливань:
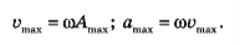
- Коливання, що відбуваються під дією зовнішніх сил, які періодично змінюються, називають вимушеними.
- Частота вимушених коливань будь-якої коливальної системи завжди дорівнює частоті зовнішньої сили.
- Явище різкого зростання амплітуди вимушених коливань унаслідок збігу частоти зовнішньої сили з власного частотою системи називається резонансом.
- Графік залежності амплітуди вимушених коливань від частоти зміни зовнішньої сили називають резонансною кривою.
П.:§43., вик впр №
1


про публікацію авторської розробки
Додати розробку
